Нейронная сеть: архитектура, компоненты и лучшие алгоритмы

Искусственные нейронные сети (ИНС) составляют неотъемлемую часть процесса глубокого обучения. Они вдохновлены неврологической структурой человеческого мозга. Согласно AILabPage , ИНС представляют собой «сложный компьютерный код, написанный с рядом простых, сильно взаимосвязанных элементов обработки, которые вдохновлены биологической структурой мозга человека для моделирования моделей работы и обработки данных (информации) человеческого мозга».

Присоединяйтесь к лучшим онлайн-сертификатам по машинному обучению от ведущих университетов мира — магистерским программам, программам последипломного образования для руководителей и программам расширенных сертификатов в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.

Глубокое обучение фокусируется на пяти основных нейронных сетях, в том числе:

• Многослойный персептрон
• Радиальная базовая сеть
• Рекуррентные нейронные сети
• Генеративно-состязательные сети
• Сверточные нейронные сети.

Нейронная сеть: архитектура

Нейронные сети — это сложные структуры, состоящие из искусственных нейронов, которые могут принимать несколько входных данных для получения одного результата. Это основная задача нейронной сети — преобразовывать входные данные в осмысленные выходные данные. Обычно нейронная сеть состоит из входного и выходного слоев с одним или несколькими скрытыми слоями внутри.

В нейронной сети все нейроны влияют друг на друга, и, следовательно, все они связаны. Сеть может подтверждать и отслеживать каждый аспект набора данных, а также то, как различные части данных могут или не могут быть связаны друг с другом. Именно так нейронные сети способны находить чрезвычайно сложные закономерности в огромных объемах данных.

Читайте: Машинное обучение против нейронных сетей

В нейронной сети поток информации происходит двумя способами:

• Сети с прямой связью: в этой модели сигналы проходят только в одном направлении, к выходному слою. Сети прямого распространения имеют входной слой и один выходной слой с нулевым или несколькими скрытыми слоями. Они широко используются в распознавании образов.
• Сети обратной связи: в этой модели рекуррентные или интерактивные сети используют свое внутреннее состояние (память) для обработки последовательности входных данных. В них сигналы могут проходить в обоих направлениях через петли (скрытые слои) в сети. Они обычно используются во временных рядах и последовательных задачах.

Нейронная сеть: компоненты

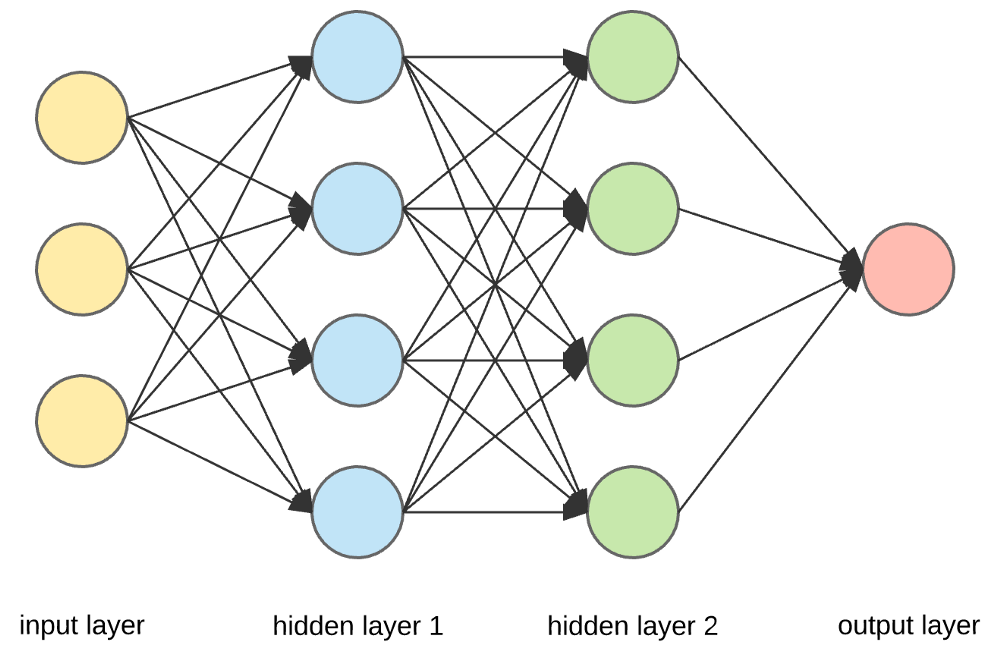
Источник

Входные слои, нейроны и веса –

На приведенном выше рисунке крайний желтый слой — это входной слой. Нейрон является базовой единицей нейронной сети. Они получают входные данные от внешнего источника или других узлов. Каждый узел связан с другим узлом следующего слоя, и каждое такое соединение имеет определенный вес. Веса присваиваются нейрону на основе его относительной важности по сравнению с другими входными данными.

Когда все значения узлов из желтого слоя перемножаются (вместе с их весом) и суммируются, создается значение для первого скрытого слоя. Основываясь на суммированном значении, синий слой имеет предопределенную функцию «активации», которая определяет, будет ли этот узел «активирован» и насколько он будет «активен».

Давайте разберемся в этом, используя простую повседневную задачу – заваривание чая. В процессе приготовления чая ингредиенты, используемые для приготовления чая (вода, чайные листья, молоко, сахар и специи), являются «нейронами», поскольку они составляют отправную точку процесса. Количество каждого ингредиента представляет собой «вес». Как только вы положите чайные листья в воду и добавите в кастрюлю сахар, специи и молоко, все ингредиенты смешаются и перейдут в другое состояние. Этот процесс преобразования представляет собой «функцию активации».

Узнайте о: Глубокое обучение против нейронных сетей

Скрытые слои и выходной слой –

Слой или слои, скрытые между входным и выходным слоями, называются скрытыми слоями. Он называется скрытым слоем, так как всегда скрыт от внешнего мира. Основные вычисления нейронной сети происходят в скрытых слоях. Таким образом, скрытый слой получает все входные данные от входного слоя и выполняет необходимые вычисления для получения результата. Затем этот результат пересылается на выходной уровень, чтобы пользователь мог просмотреть результат вычисления.

В нашем примере с приготовлением чая, когда мы смешиваем все ингредиенты, рецептура меняет свое состояние и цвет при нагревании. Ингредиенты представляют собой скрытые слои. Здесь нагревание представляет собой процесс активации, который в конечном итоге приводит к результату – чаю.

Нейронная сеть: алгоритмы

В нейронной сети процесс обучения (или обучения) инициируется путем разделения данных на три разных набора:

• Набор обучающих данных — этот набор данных позволяет нейронной сети понимать веса между узлами.
• Набор данных проверки — этот набор данных используется для точной настройки производительности нейронной сети.
• Тестовый набор данных — этот набор данных используется для определения точности и погрешности нейронной сети.

После того, как данные разделены на эти три части, к ним применяются алгоритмы нейронной сети для обучения нейронной сети. Процедура, используемая для облегчения процесса обучения в нейронной сети, известна как оптимизация, а используемый алгоритм называется оптимизатором. Существуют различные типы алгоритмов оптимизации, каждый со своими уникальными характеристиками и аспектами, такими как требования к памяти, числовая точность и скорость обработки.

Прежде чем мы углубимся в обсуждение различных алгоритмов нейронной сети , давайте сначала разберемся с проблемой обучения.

Читайте также : Применение нейронных сетей в реальном мире.

В чем проблема обучения?

Мы представляем задачу обучения в терминах минимизации индекса потерь ( f ). Здесь « f » — это функция, которая измеряет производительность нейронной сети в заданном наборе данных. Как правило, индекс потерь состоит из члена ошибки и члена регуляризации. В то время как член ошибки оценивает, как нейронная сеть соответствует набору данных, член регуляризации помогает предотвратить проблему переобучения, контролируя эффективную сложность нейронной сети.

Функция потерь [ f (w ] зависит от адаптивных параметров — весов и смещений — нейронной сети, Эти параметры могут быть сгруппированы в один n-мерный вектор весов ( w ).

Вот графическое представление функции потерь:

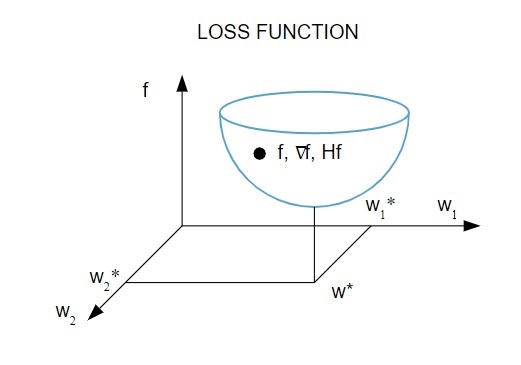
Источник

Согласно этой диаграмме минимум функции потерь приходится на точку ( w* ). В любой момент можно вычислить первую и вторую производные функции потерь. Первые производные группируются в векторе градиента, а его компоненты изображаются как:

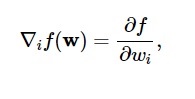
Источник

Здесь i = 1,…..,n .

Вторые производные функции потерь сгруппированы в матрице Гессе , например:

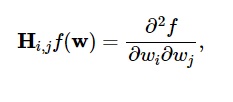
Источник

Здесь i,j = 0,1,…

Теперь, когда мы знаем, в чем проблема обучения, мы можем обсудить пять основных

Алгоритмы нейронной сети .

1. Одномерная оптимизация

Поскольку функция потерь зависит от нескольких параметров, методы одномерной оптимизации играют важную роль в обучении нейронной сети. Алгоритмы обучения сначала вычисляют направление обучения ( d ), а затем вычисляют скорость обучения ( η ), которая помогает минимизировать потери в направлении обучения [ f(η) ].

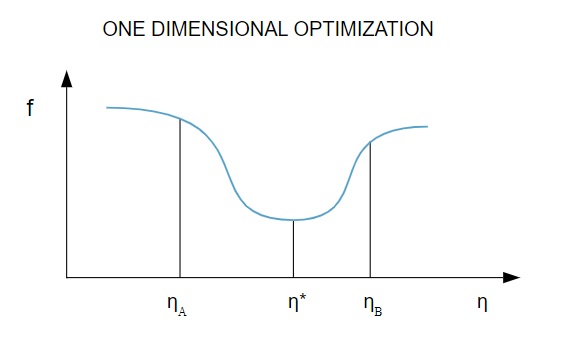
Источник

На диаграмме точки η1 и η2 определяют интервал, содержащий минимум функции f, η* .

Таким образом, методы одномерной оптимизации направлены на поиск минимума заданной одномерной функции. Двумя наиболее часто используемыми одномерными алгоритмами являются метод золотого сечения и метод Брента.

Метод золотого сечения

Алгоритм поиска золотого сечения используется для нахождения минимума или максимума функции одной переменной [ f(x) ]. Если мы уже знаем, что функция имеет минимум между двумя точками, то мы можем выполнить итеративный поиск точно так же, как при поиске пополам корня уравнения f(x) = 0 . Кроме того, если мы можем найти три точки ( x0 < x1 < x2 ), соответствующие f (x0) > f (x1) > f (X2) в окрестности минимума, то мы можем сделать вывод, что минимум существует между x0 и x2 . Чтобы узнать этот минимум, мы можем рассмотреть другую точку x3 между x1 и x2 , что даст нам следующие результаты:

• Если f(x3) = f3a > f(x1), то минимум находится внутри интервала x3 – x0 = a + c , связанного с тремя новыми точками x0 < x1 < x3 (здесь x2 заменяется на x3 ).
• Если f(x3) = f3b > f(x1 ), то минимум находится внутри интервала x2 – x1 = b , связанного с тремя новыми точками x1 < x3 < x2 (здесь x0 заменяется на x1 ).

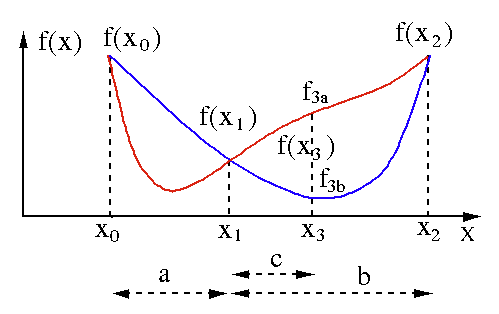
Источник

Метод Брента

Метод Брента представляет собой алгоритм поиска корня, который сочетает в себе скобки корня , деление пополам , секущую и обратную квадратичную интерполяцию . Хотя этот алгоритм пытается использовать метод быстрой сходящейся секущей или обратную квадратичную интерполяцию, когда это возможно, он обычно возвращается к методу деления пополам. Реализованный на языке Wolfram Language , метод Брента выражается следующим образом:

Метод -> Brent в FindRoot [eqn, x, x0, x1].

В методе Брента мы используем интерполирующий многочлен Лагранжа степени 2. В 1973 году Брент заявил, что этот метод всегда будет сходиться, если значения функции вычислимы в пределах определенной области, включая корень. Если есть три точки x1, x2 и x3 , метод Брента соответствует x как квадратичной функции y , используя формулу интерполяции:

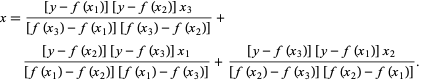
Источник

Последующие оценки корней достигаются путем рассмотрения, в результате чего получается следующее уравнение:

Источник

Здесь P = S [T(R – T) (x3 – x2) – (1 – R) (x2 – x1)] и Q = (T – 1) (R – 1) (S – 1) и,

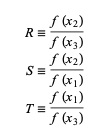
Источник

2. Многомерная оптимизация

К настоящему времени мы уже знаем, что задача обучения нейронных сетей направлена ​​на поиск вектора параметров ( w* ), для которого функция потерь ( f ) принимает минимальное значение. Согласно предписаниям стандартного условия, если нейронная сеть имеет минимум функции потерь, градиент является нулевым вектором.

Поскольку функция потерь является нелинейной функцией параметров, найти замкнутые алгоритмы обучения на минимум невозможно. Однако, если мы рассмотрим поиск в пространстве параметров, который включает в себя ряд шагов, на каждом шаге потери будут уменьшаться за счет настройки параметров нейронной сети.

В многомерной оптимизации нейронная сеть обучается путем выбора случайного вектора параметров, а затем генерации последовательности параметров, чтобы гарантировать, что функция потерь уменьшается с каждой итерацией алгоритма. Это изменение потерь между двумя последующими шагами известно как «уменьшение потерь». Процесс уменьшения потерь продолжается до тех пор, пока алгоритм обучения не достигнет или не удовлетворит заданному условию.

Вот три примера алгоритмов многомерной оптимизации:

Градиентный спуск

Алгоритм градиентного спуска, вероятно, самый простой из всех обучающих алгоритмов. Поскольку он опирается на информацию, полученную из вектора градиента, это метод первого порядка. В этом методе мы возьмем f[w(i)] = f(i) и ∇f[w(i)] = g(i) . Начальной точкой этого обучающего алгоритма является w(0), который продолжает прогрессировать до тех пор, пока указанный критерий не будет удовлетворен – он движется от w(i) к w(i+1) в направлении обучения d(i) = −g(i) . Следовательно, градиентный спуск повторяется следующим образом:

w(i+1) = w(i)−g(i)η(i),

Здесь i = 0,1,…

Параметр η представляет скорость обучения. Вы можете установить фиксированное значение для η или установить его на значение, найденное одномерной оптимизацией по направлению обучения на каждом шаге. Однако предпочтительно устанавливать оптимальное значение скорости обучения, достигаемое путем минимизации линии на каждом шаге.

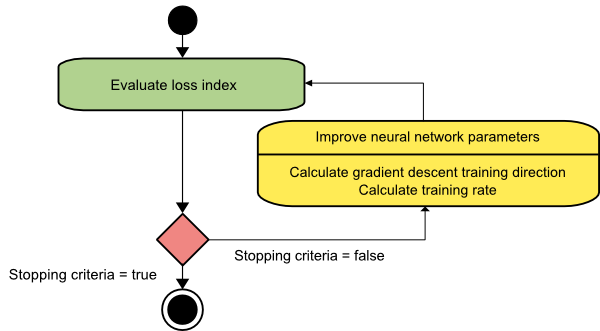
Источник

У этого алгоритма много ограничений, поскольку он требует многочисленных итераций для функций с длинными и узкими структурами долины. Хотя функция потерь быстрее всего убывает в направлении нисходящего градиента, она не всегда обеспечивает самую быструю сходимость.

метод Ньютона

Это алгоритм второго порядка, так как он использует матрицу Гессе. Метод Ньютона направлен на поиск лучших направлений обучения, используя вторые производные функции потерь. Здесь мы будем обозначать f[w(i)] = f(i), ∇f[w(i)]=g(i) и Hf[w(i)] = H(i) . Теперь мы рассмотрим квадратичное приближение f при w(0) с использованием разложения в ряд Тейлора, например:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Здесь H(0) — матрица Гессе функции f , вычисленная в точке w(0) . Рассматривая g = 0 для минимума f(w) , мы получаем следующее уравнение:

г = г (0) + Н (0) ⋅ (ш - ш (0)) = 0

В результате мы видим, что, начиная с вектора параметров w(0), метод Ньютона выполняет следующие итерации:

ш (я + 1) = ш (я) - Н (я) - 1 ⋅ г (я)

Здесь i = 0,1 ,… и вектор H(i)−1⋅g(i) называется «шагом Ньютона». Вы должны помнить, что изменение параметра может двигаться к максимуму, а не к минимуму. Обычно это происходит, если матрица Гессе не является положительно определенной, что приводит к уменьшению оценки функции на каждой итерации. Однако, чтобы избежать этой проблемы, мы обычно модифицируем уравнение метода следующим образом:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Здесь i = 0,1 ,….

Вы можете установить скорость обучения η на фиксированное значение или значение, полученное с помощью минимизации линии. Итак, вектор d(i)=H(i)−1⋅g(i) становится направлением обучения для метода Ньютона.

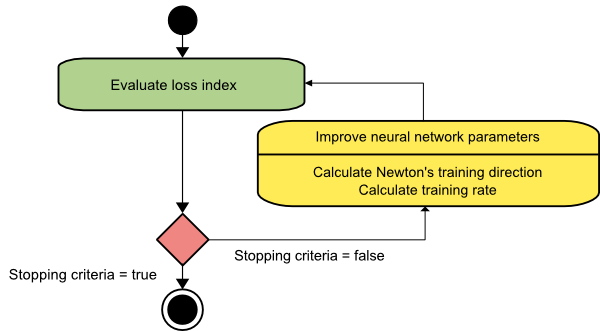
Источник

Основным недостатком метода Ньютона является то, что точная оценка гессиана и его обратного значения требует довольно больших затрат.

Сопряженный градиент

Метод сопряженных градиентов находится между градиентным спуском и методом Ньютона. Это промежуточный алгоритм - хотя он направлен на ускорение фактора медленной сходимости метода градиентного спуска, он также устраняет необходимость в информационных требованиях, касающихся оценки, хранения и обращения матрицы Гессе, обычно требуемых в методе Ньютона.

Алгоритм обучения сопряженному градиенту выполняет поиск в сопряженных направлениях, что обеспечивает более быструю сходимость, чем в направлениях градиентного спуска. Эти направления обучения сопряжены в соответствии с матрицей Гессе. Здесь d обозначает вектор направления обучения. Если мы начнем с начального вектора параметров [w(0)] и начального вектора направления обучения [d(0)=−g(0)] , метод сопряженного градиента генерирует последовательность направлений обучения, представленную как:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Здесь i = 0,1 ,… и γ — сопряженный параметр. Направление обучения для всех алгоритмов сопряженного градиента периодически сбрасывается на отрицательное значение градиента. Параметры улучшаются, а скорость обучения ( η ) достигается за счет минимизации линии в соответствии с выражением, показанным ниже:

ш(я+1) = ш(я)+d(я)⋅η(я)

Здесь i = 0,1 ,…

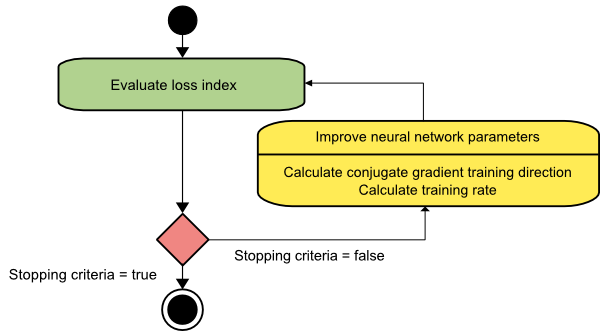
Источник

Заключение

Каждый алгоритм имеет свои уникальные преимущества и недостатки. Это всего лишь несколько алгоритмов, используемых для обучения нейронных сетей, и их функции демонстрируют только верхушку айсберга — по мере развития фреймворков глубокого обучения будут развиваться и функциональные возможности этих алгоритмов.

Если вам интересно узнать больше о нейронных сетях, программах машинного обучения и искусственном интеллекте , ознакомьтесь с программой Executive PG IIIT-B и upGrad по машинному обучению и искусственному интеллекту , которая предназначена для работающих профессионалов и предлагает более 450 часов интенсивного обучения, 30+ тематические исследования и задания, статус выпускника IIIT-B, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.