Rede Neural: Arquitetura, Componentes e Principais Algoritmos

As Redes Neurais Artificiais (RNAs) são parte integrante do processo de Deep Learning. Eles são inspirados na estrutura neurológica do cérebro humano. De acordo com AILabPage , as RNAs são “códigos de computador complexos escritos com o número de elementos de processamento simples e altamente interconectados, inspirados na estrutura biológica do cérebro humano para simular modelos de trabalho e processamento de dados (informações) do cérebro humano”.

Junte -se às melhores certificações de aprendizado de máquina on-line das principais universidades do mundo - mestrados, programas de pós-graduação executiva e programa de certificação avançada em ML e IA para acelerar sua carreira.

O Deep Learning se concentra em cinco redes neurais principais, incluindo:

• Perceptron de várias camadas
• Rede de base radial
• Redes Neurais Recorrentes
• Redes Adversárias Geradoras
• Redes Neurais Convolucionais.

Rede Neural: Arquitetura

Redes neurais são estruturas complexas feitas de neurônios artificiais que podem receber múltiplas entradas para produzir uma única saída. Este é o principal trabalho de uma Rede Neural – transformar a entrada em uma saída significativa. Normalmente, uma Rede Neural consiste em uma camada de entrada e saída com uma ou várias camadas ocultas.

Em uma Rede Neural, todos os neurônios influenciam uns aos outros e, portanto, estão todos conectados. A rede pode reconhecer e observar todos os aspectos do conjunto de dados em mãos e como as diferentes partes dos dados podem ou não se relacionar entre si. É assim que as Redes Neurais são capazes de encontrar padrões extremamente complexos em grandes volumes de dados.

Leia: Aprendizado de máquina versus redes neurais

Em uma Rede Neural, o fluxo de informações ocorre de duas maneiras –

• Redes Feedforward: Neste modelo, os sinais viajam apenas em uma direção, em direção à camada de saída. As redes feedforward têm uma camada de entrada e uma única camada de saída com zero ou várias camadas ocultas. Eles são amplamente utilizados no reconhecimento de padrões.
• Redes de Feedback: Neste modelo, as redes recorrentes ou interativas utilizam seu estado interno (memória) para processar a sequência de entradas. Neles, os sinais podem trafegar em ambas as direções através dos loops (camadas ocultas) na rede. Eles são normalmente usados ​​em séries temporais e tarefas sequenciais.

Rede Neural: Componentes

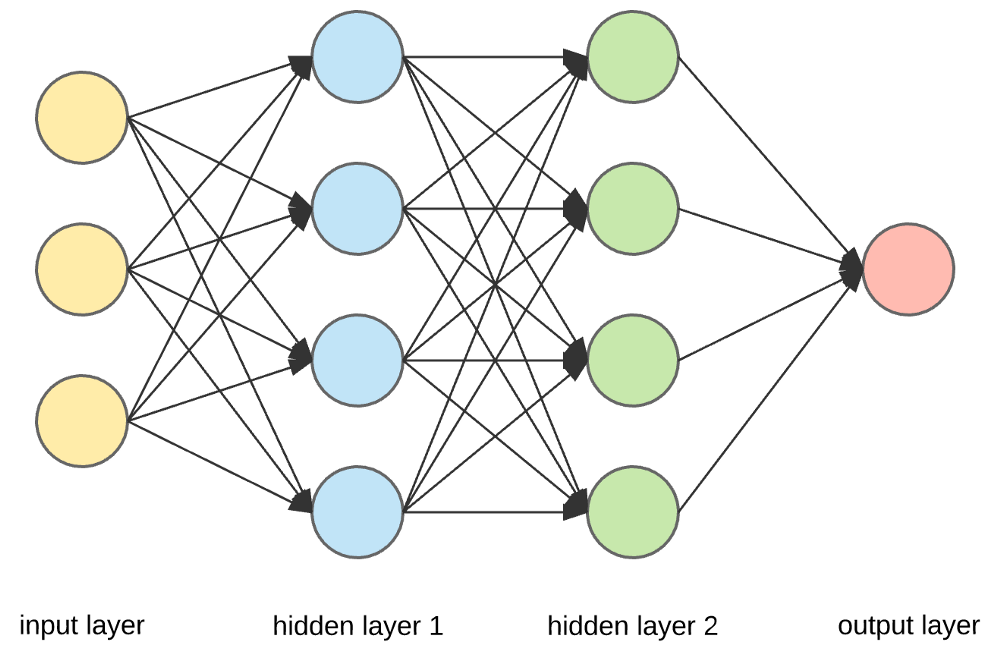
Fonte

Camadas de entrada, neurônios e pesos -

Na imagem acima, a camada amarela mais externa é a camada de entrada. Um neurônio é a unidade básica de uma rede neural. Eles recebem entrada de uma fonte externa ou de outros nós. Cada nó está conectado com outro nó da próxima camada, e cada uma dessas conexões tem um peso específico. Os pesos são atribuídos a um neurônio com base em sua importância relativa em relação a outras entradas.

Quando todos os valores de nós da camada amarela são multiplicados (junto com seu peso) e resumidos, gera-se um valor para a primeira camada oculta. Com base no valor resumido, a camada azul possui uma função de “ativação” pré-definida que determina se este nó será ou não “ativado” e quão “ativo” ele será.

Vamos entender isso usando uma tarefa simples do dia a dia – fazer chá. No processo de fabricação do chá, os ingredientes usados ​​para fazer o chá (água, folhas de chá, leite, açúcar e especiarias) são os “neurônios”, pois são os pontos de partida do processo. A quantidade de cada ingrediente representa o “peso”. Depois de colocar as folhas de chá na água e adicionar o açúcar, as especiarias e o leite na panela, todos os ingredientes se misturam e se transformam em outro estado. Este processo de transformação representa a “função de ativação”.

Saiba mais sobre: ​​Deep Learning vs Redes Neurais

Camadas ocultas e camada de saída -

A camada ou camadas ocultas entre a camada de entrada e saída é conhecida como camada oculta. É chamada de camada oculta, pois está sempre oculta do mundo externo. A computação principal de uma Rede Neural ocorre nas camadas ocultas. Assim, a camada oculta recebe todas as entradas da camada de entrada e realiza o cálculo necessário para gerar um resultado. Este resultado é então encaminhado para a camada de saída para que o usuário possa visualizar o resultado da computação.

Em nosso exemplo de chá, quando misturamos todos os ingredientes, a formulação muda de estado e cor ao ser aquecida. Os ingredientes representam as camadas ocultas. Aqui o aquecimento representa o processo de ativação que finalmente entrega o resultado – chá.

Rede Neural: Algoritmos

Em uma Rede Neural, o processo de aprendizado (ou treinamento) é iniciado dividindo os dados em três conjuntos diferentes:

• Conjunto de dados de treinamento – Este conjunto de dados permite que a Rede Neural entenda os pesos entre os nós.
• Conjunto de dados de validação – Este conjunto de dados é usado para ajustar o desempenho da Rede Neural.
• Conjunto de dados de teste – Este conjunto de dados é usado para determinar a precisão e a margem de erro da Rede Neural.

Uma vez que os dados são segmentados nessas três partes, os algoritmos de Rede Neural são aplicados a eles para treinar a Rede Neural. O procedimento utilizado para facilitar o processo de treinamento em uma Rede Neural é conhecido como otimização, e o algoritmo utilizado é chamado de otimizador. Existem diferentes tipos de algoritmos de otimização, cada um com suas características e aspectos exclusivos, como requisitos de memória, precisão numérica e velocidade de processamento.

Antes de mergulharmos na discussão dos diferentes algoritmos de Rede Neural , vamos entender primeiro o problema de aprendizado.

Leia também : Aplicações de rede neural no mundo real

O que é o Problema de Aprendizagem?

Representamos o problema de aprendizagem em termos da minimização de um índice de perda ( f ). Aqui, “ f ” é a função que mede o desempenho de uma Rede Neural em um determinado conjunto de dados. Geralmente, o índice de perda consiste em um termo de erro e um termo de regularização. Enquanto o termo de erro avalia como uma Rede Neural se ajusta a um conjunto de dados, o termo de regularização ajuda a evitar o problema de overfitting, controlando a complexidade efetiva da Rede Neural.

A função de perda [ f(w ] depende dos parâmetros adaptativos – pesos e bias – da Rede Neural, que podem ser agrupados em um único vetor de peso n-dimensional ( w ).

Aqui está uma representação pictórica da função de perda:

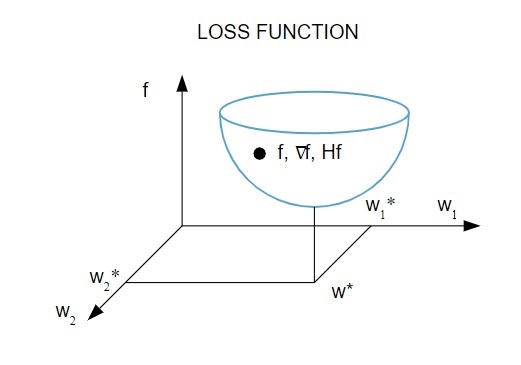
Fonte

De acordo com este diagrama, o mínimo da função de perda ocorre no ponto ( w* ). A qualquer momento, você pode calcular a primeira e a segunda derivada da função de perda. As primeiras derivadas são agrupadas no vetor gradiente e seus componentes são representados como:

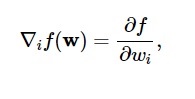
Fonte

Aqui, i = 1,…..,n .

As segundas derivadas da função de perda são agrupadas na matriz Hessiana , assim:

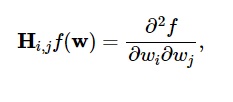
Fonte

Aqui, i,j = 0,1,…

Agora que sabemos qual é o problema de aprendizagem, podemos discutir os cinco principais

Algoritmos de rede neural .

1. Otimização unidimensional

Como a função de perda depende de vários parâmetros, os métodos de otimização unidimensional são fundamentais no treinamento de redes neurais. Os algoritmos de treinamento primeiro calculam uma direção de treinamento ( d ) e então calculam a taxa de treinamento ( η ) que ajuda a minimizar a perda na direção de treinamento [ f(η) ].

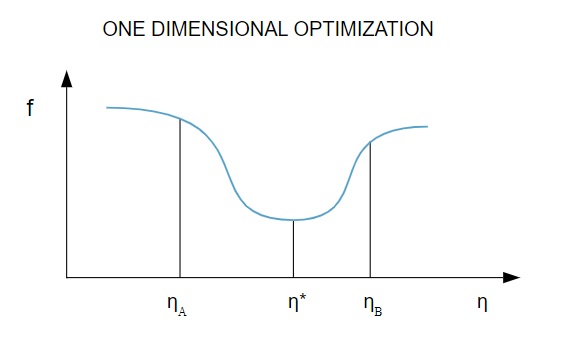
Fonte

No diagrama, os pontos η1 e η2 definem o intervalo que contém o mínimo de f, η* .

Assim, os métodos de otimização unidimensional visam encontrar o mínimo de uma determinada função unidimensional. Dois dos algoritmos unidimensionais mais usados ​​são o Método da Seção Dourada e o Método de Brent.

Método da Seção Dourada

O algoritmo de busca da seção áurea é usado para encontrar o mínimo ou o máximo de uma função de variável única [ f(x) ]. Se já sabemos que uma função tem um mínimo entre dois pontos, podemos realizar uma busca iterativa como faríamos na busca por bissecção pela raiz de uma equação f(x) = 0 . Além disso, se pudermos encontrar três pontos ( x0 < x1 < x2 ) correspondentes a f(x0) > f(x1) > f(X2) na vizinhança do mínimo, então podemos deduzir que existe um mínimo entre x0 e x2 . Para descobrir esse mínimo, podemos considerar outro ponto x3 entre x1 e x2 , que nos dará os seguintes resultados:

• Se f(x3) = f3a > f(x1), o mínimo está dentro do intervalo x3 – x0 = a + c que está relacionado com três novos pontos x0 < x1 < x3 (aqui x2 é substituído por x3 ).
• Se f(x3) = f3b > f(x1 ), o mínimo está dentro do intervalo x2 – x1 = b relacionado com três novos pontos x1 < x3 < x2 (aqui x0 é substituído por x1 ).

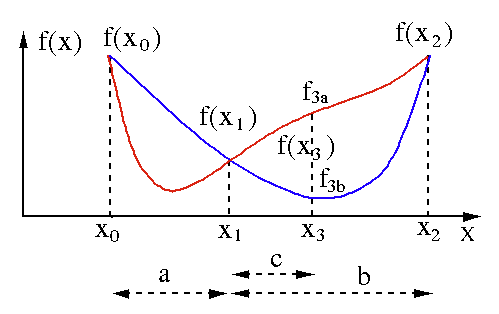
Fonte

Método de Brent

O método de Brent é um algoritmo de descoberta de raízes que combina a interpolação quadrática entre colchetes , bisseção , secante e inversa . Embora este algoritmo tente usar o método secante de convergência rápida ou interpolação quadrática inversa sempre que possível, ele geralmente reverte para o método da bissecção. Implementado na Wolfram Language , o método de Brent é expresso como:

Método -> Brent em FindRoot [eqn, x, x0, x1].

No método de Brent, usamos um polinômio interpolador de Lagrange de grau 2. Em 1973, Brent afirmou que esse método sempre convergirá, desde que os valores da função sejam computáveis ​​dentro de uma região específica, incluindo uma raiz. Se houver três pontos x1, x2 e x3 , o método de Brent ajusta x como uma função quadrática de y , usando a fórmula de interpolação:

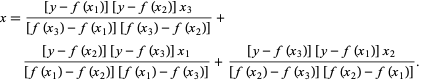
Fonte

As estimativas de raiz subsequentes são alcançadas considerando, produzindo assim a seguinte equação:

Fonte

Aqui, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] e Q = (T – 1) (R – 1) (S – 1) e,

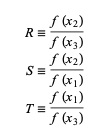
Fonte

2. Otimização multidimensional

A esta altura, já sabemos que o problema de aprendizado para Redes Neurais visa encontrar o vetor de parâmetros ( w* ) para o qual a função de perda ( f ) assume um valor mínimo. De acordo com os mandatos da condição padrão, se a Rede Neural estiver no mínimo da função de perda, o gradiente é o vetor zero.

Como a função de perda é uma função não linear dos parâmetros, é impossível encontrar os algoritmos de treinamento fechados para o mínimo. No entanto, se considerarmos a busca no espaço de parâmetros que inclui uma série de etapas, a cada etapa, a perda será reduzida ajustando os parâmetros da Rede Neural.

Na otimização multidimensional, uma Rede Neural é treinada escolhendo um vetor aleatório de parâmetros e gerando uma sequência de parâmetros para garantir que a função de perda diminua a cada iteração do algoritmo. Essa variação de perda entre duas etapas subsequentes é conhecida como “decremento de perda”. O processo de decremento da perda continua até que o algoritmo de treinamento atinja ou satisfaça a condição especificada.

Aqui estão três exemplos de algoritmos de otimização multidimensional:

Gradiente descendente

O algoritmo de gradiente descendente é provavelmente o mais simples de todos os algoritmos de treinamento. Como ele se baseia nas informações fornecidas pelo vetor gradiente, é um método de primeira ordem. Neste método, tomaremos f[w(i)] = f(i) e ∇f[w(i)] = g(i) . O ponto de partida deste algoritmo de treinamento é w(0) que continua progredindo até que o critério especificado seja satisfeito – ele se move de w(i) para w(i+1) na direção de treinamento d(i) = −g(i) . Assim, o gradiente descendente itera da seguinte forma:

w(i+1) = w(i)−g(i)η(i),

Aqui, i = 0,1,…

O parâmetro η representa a taxa de treinamento. Você pode definir um valor fixo para η ou defini-lo como o valor encontrado pela otimização unidimensional ao longo da direção de treinamento em cada etapa. No entanto, é preferível definir o valor ideal para a taxa de treinamento alcançada pela minimização da linha em cada etapa.

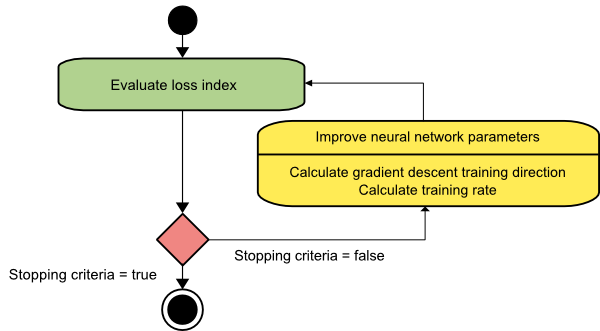
Fonte

Esse algoritmo tem muitas limitações, pois requer inúmeras iterações para funções que possuem estruturas de vale longas e estreitas. Embora a função de perda diminua mais rapidamente na direção do gradiente descendente, ela nem sempre garante a convergência mais rápida.

O método de Newton

Este é um algoritmo de segunda ordem, pois aproveita a matriz Hessiana. O método de Newton visa encontrar melhores direções de treinamento fazendo uso das segundas derivadas da função de perda. Aqui, denotaremos f[w(i)] = f(i), ∇f[w(i)]=g(i) , e Hf[w(i)] = H(i) . Agora, vamos considerar a aproximação quadrática de f em w(0) usando a expansão em série de Taylor, assim:

f = f(0)+g(0)⋅[w−w(0)] + 0,5⋅[w−w(0)]2⋅H(0)

Aqui, H(0) é a matriz hessiana de f calculada no ponto w(0) . Considerando g = 0 para o mínimo de f(w) , obtemos a seguinte equação:

g = g(0)+H(0)⋅(w−w(0))=0

Como resultado, podemos ver que a partir do vetor de parâmetros w(0), o método de Newton itera da seguinte forma:

w(i+1) = w(i)−H(i)−1⋅g(i)

Aqui, i = 0,1 ,… e o vetor H(i)−1⋅g(i) é referido como “Passo de Newton”. Você deve lembrar que a mudança de parâmetro pode se mover para um máximo em vez de ir na direção de um mínimo. Normalmente, isso acontece se a matriz Hessiana não for definida positiva, fazendo com que a avaliação da função seja reduzida a cada iteração. No entanto, para evitar esse problema, geralmente modificamos a equação do método da seguinte maneira:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Aqui, i = 0,1 ,….

Você pode definir a taxa de treinamento η para um valor fixo ou o valor obtido por meio da minimização da linha. Assim, o vetor d(i)=H(i)−1⋅g(i) torna-se a direção de treinamento para o método de Newton.

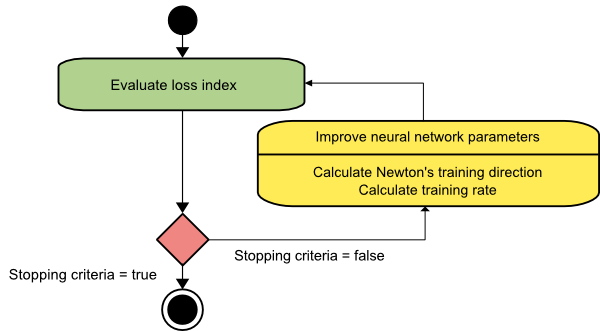
Fonte

A principal desvantagem do método de Newton é que a avaliação exata do Hessiano e seu inverso são cálculos bastante caros.

Gradiente conjugado

O método do gradiente conjugado fica entre o gradiente descendente e o método de Newton. Trata-se de um algoritmo intermediário – ao mesmo tempo em que visa acelerar o fator de convergência lenta do método gradiente descendente, também elimina a necessidade de informações referentes à avaliação, armazenamento e inversão da matriz Hessiana normalmente exigidas no método de Newton.

O algoritmo de treinamento de gradiente conjugado realiza a busca nas direções conjugadas que proporcionam uma convergência mais rápida do que as direções de descida do gradiente. Essas direções de treinamento são conjugadas de acordo com a matriz hessiana. Aqui, d denota o vetor de direção de treinamento. Se começarmos com um vetor de parâmetro inicial [w(0)] e um vetor de direção de treinamento inicial [d(0)=−g(0)] , o método do gradiente conjugado gera uma sequência de direções de treinamento representadas como:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Aqui, i = 0,1 ,… e γ é o parâmetro conjugado. A direção de treinamento para todos os algoritmos de gradiente conjugado é periodicamente redefinida para o negativo do gradiente. Os parâmetros são melhorados, e a taxa de treinamento ( η ) é alcançada via minimização de linhas, conforme a expressão abaixo:

w(i+1) = w(i)+d(i)⋅η(i)

Aqui, i = 0,1 ,…

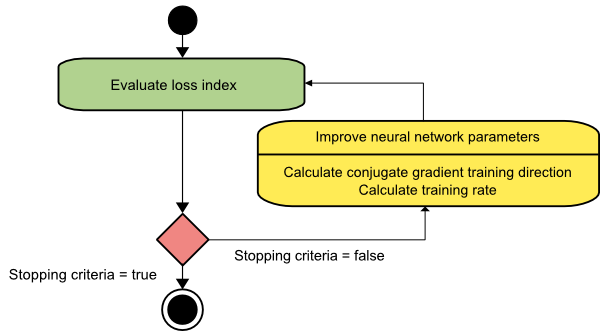
Fonte

Conclusão

Cada algoritmo vem com vantagens e desvantagens únicas. Esses são apenas alguns algoritmos usados ​​para treinar Redes Neurais, e suas funções demonstram apenas a ponta do iceberg – à medida que os frameworks de Deep Learning avançam, as funcionalidades desses algoritmos também.

Se você estiver interessado em saber mais sobre rede neural, programas de aprendizado de máquina e IA , confira o Programa PG Executivo do IIIT-B e do upGrad em aprendizado de máquina e IA , projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, status de ex-alunos do IIIT-B, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.