Réseau de neurones : architecture, composants et principaux algorithmes

Les réseaux de neurones artificiels (ANN) font partie intégrante du processus d'apprentissage en profondeur. Ils s'inspirent de la structure neurologique du cerveau humain. Selon AILabPage , les ANN sont "un code informatique complexe écrit avec le nombre d'éléments de traitement simples et hautement interconnectés qui s'inspire de la structure biologique du cerveau humain pour simuler le travail du cerveau humain et traiter les modèles de données (Information)".

Rejoignez les meilleures certifications d'apprentissage automatique en ligne des meilleures universités du monde - Masters, programmes de troisième cycle pour cadres et programme de certificat avancé en ML et IA pour accélérer votre carrière.

Deep Learning se concentre sur cinq réseaux de neurones principaux, notamment :

• Perceptron multicouche
• Réseau à base radiale
• Réseaux de neurones récurrents
• Réseaux antagonistes génératifs
• Réseaux de neurones convolutifs.

Réseau de neurones : architecture

Les réseaux de neurones sont des structures complexes constituées de neurones artificiels qui peuvent accepter plusieurs entrées pour produire une seule sortie. C'est le travail principal d'un réseau de neurones - transformer l'entrée en une sortie significative. Habituellement, un réseau de neurones se compose d'une couche d'entrée et de sortie avec une ou plusieurs couches cachées à l'intérieur.

Dans un réseau de neurones, tous les neurones s'influencent mutuellement et sont donc tous connectés. Le réseau peut reconnaître et observer chaque aspect de l'ensemble de données à portée de main et comment les différentes parties de données peuvent ou non être liées les unes aux autres. C'est ainsi que les réseaux de neurones sont capables de trouver des modèles extrêmement complexes dans de vastes volumes de données.

Lire : Apprentissage automatique vs réseaux de neurones

Dans un réseau de neurones, le flux d'informations se produit de deux manières -

• Réseaux Feedforward : dans ce modèle, les signaux ne voyagent que dans une seule direction, vers la couche de sortie. Les réseaux Feedforward ont une couche d'entrée et une seule couche de sortie avec zéro ou plusieurs couches cachées. Ils sont largement utilisés dans la reconnaissance de formes.
• Réseaux de rétroaction : dans ce modèle, les réseaux récurrents ou interactifs utilisent leur état interne (mémoire) pour traiter la séquence d'entrées. Dans ceux-ci, les signaux peuvent voyager dans les deux sens à travers les boucles (couche(s) cachée(s)) du réseau. Ils sont généralement utilisés dans les séries chronologiques et les tâches séquentielles.

Réseau de neurones : composants

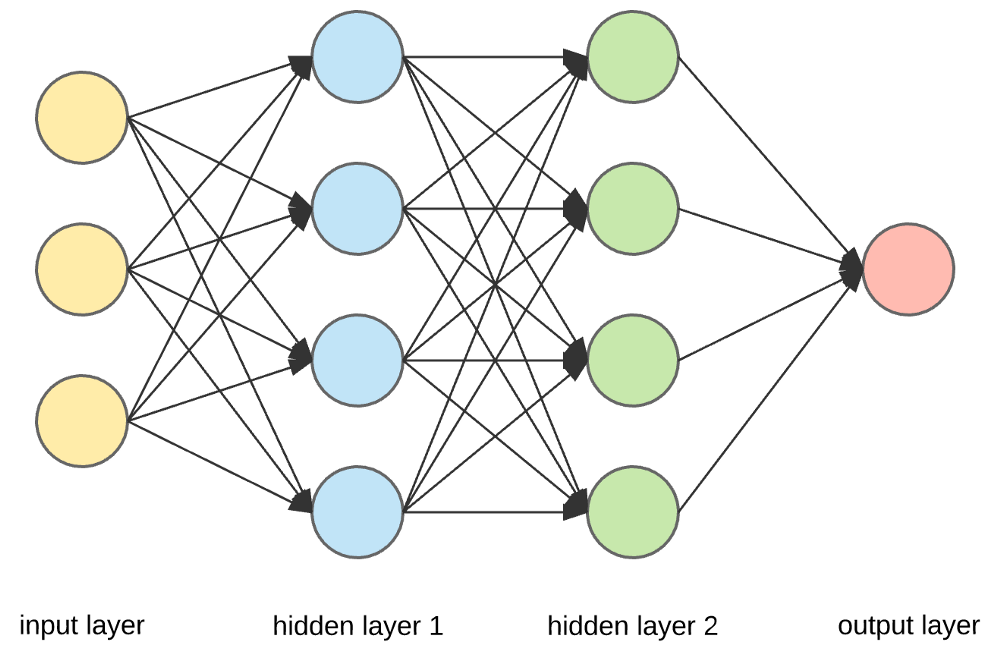
La source

Couches d'entrée, neurones et poids -

Dans l'image ci-dessus, la couche jaune la plus externe est la couche d'entrée. Un neurone est l'unité de base d'un réseau de neurones. Ils reçoivent une entrée d'une source externe ou d'autres nœuds. Chaque nœud est connecté à un autre nœud de la couche suivante, et chacune de ces connexions a un poids particulier. Des poids sont attribués à un neurone en fonction de son importance relative par rapport aux autres entrées.

Lorsque toutes les valeurs de nœud de la couche jaune sont multipliées (avec leur poids) et résumées, cela génère une valeur pour la première couche masquée. Sur la base de la valeur résumée, la couche bleue a une fonction "d'activation" prédéfinie qui détermine si oui ou non ce nœud sera "activé" et à quel point il sera "actif".

Comprenons cela en utilisant une tâche quotidienne simple - faire du thé. Dans le processus de fabrication du thé, les ingrédients utilisés pour fabriquer le thé (eau, feuilles de thé, lait, sucre et épices) sont les «neurones» car ils constituent les points de départ du processus. La quantité de chaque ingrédient représente le « poids ». Une fois que vous avez mis les feuilles de thé dans l'eau et ajouté le sucre, les épices et le lait dans la casserole, tous les ingrédients se mélangent et se transforment en un autre état. Ce processus de transformation représente la "fonction d'activation".

Apprenez-en plus à propos de : Apprentissage en profondeur vs réseaux de neurones

Calques cachés et calque de sortie –

La ou les couches masquées entre la couche d'entrée et la couche de sortie sont appelées couches masquées. On l'appelle la couche cachée car elle est toujours cachée du monde extérieur. Le calcul principal d'un réseau de neurones a lieu dans les couches cachées. Ainsi, la couche cachée prend toutes les entrées de la couche d'entrée et effectue le calcul nécessaire pour générer un résultat. Ce résultat est ensuite transmis à la couche de sortie afin que l'utilisateur puisse visualiser le résultat du calcul.

Dans notre exemple de fabrication de thé, lorsque nous mélangeons tous les ingrédients, la formulation change d'état et de couleur en chauffant. Les ingrédients représentent les couches cachées. Ici, le chauffage représente le processus d'activation qui donne finalement le résultat - le thé.

Réseau de neurones : algorithmes

Dans un réseau de neurones, le processus d'apprentissage (ou de formation) est initié en divisant les données en trois ensembles différents :

• Ensemble de données d'entraînement - Cet ensemble de données permet au réseau de neurones de comprendre les poids entre les nœuds.
• Ensemble de données de validation – Cet ensemble de données est utilisé pour affiner les performances du réseau de neurones.
• Ensemble de données de test - Cet ensemble de données est utilisé pour déterminer la précision et la marge d'erreur du réseau neuronal.

Une fois les données segmentées en ces trois parties, des algorithmes de réseau de neurones leur sont appliqués pour former le réseau de neurones. La procédure utilisée pour faciliter le processus de formation dans un réseau de neurones est connue sous le nom d'optimisation, et l'algorithme utilisé est appelé l'optimiseur. Il existe différents types d'algorithmes d'optimisation, chacun avec ses caractéristiques et aspects uniques tels que les besoins en mémoire, la précision numérique et la vitesse de traitement.

Avant de nous plonger dans la discussion sur les différents algorithmes de réseau de neurones , comprenons d'abord le problème d'apprentissage.

A lire aussi : Applications de réseaux de neurones dans le monde réel

Qu'est-ce que le problème d'apprentissage ?

Nous représentons le problème d'apprentissage en termes de minimisation d'un indice de perte ( f ). Ici, « f » est la fonction qui mesure les performances d'un réseau de neurones sur un ensemble de données donné. Généralement, l'indice de perte se compose d'un terme d'erreur et d'un terme de régularisation. Alors que le terme d'erreur évalue la façon dont un réseau de neurones s'adapte à un ensemble de données, le terme de régularisation aide à prévenir le problème de surajustement en contrôlant la complexité effective du réseau de neurones.

La fonction de perte [ f(w ] dépend des paramètres adaptatifs – poids et biais – du réseau de neurones. Ces paramètres peuvent être regroupés en un seul vecteur de poids à n dimensions ( w ).

Voici une représentation graphique de la fonction de perte :

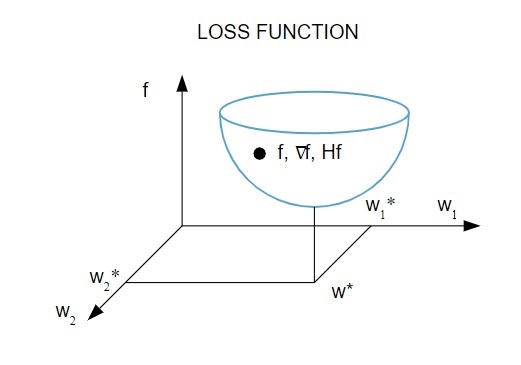
La source

Selon ce diagramme, le minimum de la fonction de perte se produit au point ( w* ). À tout moment, vous pouvez calculer les dérivées premières et secondes de la fonction de perte. Les premières dérivées sont regroupées dans le vecteur gradient et ses composants sont représentés comme suit :

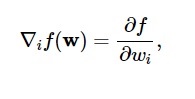
La source

Ici, i = 1,…..,n .

Les dérivées secondes de la fonction de perte sont regroupées dans la matrice hessienne , comme suit :

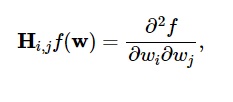
La source

Ici, i,j = 0,1,…

Maintenant que nous savons quel est le problème d'apprentissage, nous pouvons discuter des cinq principales

Algorithmes de réseau de neurones .

1. Optimisation unidimensionnelle

Étant donné que la fonction de perte dépend de plusieurs paramètres, les méthodes d'optimisation unidimensionnelles jouent un rôle déterminant dans la formation du réseau de neurones. Les algorithmes d'entraînement calculent d'abord une direction d'entraînement ( d ), puis calculent le taux d'entraînement ( η ) qui aide à minimiser la perte dans la direction d'entraînement [ f(η) ].

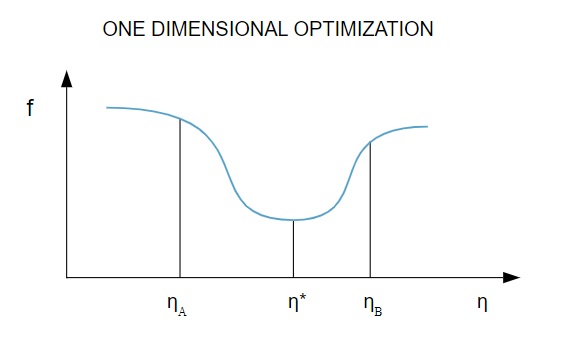
La source

Dans le diagramme, les points η1 et η2 définissent l'intervalle contenant le minimum de f, η* .

Ainsi, les méthodes d'optimisation unidimensionnelle visent à trouver le minimum d'une fonction unidimensionnelle donnée. Deux des algorithmes unidimensionnels les plus couramment utilisés sont la méthode de la section d'or et la méthode de Brent.

Méthode de la section d'or

L'algorithme de recherche du nombre d'or est utilisé pour trouver le minimum ou le maximum d'une fonction à une seule variable [ f(x) ]. Si nous savons déjà qu'une fonction a un minimum entre deux points, alors nous pouvons effectuer une recherche itérative comme nous le ferions dans la recherche de bissection de la racine d'une équation f(x) = 0 . De plus, si nous pouvons trouver trois points ( x0 < x1 < x2 ) correspondant à f(x0) > f(x1) > f(X2) au voisinage du minimum, alors nous pouvons en déduire qu'un minimum existe entre x0 et x2 . Pour connaître ce minimum, on peut considérer un autre point x3 entre x1 et x2 , ce qui nous donnera les résultats suivants :

• Si f(x3) = f3a > f(x1), le minimum est à l'intérieur de l'intervalle x3 – x0 = a + c qui est lié à trois nouveaux points x0 < x1 < x3 (ici x2 est remplacé par x3 ).
• Si f(x3) = f3b > f(x1 ), le minimum est à l'intérieur de l'intervalle x2 – x1 = b lié à trois nouveaux points x1 < x3 < x2 (ici x0 est remplacé par x1 ).

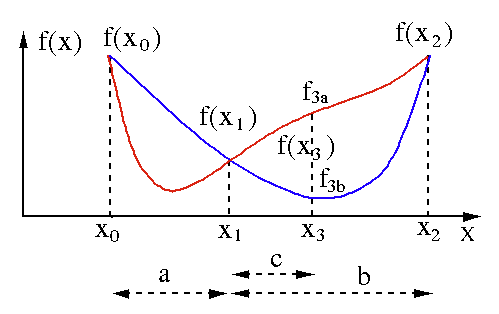
La source

Méthode de Brent

La méthode de Brent est un algorithme de recherche de racine qui combine le bracketing racine , la bissection , la sécante et l' interpolation quadratique inverse . Bien que cet algorithme essaie d'utiliser la méthode sécante à convergence rapide ou l'interpolation quadratique inverse chaque fois que possible, il revient généralement à la méthode de la bissection. Implémentée en Wolfram Language , la méthode de Brent s'exprime comme suit :

Méthode -> Brent dans FindRoot [eqn, x, x0, x1].

Dans la méthode de Brent, nous utilisons un polynôme d'interpolation de Lagrange de degré 2. En 1973, Brent affirmait que cette méthode convergerait toujours, à condition que les valeurs de la fonction soient calculables dans une région spécifique, y compris une racine. S'il y a trois points x1, x2 et x3 , la méthode de Brent ajuste x comme une fonction quadratique de y , en utilisant la formule d'interpolation :

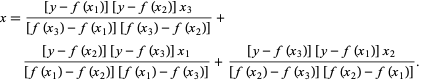
La source

Les estimations de racine suivantes sont obtenues en considérant, produisant ainsi l'équation suivante :

La source

Ici, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] et Q = (T – 1) (R – 1) (S – 1) et,

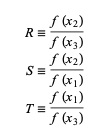
La source

2. Optimisation multidimensionnelle

A présent, nous savons déjà que le problème d'apprentissage pour les réseaux de neurones vise à trouver le vecteur de paramètres ( w* ) pour lequel la fonction de perte ( f ) prend une valeur minimale. Selon les mandats de la condition standard, si le réseau de neurones est au minimum de la fonction de perte, le gradient est le vecteur zéro.

Puisque la fonction de perte est une fonction non linéaire des paramètres, il est impossible de trouver les algorithmes d'apprentissage fermés pour le minimum. Cependant, si nous envisageons de parcourir l'espace des paramètres qui comprend une série d'étapes, à chaque étape, la perte sera réduite en ajustant les paramètres du réseau de neurones.

Dans l'optimisation multidimensionnelle, un réseau de neurones est formé en choisissant un vecteur de paramètre we aléatoire, puis en générant une séquence de paramètres pour garantir que la fonction de perte diminue à chaque itération de l'algorithme. Cette variation de perte entre deux étapes successives est connue sous le nom de « décrément de perte ». Le processus de décrémentation de la perte se poursuit jusqu'à ce que l'algorithme d'apprentissage atteigne ou satisfasse la condition spécifiée.

Voici trois exemples d'algorithmes d'optimisation multidimensionnelle :

Descente graduelle

L'algorithme de descente de gradient est probablement le plus simple de tous les algorithmes d'entraînement. Comme elle s'appuie sur les informations fournies par le vecteur gradient, il s'agit d'une méthode du premier ordre. Dans cette méthode, nous prendrons f[w(i)] = f(i) et ∇f[w(i)] = g(i) . Le point de départ de cet algorithme d'apprentissage est w(0) qui continue de progresser jusqu'à ce que le critère spécifié soit satisfait - il se déplace de w(i) à w(i+1) dans la direction d'apprentissage d(i) = −g(i) . Par conséquent, la descente de gradient itère comme suit :

w(i+1) = w(i)−g(i)η(i),

Ici, je = 0,1,…

Le paramètre η représente le taux d'entraînement. Vous pouvez définir une valeur fixe pour η ou la définir sur la valeur trouvée par l'optimisation unidimensionnelle le long de la direction d'entraînement à chaque étape. Cependant, il est préférable de définir la valeur optimale pour le taux d'apprentissage obtenu par minimisation de ligne à chaque étape.

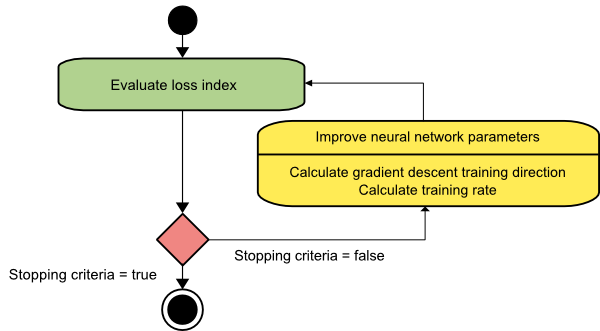
La source

Cet algorithme a de nombreuses limitations car il nécessite de nombreuses itérations pour les fonctions qui ont des structures de vallée longues et étroites. Alors que la fonction de perte décroît le plus rapidement dans la direction du gradient descendant, elle n'assure pas toujours la convergence la plus rapide.

La méthode de Newton

Il s'agit d'un algorithme de second ordre car il exploite la matrice hessienne. La méthode de Newton vise à trouver de meilleures directions d'entraînement en utilisant les dérivées secondes de la fonction de perte. Ici, nous noterons f[w(i)] = f(i), ∇f[w(i)]=g(i) , et Hf[w(i)] = H(i) . Considérons maintenant l'approximation quadratique de f en w(0) en utilisant le développement en série de Taylor, comme ceci :

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

Ici, H(0) est la matrice Hessienne de f calculée au point w(0) . En considérant g = 0 pour le minimum de f(w) , on obtient l'équation suivante :

g = g(0)+H(0)⋅(w−w(0))=0

Par conséquent, nous pouvons voir qu'à partir du vecteur de paramètres w(0), la méthode de Newton itère comme suit :

w(i+1) = w(i)−H(i)−1⋅g(i)

Ici, i = 0,1 ,… et le vecteur H(i)−1⋅g(i) est appelé « pas de Newton ». Vous devez vous rappeler que le changement de paramètre peut aller vers un maximum au lieu d'aller dans le sens d'un minimum. Habituellement, cela se produit si la matrice hessienne n'est pas définie positive, ce qui entraîne une réduction de l'évaluation de la fonction à chaque itération. Cependant, pour éviter ce problème, nous modifions généralement l'équation de la méthode comme suit :

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Ici, je = 0,1 ,….

Vous pouvez soit définir le taux d'entraînement η sur une valeur fixe, soit sur la valeur obtenue via la minimisation de ligne. Ainsi, le vecteur d(i)=H(i)−1⋅g(i) devient la direction d'apprentissage pour la méthode de Newton.

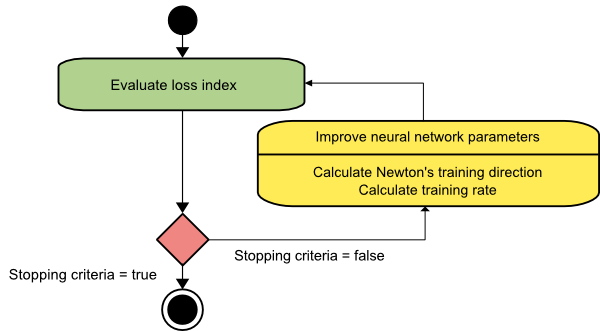
La source

L'inconvénient majeur de la méthode de Newton est que l'évaluation exacte de la Hessienne et de son inverse sont des calculs assez coûteux.

Dégradé conjugué

La méthode du gradient conjugué se situe entre la descente du gradient et la méthode de Newton. Il s'agit d'un algorithme intermédiaire - s'il vise à accélérer le facteur de convergence lente de la méthode de descente de gradient, il élimine également le besoin d'informations concernant l'évaluation, le stockage et l'inversion de la matrice hessienne habituellement requises dans la méthode de Newton.

L'algorithme d'apprentissage du gradient conjugué effectue la recherche dans les directions conjuguées qui offrent une convergence plus rapide que les directions de descente de gradient. Ces directions d'entraînement sont conjuguées conformément à la matrice hessienne. Ici, d désigne le vecteur de direction d'entraînement. Si nous partons d'un vecteur de paramètres initial [w(0)] et d'un vecteur de direction d'entraînement initial [d(0)=−g(0)] , la méthode du gradient conjugué génère une séquence de directions d'entraînement représentées par :

d(i+1) = g(i+1)+d(i)⋅γ(i),

Ici, i = 0,1 ,… et γ est le paramètre conjugué. La direction d'apprentissage pour tous les algorithmes de gradient conjugué est périodiquement réinitialisée au négatif du gradient. Les paramètres sont améliorés et le taux d'entraînement ( η ) est obtenu via la minimisation de la ligne, selon l'expression ci-dessous :

w(i+1) = w(i)+d(i)⋅η(i)

Ici, je = 0,1 ,…

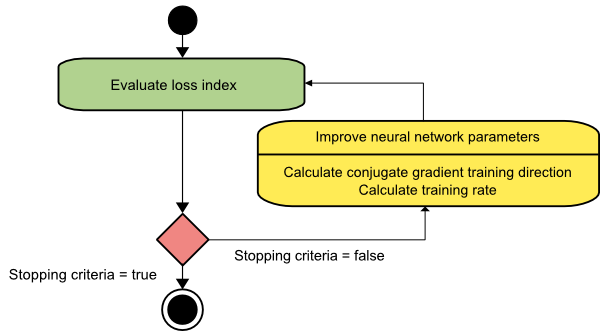
La source

Conclusion

Chaque algorithme présente des avantages et des inconvénients uniques. Ce ne sont que quelques algorithmes utilisés pour former les réseaux de neurones, et leurs fonctions ne démontrent que la pointe de l'iceberg - à mesure que les cadres d'apprentissage en profondeur progressent, les fonctionnalités de ces algorithmes évoluent également.

Si vous souhaitez en savoir plus sur les réseaux de neurones, les programmes d'apprentissage automatique et l'IA , consultez le programme Executive PG d'IIIT-B & upGrad en apprentissage automatique et en IA , conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, statut d'ancien IIIT-B, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.