Red neuronal: arquitectura, componentes y algoritmos principales

Las redes neuronales artificiales (ANN) constituyen una parte integral del proceso de aprendizaje profundo. Están inspirados en la estructura neurológica del cerebro humano. Según AILabPage , las ANN son "códigos informáticos complejos escritos con una cantidad de elementos de procesamiento simples y altamente interconectados que se inspiran en la estructura biológica del cerebro humano para simular modelos de datos (información) de trabajo y procesamiento del cerebro humano".

Únase a las mejores certificaciones de aprendizaje automático en línea de las principales universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.

El aprendizaje profundo se centra en cinco redes neuronales principales, que incluyen:

• Perceptrón multicapa
• Red de base radial
• Redes neuronales recurrentes
• Redes adversarias generativas
• Redes Neuronales Convolucionales.

Red neuronal: arquitectura

Las redes neuronales son estructuras complejas hechas de neuronas artificiales que pueden recibir múltiples entradas para producir una única salida. Este es el trabajo principal de una red neuronal: transformar la entrada en una salida significativa. Por lo general, una red neuronal consta de una capa de entrada y salida con una o varias capas ocultas en su interior.

En una Red Neuronal, todas las neuronas se influyen entre sí y, por lo tanto, están todas conectadas. La red puede reconocer y observar cada aspecto del conjunto de datos disponible y cómo las diferentes partes de los datos pueden o no relacionarse entre sí. Así es como las Redes Neuronales son capaces de encontrar patrones extremadamente complejos en grandes volúmenes de datos.

Leer: Aprendizaje automático frente a redes neuronales

En una red neuronal, el flujo de información se produce de dos maneras:

• Feedforward Networks: En este modelo, las señales solo viajan en una dirección, hacia la capa de salida. Feedforward Networks tiene una capa de entrada y una única capa de salida con cero o varias capas ocultas. Son ampliamente utilizados en el reconocimiento de patrones.
• Redes de retroalimentación: en este modelo, las redes recurrentes o interactivas usan su estado interno (memoria) para procesar la secuencia de entradas. En ellos, las señales pueden viajar en ambas direcciones a través de los bucles (capa/s oculta/s) de la red. Por lo general, se utilizan en series de tiempo y tareas secuenciales.

Red neuronal: componentes

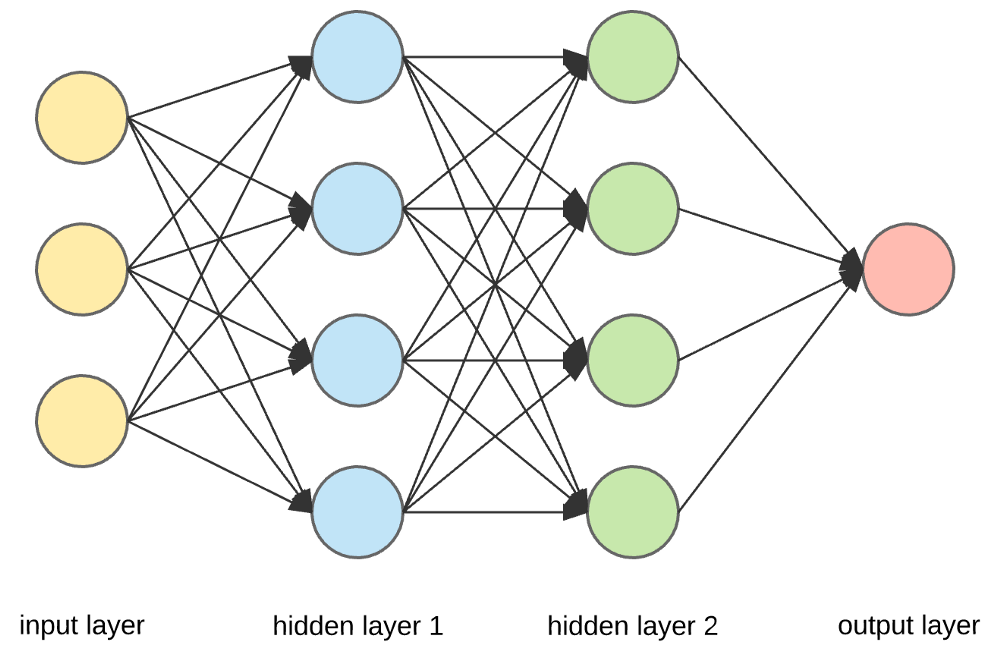
Fuente

Capas de entrada, neuronas y pesos :

En la imagen anterior, la capa amarilla más externa es la capa de entrada. Una neurona es la unidad básica de una red neuronal. Reciben información de una fuente externa u otros nodos. Cada nodo está conectado con otro nodo de la siguiente capa, y cada conexión tiene un peso particular. Los pesos se asignan a una neurona en función de su importancia relativa frente a otras entradas.

Cuando todos los valores de nodo de la capa amarilla se multiplican (junto con su peso) y se resumen, genera un valor para la primera capa oculta. Según el valor resumido, la capa azul tiene una función de "activación" predefinida que determina si este nodo se "activará" o no y qué tan "activo" estará.

Entendamos esto usando una simple tarea cotidiana: preparar té. En el proceso de elaboración del té, los ingredientes que se utilizan para preparar el té (agua, hojas de té, leche, azúcar y especias) son las “neuronas”, ya que constituyen los puntos de partida del proceso. La cantidad de cada ingrediente representa el "peso". Una vez que pongas las hojas de té en el agua y agregues el azúcar, las especias y la leche en la sartén, todos los ingredientes se mezclarán y se transformarán en otro estado. Este proceso de transformación representa la “función de activación”.

Más información sobre: ​​aprendizaje profundo frente a redes neuronales

Capas ocultas y capa de salida :

La capa o capas ocultas entre la capa de entrada y la capa de salida se conoce como capa oculta. Se llama la capa oculta ya que siempre está oculta del mundo exterior. El cómputo principal de una Red Neuronal tiene lugar en las capas ocultas. Entonces, la capa oculta toma todas las entradas de la capa de entrada y realiza el cálculo necesario para generar un resultado. Luego, este resultado se envía a la capa de salida para que el usuario pueda ver el resultado del cálculo.

En nuestro ejemplo de preparación de té, cuando mezclamos todos los ingredientes, la formulación cambia de estado y color al calentarla. Los ingredientes representan las capas ocultas. Aquí el calentamiento representa el proceso de activación que finalmente entrega el resultado: el té.

Red Neuronal: Algoritmos

En una Red Neuronal, el proceso de aprendizaje (o entrenamiento) se inicia dividiendo los datos en tres conjuntos diferentes:

• Conjunto de datos de entrenamiento: este conjunto de datos permite que la red neuronal comprenda los pesos entre los nodos.
• Conjunto de datos de validación: este conjunto de datos se utiliza para ajustar el rendimiento de la red neuronal.
• Conjunto de datos de prueba: este conjunto de datos se utiliza para determinar la precisión y el margen de error de la red neuronal.

Una vez que los datos se segmentan en estas tres partes, se les aplican algoritmos de red neuronal para entrenar la red neuronal. El procedimiento utilizado para facilitar el proceso de entrenamiento en una Red Neuronal se conoce como optimización, y el algoritmo utilizado se denomina optimizador. Existen diferentes tipos de algoritmos de optimización, cada uno con sus características y aspectos únicos, como los requisitos de memoria, la precisión numérica y la velocidad de procesamiento.

Antes de sumergirnos en la discusión de los diferentes algoritmos de redes neuronales , comprendamos primero el problema de aprendizaje.

Lea también : Aplicaciones de redes neuronales en el mundo real

¿Qué es el problema de aprendizaje?

Representamos el problema de aprendizaje en términos de la minimización de un índice de pérdida ( f ). Aquí, " f " es la función que mide el rendimiento de una red neuronal en un conjunto de datos determinado. Generalmente, el índice de pérdida consta de un término de error y un término de regularización. Mientras que el término de error evalúa cómo una red neuronal se ajusta a un conjunto de datos, el término de regularización ayuda a prevenir el problema de sobreajuste al controlar la complejidad efectiva de la red neuronal.

La función de pérdida [ f(w ] depende de los parámetros adaptativos (pesos y sesgos) de la Red neuronal Estos parámetros se pueden agrupar en un solo vector de peso n-dimensional ( w ).

Aquí hay una representación pictórica de la función de pérdida:

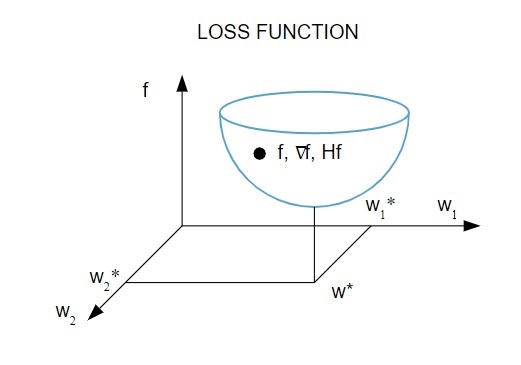
Fuente

De acuerdo con este diagrama, el mínimo de la función de pérdida ocurre en el punto ( w* ). En cualquier punto, puede calcular las derivadas primera y segunda de la función de pérdida. Las primeras derivadas se agrupan en el vector gradiente y sus componentes se representan como:

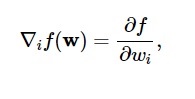
Fuente

Aquí, i = 1,…..,n .

Las segundas derivadas de la función de pérdida se agrupan en la matriz Hessiana , así:

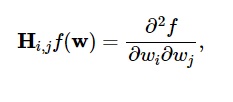
Fuente

Aquí, i,j = 0,1,…

Ahora que sabemos cuál es el problema de aprendizaje, podemos discutir los cinco principales

Algoritmos de redes neuronales .

1. Optimización unidimensional

Dado que la función de pérdida depende de múltiples parámetros, los métodos de optimización unidimensionales son fundamentales para entrenar la red neuronal. Los algoritmos de entrenamiento primero calculan una dirección de entrenamiento ( d ) y luego calculan la tasa de entrenamiento ( η ) que ayuda a minimizar la pérdida en la dirección de entrenamiento [ f(η) ].

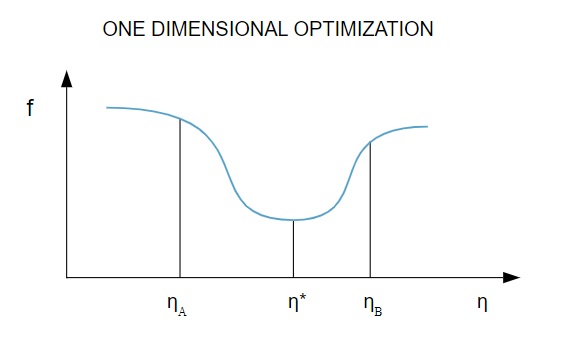
Fuente

En el diagrama, los puntos η1 y η2 definen el intervalo que contiene el mínimo de f, η* .

Por lo tanto, los métodos de optimización unidimensional tienen como objetivo encontrar el mínimo de una función unidimensional dada. Dos de los algoritmos unidimensionales más utilizados son el Método de la Sección Dorada y el Método de Brent.

Método de la sección áurea

El algoritmo de búsqueda de la sección dorada se usa para encontrar el mínimo o el máximo de una función de una sola variable [ f(x) ]. Si ya sabemos que una función tiene un mínimo entre dos puntos, entonces podemos realizar una búsqueda iterativa tal como lo haríamos en la búsqueda de bisección de la raíz de una ecuación f(x) = 0 . Además, si podemos encontrar tres puntos ( x0 < x1 < x2 ) correspondientes a f(x0) > f(x1) > f(X2) en la vecindad del mínimo, entonces podemos deducir que existe un mínimo entre x0 y x2 . Para encontrar este mínimo, podemos considerar otro punto x3 entre x1 y x2 , lo que nos dará los siguientes resultados:

• Si f(x3) = f3a > f(x1), el mínimo está dentro del intervalo x3 – x0 = a + c que se relaciona con tres nuevos puntos x0 < x1 < x3 (aquí se reemplaza x2 por x3 ).
• Si f(x3) = f3b > f(x1 ), el mínimo está dentro del intervalo x2 – x1 = b relacionado con tres nuevos puntos x1 < x3 < x2 (aquí se reemplaza x0 por x1 ).

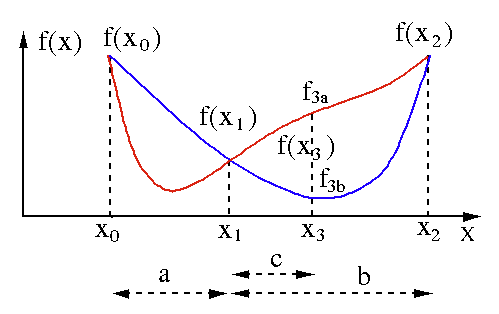
Fuente

Método de Brent

El método de Brent es un algoritmo de búsqueda de raíces que combina paréntesis de raíces , bisección , secante e interpolación cuadrática inversa . Aunque este algoritmo trata de utilizar el método de la secante de convergencia rápida o la interpolación cuadrática inversa siempre que sea posible, por lo general vuelve al método de bisección. Implementado en Wolfram Language , el método de Brent se expresa como:

Método -> Brent en FindRoot [eqn, x, x0, x1].

En el método de Brent, usamos un polinomio de interpolación de Lagrange de grado 2. En 1973, Brent afirmó que este método siempre convergerá, siempre que los valores de la función sean computables dentro de una región específica, incluida una raíz. Si hay tres puntos x1, x2 y x3 , el método de Brent ajusta x como una función cuadrática de y , usando la fórmula de interpolación:

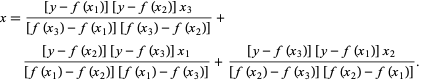
Fuente

Las estimaciones posteriores de la raíz se logran considerando, produciendo así la siguiente ecuación:

Fuente

Aquí, P = S [ T(R – T) (x3 – x2) – (1 – R) (x2 -x1) ] y Q = (T – 1) (R – 1) (S – 1) y,

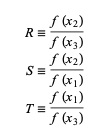
Fuente

2. Optimización multidimensional

A estas alturas, ya sabemos que el problema de aprendizaje de Redes Neuronales tiene como objetivo encontrar el vector de parámetros ( w* ) para el cual la función de pérdida ( f ) toma un valor mínimo. De acuerdo con los mandatos de la condición estándar, si la red neuronal está en un mínimo de la función de pérdida, el gradiente es el vector cero.

Dado que la función de pérdida es una función no lineal de los parámetros, es imposible encontrar algoritmos de entrenamiento cerrados para el mínimo. Sin embargo, si consideramos buscar a través del espacio de parámetros que incluye una serie de pasos, en cada paso, la pérdida se reducirá ajustando los parámetros de la Red Neuronal.

En la optimización multidimensional, una red neuronal se entrena eligiendo un vector de parámetros aleatorio y luego generando una secuencia de parámetros para garantizar que la función de pérdida disminuya con cada iteración del algoritmo. Esta variación de pérdida entre dos pasos posteriores se conoce como “decremento de pérdida”. El proceso de disminución de pérdidas continúa hasta que el algoritmo de entrenamiento alcanza o satisface la condición especificada.

Aquí hay tres ejemplos de algoritmos de optimización multidimensional:

Descenso de gradiente

El algoritmo de descenso de gradiente es probablemente el más simple de todos los algoritmos de entrenamiento. Como se basa en la información proporcionada por el vector de gradiente, es un método de primer orden. En este método, tomaremos f[w(i)] = f(i) y ∇f[w(i)] = g(i) . El punto de partida de este algoritmo de entrenamiento es w(0) que continúa progresando hasta que se satisface el criterio especificado: se mueve de w(i) a w(i+1) en la dirección de entrenamiento d(i) = −g(i) . Por lo tanto, el descenso del gradiente itera de la siguiente manera:

w(i+1) = w(i)−g(i)η(i),

Aquí, i = 0,1,…

El parámetro η representa la tasa de entrenamiento. Puede establecer un valor fijo para η o establecerlo en el valor encontrado por la optimización unidimensional a lo largo de la dirección de entrenamiento en cada paso. Sin embargo, se prefiere establecer el valor óptimo para la tasa de entrenamiento lograda por la minimización de líneas en cada paso.

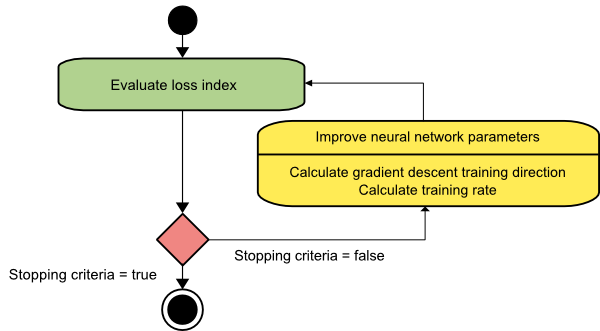
Fuente

Este algoritmo tiene muchas limitaciones ya que requiere numerosas iteraciones para funciones que tienen estructuras de valle largas y estrechas. Si bien la función de pérdida disminuye más rápidamente en la dirección del gradiente cuesta abajo, no siempre asegura la convergencia más rápida.

método de newton

Este es un algoritmo de segundo orden ya que aprovecha la matriz hessiana. El método de Newton tiene como objetivo encontrar mejores direcciones de entrenamiento haciendo uso de las segundas derivadas de la función de pérdida. Aquí, denotaremos f[w(i)] = f(i), ∇f[w(i)]=g(i) y Hf[w(i)] = H(i) . Ahora, consideraremos la aproximación cuadrática de f en w(0) usando la expansión de la serie de Taylor, así:

f = f(0)+g(0)⋅[w−w(0)] + 0.5⋅[w−w(0)]2⋅H(0)

Aquí, H(0) es la matriz hessiana de f calculada en el punto w(0) . Al considerar g = 0 para el mínimo de f(w) , obtenemos la siguiente ecuación:

g = g(0)+H(0)⋅(w−w(0))=0

Como resultado, podemos ver que a partir del vector de parámetros w(0), el método de Newton itera de la siguiente manera:

w(i+1) = w(i)−H(i)−1⋅g(i)

Aquí, i = 0,1 ,… y el vector H(i)−1⋅g(i) se denomina “Paso de Newton”. Debe recordar que el cambio de parámetro puede moverse hacia un máximo en lugar de ir en la dirección de un mínimo. Por lo general, esto sucede si la matriz hessiana no es definida positiva, lo que hace que la evaluación de la función se reduzca en cada iteración. Sin embargo, para evitar este problema, generalmente modificamos la ecuación del método de la siguiente manera:

w(i+1) = w(i)−(H(i)−1⋅g(i))η

Aquí, i = 0,1 ,….

Puede establecer la tasa de entrenamiento η en un valor fijo o el valor obtenido a través de la minimización de líneas. Entonces, el vector d(i)=H(i)−1⋅g(i) se convierte en la dirección de entrenamiento para el método de Newton.

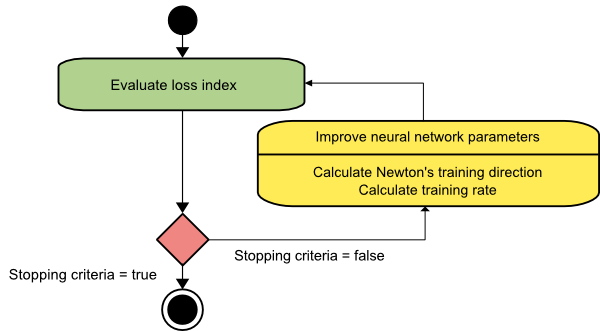
Fuente

El principal inconveniente del método de Newton es que la evaluación exacta de la arpillera y su inversa son cálculos bastante costosos.

Gradiente conjugado

El método del gradiente conjugado se encuentra entre el descenso del gradiente y el método de Newton. Es un algoritmo intermedio: si bien tiene como objetivo acelerar el factor de convergencia lento del método de descenso de gradiente, también elimina la necesidad de los requisitos de información relacionados con la evaluación, el almacenamiento y la inversión de la matriz hessiana que generalmente se requieren en el método de Newton.

El algoritmo de entrenamiento de gradiente conjugado realiza la búsqueda en las direcciones conjugadas que ofrece una convergencia más rápida que las direcciones de descenso de gradiente. Estas direcciones de entrenamiento se conjugan de acuerdo con la matriz de Hesse. Aquí, d denota el vector de dirección de entrenamiento. Si comenzamos con un vector de parámetro inicial [w(0)] y un vector de dirección de entrenamiento inicial [d(0)=−g(0)] , el método de gradiente conjugado genera una secuencia de direcciones de entrenamiento representadas como:

d(i+1) = g(i+1)+d(i)⋅γ(i),

Aquí, i = 0,1 ,… y γ es el parámetro conjugado. La dirección de entrenamiento para todos los algoritmos de gradiente conjugado se restablece periódicamente al negativo del gradiente. Se mejoran los parámetros y se logra la tasa de entrenamiento ( η ) mediante la minimización de líneas, según la expresión que se muestra a continuación:

w(i+1) = w(i)+d(i)⋅η(i)

Aquí, i = 0,1 ,…

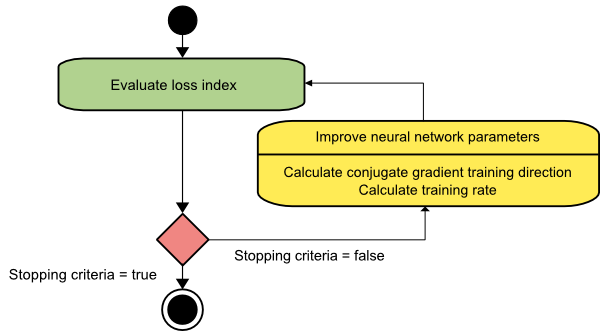
Fuente

Conclusión

Cada algoritmo viene con ventajas y desventajas únicas. Estos son solo algunos algoritmos utilizados para entrenar redes neuronales, y sus funciones solo demuestran la punta del iceberg: a medida que avanzan los marcos de aprendizaje profundo , también lo harán las funcionalidades de estos algoritmos.

Si está interesado en obtener más información sobre redes neuronales, programas de aprendizaje automático e IA , consulte el Programa Executive PG de IIIT-B y upGrad en Aprendizaje automático e IA, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, estado de ex alumnos de IIIT-B, más de 5 proyectos prácticos finales y asistencia laboral con las mejores empresas.