Un tuffo nell'apprendimento per rinforzo

Diamo un'occhiata approfondita all'apprendimento per rinforzo. In questo articolo affronteremo un problema concreto con le librerie moderne come TensorFlow, TensorBoard, Keras e OpenAI gym. Vedrai come implementare uno degli algoritmi fondamentali chiamati deep $Q$-learning per apprenderne il funzionamento interno. Per quanto riguarda l'hardware, l'intero codice funzionerà su un tipico PC e utilizzerà tutti i core della CPU trovati (questo è gestito immediatamente da TensorFlow).

Il problema si chiama Mountain Car: un'auto si trova su una pista unidimensionale, posizionata tra due montagne. L'obiettivo è salire sulla montagna a destra (raggiungendo la bandiera). Tuttavia, il motore dell'auto non è abbastanza potente per scalare la montagna in un unico passaggio. Pertanto, l'unico modo per avere successo è guidare avanti e indietro per aumentare lo slancio.

Questo problema è stato scelto perché è abbastanza semplice trovare una soluzione con l'apprendimento per rinforzo in pochi minuti su un singolo core della CPU. Tuttavia, è abbastanza complesso per essere un buon rappresentante.

In primo luogo, fornirò un breve riassunto di ciò che fa l'apprendimento per rinforzo in generale. Quindi, tratteremo i termini di base ed esprimeremo il nostro problema con essi. Successivamente, descriverò l'algoritmo di apprendimento profondo $Q$ e lo implementeremo per risolvere il problema.

Nozioni di base sull'apprendimento per rinforzo

L'apprendimento per rinforzo nelle parole più semplici è l'apprendimento per tentativi ed errori. Il personaggio principale è chiamato "agente", che sarebbe un'auto nel nostro problema. L'agente compie un'azione in un ambiente e riceve una nuova osservazione e una ricompensa per quell'azione. Le azioni che portano a ricompense maggiori sono rafforzate, da cui il nome. Come per molte altre cose nell'informatica, anche questa è stata ispirata dall'osservazione di creature viventi.

Le interazioni dell'agente con un ambiente sono riassunte nel grafico seguente:

L'agente riceve un'osservazione e una ricompensa per l'azione eseguita. Quindi esegue un'altra azione e esegue il passaggio due. L'ambiente ora restituisce un'osservazione e una ricompensa (probabilmente) leggermente diverse. Ciò continua fino al raggiungimento dello stato terminale, segnalato dall'invio di "fatto" a un agente. L'intera sequenza di osservazioni > azioni > osservazioni_successive > ricompense è chiamata episodio (o traiettoria).

Tornando alla nostra Mountain Car: la nostra macchina è un agente. L'ambiente è un mondo a scatola nera di montagne unidimensionali. L'azione dell'auto si riduce a un solo numero: se positivo, il motore spinge l'auto a destra. Se negativo, spinge l'auto a sinistra. L'agente percepisce un ambiente attraverso un'osservazione: la posizione X e la velocità dell'auto. Se vogliamo che la nostra auto guidi in cima alla montagna, definiamo la ricompensa in un modo conveniente: l'agente ottiene -1 alla sua ricompensa per ogni passo in cui non ha raggiunto l'obiettivo. Quando raggiunge l'obiettivo, l'episodio finisce. Quindi, in effetti, l'agente viene punito per non essere nella posizione che vorremmo che fosse. Più velocemente lo raggiunge, meglio è per lui. L'obiettivo dell'agente è massimizzare la ricompensa totale, che è la somma delle ricompense di un episodio. Quindi se raggiunge il punto desiderato dopo, ad esempio, 110 passi, riceve un ritorno totale di -110, che sarebbe un ottimo risultato per Mountain Car, perché se non raggiunge l'obiettivo, viene punito per 200 passi (quindi un ritorno di -200).

Questa è l'intera formulazione del problema. Ora possiamo darlo agli algoritmi, che sono già abbastanza potenti da risolvere tali problemi in pochi minuti (se ben sintonizzati). Vale la pena notare che non diciamo all'agente come raggiungere l'obiettivo. Non forniamo nemmeno alcun suggerimento (euristica). L'agente troverà un modo (una politica) per vincere da solo.

Impostare l'ambiente

Innanzitutto, copia l'intero codice del tutorial sul tuo disco:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Ora, dobbiamo installare i pacchetti Python che useremo. Per non installarli nel tuo spazio utente (e rischiare collisioni), lo renderemo pulito e li installeremo nell'ambiente conda. Se non hai installato conda, segui https://conda.io/docs/user-guide/install/index.html.

Per creare il nostro ambiente conda:

 conda create -n tutorial python=3.6.5 -y

Per attivarlo:

 source activate tutorial

Dovresti vedere (tutorial) vicino al tuo prompt nella shell. Significa che è attivo un ambiente conda con il nome “tutorial”. D'ora in poi, tutti i comandi dovrebbero essere eseguiti all'interno di quell'ambiente conda.

Ora possiamo installare tutte le dipendenze nel nostro ambiente conda ermetico:

 pip install -r requirements.txt

Abbiamo finito con l'installazione, quindi eseguiamo del codice. Non abbiamo bisogno di implementare noi stessi l'ambiente Mountain Car; la libreria OpenAI Gym fornisce tale implementazione. Vediamo un agente casuale (un agente che esegue azioni casuali) nel nostro ambiente:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Questo è il file see.py ; per eseguirlo, eseguire:

 python see.py

Dovresti vedere un'auto che va avanti e indietro a caso. Ogni episodio sarà composto da 200 passaggi; il rendimento totale sarà -200.

Ora dobbiamo sostituire le azioni casuali con qualcosa di meglio. Ci sono molti algoritmi che si potrebbero usare. Per un tutorial introduttivo, penso che un approccio chiamato deep $Q$-learning sia adatto. Comprendere quel metodo fornisce una solida base per l'apprendimento di altri approcci.

Apprendimento profondo di $Q$

L'algoritmo che useremo è stato descritto per la prima volta nel 2013 da Mnih et al. in Giocare ad Atari con Deep Reinforcement Learning e perfezionato due anni dopo in Controllo a livello umano attraverso Deep Reinforcement Learning. Molti altri lavori si basano su questi risultati, incluso l'attuale algoritmo all'avanguardia Rainbow (2017):

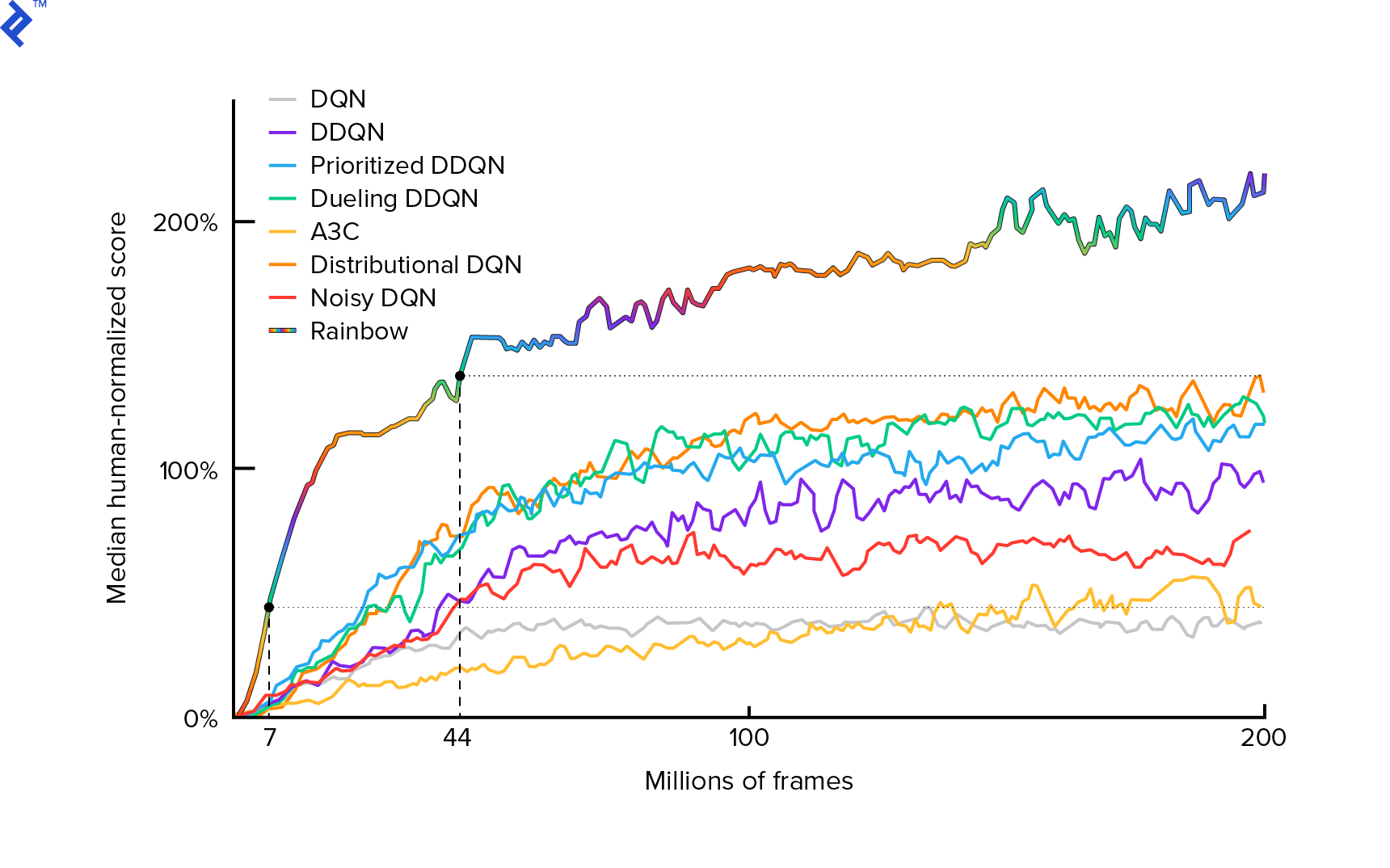
Rainbow ottiene prestazioni sovrumane su molti giochi Atari 2600. Ci concentreremo sulla versione base di DQN, con il minor numero possibile di miglioramenti aggiuntivi, per mantenere questo tutorial di dimensioni ragionevoli.

Una politica, tipicamente indicata con $π(s)$, è una funzione che restituisce le probabilità di intraprendere azioni individuali in un dato stato $s$. Quindi, ad esempio, una polizza Mountain Car casuale restituisce per qualsiasi stato: 50% a sinistra, 50% a destra. Durante il gioco, campioniamo da quella politica (distribuzione) per ottenere azioni reali.

$Q$-learning (Q sta per Quality) si riferisce alla funzione valore-azione denominata $Q_π(s, a)$. Restituisce il rendimento totale di un dato stato $s$, scegliendo l'azione $a$, seguendo una politica concreta $π$. Il rendimento totale è la somma di tutte le ricompense in un episodio (traiettoria).

Se conoscessimo la funzione ottimale $Q$, indicata con $Q^*$, potremmo risolvere il gioco facilmente. Seguiremmo semplicemente le azioni con il valore più alto di $Q^*$, cioè il rendimento atteso più alto. Ciò garantisce che raggiungeremo il massimo rendimento possibile.

Tuttavia, spesso non sappiamo $Q^*$. In questi casi, possiamo approssimarlo - o "apprenderlo" - dalle interazioni con l'ambiente. Questa è la parte "$Q$-learning" nel nome. C'è anche la parola "profondo" in esso perché, per approssimare quella funzione, useremo reti neurali profonde, che sono approssimatori di funzioni universali. Le reti neurali profonde che approssimano i valori $Q$ sono state denominate Deep Q-Networks (DQN). In ambienti semplici (con il numero di stati che si adattano alla memoria), si potrebbe semplicemente usare una tabella invece di una rete neurale per rappresentare la funzione $Q$, nel qual caso sarebbe chiamata "apprendimento tabulare $Q$".

Quindi il nostro obiettivo ora è approssimare la funzione $Q^*$. Useremo l'equazione di Bellman:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ è lo stato dopo $s$. $γ$ (gamma), tipicamente 0,99, è un fattore di sconto (è un iperparametro). Dà un peso minore alle ricompense future (perché sono meno certe delle ricompense immediate con il nostro imperfetto $Q$). L'equazione di Bellman è fondamentale per l'apprendimento profondo di $Q$. Dice che il valore $Q$ per un dato stato e un'azione è una ricompensa $r$ ricevuta dopo aver intrapreso l'azione $a$ più il valore $Q$ più alto per lo stato in cui atterriamo in $s'$. Il massimo è in un certo senso che stiamo scegliendo un'azione $a'$, che porta al rendimento totale più alto da $s'$.

Con l'equazione di Bellman, possiamo usare l'apprendimento supervisionato per approssimare $Q^*$. La funzione $Q$ sarà rappresentata (parametrizzata) da pesi della rete neurale indicati come $θ$ (theta). Un'implementazione semplice richiederebbe uno stato e un'azione come input di rete e output del valore Q. L'inefficienza è che se vogliamo conoscere i valori di $Q$ per tutte le azioni in un dato stato, dobbiamo chiamare $Q$ tante volte quante sono le azioni. C'è un modo molto migliore: prendere solo lo stato come input e restituire i valori $Q$ per tutte le possibili azioni. Grazie a ciò, possiamo ottenere valori $Q$ per tutte le azioni in un solo passaggio in avanti.

Iniziamo ad addestrare la rete $Q$ con pesi casuali. Dall'ambiente si ottengono molte transizioni (o “esperienze”). Queste sono tuple di (stato, azione, stato successivo, ricompensa) o, in breve, ($s$, $a$, $s'$, $r$). Ne archiviamo migliaia in un buffer ad anello chiamato "experience replay". Quindi, campioniamo le esperienze da quel buffer con il desiderio che l'equazione di Bellman conterrà per loro. Avremmo potuto saltare il buffer e applicare le esperienze una per una (questo è chiamato "online" o "on-policy"); il problema è che le esperienze successive sono altamente correlate tra loro e DQN si allena male quando ciò si verifica. Ecco perché è stato introdotto il replay dell'esperienza (un approccio "offline", "off-policy") per rompere questa correlazione di dati. Il codice della nostra più semplice implementazione del buffer ad anello può essere trovato nel file replay_buffer.py , ti incoraggio a leggerlo.

All'inizio, poiché i pesi della nostra rete neurale erano casuali, il valore del lato sinistro dell'equazione di Bellman sarà lontano dal lato destro. La differenza al quadrato sarà la nostra funzione di perdita. Minimizziamo la funzione di perdita modificando i pesi della rete neurale $θ$. Scriviamo la nostra funzione di perdita:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

È un'equazione di Bellman riscritta. Diciamo che abbiamo provato un'esperienza ($s$, sinistra, $s'$, -1) dal replay dell'esperienza Mountain Car. Facciamo un passaggio in avanti attraverso la nostra rete $Q$ con lo stato $s$ e per l'azione a sinistra ci dà -120, per esempio. Quindi, $Q(s, \textrm{sinistra}) = -120$. Quindi inseriamo $s'$ nella rete, che ci dà, ad esempio, -130 per sinistra e -122 per destra. Quindi chiaramente l'azione migliore per $s'$ è giusta, quindi $\textrm{max}_{a'}Q(s', a') = -122$. Sappiamo che $r$, questa è la vera ricompensa, che era -1. Quindi la nostra previsione di rete $Q$ era leggermente sbagliata, perché $L(θ) = [-120 - 1 + 0.99 ⋅ 122]^2 = (-0.22^2) = 0.0484$. Quindi propaghiamo all'indietro l'errore e correggiamo leggermente i pesi $θ$. Se dovessimo calcolare nuovamente la perdita per la stessa esperienza, ora sarebbe inferiore.

Un'osservazione importante prima di passare al codice. Notiamo che, per aggiornare il nostro DQN, faremo due passaggi in avanti sul DQN... stesso. Questo spesso porta a un apprendimento instabile. Per alleviare ciò, per la previsione $Q$ dello stato successivo, non utilizziamo lo stesso DQN. Ne utilizziamo una versione precedente, che nel codice è chiamata target_model (invece di model , essendo il DQN principale). Grazie a ciò, abbiamo un obiettivo stabile. Aggiorniamo target_model impostandolo per model i pesi ogni 1000 passaggi. Ma il model si aggiorna ad ogni passaggio.

Diamo un'occhiata al codice che crea il modello DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Innanzitutto, la funzione prende le dimensioni dell'azione e dello spazio di osservazione dall'ambiente OpenAI Gym dato. È necessario sapere, ad esempio, quante uscite avrà la nostra rete. Deve essere uguale al numero di azioni. Le azioni sono una codificata a caldo:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Quindi (es.) sinistra sarà [1, 0] e destra sarà [0, 1].

Possiamo vedere che le osservazioni vengono passate come input. Passiamo anche action_mask come secondo input. Come mai? Quando si calcola $Q(s,a)$, è necessario conoscere il valore di $Q$ solo per una determinata azione, non per tutte. action_mask contiene 1 per le azioni che vogliamo passare all'output DQN. Se action_mask ha 0 per qualche azione, il valore $Q$ corrispondente verrà azzerato sull'output. Il livello filtered_output lo sta facendo. Se vogliamo tutti i valori $Q$ (per il calcolo massimo), possiamo semplicemente passare tutti quelli.

Il codice usa keras.layers.Dense per definire un livello completamente connesso. Keras è una libreria Python per l'astrazione di livello superiore su TensorFlow. Sotto il cofano, Keras crea un grafico TensorFlow, con bias, corretta inizializzazione del peso e altre cose di basso livello. Avremmo potuto semplicemente usare TensorFlow grezzo per definire il grafico, ma non sarà un one-liner.

Quindi le osservazioni vengono passate al primo livello nascosto, con attivazioni ReLU (unità lineare rettificata). ReLU(x) è solo una funzione $\textrm{max}(0, x)$. Quel livello è completamente connesso con un secondo identico, hidden_2 . Il livello di output riduce il numero di neuroni al numero di azioni. Alla fine, abbiamo filtered_output , che moltiplica semplicemente l'output con action_mask .

Per trovare i pesi $θ$, utilizzeremo un ottimizzatore chiamato "Adam" con una perdita di errore quadratica media.

Avendo un modello, possiamo usarlo per prevedere i valori $Q$ per determinate osservazioni di stato:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Vogliamo $Q$-valori per tutte le azioni, quindi action_mask è un vettore di uno.

Per fare l'allenamento vero e proprio, useremo fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Il batch contiene esperienze BATCH_SIZE . next_q_values ​​è $Q(s, a)$. q_values ​​è $r + γ \space \textrm{max}_{a'}Q(s', a')$ dall'equazione di Bellman. Le azioni che abbiamo intrapreso sono codificate a caldo e passate come action_mask all'input quando si chiama model.fit() . $y$ è una lettera comune per un "bersaglio" nell'apprendimento supervisionato. Qui stiamo passando i q_values ​​. Faccio q_values[:. None] q_values[:. None] per aumentare la dimensione dell'array perché deve corrispondere alla dimensione dell'array one_hot_actions . Questa è chiamata notazione slice se vuoi saperne di più.

Restituiamo la perdita per salvarla nel file di registro di TensorBoard e visualizzarla successivamente. Ci sono molte altre cose che controlleremo: quanti passi al secondo facciamo, utilizzo totale della RAM, qual è il rendimento medio degli episodi, ecc. Vediamo quei grafici.

In esecuzione

Per visualizzare il file di registro di TensorBoard, dobbiamo prima averne uno. Quindi eseguiamo solo l'allenamento:

 python run.py

Questo stamperà prima il riepilogo del nostro modello. Quindi creerà una directory di registro con la data corrente e inizierà la formazione. Ogni 2000 passi, verrà stampata una logline simile a questa:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Ogni 20.000 valuteremo il nostro modello su 10.000 passaggi:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Dopo 677 episodi e 120.000 passaggi, il rendimento medio degli episodi è migliorato da -200 a -136,75! Sta sicuramente imparando. Che cosa avg_max_q_value è lascio come buon esercizio al lettore. Ma è una statistica molto utile da guardare durante l'allenamento.

Dopo 200.000 passi, la nostra formazione è terminata. Sulla mia CPU a quattro core, ci vogliono circa 20 minuti. Possiamo guardare all'interno della directory del registro delle date-log , ad esempio 06-07-18-39-log . Ci saranno quattro file modello con estensione .h5 . Questa è un'istantanea dei pesi dei grafici TensorFlow, li salviamo ogni 50.000 passaggi per dare un'occhiata in seguito alla politica che abbiamo appreso. Per vederlo:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Per vedere gli altri possibili flag: python run.py --help .

Ora, l'auto sta facendo un lavoro molto migliore nel raggiungere l'obiettivo desiderato. Nella directory date-log c'è anche il file events.out.* . Questo è il file in cui TensorBoard memorizza i suoi dati. Gli scriviamo usando il TensorBoardLogger più semplice definito in loggers.py. Per visualizzare il file degli eventi, è necessario eseguire il server TensorBoard locale:

 tensorboard --logdir=.

--logdir punta semplicemente alla directory in cui ci sono le directory del registro delle date, nel nostro caso, questa sarà la directory corrente, quindi . . TensorBoard stampa l'URL a cui è in ascolto. Se apri http://127.0.0.1:6006, dovresti vedere otto grafici simili a questi:

Avvolgendo

train() fa tutto l'addestramento. Per prima cosa creiamo il modello e riproduciamo il buffer. Quindi, in un ciclo molto simile a quello di see.py , interagiamo con l'ambiente e archiviamo le esperienze nel buffer. L'importante è seguire una politica epsilon-greedy. Potremmo sempre scegliere l'azione migliore in base alla funzione $Q$; tuttavia, ciò scoraggia l'esplorazione, che danneggia le prestazioni complessive. Quindi, per imporre l'esplorazione con probabilità epsilon, eseguiamo azioni casuali:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon è stato impostato all'1%. Dopo 2000 esperienze, il replay si riempie abbastanza per iniziare l'allenamento. Lo facciamo chiamando fit_batch() con un batch casuale di esperienze campionate dal buffer di riproduzione:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Ogni 20.000 passi, valutiamo e registriamo i risultati (la valutazione è con epsilon = 0 , politica totalmente avida):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

L'intero codice è di circa 300 righe e run.py contiene circa 250 delle più importanti.

Si può notare che ci sono molti iperparametri:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

E non sono nemmeno tutti. C'è anche un'architettura di rete: abbiamo usato due livelli nascosti con 32 neuroni, attivazioni ReLU e ottimizzatore Adam, ma ci sono molte altre opzioni. Anche piccoli cambiamenti possono avere un enorme impatto sulla formazione. È possibile dedicare molto tempo all'ottimizzazione degli iperparametri. In una recente competizione OpenAI, un concorrente al secondo posto ha scoperto che è possibile quasi raddoppiare il punteggio di Rainbow dopo l'ottimizzazione dell'iperparametro. Naturalmente, bisogna ricordare che è facile overfitting. Attualmente, gli algoritmi di rinforzo stanno lottando con il trasferimento di conoscenze in ambienti simili. La nostra Mountain Car non è generalizzata a tutti i tipi di montagne in questo momento. Puoi effettivamente modificare l'ambiente OpenAI Gym e vedere fino a che punto l'agente può generalizzare.

Un altro esercizio sarà trovare un insieme di iperparametri migliore del mio. È sicuramente possibile. Tuttavia, una sessione di allenamento non sarà sufficiente per giudicare se il tuo cambiamento è un miglioramento. Di solito c'è una grande differenza tra le corse di allenamento; la varianza è grande. Avresti bisogno di molte corse per determinare che qualcosa è meglio. Se desideri saperne di più su un argomento così importante come la riproducibilità, ti incoraggio a leggere Deep Reinforcement Learning that Matters. Invece di ottimizzare manualmente, possiamo automatizzare questo processo in una certa misura, se siamo disposti a spendere più potenza di calcolo per il problema. Un approccio semplice consiste nel preparare un promettente intervallo di valori per alcuni iperparametri e quindi eseguire una ricerca nella griglia (verificando le loro combinazioni), con i corsi di formazione eseguiti in parallelo. La parallelizzazione stessa è un argomento importante di per sé in quanto è fondamentale per prestazioni elevate.

Deep $Q$-learning rappresenta una grande famiglia di algoritmi di apprendimento per rinforzo che utilizzano l'iterazione del valore. Abbiamo cercato di approssimare la funzione $Q$ e l'abbiamo usata in modo avido per la maggior parte del tempo. C'è un'altra famiglia che usa l'iterazione dei criteri. Non si concentrano sull'approssimazione della funzione $Q$, ma sulla ricerca diretta della politica ottimale $π^*$. Per vedere dove si inserisce l'iterazione del valore nel panorama degli algoritmi di apprendimento per rinforzo:

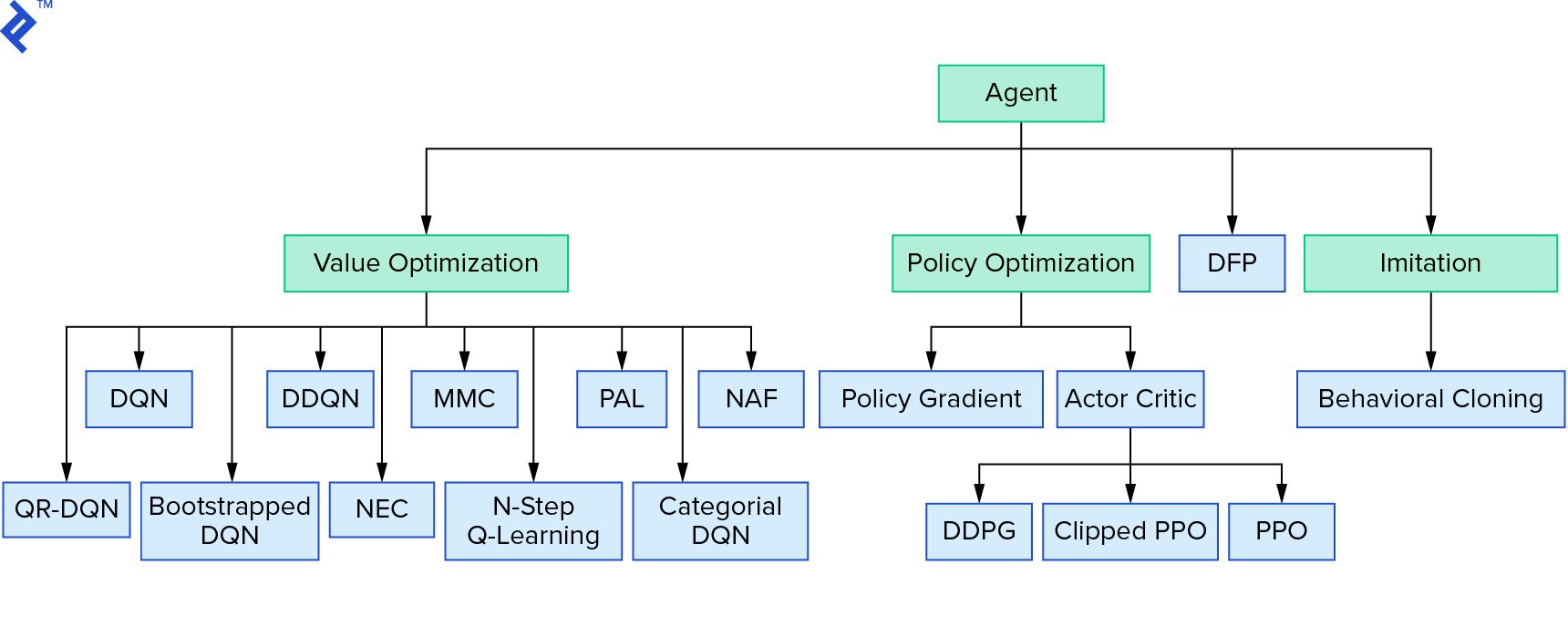
I tuoi pensieri potrebbero essere che l'apprendimento per rinforzo profondo sembra fragile. Avrai ragione; ci sono molti problemi. Puoi fare riferimento a L'apprendimento per rinforzo profondo non funziona ancora e l'apprendimento per rinforzo non ha mai funzionato e "profondo" ha solo aiutato un po '.

Questo conclude il tutorial. Abbiamo implementato il nostro DQN di base per scopi di apprendimento. Un codice molto simile può essere utilizzato per ottenere buone prestazioni in alcuni giochi Atari. Nelle applicazioni pratiche, spesso si prendono implementazioni testate e ad alte prestazioni, ad esempio una dalle linee di base di OpenAI. Se desideri vedere quali sfide si possono affrontare quando si tenta di applicare l'apprendimento per rinforzo profondo in un ambiente più complesso, puoi leggere il nostro approccio NIPS 2017: Imparare a correre. Se desideri saperne di più in un ambiente di competizione divertente, dai un'occhiata a NIPS 2018 Competitions o crowdai.org.

Se stai per diventare un esperto di machine learning e desideri approfondire le tue conoscenze nell'apprendimento supervisionato, dai un'occhiata all'analisi video di machine learning: identificazione dei pesci per un divertente esperimento sull'identificazione dei pesci.