Une plongée profonde dans l'apprentissage par renforcement

Plongeons en profondeur dans l'apprentissage par renforcement. Dans cet article, nous aborderons un problème concret avec les bibliothèques modernes telles que TensorFlow, TensorBoard, Keras et OpenAI gym. Vous verrez comment implémenter l'un des algorithmes fondamentaux appelés deep $Q$-learning pour apprendre son fonctionnement interne. En ce qui concerne le matériel, l'ensemble du code fonctionnera sur un PC typique et utilisera tous les cœurs de processeur trouvés (ceci est géré par TensorFlow).

Le problème s'appelle Mountain Car : Une voiture se trouve sur une piste unidimensionnelle, positionnée entre deux montagnes. Le but est de monter la montagne sur la droite (atteindre le drapeau). Cependant, le moteur de la voiture n'est pas assez puissant pour gravir la montagne en un seul passage. Par conséquent, la seule façon de réussir est de faire des allers-retours pour créer une dynamique.

Ce problème a été choisi car il est assez simple de trouver une solution avec un apprentissage par renforcement en quelques minutes sur un seul cœur de processeur. Cependant, il est suffisamment complexe pour être un bon représentant.

Tout d'abord, je vais donner un bref résumé de ce que fait l'apprentissage par renforcement en général. Ensuite, nous couvrirons les termes de base et exprimerons notre problème avec eux. Après cela, je décrirai l'algorithme d'apprentissage $Q$ profond et nous l'implémenterons pour résoudre le problème.

Bases de l'apprentissage par renforcement

L'apprentissage par renforcement dans les mots les plus simples est l'apprentissage par essais et erreurs. Le personnage principal est appelé un "agent", ce qui serait une voiture dans notre problème. L'agent effectue une action dans un environnement et reçoit une nouvelle observation et une récompense pour cette action. Les actions menant à de plus grandes récompenses sont renforcées, d'où le nom. Comme beaucoup d'autres choses en informatique, celle-ci a également été inspirée par l'observation de créatures vivantes.

Les interactions de l'agent avec un environnement sont résumées dans le graphique suivant :

L'agent obtient une observation et une récompense pour l'action effectuée. Ensuite, il fait une autre action et passe à la deuxième étape. L'environnement renvoie maintenant une observation et une récompense (probablement) légèrement différentes. Cela continue jusqu'à ce que l'état terminal soit atteint, signalé par l'envoi de « terminé » à un agent. L'ensemble de la séquence d' observations > actions > prochaines_observations > récompenses est appelé un épisode (ou trajectoire).

Pour en revenir à notre Mountain Car : notre voiture est un mandataire. L'environnement est un monde de boîte noire de montagnes unidimensionnelles. L'action de la voiture se résume à un seul chiffre : s'il est positif, le moteur pousse la voiture vers la droite. S'il est négatif, il pousse la voiture vers la gauche. L'agent perçoit un environnement à travers une observation : la position X et la vitesse de la voiture. Si nous voulons que notre voiture roule au sommet de la montagne, nous définissons la récompense de manière pratique : l'agent obtient -1 à sa récompense pour chaque étape dans laquelle il n'a pas atteint l'objectif. Lorsqu'il atteint l'objectif, l'épisode se termine. Donc, en fait, l'agent est puni pour ne pas être dans une position que nous voulons qu'il soit. Plus vite il l'atteint, mieux c'est pour lui. L'objectif de l'agent est de maximiser la récompense totale, qui est la somme des récompenses d'un épisode. Donc, s'il atteint le point souhaité après, par exemple, 110 pas, il reçoit un rendement total de -110, ce qui serait un excellent résultat pour Mountain Car, car s'il n'atteint pas le but, il est puni de 200 pas. (d'où un rendement de -200).

C'est toute la formulation du problème. Maintenant, nous pouvons le donner aux algorithmes, qui sont déjà assez puissants pour résoudre de tels problèmes en quelques minutes (s'ils sont bien réglés). Il convient de noter que nous ne disons pas à l'agent comment atteindre l'objectif. Nous ne fournissons même pas d'indices (heuristiques). L'agent trouvera un moyen (une politique) de gagner par lui-même.

Configuration de l'environnement

Tout d'abord, copiez l'intégralité du code du didacticiel sur votre disque :

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Maintenant, nous devons installer les packages Python que nous utiliserons. Pour ne pas les installer dans votre espace utilisateur (et risquer des collisions), nous allons le rendre propre et les installer dans l'environnement conda. Si vous n'avez pas installé conda, veuillez suivre https://conda.io/docs/user-guide/install/index.html.

Pour créer notre environnement conda :

 conda create -n tutorial python=3.6.5 -y

Pour l'activer :

 source activate tutorial

Vous devriez voir (tutorial) près de votre invite dans le shell. Cela signifie qu'un environnement conda avec le nom "tutoriel" est actif. À partir de maintenant, toutes les commandes doivent être exécutées dans cet environnement conda.

Maintenant, nous pouvons installer toutes les dépendances dans notre environnement conda hermétique :

 pip install -r requirements.txt

Nous avons terminé l'installation, alors exécutons du code. Nous n'avons pas besoin d'implémenter l'environnement Mountain Car nous-mêmes ; la bibliothèque OpenAI Gym fournit cette implémentation. Voyons un agent aléatoire (un agent qui effectue des actions aléatoires) dans notre environnement :

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

C'est le fichier see.py ; pour l'exécuter, exécutez:

 python see.py

Vous devriez voir une voiture faire des allers-retours aléatoires. Chaque épisode sera composé de 200 étapes ; le rendement total sera de -200.

Maintenant, nous devons remplacer les actions aléatoires par quelque chose de mieux. Il existe de nombreux algorithmes que l'on pourrait utiliser. Pour un tutoriel d'introduction, je pense qu'une approche appelée deep $Q$-learning est un bon choix. Comprendre cette méthode donne une base solide pour apprendre d'autres approches.

Apprentissage $Q$ en profondeur

L'algorithme que nous allons utiliser a été décrit pour la première fois en 2013 par Mnih et al. en jouant à Atari avec Deep Reinforcement Learning et peaufiné deux ans plus tard en contrôle au niveau humain grâce à Deep Reinforcement Learning. De nombreux autres travaux s'appuient sur ces résultats, notamment l'algorithme de pointe actuel Rainbow (2017) :

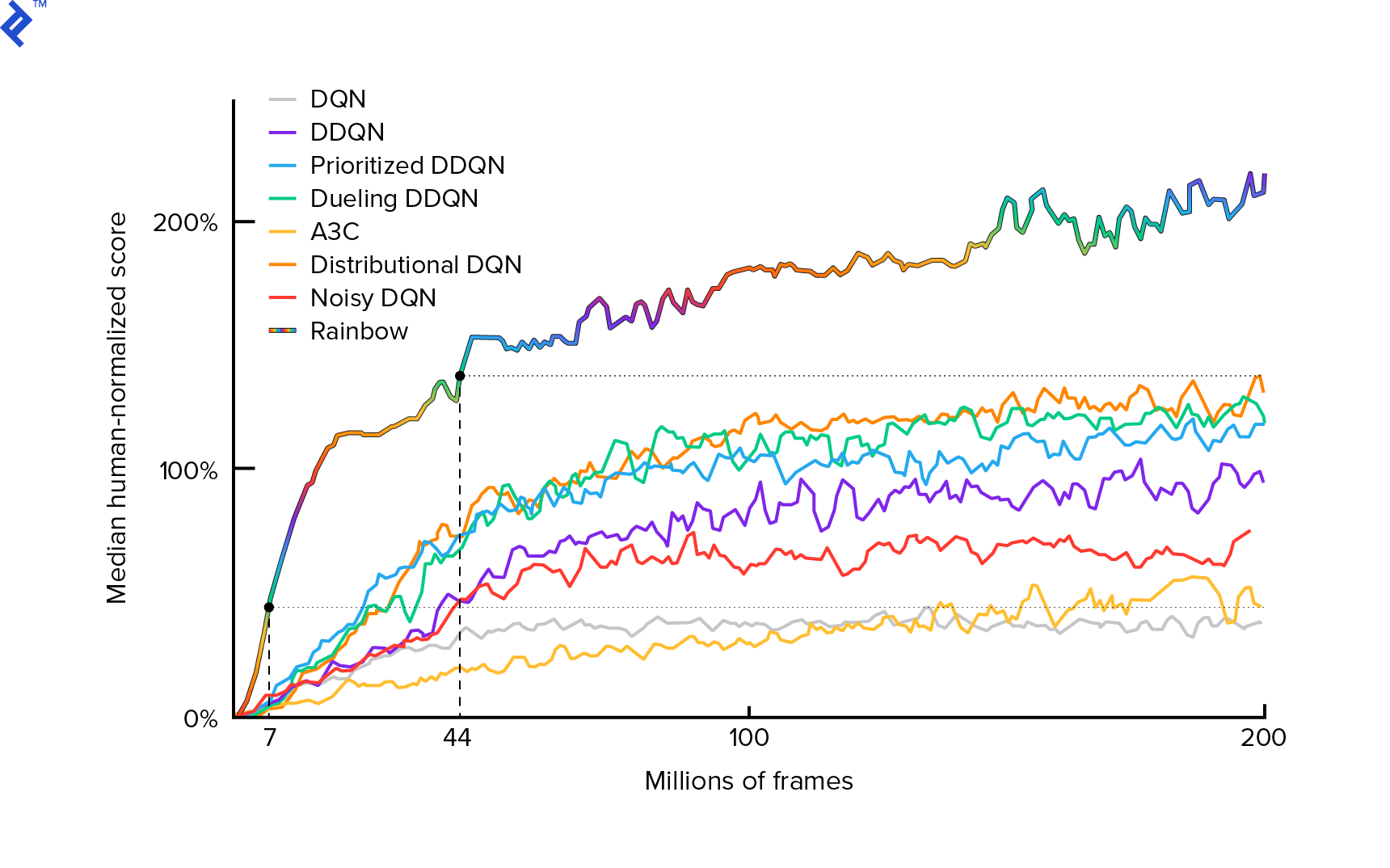
Rainbow atteint des performances surhumaines sur de nombreux jeux Atari 2600. Nous nous concentrerons sur la version de base de DQN, avec un nombre d'améliorations supplémentaires aussi réduit que possible, afin de maintenir ce didacticiel à une taille raisonnable.

Une politique, généralement notée $π(s)$, est une fonction renvoyant des probabilités d'entreprendre des actions individuelles dans un état donné $s$. Ainsi, par exemple, une politique Mountain Car aléatoire revient pour n'importe quel état : 50 % à gauche, 50 % à droite. Pendant le jeu, nous échantillonnons à partir de cette politique (distribution) pour obtenir des actions réelles.

$Q$-learning (Q est pour Qualité) fait référence à la fonction action-valeur notée $Q_π(s, a)$. Il renvoie le rendement total d'un état donné $s$, en choisissant l'action $a$, en suivant une politique concrète $π$. Le rendement total est la somme de toutes les récompenses d'un épisode (trajectoire).

Si nous connaissions la fonction $Q$ optimale, notée $Q^*$, nous pourrions facilement résoudre le jeu. Nous suivrions simplement les actions avec la valeur la plus élevée de $Q^*$, c'est-à-dire le rendement attendu le plus élevé. Cela garantit que nous atteindrons le rendement le plus élevé possible.

Cependant, nous ne connaissons souvent pas $Q^*$. Dans de tels cas, nous pouvons l'approximer – ou « l'apprendre » – à partir des interactions avec l'environnement. Il s'agit de la partie "$Q$-learning" dans le nom. Il y a aussi le mot « profond » parce que, pour approximer cette fonction, nous allons utiliser des réseaux de neurones profonds, qui sont des approximateurs universels de fonctions. Les réseaux de neurones profonds qui se rapprochent des valeurs $Q$ ont été nommés Deep Q-Networks (DQN). Dans des environnements simples (avec le nombre d'états en mémoire), on pourrait simplement utiliser une table au lieu d'un réseau de neurones pour représenter la fonction $Q$, auquel cas elle serait nommée "apprentissage tabulaire $Q$".

Donc, notre objectif est maintenant d'approximer la fonction $Q^*$. Nous utiliserons l'équation de Bellman :

\[Q(s, une) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ est l'état après $s$. $γ$ (gamma), typiquement 0,99, est un facteur d'actualisation (c'est un hyperparamètre). Il accorde un poids moindre aux récompenses futures (car elles sont moins certaines que les récompenses immédiates avec notre $Q$ imparfait). L'équation de Bellman est au cœur de l'apprentissage $Q$ profond. Il indique que la valeur $Q$ pour un état et une action donnés est une récompense $r$ reçue après avoir effectué l'action $a$ plus la valeur $Q$ la plus élevée pour l'état dans lequel nous atterrissons $s'$. Le plus élevé est en un sens que nous choisissons une action $a'$, qui conduit au rendement total le plus élevé de $s'$.

Avec l'équation de Bellman, nous pouvons utiliser l'apprentissage supervisé pour approximer $Q^*$. La fonction $Q$ sera représentée (paramétrée) par des poids de réseau de neurones notés $θ$ (thêta). Une implémentation simple prendrait un état et une action comme entrée et sortie du réseau la valeur Q. L'inefficacité est que si nous voulons connaître les valeurs $Q$ pour toutes les actions dans un état donné, nous devons appeler $Q$ autant de fois qu'il y a d'actions. Il y a une bien meilleure façon : de ne prendre que l'état comme valeur d'entrée et de sortie $Q$ pour toutes les actions possibles. Grâce à cela, nous pouvons obtenir des valeurs $Q$ pour toutes les actions en une seule passe avant.

Nous commençons à entraîner le réseau $Q$ avec des poids aléatoires. De l'environnement, nous obtenons de nombreuses transitions (ou « expériences »). Ce sont des tuples de (état, action, état suivant, récompense) ou, en bref, ($s$, $a$, $s'$, $r$). Nous stockons des milliers d'entre eux dans un tampon en anneau appelé "replay d'expérience". Ensuite, nous prélevons des expériences à partir de ce tampon avec le désir que l'équation de Bellman tienne pour elles. Nous aurions pu sauter le tampon et appliquer les expériences une par une (c'est ce qu'on appelle « en ligne » ou « sur politique ») ; le problème est que les expériences ultérieures sont fortement corrélées les unes aux autres et que DQN s'entraîne mal lorsque cela se produit. C'est pourquoi la relecture de l'expérience a été introduite (une approche « hors ligne », « hors politique ») pour briser cette corrélation de données. Le code de notre implémentation de tampon circulaire la plus simple se trouve dans le fichier replay_buffer.py , je vous encourage à le lire.

Au début, puisque nos poids de réseau de neurones étaient aléatoires, la valeur du côté gauche de l'équation de Bellman sera loin du côté droit. La différence au carré sera notre fonction de perte. Nous allons minimiser la fonction de perte en changeant les poids du réseau de neurones $θ$. Écrivons notre fonction de perte :

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

C'est une équation de Bellman réécrite. Disons que nous avons échantillonné une expérience ($s$, gauche, $s'$, -1) à partir de la relecture de l'expérience Mountain Car. Nous faisons un passage vers l'avant à travers notre réseau $Q$ avec l'état $s$ et pour l'action à gauche, cela nous donne -120, par exemple. Donc, $Q(s, \textrm{gauche}) = -120$. Ensuite, nous envoyons $s'$ au réseau, ce qui nous donne, par exemple, -130 pour la gauche et -122 pour la droite. Il est donc clair que la meilleure action pour $s'$ est la bonne, donc $\textrm{max}_{a'}Q(s', a') = -122$. Nous savons $r$, c'est la vraie récompense, qui était -1. Donc, notre prédiction de réseau $Q$ était légèrement fausse, car $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Nous propageons donc l'erreur en arrière et corrigeons légèrement les poids $θ$. Si nous devions recalculer la perte pour la même expérience, elle serait maintenant inférieure.

Une observation importante avant de passer au code. Remarquons que, pour mettre à jour notre DQN, nous allons faire deux passes avant sur DQN… lui-même. Cela conduit souvent à un apprentissage instable. Pour atténuer cela, pour la prédiction de l'état suivant $Q$, nous n'utilisons pas le même DQN. Nous en utilisons une version plus ancienne, qui dans le code s'appelle target_model (au lieu de model , étant le DQN principal). Grâce à cela, nous avons un objectif stable. Nous mettons à jour target_model en le définissant sur des poids de model toutes les 1000 étapes. Mais le model mis à jour à chaque étape.

Regardons le code créant le modèle DQN :

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Premièrement, la fonction prend les dimensions de l'espace d'action et d'observation de l'environnement OpenAI Gym donné. Il faut savoir, par exemple, combien de sorties aura notre réseau. Il doit être égal au nombre d'actions. Les actions sont codées à chaud :

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Ainsi (par exemple) gauche sera [1, 0] et droite sera [0, 1].

Nous pouvons voir que les observations sont passées en entrée. Nous passons également action_mask comme deuxième entrée. Pourquoi? Lors du calcul de $Q(s,a)$, nous n'avons besoin de connaître la valeur de $Q$ que pour une action donnée, pas pour toutes. action_mask contient 1 pour les actions que nous voulons passer à la sortie DQN. Si action_mask a 0 pour une action, alors la valeur $Q$ correspondante sera mise à zéro sur la sortie. La couche filtered_output fait cela. Si nous voulons toutes les valeurs $Q$ (pour le calcul max), nous pouvons simplement passer toutes les valeurs.

Le code utilise keras.layers.Dense pour définir une couche entièrement connectée. Keras est une bibliothèque Python pour une abstraction de niveau supérieur en plus de TensorFlow. Sous le capot, Keras crée un graphique TensorFlow, avec des biais, une initialisation de poids appropriée et d'autres éléments de bas niveau. Nous aurions pu simplement utiliser TensorFlow brut pour définir le graphique, mais ce ne sera pas une ligne.

Ainsi, les observations sont transmises à la première couche cachée, avec des activations ReLU (unité linéaire rectifiée). ReLU(x) n'est qu'une fonction $\textrm{max}(0, x)$. Cette couche est entièrement connectée à une seconde identique, hidden_2 . La couche de sortie ramène le nombre de neurones au nombre d'actions. Au final, nous avons filtered_output , qui multiplie simplement la sortie avec action_mask .

Pour trouver les poids $θ$, nous utiliserons un optimiseur nommé "Adam" avec une perte d'erreur quadratique moyenne.

Ayant un modèle, nous pouvons l'utiliser pour prédire les valeurs $Q$ pour des observations d'état données :

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Nous voulons des valeurs $Q$ pour toutes les actions, donc action_mask est un vecteur de uns.

Pour faire la formation proprement dite, nous utiliserons fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Le lot contient BATCH_SIZE expériences. next_q_values ​​est $Q(s, a)$. q_values ​​est $r + γ \space \textrm{max}_{a'}Q(s', a')$ de l'équation de Bellman. Les actions que nous avons prises sont codées à chaud et transmises en tant que action_mask d'action à l'entrée lors de l'appel model.fit() . $y$ est une lettre commune pour une « cible » dans l'apprentissage supervisé. Ici, nous passons les q_values ​​. Je fais q_values[:. None] q_values[:. None] pour augmenter la dimension du tableau car elle doit correspondre à la dimension du tableau one_hot_actions . C'est ce qu'on appelle la notation de tranche si vous souhaitez en savoir plus à ce sujet.

Nous renvoyons la perte pour l'enregistrer dans le fichier journal TensorBoard et la visualiser plus tard. Il y a beaucoup d'autres choses que nous surveillerons : combien de pas par seconde nous faisons, utilisation totale de la RAM, quel est le retour moyen des épisodes, etc. Voyons ces tracés.

Fonctionnement

Pour visualiser le fichier journal TensorBoard, nous devons d'abord en avoir un. Alors exécutons simplement la formation :

 python run.py

Cela imprimera d'abord le résumé de notre modèle. Ensuite, il créera un répertoire de journaux avec la date actuelle et commencera la formation. Toutes les 2 000 pas, une ligne de connexion similaire à celle-ci sera imprimée :

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Tous les 20 000, nous évaluerons notre modèle sur 10 000 pas :

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Après 677 épisodes et 120 000 pas, le retour moyen des épisodes est passé de -200 à -136,75 ! C'est certainement un apprentissage. Quelle avg_max_q_value est-ce que je laisse comme un bon exercice au lecteur. Mais c'est une statistique très utile à regarder pendant l'entraînement.

Après 200 000 pas, notre entraînement est terminé. Sur mon processeur à quatre cœurs, cela prend environ 20 minutes. Nous pouvons regarder dans le répertoire date-log , par exemple, 06-07-18-39-log . Il y aura quatre fichiers de modèle avec l'extension .h5 . Il s'agit d'un instantané des poids du graphique TensorFlow, nous les enregistrons toutes les 50 000 étapes pour examiner ultérieurement la politique que nous avons apprise. Pour le voir :

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Pour voir les autres drapeaux possibles : python run.py --help .

Maintenant, la voiture fait un bien meilleur travail pour atteindre l'objectif souhaité. Dans le répertoire date-log , il y a aussi le fichier events.out.* . C'est le fichier dans lequel TensorBoard stocke ses données. Nous y écrivons en utilisant le TensorBoardLogger le plus simple défini dans loggers.py. Pour afficher le fichier d'événements, nous devons exécuter le serveur TensorBoard local :

 tensorboard --logdir=.

--logdir pointe simplement vers le répertoire dans lequel se trouvent les répertoires de journalisation des dates, dans notre cas, ce sera le répertoire courant, donc . . TensorBoard imprime l'URL à laquelle il écoute. Si vous ouvrez http://127.0.0.1:6006, vous devriez voir huit tracés similaires à ceux-ci :

Emballer

train() fait toute la formation. Nous créons d'abord le modèle et rejouons le tampon. Ensuite, dans une boucle très similaire à celle de see.py , nous interagissons avec l'environnement et stockons les expériences dans le tampon. Ce qui est important, c'est que nous suivions une politique gourmande d'epsilon. Nous pourrions toujours choisir la meilleure action selon la fonction $Q$ ; cependant, cela décourage l'exploration, ce qui nuit aux performances globales. Donc, pour appliquer l'exploration avec probabilité epsilon, nous effectuons des actions aléatoires :

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon a été fixé à 1 %. Après 2000 expériences, le replay se remplit suffisamment pour commencer l'entraînement. Nous le faisons en appelant fit_batch() avec un lot aléatoire d'expériences échantillonnées à partir du tampon de relecture :

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Toutes les 20 000 étapes, nous évaluons et enregistrons les résultats (l'évaluation est avec epsilon = 0 , politique totalement gourmande) :

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

L'ensemble du code est d'environ 300 lignes, et run.py contient environ 250 des plus importantes.

On peut remarquer qu'il y a beaucoup d'hyperparamètres :

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Et ce n'est même pas tout. Il existe également une architecture réseau - nous avons utilisé deux couches cachées avec 32 neurones, des activations ReLU et un optimiseur Adam, mais il existe de nombreuses autres options. Même de petits changements peuvent avoir un impact énorme sur la formation. Beaucoup de temps peut être consacré au réglage des hyperparamètres. Lors d'une récente compétition OpenAI, un candidat à la deuxième place a découvert qu'il était possible de presque doubler le score de Rainbow après le réglage des hyperparamètres. Naturellement, il faut se rappeler qu'il est facile de se suradapter. Actuellement, les algorithmes de renforcement ont du mal à transférer des connaissances vers des environnements similaires. Notre Mountain Car ne se généralise pas à tous les types de montagne pour le moment. Vous pouvez réellement modifier l'environnement OpenAI Gym et voir jusqu'où l'agent peut généraliser.

Un autre exercice consistera à trouver un meilleur ensemble d'hyperparamètres que le mien. C'est tout à fait possible. Cependant, une course d'entraînement ne suffira pas pour juger si votre changement est une amélioration. Il y a généralement une grande différence entre les courses d'entraînement; l'écart est grand. Vous auriez besoin de plusieurs exécutions pour déterminer que quelque chose est mieux. Si vous souhaitez en savoir plus sur un sujet aussi important que la reproductibilité, je vous encourage à lire Deep Reinforcement Learning that Matters. Au lieu de régler à la main, nous pouvons automatiser ce processus dans une certaine mesure, si nous sommes prêts à consacrer plus de puissance de calcul au problème. Une approche simple consiste à préparer une gamme prometteuse de valeurs pour certains hyperparamètres et à exécuter une recherche de grille (vérifiant leurs combinaisons), avec des entraînements exécutés en parallèle. La parallélisation elle-même est un sujet important en soi car elle est cruciale pour des performances élevées.

Deep $Q$-learning représente une grande famille d'algorithmes d'apprentissage par renforcement qui utilisent l'itération de valeur. Nous avons essayé d'approximer la fonction $Q$, et nous l'avons simplement utilisée de manière gourmande la plupart du temps. Il existe une autre famille qui utilise l'itération de politique. Ils ne se concentrent pas sur l'approximation de la fonction $Q$, mais sur la recherche directe de la politique optimale $π^*$. Pour voir où se situe l'itération de valeur dans le paysage des algorithmes d'apprentissage par renforcement :

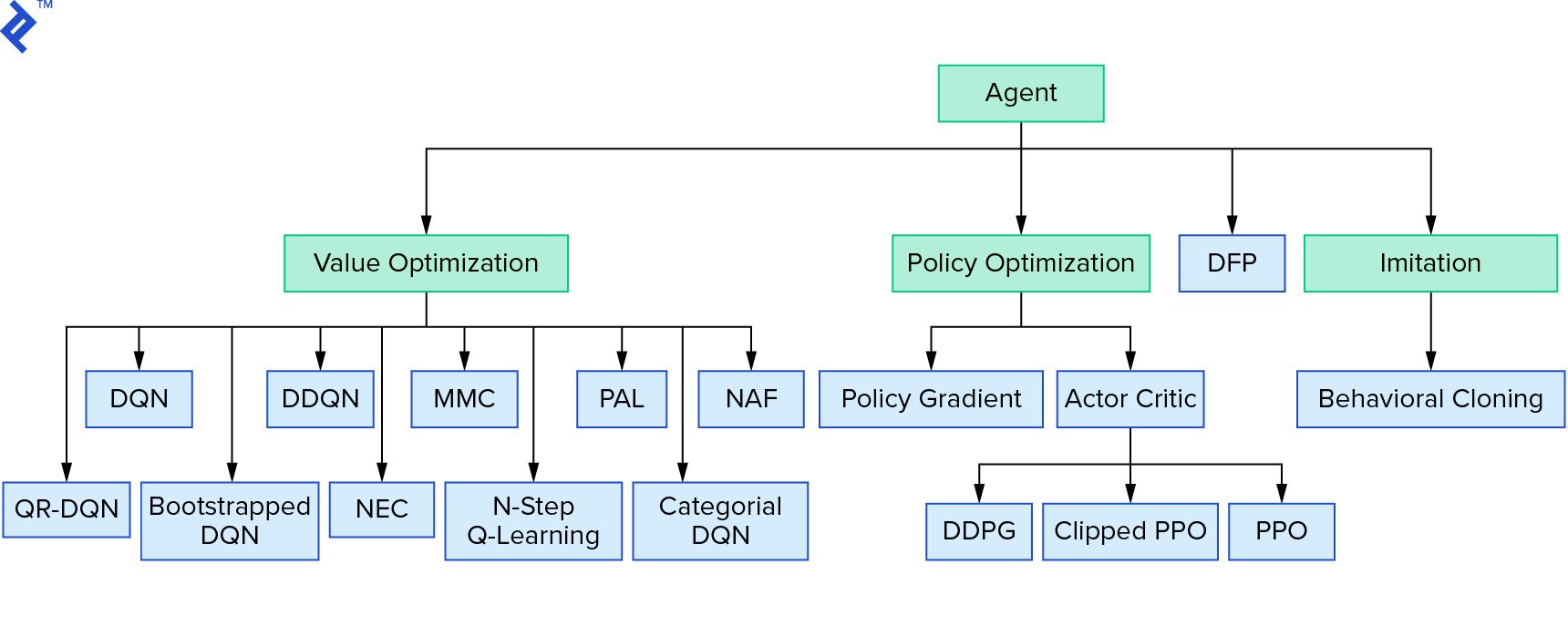
Vous pensez peut-être que l'apprentissage par renforcement profond semble fragile. Vous aurez raison; il y a beaucoup de problèmes. Vous pouvez vous référer à L'apprentissage par renforcement en profondeur ne fonctionne pas encore et L'apprentissage par renforcement n'a jamais fonctionné, et « en profondeur » n'a aidé qu'un peu.

Ceci conclut le didacticiel. Nous avons implémenté notre propre DQN de base à des fins d'apprentissage. Un code très similaire peut être utilisé pour obtenir de bonnes performances dans certains des jeux Atari. Dans les applications pratiques, on prend souvent des implémentations testées et performantes, par exemple, une des lignes de base OpenAI. Si vous souhaitez voir à quels défis on peut être confronté lorsqu'on essaie d'appliquer l'apprentissage par renforcement profond dans un environnement plus complexe, vous pouvez lire Notre approche NIPS 2017 : Apprendre à courir. Si vous souhaitez en savoir plus dans un environnement de compétition amusant, consultez NIPS 2018 Competitions ou crowdai.org.

Si vous êtes sur le point de devenir un expert en apprentissage automatique et que vous souhaitez approfondir vos connaissances en apprentissage supervisé, consultez l'analyse vidéo d'apprentissage automatique : identifier les poissons pour une expérience amusante sur l'identification des poissons.