強化学習の詳細
公開: 2022-03-11強化学習について深く掘り下げてみましょう。 この記事では、TensorFlow、TensorBoard、Keras、OpenAIジムなどの最新のライブラリに関する具体的な問題に取り組みます。 ディープ$Q$と呼ばれる基本的なアルゴリズムの1つを実装する方法を学びます-その内部の仕組みを学ぶために、学習します。 ハードウェアに関しては、コード全体が一般的なPCで動作し、見つかったすべてのCPUコアを使用します(これはTensorFlowによってそのまま処理されます)。
この問題はマウンテンカーと呼ばれます。車は2つの山の間に配置された1次元のトラック上にあります。 目標は、右側の山をドライブすることです(旗に到達します)。 しかし、車のエンジンは、1回のパスで山を登るのに十分な強度ではありません。 したがって、成功する唯一の方法は、勢いを増すために前後に運転することです。
この問題が選択されたのは、単一のCPUコアで強化学習を数分で実行できるソリューションを見つけるのが簡単だからです。 しかし、それは良い代表となるのに十分複雑です。
まず、強化学習が一般的に行うことの概要を説明します。 次に、基本的な用語を取り上げ、問題を表現します。 その後、深い$ Q $学習アルゴリズムについて説明し、問題を解決するためにそれを実装します。
強化学習の基本
最も簡単な言葉での強化学習は、試行錯誤による学習です。 主人公は「エージェント」と呼ばれ、私たちの問題では車になります。 エージェントは環境内でアクションを実行し、そのアクションに対する新しい観察と報酬が返されます。 より大きな報酬につながるアクションが強化されているため、この名前が付けられています。 コンピュータサイエンスの他の多くのものと同様に、これも生き物を観察することに触発されました。
エージェントと環境との相互作用は、次のグラフに要約されています。
エージェントは、実行されたアクションに対して観察と報酬を受け取ります。 次に、別のアクションを実行し、ステップ2を実行します。 環境は現在、(おそらく)わずかに異なる観察と報酬を返します。 これは、エージェントに「完了」を送信することによって通知され、ターミナル状態に達するまで続きます。 観察>アクション>next_observations>報酬のシーケンス全体は、エピソード(または軌道)と呼ばれます。
マウンテンカーに戻ります。私たちの車はエージェントです。 環境は一次元の山々のブラックボックスの世界です。 車の動作は1つの数字に要約されます。正の場合、エンジンが車を右に押します。 負の場合、車を左に押します。 エージェントは、車のX位置と速度を観察することで環境を認識します。 車を山の頂上で運転したい場合は、便利な方法で報酬を定義します。エージェントは、目標に到達していないすべてのステップで報酬を-1にします。 ゴールに到達するとエピソードは終了します。 したがって、実際には、エージェントは、私たちが望む位置にいないことで罰せられます。 彼がそれに到達するのが早いほど、彼にとっては良いことです。 エージェントの目標は、1つのエピソードからの報酬の合計である合計報酬を最大化することです。 したがって、たとえば110ステップ後に目的のポイントに到達すると、合計で-110のリターンが得られます。これは、マウンテンカーにとっては素晴らしい結果です。これは、目標に到達しない場合、200ステップで罰せられるためです。 (したがって、-200のリターン)。
これが問題の定式化全体です。 これで、アルゴリズムにそれを与えることができます。アルゴリズムは、このような問題を数分で解決するのに十分強力です(十分に調整されている場合)。 目標を達成する方法をエージェントに教えていないことは注目に値します。 ヒント(ヒューリスティック)も提供していません。 エージェントは自分で勝つ方法(ポリシー)を見つけます。
環境の設定
まず、チュートリアルコード全体をディスクにコピーします。
git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial次に、使用するPythonパッケージをインストールする必要があります。 それらをユーザースペースにインストールしないように(そして衝突のリスクを冒さないように)、クリーンにしてconda環境にインストールします。 condaをインストールしていない場合は、https://conda.io/docs/user-guide/install/index.htmlに従ってください。
conda環境を作成するには:
conda create -n tutorial python=3.6.5 -yそれをアクティブにするには:
source activate tutorial シェルのプロンプトの近くに(tutorial)が表示されます。 これは、「tutorial」という名前のコンダ環境がアクティブであることを意味します。 今後は、すべてのコマンドをそのconda環境内で実行する必要があります。
これで、すべての依存関係を気密コンダ環境にインストールできます。
pip install -r requirements.txtインストールが完了したので、コードを実行してみましょう。 MountainCar環境を自分で実装する必要はありません。 OpenAIGymライブラリはその実装を提供します。 私たちの環境でランダムエージェント(ランダムなアクションを実行するエージェント)を見てみましょう:
import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render() これはsee.pyファイルです。 それを実行するには、以下を実行します。
python see.py車がランダムに前後に移動しているのが見えるはずです。 各エピソードは200ステップで構成されます。 トータルリターンは-200になります。
次に、ランダムアクションをより良いものに置き換える必要があります。 使用できるアルゴリズムはたくさんあります。 入門チュートリアルの場合、ディープ$Q$学習と呼ばれるアプローチが適していると思います。 その方法を理解することは、他のアプローチを学ぶための確固たる基盤を提供します。
深い$Q$-学習
私たちが使用するアルゴリズムは、2013年にMnihらによって最初に説明されました。 深層強化学習でアタリをプレイし、2年後に深層強化学習による人間レベルの制御を磨きました。 現在の最先端のアルゴリズムRainbow(2017)を含む、他の多くの作品がこれらの結果に基づいて構築されています。
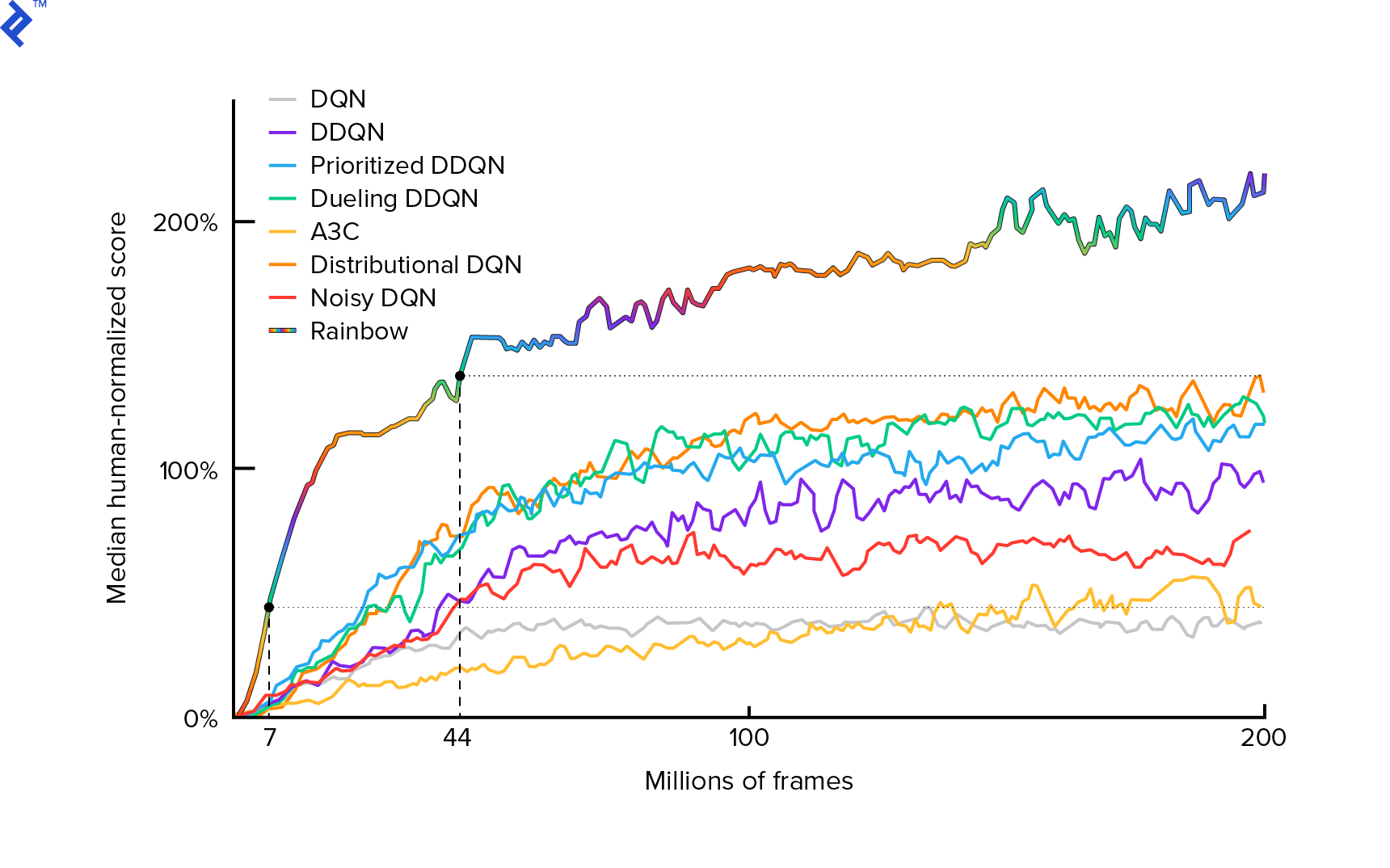
Rainbowは、多くのAtari2600ゲームで超人的なパフォーマンスを実現しています。 このチュートリアルを妥当なサイズに保つために、可能な限り少数の追加の改善を加えた、基本的なDQNバージョンに焦点を当てます。
ポリシーは、通常$π(s)$で表され、特定の状態$s$で個々のアクションを実行する確率を返す関数です。 したがって、たとえば、ランダムなMountain Carポリシーは、任意の状態に対して返されます:左50%、右50%。 ゲームプレイ中に、実際のアクションを取得するために、そのポリシー(配布)からサンプリングします。
$ Q $ -learning(Qは品質を表す)は、$Q_π(s、a)$で表されるアクション値関数を指します。 具体的なポリシー$π$に従って、アクション$ a $を選択し、特定の状態$s$からのトータルリターンを返します。 トータルリターンは、1つのエピソード(軌跡)のすべての報酬の合計です。
$ Q ^*$で表される最適な$Q$関数がわかれば、ゲームを簡単に解くことができます。 $ Q ^ * $の値が最も高い、つまり期待収益が最も高いアクションに従うだけです。 これにより、可能な限り最高の収益が得られることが保証されます。
ただし、$ Q ^*$がわからないことがよくあります。 このような場合、環境との相互作用から概算、つまり「学習」することができます。 これは、名前の「$Q$-learning」の部分です。 その関数を近似するために、普遍関数近似器であるディープニューラルネットワークを使用するため、「ディープ」という単語も含まれています。 $ Q $値を概算するディープニューラルネットワークは、Deep Q-Networks(DQN)と名付けられました。 単純な環境(メモリに収まる状態の数)では、ニューラルネットの代わりにテーブルを使用して$ Q $関数を表すことができます。この場合、「表形式の$Q$学習」という名前になります。
したがって、ここでの目標は、$ Q ^*$関数を近似することです。 ベルマン方程式を使用します。
\ [Q(s、a)=r+γ\space\ textrm {max} _ {a'} Q(s'、a')\]$ s'$は、$s$の後の状態です。 $γ$(ガンマ)、通常は0.99は、割引係数です(ハイパーパラメーターです)。 それは将来の報酬に小さな重みを置きます(それらは私たちの不完全な$ Q $による即時の報酬よりも確実性が低いためです)。 ベルマン方程式は、深い$Q$学習の中心です。 これは、特定の州とアクションの$ Q $値は、アクション$a$を実行した後に受け取った報酬$r$に、$s'$に着陸した州の最高の$Q$値を加えたものであると述べています。 最も高いのは、アクション$ a'$を選択しているという意味で、これは$s'$からの最大のトータルリターンにつながります。
ベルマン方程式を使用すると、教師あり学習を使用して$ Q ^*$を近似できます。 $ Q $関数は、$θ$(シータ)として示されるニューラルネットワークの重みによって表されます(パラメーター化されます)。 単純な実装では、ネットワークがQ値を入力および出力するときに、状態とアクションを実行します。 非効率なのは、特定の状態のすべてのアクションの$ Q $値を知りたい場合、アクションの数だけ$Q$を呼び出す必要があることです。 はるかに優れた方法があります。状態のみを入力として受け取り、すべての可能なアクションの$Q$値を出力することです。 そのおかげで、1回のフォワードパスですべてのアクションの$Q$値を取得できます。
ランダムな重みで$Q$ネットワークのトレーニングを開始します。 環境から、私たちは多くの移行(または「経験」)を取得します。 これらは、(状態、アクション、次の状態、報酬)、つまり($ s $、$ a $、$ s'$、$ r $)のタプルです。 何千ものそれらを「エクスペリエンスリプレイ」と呼ばれるリングバッファに保存します。 次に、ベルマン方程式がそれらに当てはまるという願望を持って、そのバッファーから経験をサンプリングします。 バッファをスキップして、エクスペリエンスを1つずつ適用することもできます(これは「オンライン」または「オンポリシー」と呼ばれます)。 問題は、その後の経験が互いに高度に相関しており、これが発生した場合、DQNのトレーニングが不十分になることです。 そのため、このデータの相関関係を解消するために、エクスペリエンスのリプレイが導入されました(「オフライン」、「オフポリシー」アプローチ)。 最も単純なリングバッファ実装のコードは、 replay_buffer.pyファイルにあります。お読みになることをお勧めします。
最初は、ニューラルネットワークの重みがランダムであったため、ベルマン方程式の左辺の値は右辺から遠くなります。 二乗の差が損失関数になります。 ニューラルネットワークの重み$θ$を変更することにより、損失関数を最小化します。 損失関数を書き留めましょう。
\ [L(θ)= [Q(s、a)--r--γ\ space \ textrm {max} _ {a'} Q(s'、a')] ^ 2 \]これは、書き直されたベルマン方程式です。 Mountain Carエクスペリエンスリプレイからエクスペリエンス($ s $、左、$ s'$、-1)をサンプリングしたとしましょう。 たとえば、状態が$s$の$Q$ネットワークを介してフォワードパスを実行し、アクションが残っている場合は-120になります。 したがって、$ Q(s、\ textrm {left})=-120$です。 次に、$ s'$をネットワークにフィードします。これにより、たとえば、左が-130、右が-122になります。 したがって、明らかに$ s'$の最良のアクションは正しいので、$ \ textrm {max} _ {a'} Q(s'、a')=-122$です。 $ r $を知っています。これが実際の報酬で、-1でした。 したがって、$ L(θ)=[-120-1+0.99⋅122]^2 =(-0.22 ^ 2)= 0.0484 $であるため、$Q$ネットワークの予測はわずかに間違っていました。 したがって、エラーを逆伝播し、重み$θ$をわずかに修正します。 同じ経験で損失を再度計算すると、損失は低くなります。
コードに進む前の重要な観察事項の1つ。 DQNを更新するために、DQN自体で2つのフォワードパスを実行することに注意してください。 これはしばしば不安定な学習につながります。 これを軽減するために、次の状態の$ Q $予測では、同じDQNを使用しません。 コードではtarget_modelと呼ばれる古いバージョンを使用します( modelではなく、メインのDQNです)。 そのおかげで、安定した目標を掲げています。 1000ステップごとにmodelの重みに設定することでtarget_modelを更新します。 ただし、 modelはすべてのステップで更新されます。
DQNモデルを作成するコードを見てみましょう。
def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return modelまず、この関数は、指定されたOpenAIGym環境からアクションと観測空間の次元を取得します。 たとえば、ネットワークの出力数を知る必要があります。 アクションの数と同じである必要があります。 アクションは1つのホットエンコードされます:
def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hotしたがって、(たとえば)左は[1、0]になり、右は[0、1]になります。

観測値が入力として渡されていることがわかります。 また、2番目の入力としてaction_maskを渡します。 なんで? $ Q(s、a)$を計算するときは、すべてではなく、特定の1つのアクションの$Q$値のみを知る必要があります。 action_maskには、DQN出力に渡すアクションの1が含まれています。 あるアクションのaction_maskが0の場合、対応する$Q$-valueは出力でゼロになります。 filtered_outputレイヤーがそれを行っています。 すべての$Q$値(最大計算用)が必要な場合は、すべての値を渡すことができます。
コードはkeras.layers.Denseを使用して、完全に接続されたレイヤーを定義します。 Kerasは、TensorFlowに加えて高レベルの抽象化を行うためのPythonライブラリです。 内部的には、Kerasはバイアス、適切な重みの初期化、およびその他の低レベルのものを使用してTensorFlowグラフを作成します。 生のTensorFlowを使用してグラフを定義することもできますが、ワンライナーにはなりません。
したがって、観測値は、ReLU(正規化線形ユニット)のアクティブ化を使用して、最初の隠れ層に渡されます。 ReLU(x)は単なる$ \ textrm {max}(0、x)$関数です。 そのレイヤーは、2番目の同一のhidden_2 2と完全に接続されています。 出力層は、ニューロンの数をアクションの数に減らします。 最後に、 filtered_outputがあります。これは、出力にaction_maskを乗算するだけです。
$θ$の重みを見つけるために、平均二乗誤差損失を持つ「Adam」という名前のオプティマイザーを使用します。
モデルがあれば、それを使用して、特定の状態の観測値の$Q$値を予測できます。
def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask]) すべてのアクションに$Q$値が必要なので、 action_maskは1のベクトルです。
実際のトレーニングを行うには、 fit_batch()を使用します。
def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0] バッチには、 BATCH_SIZEエクスペリエンスが含まれています。 next_q_valuesは$Q(s、a)$です。 q_valuesは、ベルマン方程式からの$r+γ\space\ textrm {max} _ {a'} Q(s'、a')$です。 実行したアクションは、1つのホットエンコードされ、 model.fit()を呼び出すときにaction_maskとして入力に渡されます。 $ y $は、教師あり学習の「ターゲット」の一般的な文字です。 ここでは、 q_valuesを渡します。 q_values[:. None] q_values[:. None] one_hot_actions配列の次元に対応する必要があるため、配列の次元を増やします。 詳細を知りたい場合は、これをスライス表記と呼びます。
損失を返し、TensorBoardログファイルに保存して後で視覚化します。 監視するものは他にもたくさんあります。1秒あたりの歩数、合計RAM使用量、平均エピソードリターンなどです。これらのプロットを見てみましょう。
ランニング
TensorBoardログファイルを視覚化するには、最初に1つ必要です。 それでは、トレーニングを実行してみましょう。
python run.pyこれにより、最初にモデルの概要が印刷されます。 次に、現在の日付のログディレクトリを作成し、トレーニングを開始します。 2000ステップごとに、次のようなログラインが出力されます。
episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM20,000ごとに、10,000ステップでモデルを評価します。
Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004 677エピソードと120,000ステップの後、平均エピソードリターンは-200から-136.75に向上しました! それは間違いなく学習しています。 avg_max_q_valueは、読者に良い演習として残しています。 しかし、トレーニング中に確認することは非常に有用な統計です。
200,000ステップ後、トレーニングが完了します。 私の4コアCPUでは、約20分かかります。 date-logディレクトリの内部を見ることができます(例: 06-07-18-39-log )。 拡張子が.h5のモデルファイルが4つあります。 これはTensorFlowグラフの重みのスナップショットです。後で学習したポリシーを確認するために、50,000ステップごとにそれらを保存します。 表示するには:
python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view 他の可能なフラグを確認するには: python run.py --help 。
今、車は目的の目標を達成するためにはるかに優れた仕事をしています。 date-logディレクトリには、 events.out.*ファイルもあります。 これは、TensorBoardがデータを保存するファイルです。 TensorBoardLoggerで定義されている最も単純なTensorBoardLoggerを使用して書き込みloggers.py. イベントファイルを表示するには、ローカルのTensorBoardサーバーを実行する必要があります。
tensorboard --logdir=. --logdirは、date-logディレクトリが存在するディレクトリを指しているだけです。この場合、これが現在のディレクトリになるため、 . 。 TensorBoardは、リッスンしているURLを出力します。 http://127.0.0.1:6006を開くと、次のような8つのプロットが表示されます。
まとめ
train()はすべてのトレーニングを行います。 最初にモデルを作成し、バッファーを再生します。 次に、 see.pyのループと非常によく似たループで、環境と対話し、エクスペリエンスをバッファーに保存します。 重要なのは、イプシロン欲張りポリシーに従うことです。 $ Q $関数に従って、常に最適なアクションを選択できます。 ただし、それは全体的なパフォーマンスを損なう探索を思いとどまらせます。 したがって、イプシロン確率で探索を実施するために、ランダムなアクションを実行します。
def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action イプシロンは1%に設定されました。 2000回の経験の後、リプレイはトレーニングを開始するのに十分な量になります。 これを行うには、再生バッファーからサンプリングされたエクスペリエンスのランダムなバッチを使用してfit_batch()を呼び出します。
batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch) 20,000ステップごとに、結果を評価してログに記録します(評価はepsilon = 0 、完全に貪欲なポリシーで行われます)。
if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step) コード全体は約300行で、 run.pyには約250の最も重要なコードが含まれています。
多くのハイパーパラメータがあることに気付くでしょう。
DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000そして、それはそれらのすべてではありません。 ネットワークアーキテクチャもあります。32個のニューロンを持つ2つの隠れ層、ReLUアクティベーション、およびAdamオプティマイザーを使用しましたが、他にも多くのオプションがあります。 小さな変更でも、トレーニングに大きな影響を与える可能性があります。 ハイパーパラメータの調整に多くの時間を費やすことができます。 最近のOpenAIコンテストで、2位の競技者は、ハイパーパラメータ調整後にRainbowのスコアをほぼ2倍にすることが可能であることを発見しました。 当然、過剰適合は簡単であることを覚えておく必要があります。 現在、強化アルゴリズムは、同様の環境への知識の伝達に苦労しています。 私たちのマウンテンカーは、現在、すべてのタイプの山に一般化されているわけではありません。 実際にOpenAIGym環境を変更して、エージェントがどこまで一般化できるかを確認できます。
もう1つの演習は、私のものよりも優れたハイパーパラメータのセットを見つけることです。 それは間違いなく可能です。 ただし、1回のトレーニング実行では、変更が改善であるかどうかを判断するのに十分ではありません。 通常、トレーニングの実行には大きな違いがあります。 分散が大きいです。 何かがより良いと判断するには、多くの実行が必要になります。 再現性などの重要なトピックについて詳しく知りたい場合は、重要な深層強化学習を読むことをお勧めします。 手作業で調整する代わりに、問題により多くの計算能力を費やすことをいとわない場合は、このプロセスをある程度自動化することができます。 簡単なアプローチは、いくつかのハイパーパラメータに対して有望な範囲の値を準備し、トレーニングを並行して実行してグリッド検索を実行する(それらの組み合わせをチェックする)ことです。 並列化自体は、高性能にとって非常に重要であるため、それ自体が大きなトピックです。
深い$Q$学習は、値の反復を使用する強化学習アルゴリズムの大きなファミリーを表しています。 $ Q $関数を概算しようとしましたが、ほとんどの場合、貪欲に使用していました。 ポリシーの反復を使用する別のファミリがあります。 彼らは$Q$関数を近似することに焦点を合わせていませんが、最適なポリシー$π^*$を直接見つけることに焦点を合わせています。 値の反復が強化学習アルゴリズムのランドスケープのどこに適合するかを確認するには、次のようにします。
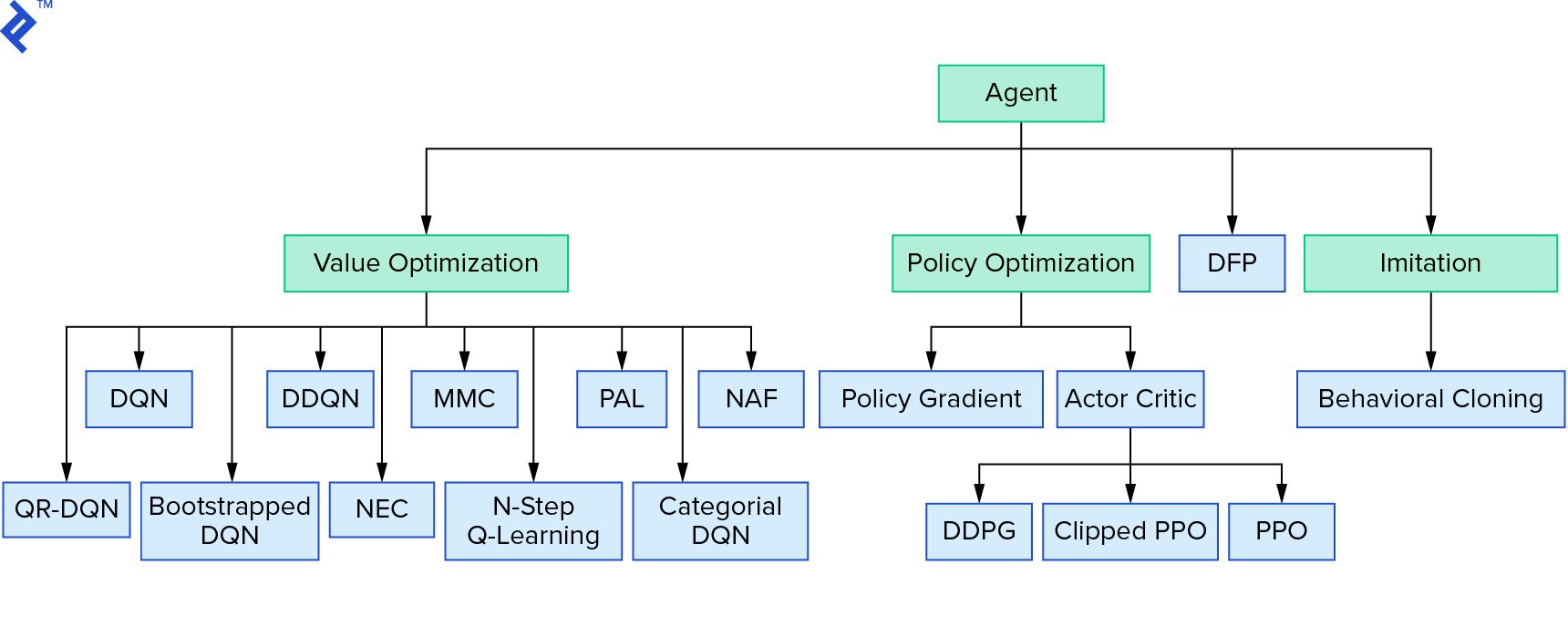
あなたの考えは、深い強化学習がもろく見えるということかもしれません。 あなたは正しいでしょう。 多くの問題があります。 深層強化学習はまだ機能せず、強化学習は機能しなかったことを参照できます。「深層」は少ししか役に立ちませんでした。
これでチュートリアルは終わりです。 学習目的で独自の基本的なDQNを実装しました。 非常によく似たコードを使用して、一部のAtariゲームで優れたパフォーマンスを実現できます。 実際のアプリケーションでは、多くの場合、OpenAIベースラインからの実装など、テスト済みの高性能実装を採用します。 より複雑な環境で深層強化学習を適用しようとするときに直面する可能性のある課題を確認したい場合は、NIPS 2017:LearningtoRunアプローチをお読みください。 楽しい競技環境で詳細を知りたい場合は、NIPS2018競技会またはcrowdai.orgをご覧ください。
機械学習の専門家になる途中で、教師あり学習の知識を深めたい場合は、機械学習ビデオ分析:魚の識別をチェックして、魚の識別に関する楽しい実験を行ってください。
