Um mergulho profundo no aprendizado por reforço

Vamos mergulhar profundamente no aprendizado por reforço. Neste artigo, abordaremos um problema concreto com bibliotecas modernas, como TensorFlow, TensorBoard, Keras e academia OpenAI. Você verá como implementar um dos algoritmos fundamentais chamado deep $Q$-learning para aprender seu funcionamento interno. Em relação ao hardware, todo o código funcionará em um PC típico e usará todos os núcleos de CPU encontrados (isso é tratado imediatamente pelo TensorFlow).

O problema é chamado Mountain Car: Um carro está em uma pista unidimensional, posicionada entre duas montanhas. O objetivo é subir a montanha à direita (alcançar a bandeira). No entanto, o motor do carro não é forte o suficiente para escalar a montanha em uma única passagem. Portanto, a única maneira de ter sucesso é ir e voltar para ganhar impulso.

Esse problema foi escolhido porque é simples o suficiente para encontrar uma solução com aprendizado por reforço em minutos em um único núcleo de CPU. No entanto, é complexo o suficiente para ser um bom representante.

Primeiro, darei um breve resumo do que o aprendizado por reforço faz em geral. Em seguida, abordaremos os termos básicos e expressaremos nosso problema com eles. Depois disso, descreverei o algoritmo de aprendizado profundo $Q$ e o implementaremos para resolver o problema.

Noções básicas de aprendizado por reforço

O aprendizado por reforço nas palavras mais simples é o aprendizado por tentativa e erro. O personagem principal é chamado de “agente”, o que seria um carro em nosso problema. O agente realiza uma ação em um ambiente e recebe de volta uma nova observação e uma recompensa por essa ação. Ações que levam a maiores recompensas são reforçadas, daí o nome. Tal como acontece com muitas outras coisas na ciência da computação, esta também foi inspirada na observação de criaturas vivas.

As interações do agente com um ambiente estão resumidas no gráfico a seguir:

O agente recebe uma observação e recompensa pela ação realizada. Então ele faz outra ação e dá o passo dois. O ambiente agora retorna uma observação e recompensa (provavelmente) ligeiramente diferente. Isso continua até que o estado terminal seja alcançado, sinalizado pelo envio de “concluído” para um agente. Toda a sequência de observações > ações > next_observations > recompensas é chamada de episódio (ou trajetória).

Voltando ao nosso Mountain Car: nosso carro é um agente. O ambiente é um mundo caixa-preta de montanhas unidimensionais. A ação do carro se resume a apenas um número: se positivo, o motor empurra o carro para a direita. Se negativo, empurra o carro para a esquerda. O agente percebe um ambiente através de uma observação: a posição X do carro e a velocidade. Se quisermos que nosso carro dirija no topo da montanha, definimos a recompensa de maneira conveniente: o agente recebe -1 em sua recompensa para cada passo em que não atingiu a meta. Quando atinge a meta, o episódio termina. Então, de fato, o agente é punido por não estar na posição que queremos. Quanto mais rápido ele chegar, melhor para ele. O objetivo do agente é maximizar a recompensa total, que é a soma das recompensas de um episódio. Então, se atingir o ponto desejado após, por exemplo, 110 passos, ele recebe um retorno total de -110, o que seria um ótimo resultado para o Mountain Car, pois se não atingir a meta, ele é punido com 200 passos (portanto, um retorno de -200).

Esta é toda a formulação do problema. Agora, podemos dar isso aos algoritmos, que já são poderosos o suficiente para resolver esses problemas em questão de minutos (se bem ajustados). Vale a pena notar que não dizemos ao agente como atingir o objetivo. Nós nem mesmo fornecemos dicas (heurísticas). O agente encontrará uma maneira (uma política) de vencer por conta própria.

Configurando o Ambiente

Primeiro, copie todo o código do tutorial em seu disco:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Agora, precisamos instalar os pacotes Python que usaremos. Para não instalá-los em seu espaço de usuário (e correr o risco de colisões), vamos limpá-los e instalá-los no ambiente conda. Se você não tiver o conda instalado, siga https://conda.io/docs/user-guide/install/index.html.

Para criar nosso ambiente conda:

 conda create -n tutorial python=3.6.5 -y

Para ativá-lo:

 source activate tutorial

Você deve ver (tutorial) próximo ao seu prompt no shell. Isso significa que um ambiente conda com o nome “tutorial” está ativo. A partir de agora, todos os comandos devem ser executados dentro desse ambiente conda.

Agora, podemos instalar todas as dependências em nosso ambiente conda hermético:

 pip install -r requirements.txt

Terminamos a instalação, então vamos executar algum código. Não precisamos implementar o ambiente Mountain Car por conta própria; a biblioteca OpenAI Gym fornece essa implementação. Vamos ver um agente aleatório (um agente que realiza ações aleatórias) em nosso ambiente:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Este é o arquivo see.py ; para executá-lo, execute:

 python see.py

Você deve ver um carro indo e voltando aleatoriamente. Cada episódio consistirá em 200 passos; o retorno total será de -200.

Agora precisamos substituir ações aleatórias por algo melhor. Existem muitos algoritmos que podem ser usados. Para um tutorial introdutório, acho que uma abordagem chamada deep $Q$-learning é uma boa opção. Compreender esse método fornece uma base sólida para aprender outras abordagens.

Aprendizado profundo de $Q$

O algoritmo que utilizaremos foi descrito pela primeira vez em 2013 por Mnih et al. em Jogando Atari com Aprendizado por Reforço Profundo e aperfeiçoado dois anos depois em Controle de nível humano por meio de aprendizado por reforço profundo. Muitos outros trabalhos são construídos sobre esses resultados, incluindo o atual algoritmo de última geração Rainbow (2017):

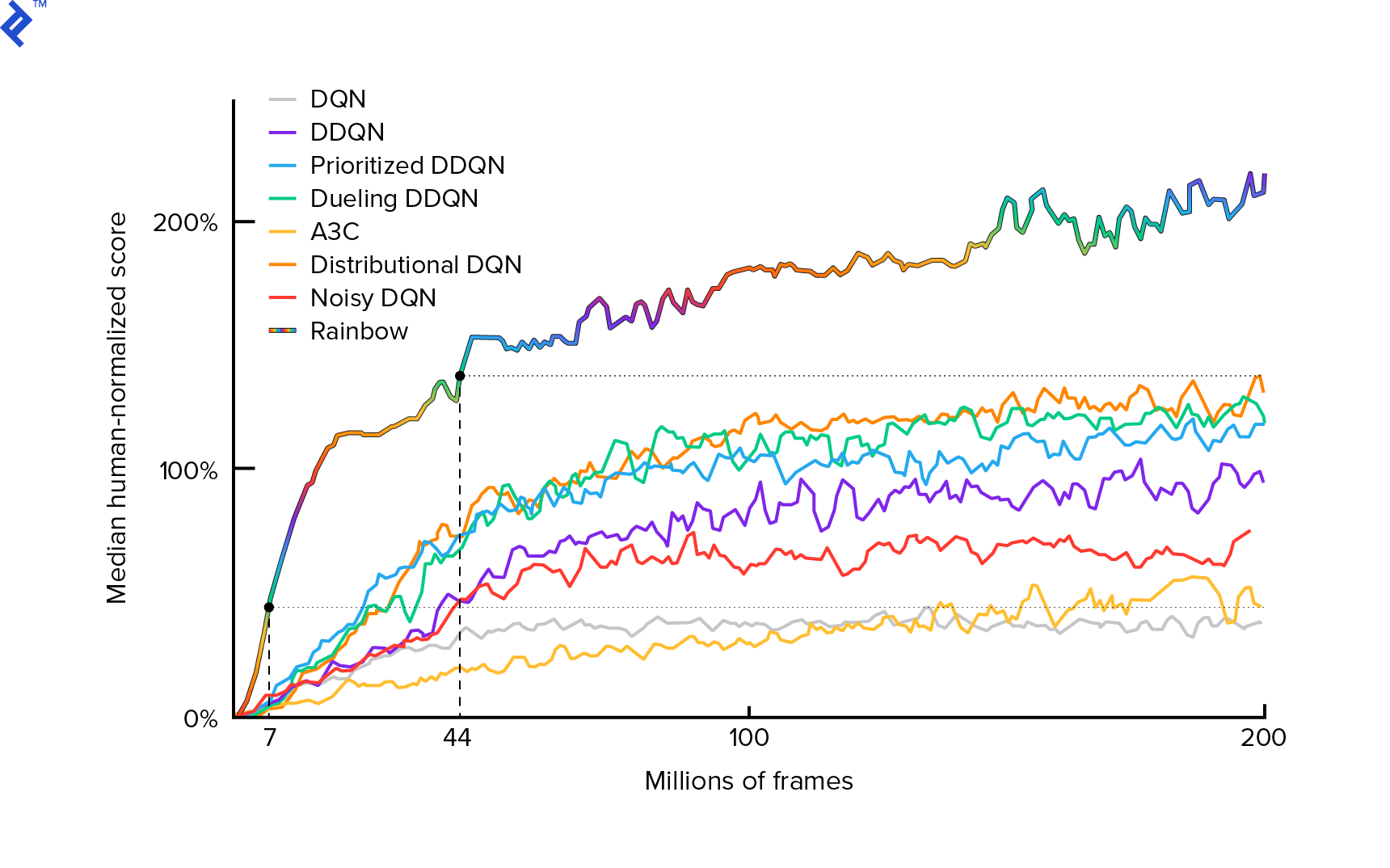
Rainbow alcança desempenho sobre-humano em muitos jogos Atari 2600. Vamos nos concentrar na versão básica do DQN, com o menor número possível de melhorias adicionais, para manter este tutorial em um tamanho razoável.

Uma política, normalmente denotada por $π(s)$, é uma função que retorna probabilidades de realizar ações individuais em um determinado estado $s$. Assim, por exemplo, uma política aleatória da Mountain Car retorna para qualquer estado: 50% à esquerda, 50% à direita. Durante o jogo, tiramos amostras dessa política (distribuição) para obter ações reais.

$Q$-learning (Q é para Qualidade) refere-se à função de valor de ação denotada $Q_π(s, a)$. Retorna o retorno total de um determinado estado $s$, escolhendo a ação $a$, seguindo uma política concreta $π$. O retorno total é a soma de todas as recompensas em um episódio (trajetória).

Se conhecêssemos a função ótima $Q$, denotada $Q^*$, poderíamos resolver o jogo facilmente. Seguiríamos apenas as ações com o maior valor $Q^*$, ou seja, o maior retorno esperado. Isso garante que alcançaremos o maior retorno possível.

No entanto, muitas vezes não sabemos $Q^*$. Nesses casos, podemos aproximar – ou “aprender” – das interações com o ambiente. Esta é a parte “$Q$-learning” no nome. Há também a palavra “deep” nela porque, para aproximar essa função, usaremos redes neurais profundas, que são aproximadores de funções universais. As redes neurais profundas que se aproximam dos valores $Q$ foram denominadas Deep Q-Networks (DQN). Em ambientes simples (com o número de estados cabendo na memória), pode-se usar apenas uma tabela em vez de uma rede neural para representar a função $Q$, caso em que ela seria chamada de “aprendizagem $Q$ tabular”.

Portanto, nosso objetivo agora é aproximar a função $Q^*$. Usaremos a equação de Bellman:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ é o estado após $s$. $γ$ (gama), normalmente 0,99, é um fator de desconto (é um hiperparâmetro). Atribui um peso menor às recompensas futuras (porque elas são menos certas do que as recompensas imediatas com nosso $Q$ imperfeito). A equação de Bellman é fundamental para o aprendizado profundo de $Q$. Ele diz que o valor $Q$ para um determinado estado e ação é uma recompensa $r$ recebida após a ação $a$ mais o valor $Q$ mais alto para o estado em que pousamos em $s'$. O mais alto é no sentido de que estamos escolhendo uma ação $a'$, que leva ao maior retorno total de $s'$.

Com a equação de Bellman, podemos usar o aprendizado supervisionado para aproximar $Q^*$. A função $Q$ será representada (parametrizada) pelos pesos da rede neural denotados como $θ$ (teta). Uma implementação direta levaria um estado e uma ação como a entrada da rede e a saída do valor Q. A ineficiência é que, se quisermos saber os valores de $Q$ para todas as ações em um determinado estado, precisamos chamar $Q$ quantas vezes houver ações. Existe uma maneira muito melhor: pegar apenas o estado como entrada e saída de valores $Q$ para todas as ações possíveis. Graças a isso, podemos obter valores de $Q$ para todas as ações em apenas um passe para frente.

Começamos a treinar a rede $Q$ com pesos aleatórios. Do ambiente, obtemos muitas transições (ou “experiências”). São tuplas de (estado, ação, próximo estado, recompensa) ou, resumindo, ($s$, $a$, $s'$, $r$). Armazenamos milhares deles em um buffer de anel chamado “replay de experiência”. Em seguida, coletamos experiências desse buffer com o desejo de que a equação de Bellman seja válida para elas. Poderíamos ter ignorado o buffer e aplicado as experiências uma a uma (isso é chamado de “online” ou “on-policy”); o problema é que as experiências subsequentes são altamente correlacionadas umas com as outras e o DQN treina mal quando isso ocorre. É por isso que a repetição da experiência foi introduzida (uma abordagem “offline”, “fora da política”) para quebrar essa correlação de dados. O código de nossa implementação mais simples de buffer de anel pode ser encontrado no arquivo replay_buffer.py , encorajo você a lê-lo.

No início, como nossos pesos de rede neural eram aleatórios, o valor do lado esquerdo da equação de Bellman estará longe do lado direito. A diferença ao quadrado será nossa função de perda. Vamos minimizar a função de perda alterando os pesos da rede neural $θ$. Vamos escrever nossa função de perda:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

É uma equação de Bellman reescrita. Digamos que amostramos uma experiência ($s$, esquerda, $s'$, -1) do replay da experiência do Mountain Car. Nós fazemos uma passagem direta pela nossa rede $Q$ com o estado $s$ e para a ação esquerda nos dá -120, por exemplo. Então, $Q(s, \textrm{esquerda}) = -120$. Então nós alimentamos $s'$ para a rede, que nos dá, por exemplo, -130 para a esquerda e -122 para a direita. Então, claramente, a melhor ação para $s'$ está certa, então $\textrm{max}_{a'}Q(s', a') = -122$. Sabemos $r$, esta é a recompensa real, que foi -1. Portanto, nossa previsão de rede $Q$ estava um pouco errada, porque $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Então, propagamos o erro para trás e corrigimos ligeiramente os pesos $θ$. Se calculássemos a perda novamente para a mesma experiência, ela agora seria menor.

Uma observação importante antes de irmos para o código. Vamos notar que, para atualizar nosso DQN, faremos duas passagens para frente no próprio DQN…. Isso muitas vezes leva a um aprendizado instável. Para aliviar isso, para a previsão do próximo estado $Q$, não usamos o mesmo DQN. Usamos uma versão mais antiga dele, que no código é chamada de target_model (ao invés de model , sendo o DQN principal). Graças a isso, temos um alvo estável. Atualizamos target_model definindo-o para pesos de model a cada 1.000 etapas. Mas o model atualiza a cada passo.

Vejamos o código criando o modelo DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Primeiro, a função pega as dimensões do espaço de ação e observação do ambiente OpenAI Gym. É necessário saber, por exemplo, quantas saídas nossa rede terá. Deve ser igual ao número de ações. As ações são uma codificada a quente:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Então (por exemplo) a esquerda será [1, 0] e a direita será [0, 1].

Podemos ver que as observações são passadas como entrada. Também passamos action_mask como uma segunda entrada. Por quê? Ao calcular $Q(s,a)$, precisamos saber o valor de $Q$ apenas para uma determinada ação, não para todas elas. action_mask contém 1 para as ações que queremos passar para a saída DQN. Se action_mask tiver 0 para alguma ação, o valor $Q$ correspondente será zerado na saída. A camada filtered_output está fazendo isso. Se quisermos todos os valores $Q$ (para cálculo máximo), podemos simplesmente passar todos.

O código usa keras.layers.Dense para definir uma camada totalmente conectada. Keras é uma biblioteca Python para abstração de alto nível sobre o TensorFlow. Sob o capô, Keras cria um gráfico TensorFlow, com vieses, inicialização de peso adequada e outras coisas de baixo nível. Poderíamos ter usado o TensorFlow bruto para definir o gráfico, mas não será uma linha única.

Assim, as observações são passadas para a primeira camada oculta, com ativações de ReLU (unidade linear retificada). ReLU(x) é apenas uma função $\textrm{max}(0, x)$. Essa camada está totalmente conectada com uma segunda idêntica, hidden_2 . A camada de saída reduz o número de neurônios para o número de ações. No final, temos filtered_output , que apenas multiplica a saída por action_mask .

Para encontrar pesos $θ$, usaremos um otimizador chamado “Adam” com uma perda de erro quadrático médio.

Tendo um modelo, podemos usá-lo para prever valores $Q$ para determinadas observações de estado:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Queremos valores $Q$ para todas as ações, portanto action_mask é um vetor de uns.

Para fazer o treinamento real, usaremos fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

O Lote contém experiências BATCH_SIZE . next_q_values ​​é $Q(s, a)$. q_values ​​é $r + γ \space \textrm{max}_{a'}Q(s', a')$ da equação de Bellman. As ações que tomamos são codificadas a quente e passadas como action_mask para a entrada ao chamar model.fit() . $y$ é uma letra comum para um “alvo” na aprendizagem supervisionada. Aqui estamos passando os q_values ​​. Eu faço q_values[:. None] q_values[:. None] para aumentar a dimensão do array porque deve corresponder à dimensão do array one_hot_actions . Isso é chamado de notação de fatia se você quiser ler mais sobre isso.

Retornamos a perda para salvá-la no arquivo de log do TensorBoard e depois visualizar. Há muitas outras coisas que vamos monitorar: quantos passos por segundo fazemos, uso total de RAM, qual é o retorno médio de episódios, etc. Vamos ver esses gráficos.

Correndo

Para visualizar o arquivo de log do TensorBoard, primeiro precisamos ter um. Então, vamos apenas executar o treinamento:

 python run.py

Isso imprimirá primeiro o resumo do nosso modelo. Em seguida, ele criará um diretório de log com a data atual e iniciará o treinamento. A cada 2000 passos, uma logline será impressa semelhante a esta:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

A cada 20.000, avaliaremos nosso modelo em 10.000 etapas:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Após 677 episódios e 120.000 passos, o retorno médio dos episódios melhorou de -200 para -136,75! Com certeza é aprendizado. O que é avg_max_q_value estou deixando como um bom exercício para o leitor. Mas é uma estatística muito útil de se observar durante o treinamento.

Após 200.000 passos, nosso treinamento está concluído. Na minha CPU de quatro núcleos, leva cerca de 20 minutos. Podemos olhar dentro do diretório date-log , por exemplo, 06-07-18-39-log . Haverá quatro arquivos de modelo com a extensão .h5 . Este é um instantâneo dos pesos do gráfico do TensorFlow, nós os salvamos a cada 50.000 etapas para depois dar uma olhada na política que aprendemos. Para visualizá-lo:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Para ver os outros sinalizadores possíveis: python run.py --help .

Agora, o carro está fazendo um trabalho muito melhor para atingir o objetivo desejado. No diretório date-log , há também o arquivo events.out.* . Este é o arquivo onde o TensorBoard armazena seus dados. Nós escrevemos nele usando o TensorBoardLogger mais simples definido em loggers.py. Para visualizar o arquivo de eventos, precisamos executar o servidor TensorBoard local:

 tensorboard --logdir=.

--logdir apenas aponta para o diretório em que existem diretórios de log de datas, no nosso caso, este será o diretório atual, portanto . . O TensorBoard imprime a URL na qual está escutando. Se você abrir http://127.0.0.1:6006, deverá ver oito gráficos semelhantes a estes:

Empacotando

train() faz todo o treinamento. Primeiro criamos o modelo e reproduzimos o buffer. Então, em um loop muito semelhante ao de see.py , interagimos com o ambiente e armazenamos experiências no buffer. O importante é seguirmos uma política gananciosa de épsilon. Podemos sempre escolher a melhor ação de acordo com a função $Q$; no entanto, isso desencoraja a exploração, o que prejudica o desempenho geral. Então, para reforçar a exploração com probabilidade épsilon, realizamos ações aleatórias:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon foi ajustado para 1%. Após 2000 experiências, o replay enche o suficiente para iniciar o treinamento. Fazemos isso chamando fit_batch() com um lote aleatório de experiências amostradas do buffer de repetição:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

A cada 20.000 passos, avaliamos e registramos os resultados (a avaliação é com epsilon = 0 , política totalmente gananciosa):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

O código inteiro tem cerca de 300 linhas e run.py contém cerca de 250 das mais importantes.

Pode-se notar que existem muitos hiperparâmetros:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

E isso nem são todos eles. Há também uma arquitetura de rede - usamos duas camadas ocultas com 32 neurônios, ativações ReLU e otimizador Adam, mas há muitas outras opções. Mesmo pequenas mudanças podem ter um enorme impacto no treinamento. Muito tempo pode ser gasto ajustando hiperparâmetros. Em uma recente competição OpenAI, um competidor em segundo lugar descobriu que é possível quase dobrar a pontuação do Rainbow após o ajuste de hiperparâmetros. Naturalmente, é preciso lembrar que é fácil overfit. Atualmente, os algoritmos de reforço estão lutando com a transferência de conhecimento para ambientes semelhantes. Nosso Mountain Car não generaliza para todos os tipos de montanhas no momento. Você pode realmente modificar o ambiente OpenAI Gym e ver até que ponto o agente pode generalizar.

Outro exercício será encontrar um conjunto de hiperparâmetros melhor do que o meu. É definitivamente possível. No entanto, uma corrida de treinamento não será suficiente para julgar se sua mudança é uma melhoria. Geralmente há uma grande diferença entre as corridas de treinamento; a variação é grande. Você precisaria de muitas corridas para determinar que algo é melhor. Se você quiser ler mais sobre um tópico tão importante como reprodutibilidade, eu o encorajo a ler Deep Reinforcement Learning that Matters. Em vez de ajustar manualmente, podemos automatizar esse processo até certo ponto - se estivermos dispostos a gastar mais poder de computação no problema. Uma abordagem simples é preparar uma faixa promissora de valores para alguns hiperparâmetros e então executar uma busca em grade (verificando suas combinações), com treinamentos sendo executados em paralelo. A paralelização em si é um grande tópico por si só, pois é crucial para o alto desempenho.

Deep $Q$-learning representa uma grande família de algoritmos de aprendizado por reforço que usam iteração de valor. Tentamos aproximar a função $Q$, e a usamos de maneira gananciosa na maioria das vezes. Há outra família que usa a iteração de política. Eles não se concentram em aproximar a função $Q$, mas em encontrar a política ótima $π^*$ diretamente. Para ver onde a iteração de valor se encaixa no cenário dos algoritmos de aprendizado por reforço:

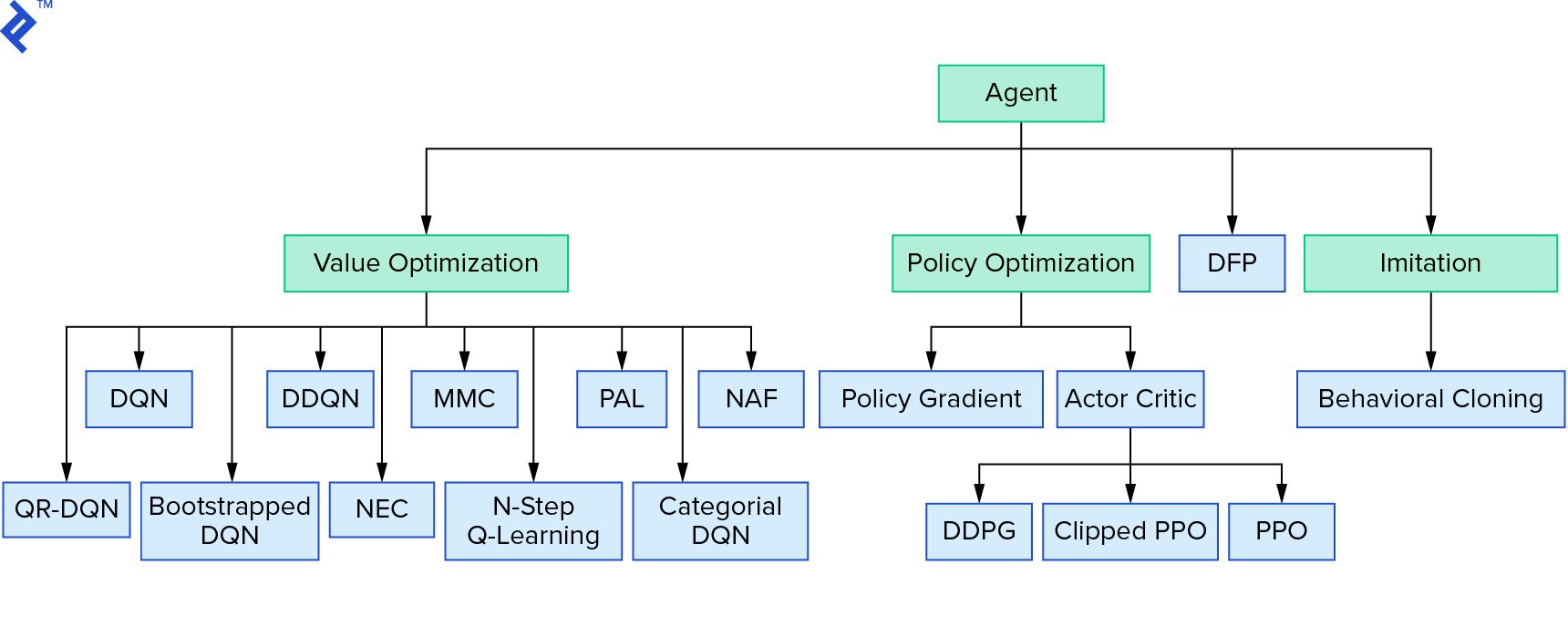
Seus pensamentos podem ser que o aprendizado por reforço profundo parece frágil. Você estará certo; há muitos problemas. Você pode consultar Deep Reinforcement Learning ainda não funciona e Reinforcement Learning nunca funcionou, e 'profundo' só ajudou um pouco.

Isso encerra o tutorial. Implementamos nosso próprio DQN básico para fins de aprendizado. Código muito semelhante pode ser usado para obter um bom desempenho em alguns jogos do Atari. Em aplicações práticas, muitas vezes são feitas implementações testadas e de alto desempenho, por exemplo, uma das linhas de base do OpenAI. Se você quiser ver quais desafios podem ser enfrentados ao tentar aplicar o aprendizado por reforço profundo em um ambiente mais complexo, leia Nossa abordagem NIPS 2017: Learning to Run. Se você quiser aprender mais em um ambiente de competição divertido, dê uma olhada em NIPS 2018 Competitions ou crowdai.org.

Se você está prestes a se tornar um especialista em aprendizado de máquina e gostaria de aprofundar seu conhecimento em aprendizado supervisionado, confira Análise de vídeo de aprendizado de máquina: Identificando peixes para um experimento divertido sobre identificação de peixes.