深入了解強化學習

讓我們深入了解強化學習。 在本文中，我們將解決 TensorFlow、TensorBoard、Keras 和 OpenAI gym 等現代庫的具體問題。 您將看到如何實現一種稱為深度 $Q$-learning 的基本算法來了解其內部工作原理。 關於硬件，整個代碼將在典型的 PC 上運行並使用所有找到的 CPU 內核（這由 TensorFlow 開箱即用地處理）。

這個問題被稱為山車：一輛汽車在一維軌道上，位於兩座山之間。 目標是在右邊開車上山（到達國旗）。 但是，這輛車的發動機不夠強大，無法單程爬山。 因此，成功的唯一方法是來回驅動以積蓄動力。

選擇這個問題是因為它很簡單，可以在幾分鐘內在單個 CPU 內核上找到強化學習的解決方案。 但是，它足夠複雜，無法成為一個好的代表。

首先，我將簡要總結一下強化學習的一般作用。 然後，我們將介紹基本術語並表達我們對它們的問題。 之後，我將描述深度 $Q$ 學習算法，我們將實施它來解決問題。

強化學習基礎

用最簡單的話來說，強化學習就是通過反複試驗來學習。 主角被稱為“代理人”，這將是我們問題中的汽車。 智能體在環境中做出動作，並獲得新的觀察結果和對該動作的獎勵。 導致更大回報的行動得到加強，因此得名。 與計算機科學中的許多其他事情一樣，這一點也受到觀察生物的啟發。

下圖總結了代理與環境的交互：

代理會因執行的操作而獲得觀察和獎勵。 然後它進行另一個動作並執行第二步。 環境現在返回（可能）略有不同的觀察和獎勵。 這一直持續到達到終端狀態，通過向代理髮送“完成”來發出信號。 觀察 > 動作 > next_observations > 獎勵的整個序列稱為情節（或軌跡）。

回到我們的山地車：我們的車是代理。 環境是一維山脈的黑箱世界。 汽車的動作歸結為只有一個數字：如果是正數，則發動機將汽車推向右側。 如果為負，則將汽車向左推。 代理通過觀察來感知環境：汽車的 X 位置和速度。 如果我們希望我們的汽車在山頂上行駛，我們以一種方便的方式定義獎勵：代理在它沒有達到目標的每一步中獲得 -1 的獎勵。 當它達到目標時，這一集就結束了。 所以，事實上，代理人因為沒有處於我們想要的位置而受到懲罰。 他越快到達它，對他就越好。 代理的目標是最大化總獎勵，這是一個情節的獎勵總和。 因此，如果它在例如 110 步之後到達期望的點，它會收到 -110 的總回報，這對 Mountain Car 來說將是一個很好的結果，因為如果它沒有達到目標，那麼它會被懲罰 200 步（因此，返回 -200）。

這是整個問題的表述。 現在，我們可以把它交給算法，這些算法已經足夠強大，可以在幾分鐘內解決這些問題（如果調整得當的話）。 值得注意的是，我們並沒有告訴代理如何實現目標。 我們甚至不提供任何提示（啟發式）。 代理人將找到一種方式（政策）以自己獲勝。

設置環境

首先，將整個教程代碼複製到您的磁盤上：

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

現在，我們需要安裝我們將使用的 Python 包。 為了不將它們安裝在您的用戶空間中（並有衝突的風險），我們將使其乾淨並將它們安裝在 conda 環境中。 如果您沒有安裝 conda，請按照 https://conda.io/docs/user-guide/install/index.html 操作。

創建我們的 conda 環境：

 conda create -n tutorial python=3.6.5 -y

要激活它：

 source activate tutorial

您應該在 shell 的提示符附近看到(tutorial) 。 這意味著名為“tutorial”的 conda 環境處於活動狀態。 從現在開始，所有命令都應該在該 conda 環境中執行。

現在，我們可以在密封 conda 環境中安裝所有依賴項：

 pip install -r requirements.txt

我們已經完成了安裝，所以讓我們運行一些代碼。 我們不需要自己實現 Mountain Car 環境； OpenAI Gym 庫提供了該實現。 讓我們看看我們環境中的一個隨機代理（一個採取隨機動作的代理）：

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

這是see.py文件； 要運行它，請執行：

 python see.py

你應該看到一輛汽車隨機來回行駛。 每集將包含 200 個步驟； 總回報將是-200。

現在我們需要用更好的東西替換隨機動作。 有很多算法可以使用。 對於介紹性教程，我認為一種稱為深度 $Q$-learning 的方法非常適合。 理解該方法為學習其他方法奠定了堅實的基礎。

深度$Q$-學習

我們將使用的算法於 2013 年由 Mnih 等人首次描述。 在用深度強化學習玩 Atari 並在兩年後通過深度強化學習在人類水平控制方面進行了打磨。 許多其他工作都建立在這些結果之上，包括當前最先進的算法 Rainbow（2017）：

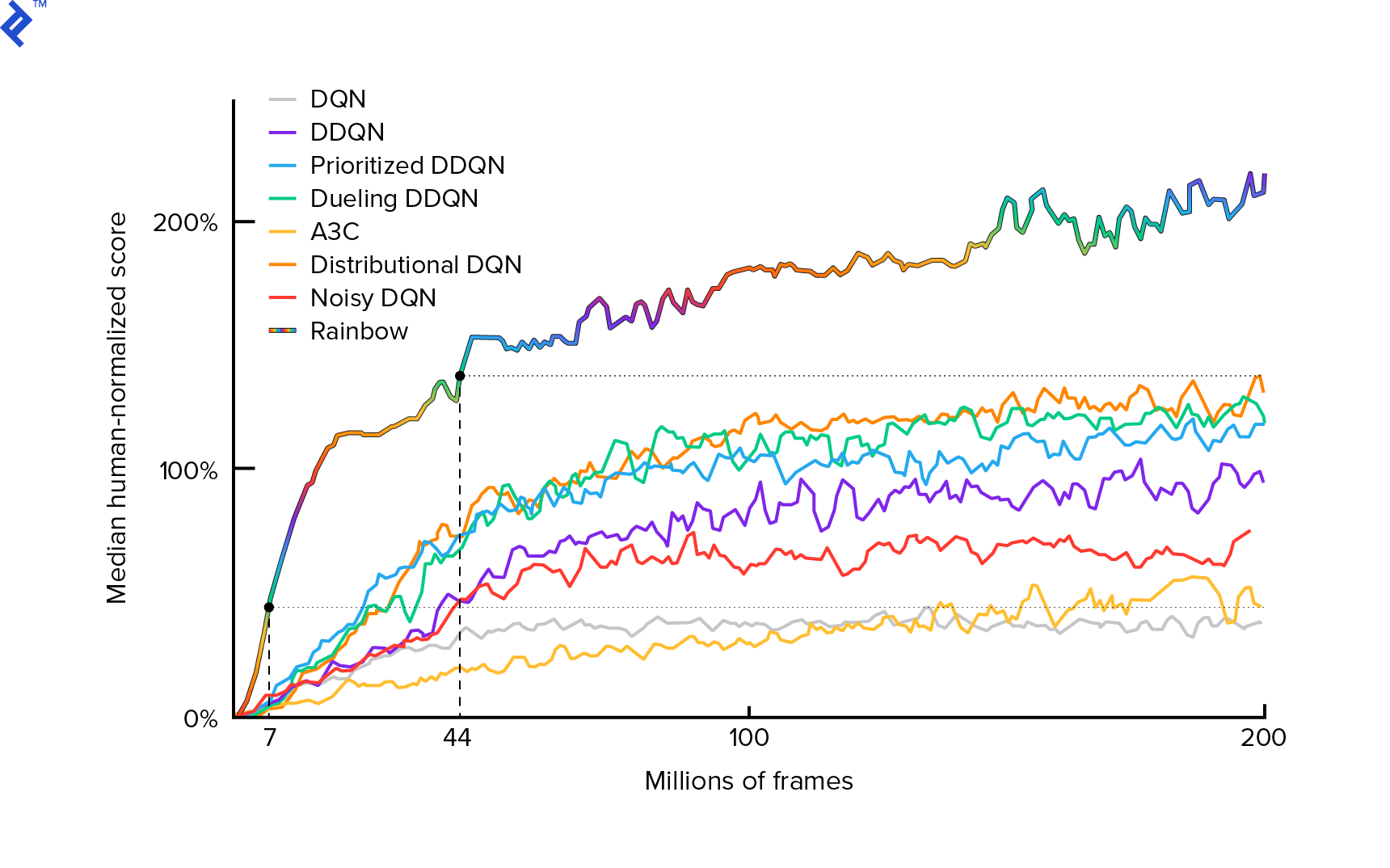
Rainbow 在許多 Atari 2600 遊戲中實現了超人的性能。 我們將專注於基本的 DQN 版本，並儘可能少地進行一些額外的改進，以使本教程保持合理的大小。

策略，通常表示為 $π(s)$，是一個函數，它返回在給定狀態 $s$ 中採取個人行動的概率。 因此，例如，對於任何狀態，隨機 Mountain Car 策略都會返回：50% 左，50% 右。 在遊戲過程中，我們從該策略（分佈）中採樣以獲得實際動作。

$Q$-learning（Q 代表質量）指的是表示為 $Q_π(s,a)$ 的動作價值函數。 它返回給定狀態 $s$ 的總回報，選擇動作 $a$，遵循具體策略 $π$。 總回報是一集（軌跡）中所有獎勵的總和。

如果我們知道最優的$Q$-函數，記為$Q^*$，我們可以很容易地解決這個遊戲。 我們將只遵循具有最高價值 $Q^*$ 的行動，即最高預期回報。 這保證了我們將獲得盡可能高的回報。

然而，我們常常不知道$Q^*$。 在這種情況下，我們可以從與環境的交互中近似或“學習”它。 這是名稱中的“$Q$-learning”部分。 其中還有“深度”一詞，因為為了逼近該函數，我們將使用深度神經網絡，它是通用函數逼近器。 近似 $Q$-values 的深度神經網絡被命名為 Deep Q-Networks (DQN)。 在簡單的環境中（狀態數適合內存），可以只使用表格而不是神經網絡來表示 $Q$-function，在這種情況下，它將被命名為“表格 $Q$-learning”。

所以我們現在的目標是逼近 $Q^*$ 函數。 我們將使用貝爾曼方程：

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ 是 $s$ 之後的狀態。 $γ$ (gamma)，通常為 0.99，是一個折扣因子（它是一個超參數）。 它對未來獎勵的權重較小（因為它們比我們不完美的 $Q$ 的即時獎勵更不確定）。 貝爾曼方程是深度 $Q$ 學習的核心。 它表示給定狀態和動作的 $Q$-value 是在採取行動 $a$ 後收到的獎勵 $r$加上我們在 $s'$ 所在狀態的最高 $Q$-value。 從某種意義上說，最高的是我們正在選擇一個動作$a'$，這導致$s'$的總回報最高。

通過貝爾曼方程，我們可以使用監督學習來逼近 $Q^*$。 $Q$ 函數將由表示為 $θ$ (theta) 的神經網絡權重表示（參數化）。 一個簡單的實現會將一個狀態和一個動作作為網絡輸入並輸出 Q 值。 效率低下的是，如果我們想知道給定狀態下所有動作的 $Q$-values，我們需要調用 $Q$ 的次數與動作的次數一樣多。 有一個更好的方法：只將狀態作為輸入並為所有可能的操作輸出 $Q$-values。 多虧了這一點，我們可以在一次前向傳遞中獲得所有動作的 $Q$-values。

我們開始用隨機權重訓練 $Q$ 網絡。 從環境中，我們獲得了許多轉變（或“經驗”）。 這些是 (state, action, next state, reward) 的元組，或者簡而言之，是 ($s$, $a$, $s'$, $r$)。 我們將數千個它們存儲在一個稱為“體驗重放”的環形緩衝區中。 然後，我們從該緩衝區中採樣經驗，希望貝爾曼方程適用於他們。 我們可以跳過緩衝區並一個一個地應用經驗（這被稱為“在線”或“on-policy”）； 問題是隨後的經驗彼此高度相關，並且當這種情況發生時，DQN 訓練很差。 這就是為什麼引入體驗回放（一種“離線”、“離線”方法）來打破這種數據相關性。 我們最簡單的環形緩衝區實現的代碼可以在replay_buffer.py文件中找到，我鼓勵你閱讀它。

一開始，由於我們的神經網絡權重是隨機的，貝爾曼方程的左側值將遠離右側。 平方差將是我們的損失函數。 我們將通過改變神經網絡權重 $θ$ 來最小化損失函數。 讓我們寫下我們的損失函數：

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

這是一個重寫的貝爾曼方程。 假設我們從 Mountain Car 體驗回放中採樣了一次體驗（$s$, left, $s'$, -1）。 例如，我們通過狀態為 $s$ 的 $Q$ 網絡進行前向傳遞，對於左側的動作，它給我們 -120。 所以，$Q(s, \textrm{left}) = -120$。 然後我們將 $s'$ 輸入到網絡中，這給了我們，例如，左側為 -130，右側為 -122。 很明顯，$s'$ 的最佳操作是正確的，因此 $\textrm{max}_{a'}Q(s', a') = -122$。 我們知道$r$，這是真正的獎勵，是-1。 所以我們的 $Q$-network 預測有點錯誤，因為 $L(θ) = [-120 - 1 + 0.99 ⋅ 122]^2 = (-0.22^2) = 0.0484$。 所以我們向後傳播誤差並稍微修正權重$θ$。 如果我們要再次計算相同體驗的損失，現在它會更低。

在我們開始編碼之前的一個重要觀察。 讓我們注意，為了更新我們的 DQN，我們將對 DQN 本身進行兩次前向傳遞。 這通常會導致學習不穩定。 為了緩解這種情況，對於下一個狀態 $Q$ 預測，我們不使用相同的 DQN。 我們使用它的舊版本，在代碼中稱為target_model （而不是model ，是主要的 DQN）。 多虧了這一點，我們有了一個穩定的目標。 我們通過將target_model設置為每 1000 步的model權重來更新它。 但是model每一步都會更新。

讓我們看一下創建 DQN 模型的代碼：

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

首先，該函數從給定的 OpenAI Gym 環境中獲取動作和觀察空間的維度。 例如，有必要知道我們的網絡將有多少輸出。 它必須等於動作的數量。 動作是一種熱編碼：

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

所以（例如）左邊是[1, 0]，右邊是[0, 1]。

我們可以看到觀察結果作為輸入傳遞。 我們還將action_mask作為第二個輸入傳遞。 為什麼？ 在計算 $Q(s,a)$ 時，我們只需要知道一個給定動作的 $Q$-value，而不是所有動作。 action_mask包含 1 表示我們要傳遞給 DQN 輸出的操作。 如果action_mask的某個動作為 0，則相應的 $Q$-value 將在輸出上歸零。 filtered_output層就是這樣做的。 如果我們想要所有的 $Q$ 值（用於最大值計算），我們可以傳遞所有的值。

代碼使用keras.layers.Dense定義全連接層。 Keras 是一個 Python 庫，用於在 TensorFlow 之上進行更高級別的抽象。 在底層，Keras 創建了一個 TensorFlow 圖，其中包含偏差、適當的權重初始化和其他低級別的東西。 我們本可以只使用原始 TensorFlow 來定義圖形，但它不會是單行的。

所以觀察被傳遞到第一個隱藏層，帶有 ReLU（校正線性單元）激活。 ReLU(x)只是一個 $\textrm{max}(0, x)$ 函數。 該層與第二個相同的層hidden_2 ​​2 完全連接。 輸出層將神經元的數量減少到動作的數量。 最後，我們得到了filtered_output ，它只是將輸出與action_mask 。

為了找到 $θ$ 權重，我們將使用一個名為“Adam”的優化器，它具有均方誤差損失。

有了一個模型，我們可以用它來預測給定狀態觀察的 $Q$ 值：

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

我們想要所有動作的 $Q$-values，因此action_mask是一個向量。

為了進行實際訓練，我們將使用fit_batch() ：

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Batch 包含BATCH_SIZE體驗。 next_q_values是 $Q(s, a)$。 q_values是來自貝爾曼方程的 $r + γ \space \textrm{max}_{a'}Q(s', a')$。 我們採取的行動是一種熱編碼，並在調用model.fit()時作為action_mask傳遞給輸入。 $y$ 是監督學習中“目標”的常用字母。 這裡我們傳遞q_values 。 我做q_values[:. None] q_values[:. None]增加數組維度，因為它必須對應於one_hot_actions數組的維度。 如果您想了解更多有關它的信息，這稱為切片表示法。

我們返回損失以將其保存在 TensorBoard 日誌文件中，然後進行可視化。 我們將監控許多其他事情：我們每秒執行多少步、總 RAM 使用量、平均劇集回報是多少等。讓我們看看這些圖。

跑步

為了可視化 TensorBoard 日誌文件，我們首先需要一個。 所以讓我們開始訓練：

 python run.py

這將首先打印我們模型的摘要。 然後它將創建一個包含當前日期的日誌目錄並開始訓練。 每 2000 步，將打印一條日誌行，如下所示：

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

每 20,000 次，我們將在 10,000 步上評估我們的模型：

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

在 677 集和 120,000 步之後，平均集回報從 -200 提高到 -136.75！ 絕對是在學習。 什麼avg_max_q_value是我留給讀者的一個很好的練習。 但這是在訓練期間查看的非常有用的統計數據。

200,000 步之後，我們的訓練就完成了。 在我的四核 CPU 上，大約需要 20 分鐘。 我們可以查看date-log目錄，例如06-07-18-39-log 。 將有四個擴展名為.h5的模型文件。 這是 TensorFlow 圖權重的快照，我們每 50,000 步保存一次，以便稍後查看我們學到的策略。 要查看它：

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

要查看其他可能的標誌： python run.py --help 。

現在，汽車在達到預期目標方面做得更好。 在date-log目錄中，還有events.out.*文件。 這是 TensorBoard 存儲其數據的文件。 我們使用TensorBoardLogger中定義的最簡單的 TensorBoardLogger 對其進行loggers.py. 要查看事件文件，我們需要運行本地 TensorBoard 服務器：

 tensorboard --logdir=.

--logdir只是指向包含日期日誌目錄的目錄，在我們的例子中，這將是當前目錄，所以. . TensorBoard 打印它正在偵聽的 URL。 如果你打開 http://127.0.0.1:6006，你應該會看到八個類似的圖：

包起來

train()完成所有訓練。 我們首先創建模型並重放緩衝區。 然後，在與see.py中的循環非常相似的循環中，我們與環境交互並將體驗存儲在緩衝區中。 重要的是我們遵循 epsilon-greedy 策略。 我們總是可以根據 $Q$-function 選擇最佳動作； 但是，這會阻礙探索，從而損害整體性能。 因此，為了使用 epsilon 概率進行探索，我們執行隨機操作：

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon 設置為 1%。 在 2000 次體驗之後，回放充滿足以開始訓練。 我們通過調用fit_batch()來實現，其中包含從重放緩衝區中採樣的隨機一批經驗：

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

每 20,000 步，我們評估並記錄結果（評估是使用epsilon = 0 ，完全貪婪的策略）：

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

整個代碼大約 300 行， run.py包含大約 250 個最重要的代碼。

可以注意到有很多超參數：

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

這甚至不是全部。 還有一個網絡架構——我們使用了兩個具有 32 個神經元的隱藏層、ReLU 激活和 Adam 優化器，但還有很多其他選項。 即使是很小的變化也會對培訓產生巨大影響。 可以花費大量時間調整超參數。 在最近的 OpenAI 比賽中，一位獲得第二名的選手發現，在超參數調優後，Rainbow 的分數幾乎可以翻倍。 自然，人們必須記住，過擬合很容易。 目前，強化算法正在努力將知識轉移到類似環境。 我們的 Mountain Car 目前還不能推廣到所有類型的山脈。 你實際上可以修改 OpenAI Gym 環境，看看代理可以泛化到什麼程度。

另一個練習是找到一組比我更好的超參數。 這絕對是可能的。 然而，一次訓練並不足以判斷你的改變是否是一種進步。 訓練運行之間通常存在很大差異； 方差很大。 您需要多次運行才能確定某些東西更好。 如果您想了解更多關於可重複性等重要主題的信息，我鼓勵您閱讀重要的深度強化學習。 如果我們願意在這個問題上花費更多的計算能力，我們可以在一定程度上自動化這個過程，而不是手動調整。 一種簡單的方法是為一些超參數準備一個有希望的值範圍，然後運行網格搜索（檢查它們的組合），並行運行訓練。 並行化本身就是一個很大的話題，因為它對高性能至關重要。

深度 $Q$-learning 代表了一大類使用值迭代的強化學習算法。 我們試圖逼近 $Q$ 函數，但大多數時候我們只是以貪婪的方式使用它。 還有另一個家庭使用策略迭代。 他們不專注於逼近$Q$-函數，而是直接找到最優策略$π^*$。 要查看值迭代在強化學習算法領域中的位置：

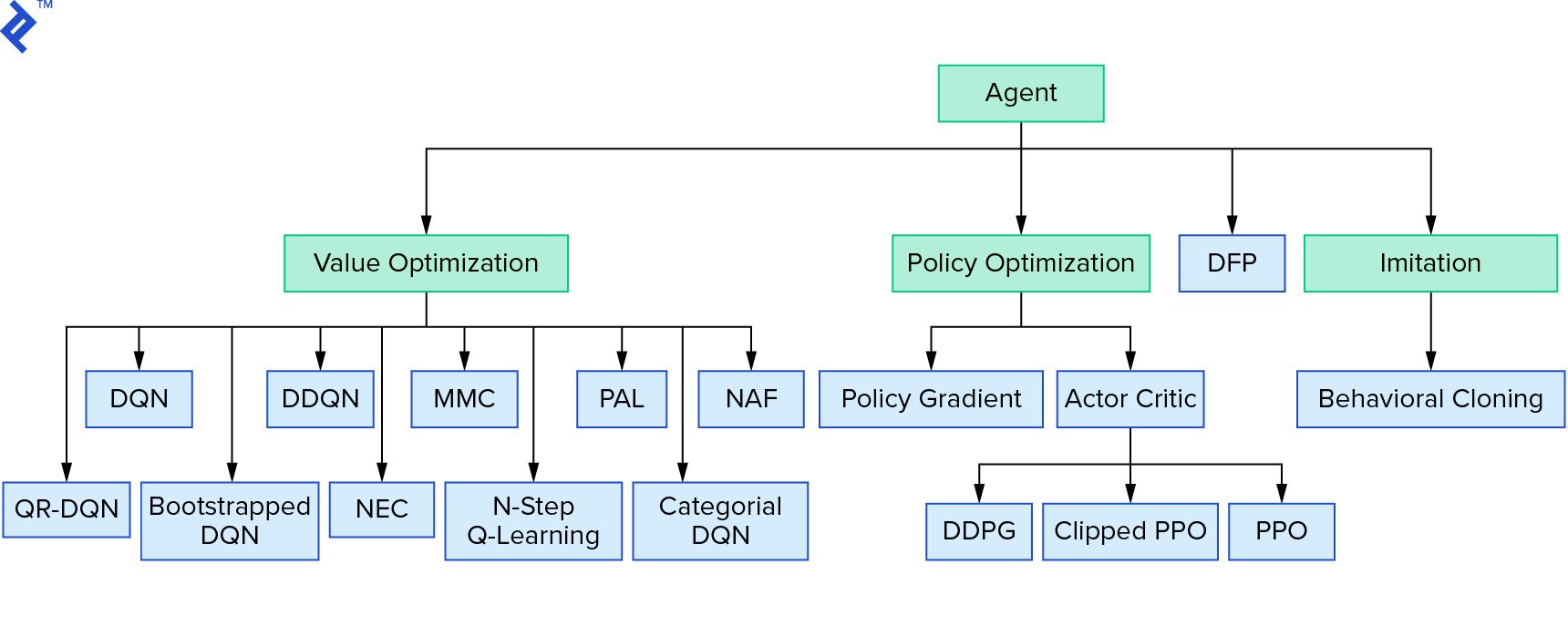
你的想法可能是深度強化學習看起來很脆弱。 你是對的； 有很多問題。 你可以參考 Deep Reinforcement Learning doesn't Work Yet 和 Reinforcement Learning never work ，而“deep”只是有點幫助。

教程到此結束。 為了學習目的，我們實現了自己的基本 DQN。 非常相似的代碼可用於在某些 Atari 遊戲中實現良好的性能。 在實際應用中，通常需要經過測試的高性能實現，例如來自 OpenAI 基線的一種。 如果您想了解在更複雜的環境中嘗試應用深度強化學習時會面臨哪些挑戰，您可以閱讀 Our NIPS 2017：Learning to Run 方法。 如果您想在有趣的比賽環境中了解更多信息，請查看 NIPS 2018 Competitions 或 crowdai.org。

如果您正在成為機器學習專家並希望加深您在監督學習方面的知識，請查看機器學習視頻分析：識別魚，了解有關識別魚的有趣實驗。