Głębokie zanurzenie w uczeniu się przez wzmacnianie

Przyjrzyjmy się głębokiemu uczeniu się przez wzmacnianie. W tym artykule zajmiemy się konkretnym problemem z nowoczesnymi bibliotekami, takimi jak TensorFlow, TensorBoard, Keras i siłownia OpenAI. Zobaczysz, jak zaimplementować jeden z podstawowych algorytmów, zwany głęboką nauką $Q$, aby poznać jego wewnętrzne działanie. Jeśli chodzi o sprzęt, cały kod będzie działał na typowym komputerze i będzie wykorzystywał wszystkie znalezione rdzenie procesora (jest to obsługiwane od razu przez TensorFlow).

Problem nazywa się Mountain Car: samochód jest na jednowymiarowym torze, umieszczonym między dwiema górami. Celem jest wjechanie na górę po prawej (dotarcie do flagi). Jednak silnik samochodu nie jest wystarczająco mocny, aby jednym przejazdem wspiąć się na górę. Dlatego jedynym sposobem na sukces jest jazda tam iz powrotem, aby nabrać rozpędu.

Ten problem został wybrany, ponieważ jest wystarczająco proste, aby znaleźć rozwiązanie z uczeniem wzmocnienia w ciągu kilku minut na jednym rdzeniu procesora. Jest jednak wystarczająco złożony, by być dobrym reprezentantem.

Najpierw przedstawię krótkie podsumowanie tego, co ogólnie robi uczenie się ze wzmocnieniem. Następnie omówimy podstawowe pojęcia i za ich pomocą przedstawimy nasz problem. Następnie opiszę algorytm głębokiego uczenia $Q$ i zaimplementujemy go, aby rozwiązać problem.

Podstawy uczenia się przez wzmacnianie

Nauka ze wzmacnianiem w najprostszych słowach to nauka metodą prób i błędów. Główny bohater nazywany jest „agentem”, który byłby samochodem w naszym problemie. Agent wykonuje akcję w środowisku i otrzymuje z powrotem nową obserwację i nagrodę za to działanie. Działania prowadzące do większych nagród są wzmocnione, stąd nazwa. Podobnie jak w przypadku wielu innych rzeczy w informatyce, również ten został zainspirowany obserwowaniem żywych stworzeń.

Interakcje agenta ze środowiskiem podsumowano na poniższym wykresie:

Agent otrzymuje obserwację i nagrodę za wykonaną akcję. Następnie wykonuje kolejną akcję i wykonuje krok drugi. Środowisko zwraca teraz (prawdopodobnie) nieco inną obserwację i nagrodę. Trwa to aż do osiągnięcia stanu terminala, sygnalizowanego wysłaniem „gotowe” do agenta. Cała sekwencja obserwacji > działania > następna_obserwacja > nagrody nazywana jest epizodem (lub trajektorią).

Wracając do naszego Mountain Car: nasz samochód jest agentem. Środowisko to czarnoskrzynkowy świat jednowymiarowych gór. Akcja samochodu sprowadza się tylko do jednej liczby: jeśli jest dodatnia, silnik popycha samochód w prawo. Jeśli jest ujemny, popycha samochód w lewo. Agent postrzega otoczenie poprzez obserwację: położenie i prędkość samochodu w osi X. Jeśli chcemy, aby nasz samochód wjechał na szczyt góry, nagrodę definiujemy w wygodny sposób: Agent dostaje -1 do swojej nagrody za każdy krok, w którym nie osiągnął celu. Gdy osiągnie cel, odcinek się kończy. Tak więc w rzeczywistości agent jest karany za to, że nie znajduje się w pozycji, w jakiej chcielibyśmy, aby była. Im szybciej do niego dotrze, tym lepiej dla niego. Celem agenta jest maksymalizacja całkowitej nagrody, która jest sumą nagród z jednego odcinka. Czyli jeśli osiągnie upragniony punkt po np. 110 krokach, to otrzyma łączny zwrot -110, co byłoby świetnym wynikiem dla Mountain Car, bo jeśli nie dojedzie do celu, to jest karane na 200 kroków (stąd zwrot -200).

To jest całe sformułowanie problemu. Teraz możemy dać to algorytmom, które są już wystarczająco potężne, aby rozwiązać takie problemy w ciągu kilku minut (jeśli są dobrze dostrojone). Warto zauważyć, że nie mówimy agentowi, jak osiągnąć cel. Nie podajemy nawet żadnych podpowiedzi (heurystyk). Agent sam znajdzie sposób (politykę) na wygraną.

Konfigurowanie środowiska

Najpierw skopiuj cały kod samouczka na dysk:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Teraz musimy zainstalować pakiety Pythona, których będziemy używać. Aby nie instalować ich w Twojej przestrzeni użytkownika (i ryzykować kolizji), wyczyścimy je i zainstalujemy w środowisku conda. Jeśli nie masz zainstalowanego conda, postępuj zgodnie z https://conda.io/docs/user-guide/install/index.html.

Aby stworzyć nasze środowisko conda:

 conda create -n tutorial python=3.6.5 -y

Aby go aktywować:

 source activate tutorial

Powinieneś zobaczyć (tutorial) obok znaku zachęty w powłoce. Oznacza to, że aktywne jest środowisko conda o nazwie „tutorial”. Od tej chwili wszystkie polecenia powinny być wykonywane w tym środowisku conda.

Teraz możemy zainstalować wszystkie zależności w naszym hermetycznym środowisku conda:

 pip install -r requirements.txt

Skończyliśmy z instalacją, więc uruchommy trochę kodu. Nie musimy sami wdrażać środowiska Mountain Car; biblioteka OpenAI Gym zapewnia taką implementację. Zobaczmy losowego agenta (agenta, który wykonuje losowe akcje) w naszym środowisku:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

To jest plik see.py ; aby go uruchomić, wykonaj:

 python see.py

Powinieneś zobaczyć samochód jadący losowo tam iz powrotem. Każdy odcinek będzie składał się z 200 kroków; całkowity zwrot wyniesie -200.

Teraz musimy zastąpić losowe działania czymś lepszym. Istnieje wiele algorytmów, których można użyć. Jeśli chodzi o samouczek wprowadzający, myślę, że podejście zwane głębokim uczeniem się $Q$ jest dobrym rozwiązaniem. Zrozumienie tej metody daje solidne podstawy do uczenia się innych podejść.

Głęboka nauka $Q$

Algorytm, którego będziemy używać, został po raz pierwszy opisany w 2013 roku przez Mnih et al. w Granie na Atari z Deep Reinforcement Learning i dopracowane dwa lata później w kontroli na poziomie ludzkim poprzez głębokie uczenie ze wzmacnianiem. Wiele innych prac jest opartych na tych wynikach, w tym aktualny, najnowocześniejszy algorytm Rainbow (2017):

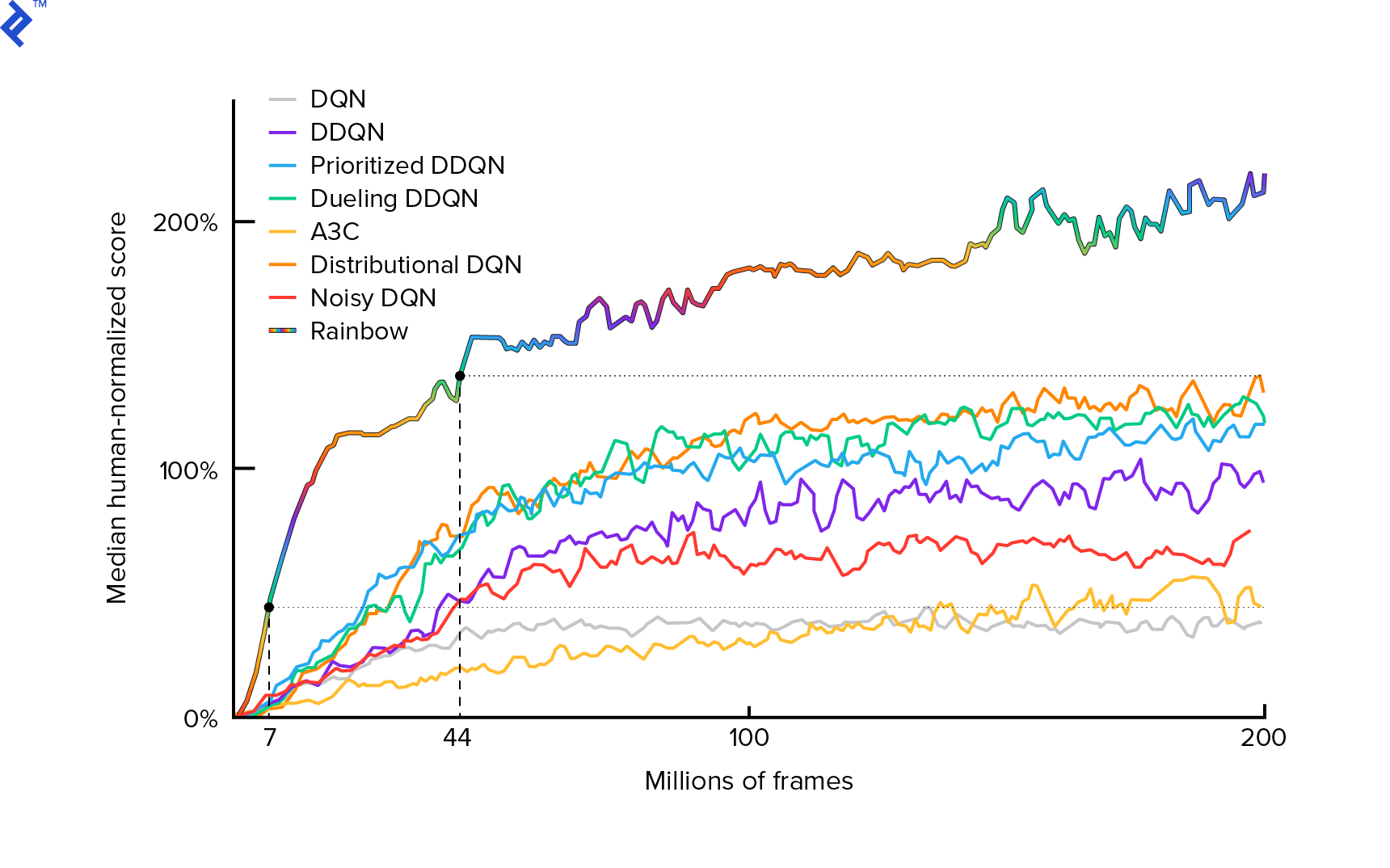
Rainbow osiąga nadludzką wydajność w wielu grach na Atari 2600. Skoncentrujemy się na podstawowej wersji DQN, z jak najmniejszą liczbą dodatkowych ulepszeń, aby utrzymać ten samouczek w rozsądnym rozmiarze.

Polityka, zwykle oznaczana $π(s)$, to funkcja zwracająca prawdopodobieństwa wykonania poszczególnych akcji w danym stanie $s$. Na przykład losowa polisa Mountain Car powraca dla dowolnego stanu: 50% w lewo, 50% w prawo. Podczas rozgrywki pobieramy próbki z tej polityki (dystrybucji), aby uzyskać realne działania.

$Q$-uczenie (Q oznacza Jakość) odnosi się do funkcji wartość-działania oznaczonej $Q_π(s, a)$. Zwraca całkowity zwrot z danego stanu $s$, wybierając akcję $a$, zgodnie z konkretną polityką $π$. Całkowity zwrot to suma wszystkich nagród w jednym odcinku (trajektorii).

Gdybyśmy znali optymalną funkcję $Q$, oznaczoną $Q^*$, moglibyśmy łatwo rozwiązać tę grę. Po prostu podążalibyśmy za działaniami o najwyższej wartości $Q^*$, tj. o najwyższym oczekiwanym zwrocie. To gwarantuje, że osiągniemy najwyższy możliwy zwrot.

Jednak często nie znamy $Q^*$. W takich przypadkach możemy ją przybliżyć – lub „uczyć się” – na podstawie interakcji z otoczeniem. To jest część nazwy „$Q$-learning”. Jest w nim również słowo „głębokie”, ponieważ do aproksymacji tej funkcji użyjemy głębokich sieci neuronowych, które są uniwersalnymi aproksymatorami funkcji. Głębokie sieci neuronowe, które przybliżają wartości $Q$, nazwano Deep Q-Networks (DQN). W prostych środowiskach (z liczbą stanów mieszczących się w pamięci) można po prostu użyć tabeli zamiast sieci neuronowej do reprezentowania funkcji $Q$, w którym to przypadku nazwano by ją „tabelaryczną nauką $Q$”.

Naszym celem jest teraz przybliżenie funkcji $Q^*$. Użyjemy równania Bellmana:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ to stan po $s$. $γ$ (gamma), zwykle 0,99, jest współczynnikiem dyskontowym (jest to hiperparametr). Przywiązuje mniejszą wagę do przyszłych nagród (ponieważ są one mniej pewne niż natychmiastowe nagrody z naszym niedoskonałym $Q$). Równanie Bellmana ma kluczowe znaczenie dla głębokiego uczenia się $Q$. Mówi, że $Q$-value dla danego stanu i działania jest nagrodą $r$ otrzymaną po wykonaniu działania $a$ plus najwyższa wartość $Q$ dla stanu, w którym wylądowaliśmy w $s'$. Najwyższy jest w pewnym sensie, że wybieramy akcję $a'$, która prowadzi do najwyższego całkowitego zwrotu z $s'$.

Za pomocą równania Bellmana możemy wykorzystać uczenie nadzorowane do przybliżenia $Q^*$. Funkcja $Q$ będzie reprezentowana (sparametryzowana) przez wagi sieci neuronowych oznaczone jako $θ$ (theta). Prosta implementacja wymagałaby stanu i działania jako wejścia i wyjścia wartości Q. Nieefektywność polega na tym, że jeśli chcemy poznać wartości $Q$ dla wszystkich akcji w danym stanie, musimy wywoływać $Q$ tyle razy, ile jest akcji. Jest o wiele lepszy sposób: wziąć tylko stan jako wartości wejściowe i wyjściowe $Q$ dla wszystkich możliwych działań. Dzięki temu możemy uzyskać wartości $Q$ dla wszystkich akcji w jednym przejściu do przodu.

Trening sieci $Q$ zaczynamy od losowych wag. Ze środowiska uzyskujemy wiele przejść (lub „doświadczeń”). Są to krotki (stan, akcja, następny stan, nagroda) lub w skrócie ($s$, $a$, $s'$, $r$). Przechowujemy ich tysiące w buforze pierścieniowym zwanym „powtórką doświadczeń”. Następnie próbkujemy doświadczenia z tego bufora z pragnieniem, aby zachowało się dla nich równanie Bellmana. Mogliśmy pominąć bufor i zastosować doświadczenia jeden po drugim (nazywa się to „online” lub „on-policy”); problem polega na tym, że kolejne doświadczenia są ze sobą silnie skorelowane, a DQN słabo trenuje, gdy to nastąpi. Dlatego wprowadzono powtórkę doświadczeń (podejście „offline”, „off-policy”), aby wydobyć tę korelację danych. Kod naszej najprostszej implementacji bufora pierścieniowego można znaleźć w pliku replay_buffer.py , zachęcam do zapoznania się z nim.

Na początku, ponieważ wagi naszych sieci neuronowych były losowe, wartość po lewej stronie równania Bellmana będzie daleka od prawej strony. Różnica do kwadratu będzie naszą funkcją straty. Zminimalizujemy funkcję strat, zmieniając wagi sieci neuronowej $θ$. Zapiszmy naszą funkcję straty:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

To przepisane równanie Bellmana. Załóżmy, że próbkowaliśmy doświadczenie ($s$, po lewej, $s'$, -1) z powtórki z Mountain Car. Wykonujemy przejście do przodu przez naszą sieć $Q$ ze stanem $s$ i za pozostałą akcję daje nam na przykład -120. Zatem $Q(s, \textrm{left}) = -120$. Następnie wrzucamy $s'$ do sieci, co daje nam np. -130 dla lewej i -122 dla prawej. Najwyraźniej najlepsza akcja dla $s'$ jest prawidłowa, stąd $\textrm{max}_{a'}Q(s', a') = -122$. Znamy $r$, to jest prawdziwa nagroda, która wynosiła -1. Więc nasza prognoza $Q$-sieci była nieco błędna, ponieważ $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Propagujemy więc błąd wstecz i nieznacznie poprawiamy wagi $θ$. Gdybyśmy mieli ponownie obliczyć stratę dla tego samego doświadczenia, byłaby ona teraz niższa.

Jedna ważna uwaga, zanim przejdziemy do kodu. Zauważmy, że aby zaktualizować nasz DQN, wykonamy dwa podania do przodu na samym DQN…. To często prowadzi do niestabilnego uczenia się. Aby to złagodzić, dla prognozy $Q$ następnego stanu nie używamy tego samego DQN. Używamy starszej wersji, która w kodzie nazywa się target_model (zamiast model , będący głównym DQN). Dzięki temu mamy stabilny cel. Aktualizujemy target_model , ustawiając go na wagi model co 1000 kroków. Ale model aktualizuje się na każdym kroku.

Spójrzmy na kod tworzący model DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Po pierwsze, funkcja pobiera wymiary akcji i przestrzeni obserwacji z danego środowiska OpenAI Gym. Trzeba na przykład wiedzieć, ile wyjść będzie miała nasza sieć. Musi być równa liczbie akcji. Akcje są zakodowane na gorąco:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Tak więc (np.) lewy będzie [1, 0], a prawy będzie [0, 1].

Widzimy, że obserwacje są przekazywane jako dane wejściowe. Przekazujemy również action_mask jako drugie wejście. Czemu? Przy obliczaniu $Q(s,a)$ musimy znać wartość $Q$ tylko dla jednej akcji, a nie dla wszystkich. action_mask zawiera 1 dla akcji, które chcemy przekazać do wyjścia DQN. Jeśli action_mask ma 0 dla jakiejś akcji, to odpowiadająca jej wartość $Q$ zostanie wyzerowana na wyjściu. Robi to warstwa filtered_output . Jeśli chcemy mieć wszystkie wartości $Q$ (do obliczenia maksymalnego), możemy po prostu przekazać je wszystkie.

Kod używa keras.layers.Dense do zdefiniowania w pełni połączonej warstwy. Keras to biblioteka Pythona do abstrakcji wyższego poziomu w oparciu o TensorFlow. Pod maską Keras tworzy wykres TensorFlow z odchyleniami, prawidłową inicjalizacją wagi i innymi rzeczami niskiego poziomu. Mogliśmy po prostu użyć surowego TensorFlow do zdefiniowania wykresu, ale nie będzie to jednowierszowy.

Tak więc obserwacje są przekazywane do pierwszej warstwy ukrytej, z aktywacją ReLU (rektyfikowana jednostka liniowa). ReLU(x) to po prostu funkcja $\textrm{max}(0, x)$. Ta warstwa jest w pełni połączona z drugą identyczną hidden_2 . Warstwa wyjściowa sprowadza liczbę neuronów do liczby akcji. W końcu mamy filtered_output , który po prostu mnoży wynik przez action_mask .

Aby znaleźć wagi $θ$, użyjemy optymalizatora o nazwie „Adam” ze średnią kwadratową stratą błędów.

Mając model, możemy go użyć do przewidzenia wartości $Q$ dla danych obserwacji stanu:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Chcemy wartości $Q$ dla wszystkich akcji, więc action_mask jest wektorem jedynek.

Aby przeprowadzić właściwe szkolenie, użyjemy fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Partia zawiera BATCH_SIZE doświadczeń. next_q_values ​​to $Q(s, a)$. q_values ​​to $r + γ \space \textrm{max}_{a'}Q(s', a')$ z równania Bellmana. Akcje, które podjęliśmy, są zakodowane na gorąco i przekazywane jako action_mask do danych wejściowych podczas wywoływania model.fit() . $y$ to powszechna litera oznaczająca „cel” w nadzorowanym uczeniu się. Tutaj przekazujemy q_values ​​. Robię q_values[:. None] q_values[:. None] , aby zwiększyć wymiar tablicy, ponieważ musi on odpowiadać wymiarowi tablicy one_hot_actions . Nazywa się to notacją plastra, jeśli chcesz przeczytać więcej na ten temat.

Zwracamy stratę, aby zapisać ją w pliku dziennika TensorBoard i później zwizualizować. Jest jeszcze wiele innych rzeczy, które będziemy monitorować: ile wykonujemy kroków na sekundę, całkowite zużycie pamięci RAM, jaki jest średni zwrot epizodów itp. Zobaczmy te wykresy.

Działanie

Aby zwizualizować plik dziennika TensorBoard, najpierw musimy go mieć. Więc po prostu poprowadźmy szkolenie:

 python run.py

To najpierw wydrukuje podsumowanie naszego modelu. Następnie utworzy katalog logów z aktualną datą i rozpocznie szkolenie. Co 2000 kroków zostanie wydrukowany logline podobny do tego:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Co 20 000 ocenimy nasz model na 10 000 kroków:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Po 677 odcinkach i 120 000 kroków średni powrót odcinka poprawił się z -200 do -136,75! To zdecydowanie się uczy. Czym jest avg_max_q_value , które zostawiam czytelnikowi jako dobre ćwiczenie. Ale jest to bardzo przydatna statystyka, na którą można patrzeć podczas treningu.

Po 200 000 kroków nasz trening dobiegł końca. Na moim czterordzeniowym procesorze zajmuje to około 20 minut. Możemy zajrzeć do katalogu date-log , np. 06-07-18-39-log . Będą cztery pliki modeli z rozszerzeniem .h5 . To jest migawka wag wykresów TensorFlow, zapisujemy je co 50 000 kroków, aby później przyjrzeć się polityce, której się nauczyliśmy. Aby go zobaczyć:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Aby zobaczyć inne możliwe flagi: python run.py --help .

Teraz samochód znacznie lepiej radzi sobie z osiągnięciem upragnionego celu. W katalogu date-log znajduje się również plik events.out.* . Jest to plik, w którym TensorBoard przechowuje swoje dane. Piszemy do niego za pomocą najprostszego TensorBoardLogger zdefiniowanego w loggers.py. Aby wyświetlić plik zdarzeń, musimy uruchomić lokalny serwer TensorBoard:

 tensorboard --logdir=.

--logdir wskazuje po prostu katalog, w którym znajdują się katalogi z datami, w naszym przypadku będzie to katalog bieżący, więc . . TensorBoard drukuje adres URL, pod którym nasłuchuje. Jeśli otworzysz http://127.0.0.1:6006, powinieneś zobaczyć osiem wykresów podobnych do tych:

Zawijanie

train() wykonuje całe szkolenie. Najpierw tworzymy model i odtwarzamy bufor. Następnie w pętli bardzo podobnej do tej z see.py wchodzimy w interakcję ze środowiskiem i przechowujemy doświadczenia w buforze. Co ważne, postępujemy zgodnie z polityką epsilon-greedy. Zawsze możemy wybrać najlepszą akcję zgodnie z funkcją $Q$; to jednak zniechęca do eksploracji, co szkodzi ogólnej wydajności. Aby więc wymusić eksplorację z prawdopodobieństwem epsilon, wykonujemy losowe działania:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon ustawiono na 1%. Po 2000 doświadczeniach powtórka zapełnia się na tyle, aby rozpocząć trening. Robimy to, wywołując fit_batch() z losową partią doświadczeń pobraną z bufora powtórek:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Co 20 000 kroków oceniamy i rejestrujemy wyniki (ocena jest z epsilon = 0 , całkowicie zachłanna polityka):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

Cały kod to około 300 linii, a run.py zawiera około 250 najważniejszych.

Można zauważyć wiele hiperparametrów:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

A to nawet nie wszystkie. Jest też architektura sieciowa — użyliśmy dwóch ukrytych warstw z 32 neuronami, aktywacjami ReLU i optymalizatorem Adam, ale jest wiele innych opcji. Nawet drobne zmiany mogą mieć ogromny wpływ na trening. Można poświęcić dużo czasu na dostrajanie hiperparametrów. W niedawnym konkursie OpenAI zawodnik, który zajął drugie miejsce, odkrył, że możliwe jest prawie podwojenie wyniku Rainbow po dostrojeniu hiperparametrów. Oczywiście trzeba pamiętać, że łatwo się przerobić. Obecnie algorytmy wzmacniające zmagają się z transferem wiedzy do podobnych środowisk. Nasz samochód górski nie uogólnia obecnie wszystkich rodzajów gór. Możesz faktycznie zmodyfikować środowisko OpenAI Gym i zobaczyć, jak daleko agent może uogólniać.

Kolejnym ćwiczeniem będzie znalezienie lepszego zestawu hiperparametrów niż mój. To na pewno możliwe. Jednak jeden bieg treningowy nie wystarczy, aby ocenić, czy Twoja zmiana jest poprawą. Zwykle jest duża różnica między biegami treningowymi; wariancja jest duża. Potrzebujesz wielu przebiegów, aby stwierdzić, że coś jest lepsze. Jeśli chciałbyś przeczytać więcej na tak ważny temat, jak odtwarzalność, zachęcam do lektury Deep Reinforcement Learning that Matters. Zamiast ręcznie dostrajać, możemy do pewnego stopnia zautomatyzować ten proces — jeśli chcemy wydać więcej mocy obliczeniowej na rozwiązanie problemu. Prostym podejściem jest przygotowanie obiecującego zakresu wartości dla niektórych hiperparametrów, a następnie przeszukanie siatki (sprawdzenie ich kombinacji) z równoległymi treningami. Sama równoległość jest dużym tematem, ponieważ ma kluczowe znaczenie dla wysokiej wydajności.

Głębokie uczenie $Q$ reprezentuje dużą rodzinę algorytmów uczenia się ze wzmocnieniem, które wykorzystują iterację wartości. Próbowaliśmy aproksymować funkcję $Q$ i przez większość czasu używaliśmy jej po prostu zachłannie. Istnieje inna rodzina, która używa iteracji zasad. Nie skupiają się na aproksymacji funkcji $Q$, ale na bezpośrednim znalezieniu optymalnej strategii $π^*$. Aby zobaczyć, gdzie iteracja wartości pasuje do krajobrazu algorytmów uczenia przez wzmacnianie:

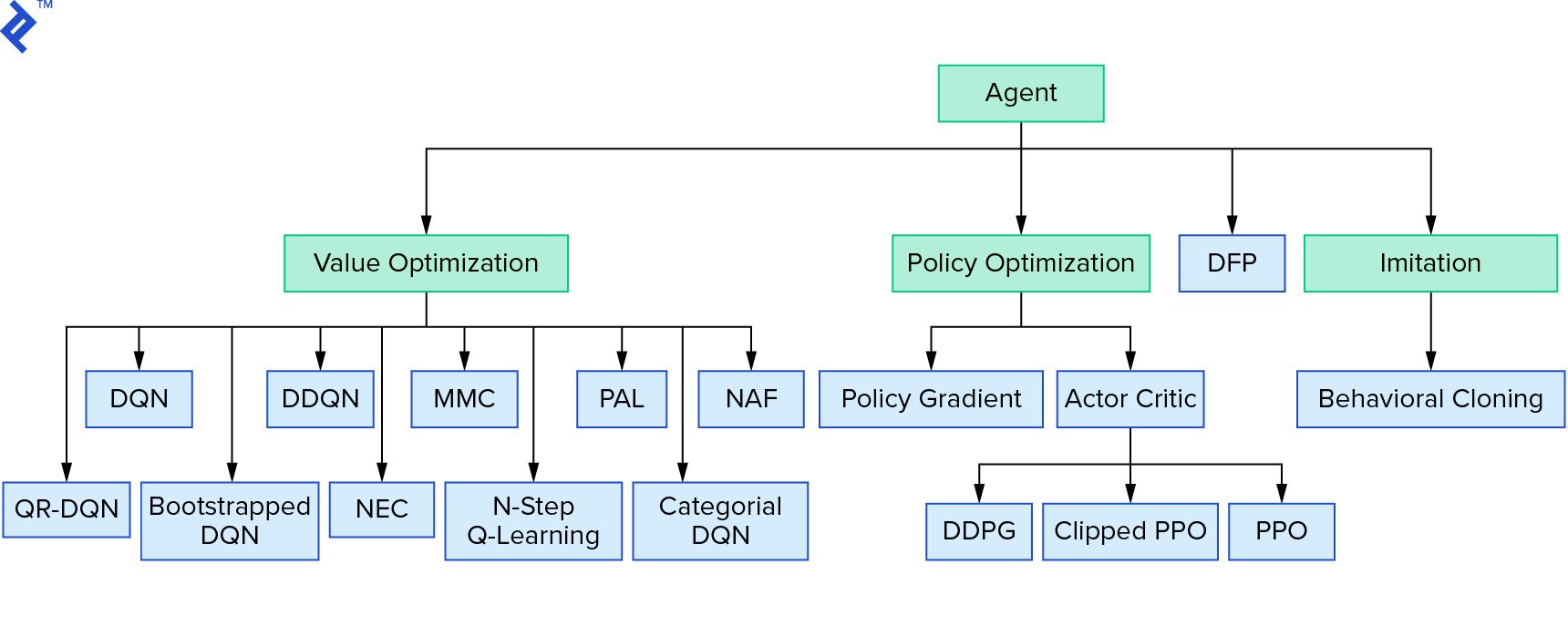
Twoje myśli mogą być takie, że uczenie się przez głębokie wzmocnienie wygląda na kruche. Będziesz miał rację; jest wiele problemów. Możesz odnieść się do Głębokiego uczenia się ze wzmacnianiem jeszcze nie działa, a uczenie się ze wzmacnianiem nigdy nie zadziałało, a „głębokie” tylko trochę pomogło.

To kończy samouczek. Wdrożyliśmy własny podstawowy DQN do celów edukacyjnych. Bardzo podobny kod można wykorzystać do uzyskania dobrej wydajności w niektórych grach na Atari. W zastosowaniach praktycznych często bierze się sprawdzone, wysokowydajne implementacje, np. jedną z baz OpenAI. Jeśli chcesz zobaczyć, z jakimi wyzwaniami można się zmierzyć, próbując zastosować głębokie uczenie ze wzmocnieniem w bardziej złożonym środowisku, przeczytaj Nasze NIPS 2017: podejście do nauki biegania. Jeśli chcesz dowiedzieć się więcej w zabawnym środowisku konkursowym, zajrzyj na konkursy NIPS 2018 lub crowdai.org.

Jeśli jesteś na dobrej drodze do zostania ekspertem w dziedzinie uczenia maszynowego i chcesz pogłębić swoją wiedzę w uczeniu nadzorowanym, zapoznaj się z Machine Learning Video Analysis: Identyfikowanie ryb , aby przeprowadzić zabawny eksperyment dotyczący identyfikacji ryb.