深入了解强化学习
已发表: 2022-03-11让我们深入了解强化学习。 在本文中,我们将解决 TensorFlow、TensorBoard、Keras 和 OpenAI gym 等现代库的具体问题。 您将看到如何实现一种称为深度 $Q$-learning 的基本算法来了解其内部工作原理。 关于硬件,整个代码将在典型的 PC 上运行并使用所有找到的 CPU 内核(这由 TensorFlow 开箱即用地处理)。
这个问题被称为山车:一辆汽车在一维轨道上,位于两座山之间。 目标是在右边开车上山(到达国旗)。 但是,这辆车的发动机不够强大,无法单程爬山。 因此,成功的唯一方法是来回驱动以积蓄动力。
选择这个问题是因为它很简单,可以在几分钟内在单个 CPU 内核上找到强化学习的解决方案。 但是,它足够复杂,无法成为一个好的代表。
首先,我将简要总结一下强化学习的一般作用。 然后,我们将介绍基本术语并表达我们对它们的问题。 之后,我将描述深度 $Q$ 学习算法,我们将实施它来解决问题。
强化学习基础
用最简单的话来说,强化学习就是通过反复试验来学习。 主角被称为“代理人”,这将是我们问题中的汽车。 智能体在环境中做出动作,并获得新的观察结果和对该动作的奖励。 导致更大回报的行动得到加强,因此得名。 与计算机科学中的许多其他事情一样,这一点也受到观察生物的启发。
下图总结了代理与环境的交互:
代理会因执行的操作而获得观察和奖励。 然后它进行另一个动作并执行第二步。 环境现在返回(可能)略有不同的观察和奖励。 这一直持续到达到终端状态,通过向代理发送“完成”来发出信号。 观察 > 动作 > next_observations > 奖励的整个序列称为情节(或轨迹)。
回到我们的山地车:我们的车是代理。 环境是一维山脉的黑箱世界。 汽车的动作归结为只有一个数字:如果是正数,则发动机将汽车推向右侧。 如果为负,则将汽车向左推。 代理通过观察来感知环境:汽车的 X 位置和速度。 如果我们希望我们的汽车在山顶上行驶,我们以一种方便的方式定义奖励:代理在它没有达到目标的每一步中获得 -1 的奖励。 当它达到目标时,这一集就结束了。 所以,事实上,代理人因为没有处于我们想要的位置而受到惩罚。 他越快到达它,对他就越好。 代理的目标是最大化总奖励,这是一个情节的奖励总和。 因此,如果它在例如 110 步之后到达期望的点,它会收到 -110 的总回报,这对于 Mountain Car 来说将是一个很好的结果,因为如果它没有达到目标,那么它会被惩罚 200 步(因此,返回 -200)。
这是整个问题的表述。 现在,我们可以把它交给算法,这些算法已经足够强大,可以在几分钟内解决这些问题(如果调整得当的话)。 值得注意的是,我们并没有告诉代理如何实现目标。 我们甚至不提供任何提示(启发式)。 代理人将找到一种方式(政策)以自己获胜。
设置环境
首先,将整个教程代码复制到您的磁盘上:
git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial现在,我们需要安装我们将使用的 Python 包。 为了不将它们安装在您的用户空间中(并有冲突的风险),我们将使其干净并将它们安装在 conda 环境中。 如果您没有安装 conda,请按照 https://conda.io/docs/user-guide/install/index.html 操作。
创建我们的 conda 环境:
conda create -n tutorial python=3.6.5 -y要激活它:
source activate tutorial 您应该在 shell 的提示符附近看到(tutorial) 。 这意味着名为“tutorial”的 conda 环境处于活动状态。 从现在开始,所有命令都应该在该 conda 环境中执行。
现在,我们可以在密封 conda 环境中安装所有依赖项:
pip install -r requirements.txt我们已经完成了安装,所以让我们运行一些代码。 我们不需要自己实现 Mountain Car 环境; OpenAI Gym 库提供了该实现。 让我们看看我们环境中的一个随机代理(一个采取随机动作的代理):
import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render() 这是see.py文件; 要运行它,请执行:
python see.py你应该看到一辆汽车随机来回行驶。 每集将包含 200 个步骤; 总回报将是-200。
现在我们需要用更好的东西替换随机动作。 有很多算法可以使用。 对于介绍性教程,我认为一种称为深度 $Q$-learning 的方法非常适合。 理解该方法为学习其他方法奠定了坚实的基础。
深度$Q$-学习
我们将使用的算法于 2013 年由 Mnih 等人首次描述。 在用深度强化学习玩 Atari 并在两年后通过深度强化学习在人类水平控制方面进行了打磨。 许多其他工作都建立在这些结果之上,包括当前最先进的算法 Rainbow(2017):
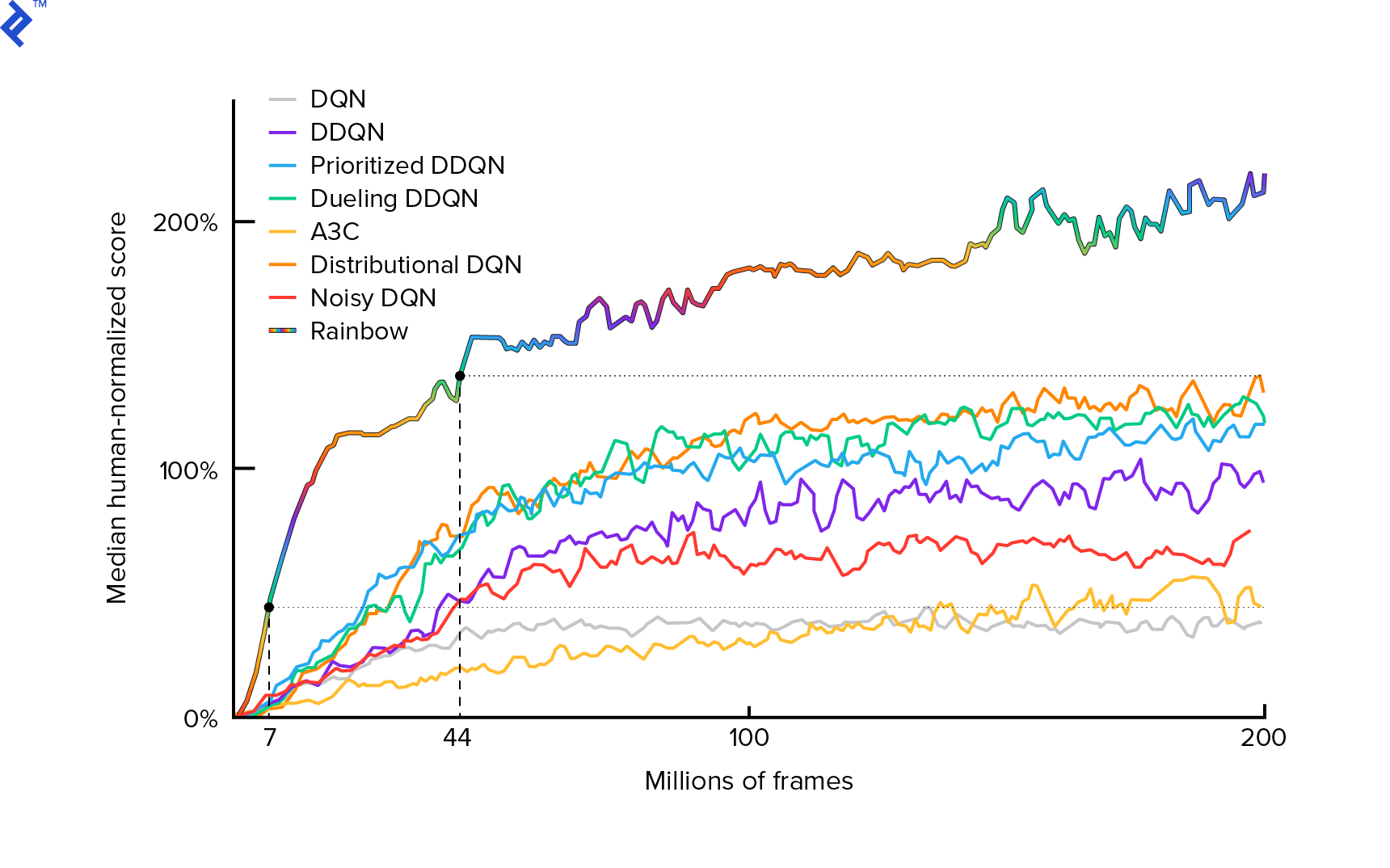
Rainbow 在许多 Atari 2600 游戏中实现了超人的性能。 我们将专注于基本的 DQN 版本,并尽可能少地进行一些额外的改进,以使本教程保持合理的大小。
策略,通常表示为 $π(s)$,是一个函数,它返回在给定状态 $s$ 中采取个人行动的概率。 因此,例如,对于任何状态,随机 Mountain Car 策略都会返回:50% 左,50% 右。 在游戏过程中,我们从该策略(分布)中采样以获得实际动作。
$Q$-learning(Q 代表质量)指的是表示为 $Q_π(s,a)$ 的动作价值函数。 它返回给定状态 $s$ 的总回报,选择动作 $a$,遵循具体策略 $π$。 总回报是一集(轨迹)中所有奖励的总和。
如果我们知道最优的$Q$-函数,记为$Q^*$,我们可以很容易地解决这个游戏。 我们将只遵循具有最高价值 $Q^*$ 的行动,即最高预期回报。 这保证了我们将获得尽可能高的回报。
然而,我们常常不知道$Q^*$。 在这种情况下,我们可以从与环境的交互中近似或“学习”它。 这是名称中的“$Q$-learning”部分。 其中还有“深度”一词,因为为了逼近该函数,我们将使用深度神经网络,它是通用函数逼近器。 近似 $Q$-values 的深度神经网络被命名为 Deep Q-Networks (DQN)。 在简单的环境中(状态数适合内存),可以只使用表格而不是神经网络来表示 $Q$-函数,在这种情况下,它将被命名为“表格 $Q$-learning”。
所以我们现在的目标是逼近 $Q^*$ 函数。 我们将使用贝尔曼方程:
\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]$s'$ 是 $s$ 之后的状态。 $γ$ (gamma),通常为 0.99,是一个折扣因子(它是一个超参数)。 它对未来奖励的权重较小(因为它们比我们不完美的 $Q$ 的即时奖励更不确定)。 贝尔曼方程是深度 $Q$ 学习的核心。 它表示给定状态和动作的 $Q$-value 是在采取行动 $a$ 后收到的奖励 $r$加上我们在 $s'$ 所在状态的最高 $Q$-value。 从某种意义上说,最高的是我们正在选择一个动作$a'$,这导致$s'$的总回报最高。
通过贝尔曼方程,我们可以使用监督学习来逼近 $Q^*$。 $Q$ 函数将由表示为 $θ$ (theta) 的神经网络权重表示(参数化)。 一个简单的实现会将一个状态和一个动作作为网络输入并输出 Q 值。 效率低下的是,如果我们想知道给定状态下所有动作的 $Q$-values,我们需要调用 $Q$ 的次数与动作的次数一样多。 有一个更好的方法:只将状态作为输入并为所有可能的操作输出 $Q$-values。 多亏了这一点,我们可以在一次前向传递中获得所有动作的 $Q$-values。
我们开始用随机权重训练 $Q$ 网络。 从环境中,我们获得了许多转变(或“经验”)。 这些是 (state, action, next state, reward) 的元组,或者简而言之,是 ($s$, $a$, $s'$, $r$)。 我们将数千个它们存储在一个称为“体验重放”的环形缓冲区中。 然后,我们从该缓冲区中采样经验,希望贝尔曼方程适用于他们。 我们可以跳过缓冲区并一个一个地应用经验(这被称为“在线”或“on-policy”); 问题是随后的经验彼此高度相关,并且当这种情况发生时,DQN 训练很差。 这就是为什么引入体验回放(一种“离线”、“离线”方法)来打破这种数据相关性。 我们最简单的环形缓冲区实现的代码可以在replay_buffer.py文件中找到,我鼓励你阅读它。
一开始,由于我们的神经网络权重是随机的,贝尔曼方程的左侧值将远离右侧。 平方差将是我们的损失函数。 我们将通过改变神经网络权重 $θ$ 来最小化损失函数。 让我们写下我们的损失函数:
\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]这是一个重写的贝尔曼方程。 假设我们从 Mountain Car 体验回放中采样了一次体验($s$, left, $s'$, -1)。 例如,我们通过状态为 $s$ 的 $Q$ 网络进行前向传递,对于左侧的动作,它给我们 -120。 所以,$Q(s, \textrm{left}) = -120$。 然后我们将 $s'$ 输入到网络中,这给了我们,例如,左侧为 -130,右侧为 -122。 很明显,$s'$ 的最佳操作是正确的,因此 $\textrm{max}_{a'}Q(s', a') = -122$。 我们知道$r$,这是真正的奖励,是-1。 所以我们的 $Q$-network 预测有点错误,因为 $L(θ) = [-120 - 1 + 0.99 ⋅ 122]^2 = (-0.22^2) = 0.0484$。 所以我们向后传播误差并稍微修正权重$θ$。 如果我们要再次计算相同体验的损失,现在它会更低。
在我们开始编码之前的一个重要观察。 让我们注意,为了更新我们的 DQN,我们将对 DQN 本身进行两次前向传递。 这通常会导致学习不稳定。 为了缓解这种情况,对于下一个状态 $Q$ 预测,我们不使用相同的 DQN。 我们使用它的旧版本,在代码中称为target_model (而不是model ,是主要的 DQN)。 多亏了这一点,我们有了一个稳定的目标。 我们通过将target_model设置为每 1000 步的model权重来更新它。 但是model每一步都会更新。
让我们看一下创建 DQN 模型的代码:
def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model首先,该函数从给定的 OpenAI Gym 环境中获取动作和观察空间的维度。 例如,有必要知道我们的网络将有多少输出。 它必须等于动作的数量。 动作是一种热编码:
def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot所以(例如)左边是[1, 0],右边是[0, 1]。
我们可以看到观察结果作为输入传递。 我们还将action_mask作为第二个输入传递。 为什么? 在计算 $Q(s,a)$ 时,我们只需要知道一个给定动作的 $Q$-value,而不是所有动作。 action_mask包含 1 表示我们要传递给 DQN 输出的操作。 如果action_mask的某个动作为 0,则相应的 $Q$-value 将在输出上归零。 filtered_output层就是这样做的。 如果我们想要所有的 $Q$ 值(用于最大值计算),我们可以传递所有的值。

代码使用keras.layers.Dense定义全连接层。 Keras 是一个 Python 库,用于在 TensorFlow 之上进行更高级别的抽象。 在底层,Keras 创建了一个 TensorFlow 图,其中包含偏差、适当的权重初始化和其他低级别的东西。 我们本可以只使用原始 TensorFlow 来定义图形,但它不会是单行的。
所以观察被传递到第一个隐藏层,带有 ReLU(校正线性单元)激活。 ReLU(x)只是一个 $\textrm{max}(0, x)$ 函数。 该层与第二个相同的层hidden_2 2 完全连接。 输出层将神经元的数量减少到动作的数量。 最后,我们得到了filtered_output ,它只是将输出与action_mask 。
为了找到 $θ$ 权重,我们将使用一个名为“Adam”的优化器,它具有均方误差损失。
有了一个模型,我们可以用它来预测给定状态观察的 $Q$ 值:
def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask]) 我们想要所有动作的 $Q$-values,因此action_mask是一个向量。
为了进行实际训练,我们将使用fit_batch() :
def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0] Batch 包含BATCH_SIZE体验。 next_q_values是 $Q(s, a)$。 q_values是来自贝尔曼方程的 $r + γ \space \textrm{max}_{a'}Q(s', a')$。 我们采取的行动是一种热编码,并在调用model.fit()时作为action_mask传递给输入。 $y$ 是监督学习中“目标”的常用字母。 这里我们传递q_values 。 我做q_values[:. None] q_values[:. None]增加数组维度,因为它必须对应于one_hot_actions数组的维度。 如果您想了解更多有关它的信息,这称为切片表示法。
我们返回损失以将其保存在 TensorBoard 日志文件中,然后进行可视化。 我们将监控许多其他事情:我们每秒执行多少步、总 RAM 使用量、平均剧集回报是多少等。让我们看看这些图。
跑步
为了可视化 TensorBoard 日志文件,我们首先需要一个。 所以让我们开始训练:
python run.py这将首先打印我们模型的摘要。 然后它将创建一个包含当前日期的日志目录并开始训练。 每 2000 步,将打印一条日志行,如下所示:
episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM每 20,000 次,我们将在 10,000 步上评估我们的模型:
Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004 在 677 集和 120,000 步之后,平均集回报从 -200 提高到 -136.75! 绝对是在学习。 什么avg_max_q_value是我留给读者的一个很好的练习。 但这是在训练期间查看的非常有用的统计数据。
200,000 步之后,我们的训练就完成了。 在我的四核 CPU 上,大约需要 20 分钟。 我们可以查看date-log目录,例如06-07-18-39-log 。 将有四个扩展名为.h5的模型文件。 这是 TensorFlow 图权重的快照,我们每 50,000 步保存一次,以便稍后查看我们学到的策略。 要查看它:
python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view 要查看其他可能的标志: python run.py --help 。
现在,汽车在达到预期目标方面做得更好。 在date-log目录中,还有events.out.*文件。 这是 TensorBoard 存储其数据的文件。 我们使用TensorBoardLogger中定义的最简单的 TensorBoardLogger 对其进行loggers.py. 要查看事件文件,我们需要运行本地 TensorBoard 服务器:
tensorboard --logdir=. --logdir只是指向包含日期日志目录的目录,在我们的例子中,这将是当前目录,所以. . TensorBoard 打印它正在侦听的 URL。 如果你打开 http://127.0.0.1:6006,你应该会看到八个类似的图:
包起来
train()完成所有训练。 我们首先创建模型并重放缓冲区。 然后,在与see.py中的循环非常相似的循环中,我们与环境交互并将体验存储在缓冲区中。 重要的是我们遵循 epsilon-greedy 策略。 我们总是可以根据 $Q$-function 选择最佳动作; 但是,这会阻碍探索,从而损害整体性能。 因此,为了使用 epsilon 概率进行探索,我们执行随机操作:
def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action Epsilon 设置为 1%。 在 2000 次体验之后,回放充满足以开始训练。 我们通过调用fit_batch()来实现,其中包含从重放缓冲区中采样的随机一批经验:
batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch) 每 20,000 步,我们评估并记录结果(评估是使用epsilon = 0 ,完全贪婪的策略):
if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step) 整个代码大约 300 行, run.py包含大约 250 个最重要的代码。
可以注意到有很多超参数:
DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000这甚至不是全部。 还有一个网络架构——我们使用了两个具有 32 个神经元的隐藏层、ReLU 激活和 Adam 优化器,但还有很多其他选项。 即使是很小的变化也会对培训产生巨大影响。 可以花费大量时间调整超参数。 在最近的 OpenAI 比赛中,一位获得第二名的选手发现,在超参数调优后,Rainbow 的分数几乎可以翻倍。 自然,人们必须记住,过拟合很容易。 目前,强化算法正在努力将知识转移到类似环境。 我们的 Mountain Car 目前还不能推广到所有类型的山脉。 你实际上可以修改 OpenAI Gym 环境,看看代理可以泛化到什么程度。
另一个练习是找到一组比我更好的超参数。 这绝对是可能的。 然而,一次训练并不足以判断你的改变是否是一种进步。 训练运行之间通常存在很大差异; 方差很大。 您需要多次运行才能确定某些东西更好。 如果您想了解更多关于可重复性等重要主题的信息,我鼓励您阅读重要的深度强化学习。 如果我们愿意在这个问题上花费更多的计算能力,我们可以在一定程度上自动化这个过程,而不是手动调整。 一种简单的方法是为一些超参数准备一个有希望的值范围,然后运行网格搜索(检查它们的组合),并行运行训练。 并行化本身就是一个很大的话题,因为它对高性能至关重要。
深度 $Q$-learning 代表了一大类使用值迭代的强化学习算法。 我们试图逼近 $Q$ 函数,但大多数时候我们只是以贪婪的方式使用它。 还有另一个家庭使用策略迭代。 他们不专注于逼近$Q$-函数,而是直接找到最优策略$π^*$。 要查看值迭代在强化学习算法领域中的位置:
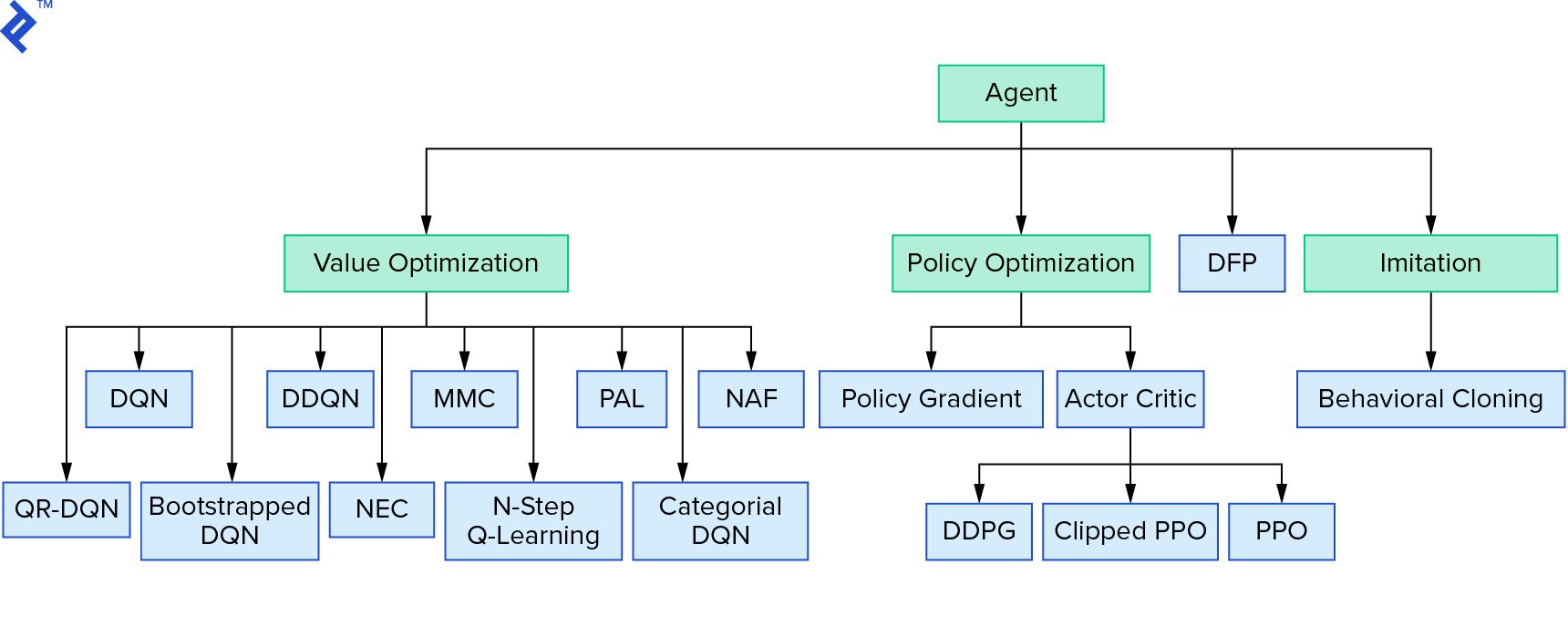
你的想法可能是深度强化学习看起来很脆弱。 你是对的; 有很多问题。 你可以参考 Deep Reinforcement Learning doesn't Work Yet 和 Reinforcement Learning never work ,而“deep”只是有点帮助。
教程到此结束。 为了学习目的,我们实现了自己的基本 DQN。 非常相似的代码可用于在某些 Atari 游戏中实现良好的性能。 在实际应用中,通常需要经过测试的高性能实现,例如来自 OpenAI 基线的一种。 如果您想了解在更复杂的环境中尝试应用深度强化学习时会面临哪些挑战,您可以阅读 Our NIPS 2017:Learning to Run 方法。 如果您想在有趣的比赛环境中了解更多信息,请查看 NIPS 2018 Competitions 或 crowdai.org。
如果您正在成为机器学习专家并希望加深您在监督学习方面的知识,请查看机器学习视频分析:识别鱼,了解有关识别鱼的有趣实验。
