Takviyeli Öğrenmeye Derin Bir Bakış

Haydi pekiştirmeli öğrenmeye derin bir dalış yapalım. Bu makalede, TensorFlow, TensorBoard, Keras ve OpenAI gym gibi modern kütüphanelerle ilgili somut bir sorunu ele alacağız. Derin $Q$-öğrenme adı verilen temel algoritmalardan birinin nasıl uygulanacağını ve iç işleyişini öğreneceğinizi göreceksiniz. Donanımla ilgili olarak, kodun tamamı tipik bir bilgisayarda çalışacak ve bulunan tüm CPU çekirdeklerini kullanacak (bu, kutudan çıktığı gibi TensorFlow tarafından gerçekleştirilir).

Sorunun adı Dağ Arabası: Bir araba, iki dağ arasında konumlanmış tek boyutlu bir yolda. Amaç, sağdaki dağa çıkmak (bayrağa ulaşmak). Ancak otomobilin motoru tek geçişte dağa tırmanacak kadar güçlü değil. Bu nedenle, başarılı olmanın tek yolu, momentum oluşturmak için ileri geri gitmektir.

Bu problem, tek bir CPU çekirdeğinde dakikalar içinde pekiştirmeli öğrenme ile bir çözüm bulmak için yeterince basit olduğu için seçilmiştir. Ancak, iyi bir temsilci olmak için yeterince karmaşıktır.

İlk olarak, pekiştirmeli öğrenmenin genel olarak ne yaptığının kısa bir özetini vereceğim. Daha sonra temel terimlere değineceğiz ve bunlarla ilgili sorunumuzu dile getireceğiz. Ondan sonra, derin $Q$-öğrenme algoritmasını anlatacağım ve problemi çözmek için onu uygulayacağız.

Pekiştirmeli Öğrenme Temelleri

En basit ifadeyle pekiştirmeli öğrenme, deneme yanılma yoluyla öğrenmedir. Ana karaktere, sorunumuzda bir araba olacak olan “ajan” denir. Etmen bir ortamda bir eylemde bulunur ve kendisine yeni bir gözlem ve bu eylem için bir ödül verilir. Daha büyük ödüllere yol açan eylemler güçlendirilir, bu nedenle adı. Bilgisayar bilimindeki diğer pek çok şey gibi, bu da canlı yaratıkları gözlemlemekten ilham aldı.

Aracının bir ortamla etkileşimleri aşağıdaki grafikte özetlenmiştir:

Temsilci, gerçekleştirilen eylem için bir gözlem ve ödül alır. Sonra başka bir işlem yapar ve ikinci adımı atar. Çevre şimdi (muhtemelen) biraz farklı bir gözlem ve ödül veriyor. Bu, bir aracıya "bitti" mesajı gönderilerek sinyal verilen terminal durumuna ulaşılana kadar devam eder. Tüm gözlemler > eylemler > sonraki_gözlemler > ödüller dizisine bölüm (veya yörünge) denir.

Dağ Arabamıza geri dönersek: arabamız bir acentedir. Çevre, tek boyutlu dağların kara kutu dünyasıdır. Arabanın hareketi yalnızca bir sayıya indirgenir: pozitifse, motor arabayı sağa doğru iter. Negatif ise, arabayı sola doğru iter. Aracı, bir gözlem yoluyla bir ortamı algılar: arabanın X konumu ve hızı. Arabamızın dağın tepesinde gitmesini istiyorsak, ödülü uygun bir şekilde tanımlarız: Temsilci, hedefe ulaşmadığı her adım için ödülüne -1 alır. Hedefe ulaştığında, bölüm sona erer. Yani aslında ajan bizim istediğimiz pozisyonda olmadığı için cezalandırılıyor. Ne kadar hızlı ulaşırsa onun için o kadar iyi. Temsilcinin amacı, bir bölümdeki ödüllerin toplamı olan toplam ödülü maksimize etmektir. Yani örneğin 110 adımdan sonra istenilen noktaya ulaşırsa toplam -110 dönüş alır ki bu Dağ Arabası için harika bir sonuç olur çünkü hedefe ulaşamazsa 200 adım cezalandırılır. (dolayısıyla -200'lük bir dönüş).

Bütün problem formülasyonu budur. Şimdi, bu tür sorunları dakikalar içinde (iyi ayarlanmışsa) çözecek kadar güçlü olan algoritmalara verebiliriz. Temsilciye hedefe nasıl ulaşacağını söylemediğimizi belirtmekte fayda var. Herhangi bir ipucu bile sağlamıyoruz (sezgisel). Temsilci kendi başına kazanmanın bir yolunu (politika) bulacaktır.

Ortamın Ayarlanması

İlk önce, eğitim kodunun tamamını diskinize kopyalayın:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Şimdi kullanacağımız Python paketlerini kurmamız gerekiyor. Bunları kullanıcı alanınıza kurmamak için (ve çarpışma riski), onu temizleyeceğiz ve conda ortamına kuracağız. Conda kurulu değilse, lütfen https://conda.io/docs/user-guide/install/index.html adresini takip edin.

Conda ortamımızı oluşturmak için:

 conda create -n tutorial python=3.6.5 -y

Etkinleştirmek için:

 source activate tutorial

Kabukta isteminizin yanında (tutorial) görmelisiniz. Bu, “tutorial” adlı bir conda ortamının aktif olduğu anlamına gelir. Şu andan itibaren, tüm komutlar o conda ortamında yürütülmelidir.

Artık hermetik conda ortamımıza tüm bağımlılıkları kurabiliriz:

 pip install -r requirements.txt

Kurulumu bitirdik, şimdi biraz kod çalıştıralım. Dağ Arabası ortamını kendi başımıza uygulamamıza gerek yok; OpenAI Gym kütüphanesi bu uygulamayı sağlar. Ortamımızdaki rastgele bir aracıyı (rastgele eylemler gerçekleştiren bir aracı) görelim:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Bu, see.py dosyasıdır; çalıştırmak için yürütün:

 python see.py

Rastgele ileri geri giden bir araba görmelisiniz. Her bölüm 200 adımdan oluşacak; toplam getiri -200 olacaktır.

Şimdi rastgele eylemleri daha iyi bir şeyle değiştirmemiz gerekiyor. Kullanılabilecek birçok algoritma var. Bir giriş eğitimi için, derin $Q$-öğrenme adlı bir yaklaşımın iyi bir uyum olduğunu düşünüyorum. Bu yöntemi anlamak, diğer yaklaşımları öğrenmek için sağlam bir temel sağlar.

Derin $Q$-öğrenme

Kullanacağımız algoritma ilk olarak 2013 yılında Mnih ve ark. Atari'yi Derin Takviyeli Öğrenme ile Oynama'da ve iki yıl sonra derin pekiştirmeli öğrenme yoluyla İnsan düzeyinde kontrolde cilalandı. Mevcut en son algoritma Rainbow (2017) dahil olmak üzere, bu sonuçlar üzerine birçok başka çalışma yapılmıştır:

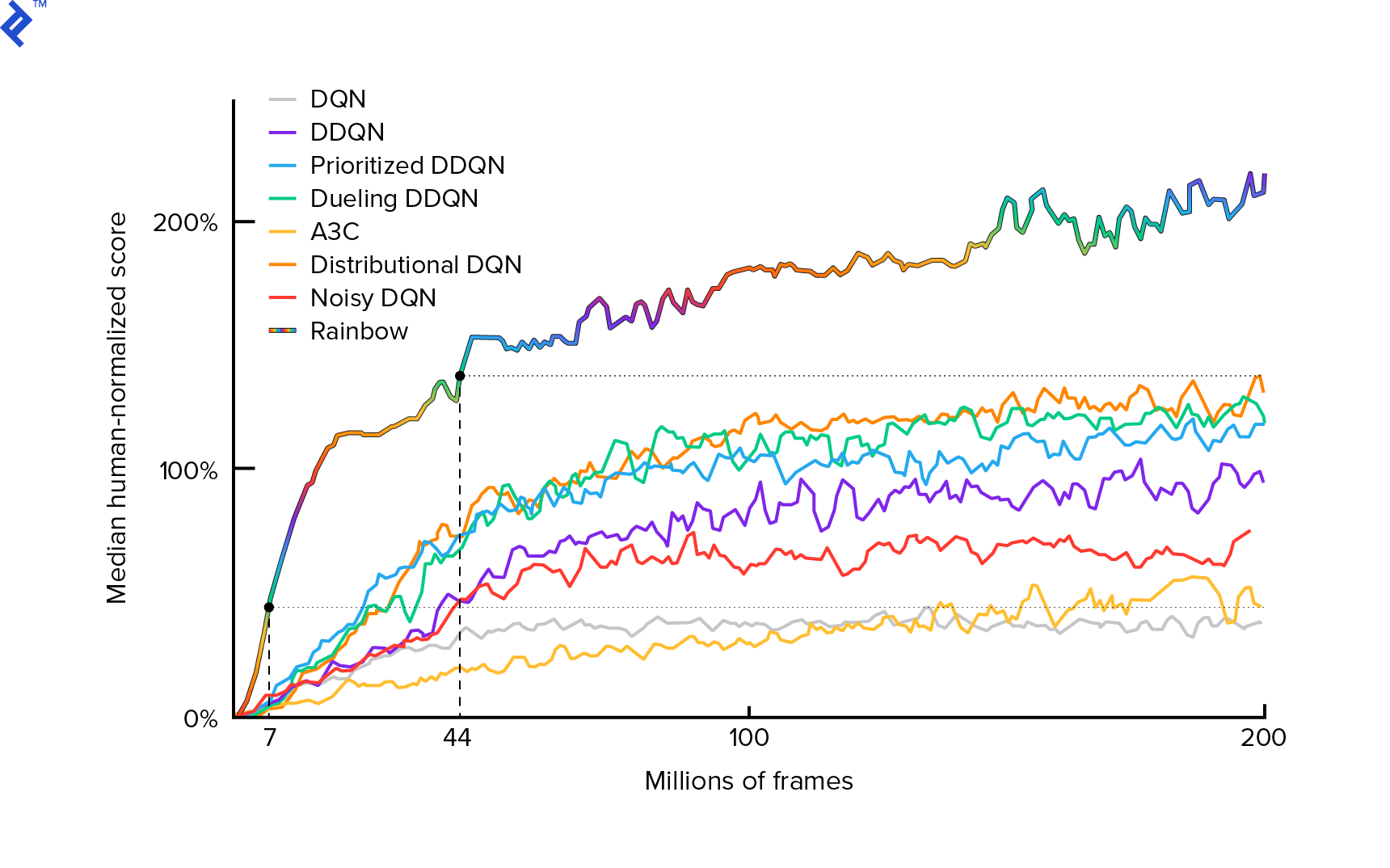
Rainbow, birçok Atari 2600 oyununda insanüstü performans elde ediyor. Bu öğreticiyi makul bir boyutta tutmak için mümkün olduğunca az sayıda ek iyileştirme ile temel DQN sürümüne odaklanacağız.

Tipik olarak $π(s)$ ile gösterilen bir politika, belirli bir $s$ durumunda bireysel eylemleri gerçekleştirme olasılıklarını döndüren bir fonksiyondur. Örneğin, herhangi bir durum için rastgele bir Dağ Arabası politikası döner: %50 sol, %50 sağ. Oyun sırasında, gerçek eylemleri elde etmek için bu politikadan (dağıtımdan) örnekler alırız.

$Q$-öğrenme (Q, Kalite içindir), $Q_π(s, a)$ ile gösterilen eylem-değer işlevine atıfta bulunur. Somut bir $π$ politikasını izleyerek, $a$ eylemini seçerek belirli bir $s$ durumundan toplam getiriyi döndürür. Toplam getiri, bir bölümdeki (yörüngedeki) tüm ödüllerin toplamıdır.

$Q^*$ ile gösterilen optimal $Q$-işlevini bilseydik, oyunu kolayca çözebilirdik. Sadece en yüksek $Q^*$ değerine sahip, yani beklenen en yüksek getiriye sahip eylemleri takip ederdik. Bu, mümkün olan en yüksek getiriye ulaşacağımızı garanti eder.

Ancak, genellikle $Q^*$'ı bilmiyoruz. Bu gibi durumlarda, çevreyle olan etkileşimlerden yaklaşık olarak tahmin edebiliriz - veya "öğrenebiliriz". Bu, adındaki "$Q$-öğrenme" kısmıdır. İçinde "derin" kelimesi de var çünkü bu fonksiyona yaklaşmak için evrensel fonksiyon tahmin edicileri olan derin sinir ağlarını kullanacağız. Yaklaşık $Q$ değerlerine yaklaşan derin sinir ağları, Derin Q-Ağları (DQN) olarak adlandırıldı. Basit ortamlarda (belleğe uyan durumların sayısı ile), $Q$-işlevini temsil etmek için sinir ağı yerine sadece bir tablo kullanılabilir, bu durumda buna “tabular $Q$-öğrenme” adı verilir.

Dolayısıyla şimdiki amacımız $Q^*$ fonksiyonunu yaklaşık olarak bulmaktır. Bellman denklemini kullanacağız:

\[Q(s, a) = r + γ \space \textrm{maks}_{a'} Q(s', a')\]

$s'$, $s$'dan sonraki durumdur. $γ$ (gama), tipik olarak 0,99, bir indirim faktörüdür (bir hiper parametredir). Gelecekteki ödüllere daha az ağırlık verir (çünkü kusurlu $Q$ ile anlık ödüllerden daha az kesindirler). Bellman denklemi, derin $Q$-öğrenmenin merkezinde yer alır. Belirli bir durum ve eylem için $Q$-değerinin, $a$ eylemi yapıldıktan sonra alınan bir $r$ ödülü artı $s'$'a indiğimiz durum için en yüksek $Q$-değeri olduğunu söylüyor. En yüksek değer, bir anlamda $a'$ eylemini seçmemizdir, bu da $s'$'dan en yüksek toplam getiriye yol açar.

Bellman denklemiyle, $Q^*$'a yaklaşmak için denetimli öğrenmeyi kullanabiliriz. $Q$-işlevi, $θ$ (teta) olarak gösterilen sinir ağı ağırlıkları ile temsil edilecektir (parametrelendirilecektir). Basit bir uygulama, ağ girişi olarak bir durum ve bir eylem alır ve Q-değerini çıkarır. Verimsizlik, belirli bir durumdaki tüm eylemler için $Q$-değerlerini bilmek istiyorsak, eylemler olduğu kadar çok kez $Q$ çağırmamız gerektiğidir. Çok daha iyi bir yol var: yalnızca durumu girdi olarak almak ve olası tüm eylemler için $Q$-değerlerini çıkarmak. Bu sayede, sadece bir ileri geçişte tüm eylemler için $Q$-değerleri elde edebiliriz.

$Q$ ağını rastgele ağırlıklarla eğitmeye başlıyoruz. Çevreden birçok geçiş (veya “deneyim”) elde ederiz. Bunlar (durum, eylem, sonraki durum, ödül) veya kısaca ($s$, $a$, $s'$, $r$) demetleridir. Binlercesini "deneyim tekrarı" adı verilen bir halka arabelleğinde saklarız. Ardından, Bellman denkleminin onlar için tutması arzusuyla bu tampondaki deneyimleri örnekliyoruz. Arabelleği atlayabilir ve deneyimleri tek tek uygulayabilirdik (buna “çevrimiçi” veya “politika üzerine” denir); sorun, sonraki deneyimlerin birbiriyle yüksek oranda ilişkili olması ve bu gerçekleştiğinde DQN'nin zayıf çalışmasıdır. Bu nedenle, bu veri korelasyonunu kırmak için deneyim tekrarı ("çevrimdışı", "politika dışı" bir yaklaşım) tanıtıldı. En basit halka arabelleği uygulamamızın kodu replay_buffer.py dosyasında bulunabilir, okumanızı tavsiye ederim.

Başlangıçta, sinir ağı ağırlıklarımız rastgele olduğundan, Bellman denkleminin sol taraftaki değeri sağ taraftan uzak olacaktır. Kare farkı kayıp fonksiyonumuz olacaktır. Sinir ağı ağırlıklarını $θ$ değiştirerek kayıp fonksiyonunu en aza indireceğiz. Kayıp fonksiyonumuzu yazalım:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{maks}_{a'}Q(s', a')]^2\]

Bu yeniden yazılmış bir Bellman denklemi. Dağ Arabası deneyim tekrarından bir deneyim ($s$, sol, $s'$, -1) örneklediğimizi varsayalım. $s$ durumuyla $Q$ ağımız üzerinden ileriye doğru bir geçiş yapıyoruz ve örneğin kalan işlem için bize -120 veriyor. Yani, $Q(s, \textrm{sol}) = -120$. Sonra ağa $s'$ besleriz, bu da bize örneğin sol için -130 ve sağ için -122 verir. Yani açıkça $s'$ için en iyi eylem doğrudur, dolayısıyla $\textrm{max}_{a'}Q(s', a') = -122$. $r$ biliyoruz, bu gerçek ödül, -1 idi. Dolayısıyla $Q$-network tahminimiz biraz yanlıştı çünkü $L(θ) = [-120 - 1 + 0.99 ⋅ 122]^2 = (-0.22^2) = 0.0484$. Bu yüzden hatayı geriye doğru yayar ve $θ$ ağırlıklarını biraz düzeltiriz. Aynı deneyim için kaybı tekrar hesaplayacak olsaydık, şimdi daha düşük olurdu.

Kodlamaya geçmeden önce önemli bir gözlem. DQN'mizi güncellemek için DQN'nin kendisinde iki ileri geçiş yapacağımıza dikkat edelim. Bu genellikle kararsız öğrenmeye yol açar. Bunu hafifletmek için, bir sonraki durum $Q$ tahmini için aynı DQN'yi kullanmıyoruz. Bunun kodda target_model olarak adlandırılan daha eski bir sürümünü kullanıyoruz (ana DQN olan model yerine). Bu sayede istikrarlı bir hedefimiz var. Her 1000 adımda bir model ağırlıklarına ayarlayarak target_model güncelleriz. Ancak model her adımda güncellenir.

DQN modelini oluşturan koda bakalım:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

İlk olarak, işlev, verilen OpenAI Gym ortamından eylem ve gözlem alanı boyutlarını alır. Örneğin ağımızın kaç çıktıya sahip olacağını bilmek gerekir. Eylem sayısına eşit olmalıdır. Eylemler bir sıcak kodlanmıştır:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Yani (örn.) sol [1, 0] ve sağ [0, 1] olacaktır.

Gözlemlerin girdi olarak aktarıldığını görebiliriz. Ayrıca action_mask ikinci girdi olarak geçiyoruz. Niye ya? $Q(s,a)$'ı hesaplarken, verilen eylemin tümü için değil, yalnızca bir eylem için $Q$-değerini bilmemiz gerekir. action_mask , DQN çıktısına iletmek istediğimiz eylemler için 1 içerir. action_mask bazı eylemler için 0 varsa, çıktıda karşılık gelen $Q$-değeri sıfırlanır. filtered_output katmanı bunu yapıyor. Tüm $Q$-değerlerini istiyorsak (maksimum hesaplama için), hepsini geçebiliriz.

Kod, tamamen bağlı bir katmanı tanımlamak için keras.layers.Dense kullanır. Keras, TensorFlow'un üstünde daha üst düzey soyutlama için bir Python kitaplığıdır. Kaputun altında Keras, önyargılar, uygun ağırlık başlatma ve diğer düşük seviyeli şeyler içeren bir TensorFlow grafiği oluşturur. Grafiği tanımlamak için ham TensorFlow'u kullanabilirdik, ancak bu tek satırlı olmayacak.

Böylece gözlemler, ReLU (düzeltilmiş doğrusal birim) aktivasyonları ile ilk gizli katmana iletilir. ReLU(x) yalnızca bir $\textrm{max}(0, x)$ işlevidir. Bu katman, ikinci bir özdeş katmanla tamamen bağlantılıdır, hidden_2 . Çıkış katmanı, nöron sayısını eylem sayısına indirger. Sonunda, çıktıyı action_mask ile çarpan filtered_output var.

$θ$ ağırlıklarını bulmak için, ortalama kare hata kaybı olan “Adam” adlı bir optimize edici kullanacağız.

Bir modele sahip olarak, verilen durum gözlemleri için $Q$ değerlerini tahmin etmek için kullanabiliriz:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Tüm eylemler için $Q$-değerleri istiyoruz, bu nedenle action_mask bir birlerin vektörüdür.

Asıl eğitimi yapmak için fit_batch() kullanacağız:

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Toplu iş, BATCH_SIZE deneyim içeriyor. next_q_values ​​$Q(s, a)$'dır. q_values , Bellman denkleminden $r + γ \space \textrm{max}_{a'}Q(s', a')$'dır. Yaptığımız eylemler bir sıcak kodlanmış ve model.fit() girişe action_mask olarak geçirildi. $y$, denetimli öğrenmede bir "hedef" için ortak bir harftir. Burada q_values . q_values[:. None] yapıyorum. q_values[:. None] , one_hot_actions dizisinin boyutuna karşılık gelmesi gerektiğinden dizi boyutunu artırmak için. Bununla ilgili daha fazlasını okumak isterseniz buna dilim notasyonu denir.

Kaybı TensorBoard günlük dosyasına kaydetmek ve daha sonra görselleştirmek için iade ediyoruz. İzleyeceğimiz daha bir çok şey var: saniyede kaç adım atıyoruz, toplam RAM kullanımı, ortalama bölüm dönüşü ne kadar, vs. O grafiklere bir bakalım.

Koşma

TensorBoard günlük dosyasını görselleştirmek için önce bir taneye ihtiyacımız var. Öyleyse eğitimi çalıştıralım:

 python run.py

Bu ilk önce modelimizin özetini yazdıracaktır. Ardından güncel tarih ile bir günlük dizini oluşturacak ve eğitime başlayacaktır. Her 2000 adımda bir, şuna benzer bir günlük satırı yazdırılacaktır:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Her 20.000'de bir, modelimizi 10.000 adımda değerlendireceğiz:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

677 bölüm ve 120.000 adımdan sonra, ortalama bölüm dönüşü -200'den -136.75'e yükseldi! Kesinlikle öğreniyor. avg_max_q_value nedir, okuyucuya iyi bir alıştırma olarak bırakıyorum. Ancak eğitim sırasında bakmak için çok yararlı bir istatistik.

200.000 adımdan sonra eğitimimiz tamamlanmıştır. Dört çekirdekli CPU'mda yaklaşık 20 dakika sürüyor. date-log dizininin içine bakabiliriz, örneğin, 06-07-18-39-log . .h5 uzantılı dört model dosyası olacaktır. Bu, TensorFlow grafik ağırlıklarının bir anlık görüntüsüdür, daha sonra öğrendiğimiz politikaya bir göz atmak için her 50.000 adımda bir onları kaydederiz. Görüntülemek için:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Diğer olası bayrakları görmek için: python run.py --help .

Artık araba, istenen hedefe ulaşmak için çok daha iyi bir iş çıkarıyor. date-log dizininde ayrıca events.out.* dosyası da vardır. Bu, TensorBoard'un verilerini depoladığı dosyadır. loggers.py içinde tanımlanan en basit TensorBoardLogger kullanarak ona loggers.py. Olaylar dosyasını görüntülemek için yerel TensorBoard sunucusunu çalıştırmamız gerekiyor:

 tensorboard --logdir=.

--logdir sadece tarih-günlük dizinlerinin bulunduğu dizine işaret eder, bizim durumumuzda bu geçerli dizin olacaktır, yani . . TensorBoard, dinlediği URL'yi yazdırır. http://127.0.0.1:6006 sayfasını açarsanız, şunlara benzer sekiz grafik görmelisiniz:

Toplama

train() tüm eğitimi yapar. İlk önce modeli oluşturuyoruz ve tamponu tekrar oynatıyoruz. Ardından, see.py çok benzer bir döngüde, çevre ile etkileşime girer ve deneyimleri arabellekte saklarız. Önemli olan epsilon açgözlü bir politika izlememizdir. $Q$ işlevine göre her zaman en iyi eylemi seçebiliriz; ancak bu, genel performansa zarar veren araştırmayı caydırır. Bu nedenle, epsilon olasılığıyla araştırmayı zorlamak için rastgele eylemler gerçekleştiririz:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon %1 olarak ayarlandı. 2000 deneyimden sonra tekrar, eğitime başlamak için yeterince doluyor. Bunu, tekrar arabelleğinden örneklenen rastgele bir deneyim fit_batch() çağırarak yaparız:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Her 20.000 adımda bir sonuçları değerlendirir ve günlüğe kaydederiz (değerlendirme epsilon = 0 ile yapılır, tamamen açgözlü politika):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

Kodun tamamı yaklaşık 300 satırdır ve run.py en önemlilerinden yaklaşık 250 tanesini içerir.

Bir çok hiperparametre olduğunu fark edebilirsiniz:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Ve bu bile hepsi değil. Ayrıca bir ağ mimarisi var; 32 nöronlu iki gizli katman, ReLU aktivasyonları ve Adam optimizer kullandık, ancak birçok başka seçenek var. Küçük değişiklikler bile eğitim üzerinde büyük bir etkiye sahip olabilir. Hiperparametreleri ayarlamak için çok zaman harcanabilir. Yakın tarihli bir OpenAI yarışmasında, ikinci olan bir yarışmacı, hiperparametre ayarından sonra Rainbow'un puanını neredeyse ikiye katlamanın mümkün olduğunu keşfetti. Doğal olarak, fazla takmanın kolay olduğunu unutmamak gerekir. Şu anda, güçlendirme algoritmaları, benzer ortamlara bilgi aktarımı ile mücadele ediyor. Dağ Arabamız şu anda her türlü dağa genelleme yapmıyor. OpenAI Gym ortamını gerçekten değiştirebilir ve aracının ne kadar genelleştirebileceğini görebilirsiniz.

Başka bir alıştırma benimkinden daha iyi bir hiperparametre seti bulmak olacak. Kesinlikle mümkün. Ancak, değişikliğinizin bir gelişme olup olmadığına karar vermek için tek bir antrenman çalışması yeterli olmayacaktır. Antrenman koşuları arasında genellikle büyük bir fark vardır; fark büyüktür. Bir şeyin daha iyi olduğunu belirlemek için birçok koşuya ihtiyacınız olacak. Tekrarlanabilirlik gibi önemli bir konu hakkında daha fazla bilgi edinmek istiyorsanız, Derin Takviyeli Öğrenmenin Önemli Olması'nı okumanızı tavsiye ederim. Elle ayarlamak yerine, soruna daha fazla bilgi işlem gücü harcamaya istekliysek, bu süreci bir dereceye kadar otomatikleştirebiliriz. Basit bir yaklaşım, bazı hiperparametreler için umut verici bir değer aralığı hazırlamak ve daha sonra paralel olarak çalışan eğitimlerle bir ızgara araması (kombinasyonlarını kontrol ederek) yapmaktır. Paralelleştirme, yüksek performans için çok önemli olduğu için başlı başına büyük bir konudur.

Derin $Q$-öğrenme, değer yinelemesini kullanan büyük bir pekiştirmeli öğrenme algoritmaları ailesini temsil eder. $Q$-fonksiyonuna yaklaşmaya çalıştık ve onu çoğu zaman açgözlü bir şekilde kullandık. İlke yinelemesini kullanan başka bir aile var. $Q$-fonksiyonuna yaklaşmaya değil, doğrudan $π^*$ optimal politikasını bulmaya odaklanırlar. Takviyeli öğrenme algoritmaları ortamında değer yinelemesinin nereye uyduğunu görmek için:

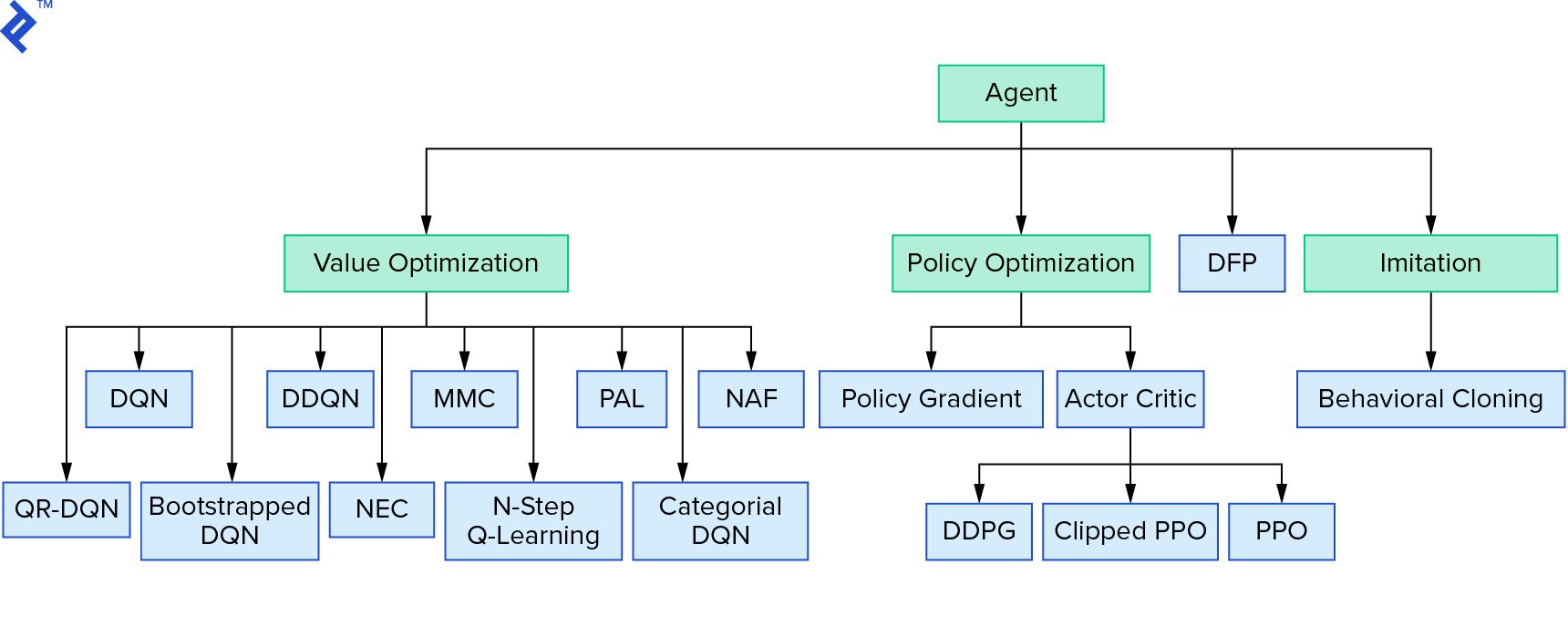
Düşünceleriniz, derin pekiştirmeli öğrenmenin kırılgan göründüğü olabilir. haklı çıkacaksın; birçok sorun var. Derin Takviyeli Öğrenme Henüz Çalışmıyor ve Takviyeli Öğrenme hiçbir zaman işe yaramadı ve 'derin' sadece biraz yardımcı oldu.

Bu, öğreticiyi tamamlar. Öğrenme amacıyla kendi temel DQN'mizi uyguladık. Bazı Atari oyunlarında iyi performans elde etmek için çok benzer kodlar kullanılabilir. Pratik uygulamalarda, genellikle test edilmiş, yüksek performanslı uygulamalar, örneğin OpenAI taban çizgilerinden biri alınır. Daha karmaşık bir ortamda derin pekiştirmeli öğrenmeyi uygulamaya çalışırken karşılaşabileceğiniz zorlukları görmek isterseniz, NIPS 2017: Çalıştırmayı Öğrenme yaklaşımımızı okuyabilirsiniz. Eğlenceli bir yarışma ortamında daha fazlasını öğrenmek istiyorsanız NIPS 2018 Competitions veya crowdai.org'a göz atın.

Bir makine öğrenimi uzmanı olma yolundaysanız ve denetimli öğrenme konusundaki bilginizi derinleştirmek istiyorsanız, balıkları tanımlamaya yönelik eğlenceli bir deney için Makine Öğrenimi Video Analizi: Balıkları Tanımlama'ya göz atın.