الغوص العميق في التعلم المعزز

دعونا نلقي نظرة عميقة على التعلم المعزز. في هذه المقالة ، سوف نتعامل مع مشكلة ملموسة مع المكتبات الحديثة مثل TensorFlow و TensorBoard و Keras و OpenAI gym. سترى كيفية تنفيذ إحدى الخوارزميات الأساسية المسماة deep $ Q $ -learning لتتعلم طريقة عملها الداخلية. فيما يتعلق بالأجهزة ، سيعمل الكود بالكامل على جهاز كمبيوتر نموذجي ويستخدم جميع نوى وحدة المعالجة المركزية (يتم التعامل مع هذا خارج الصندوق بواسطة TensorFlow).

المشكلة تسمى Mountain Car: السيارة تسير على مسار أحادي البعد ، بين جبلين. الهدف هو قيادة الجبل على اليمين (الوصول إلى العلم). ومع ذلك ، فإن محرك السيارة ليس بالقوة الكافية لتسلق الجبل في ممر واحد. لذلك ، فإن الطريقة الوحيدة للنجاح هي القيادة ذهابًا وإيابًا لبناء الزخم.

تم اختيار هذه المشكلة لأنها بسيطة بما يكفي لإيجاد حل مع التعلم المعزز في دقائق على نواة واحدة لوحدة المعالجة المركزية. ومع ذلك ، فهي معقدة بما يكفي لتكون ممثلًا جيدًا.

أولاً ، سأقدم ملخصًا موجزًا ​​لما يفعله التعلم المعزز بشكل عام. ثم سنغطي المصطلحات الأساسية ونعبر عن مشكلتنا معهم. بعد ذلك ، سوف أصف خوارزمية التعلم العميق $ Q $ وسنقوم بتنفيذها لحل المشكلة.

أساسيات التعلم المعزز

التعلم المعزز بأبسط الكلمات هو التعلم عن طريق التجربة والخطأ. الشخصية الرئيسية تسمى "الوكيل" ، والتي ستكون سيارة في مشكلتنا. يقوم الوكيل بعمل ما في بيئة ما ويتم إعطاؤه ملاحظة جديدة ومكافأة لهذا الإجراء. يتم تعزيز الإجراءات التي تؤدي إلى مكافآت أكبر ، ومن هنا جاءت التسمية. كما هو الحال مع العديد من الأشياء الأخرى في علوم الكمبيوتر ، كان هذا أيضًا مستوحى من مراقبة الكائنات الحية.

يتم تلخيص تفاعلات الوكيل مع البيئة في الرسم البياني التالي:

يحصل الوكيل على ملاحظة ومكافأة للعمل المنجز. ثم يقوم بعمل آخر ويأخذ الخطوة الثانية. تعيد البيئة الآن (على الأرجح) ملاحظة ومكافأة مختلفة قليلاً. يستمر هذا حتى يتم الوصول إلى الحالة النهائية ، والتي يتم الإشارة إليها عن طريق إرسال "تم" إلى وكيل. يُطلق على التسلسل الكامل للملاحظات> الإجراءات> الملاحظات التالية> المكافآت حلقة (أو مسار).

العودة إلى سيارتنا الجبلية: سيارتنا وكيل. البيئة هي عالم الصندوق الأسود للجبال أحادية البعد. يتلخص عمل السيارة في رقم واحد فقط: إذا كان موجبًا ، يدفع المحرك السيارة إلى اليمين. إذا كانت سلبية ، فإنها تدفع السيارة إلى اليسار. يدرك الوكيل بيئة من خلال ملاحظة: موضع السيارة X وسرعتها. إذا أردنا أن تسير سيارتنا على قمة الجبل ، فإننا نحدد المكافأة بطريقة مناسبة: يحصل الوكيل على -1 من مكافأته عن كل خطوة لم تصل فيها إلى الهدف. عندما تصل إلى الهدف تنتهي الحلقة. لذلك ، في الواقع ، يعاقب الوكيل لأنه لم يكن في وضع نريده أن يكون. كلما وصل إليه أسرع ، كان ذلك أفضل بالنسبة له. هدف الوكيل هو زيادة إجمالي المكافأة إلى الحد الأقصى ، وهو مجموع المكافآت من حلقة واحدة. لذلك إذا وصلت إلى النقطة المرغوبة بعد ، على سبيل المثال ، 110 خطوة ، فإنها تتلقى عائدًا إجماليًا قدره -110 ، والتي ستكون نتيجة رائعة لـ Mountain Car ، لأنها إذا لم تصل إلى الهدف ، فستتم معاقبتها على 200 خطوة (وبالتالي ، عودة -200).

هذه هي صياغة المشكلة برمتها. الآن ، يمكننا أن نعطيها للخوارزميات ، والتي هي بالفعل قوية بما يكفي لحل مثل هذه المشاكل في غضون دقائق (إذا تم ضبطها جيدًا). تجدر الإشارة إلى أننا لا نخبر الوكيل بكيفية تحقيق الهدف. نحن لا نقدم حتى أي تلميحات (الاستدلال). سيجد الوكيل طريقة (سياسة) للفوز بمفرده.

تهيئة البيئة

أولاً ، انسخ كود البرنامج التعليمي بالكامل على القرص الخاص بك:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

الآن ، نحتاج إلى تثبيت حزم Python التي سنستخدمها. لعدم تثبيتها في مساحة المستخدمين الخاصة بك (والتصادمات الخطرة) ، سنقوم بتنظيفها وتثبيتها في بيئة conda. إذا لم يكن لديك conda مثبتًا ، فيرجى اتباع https://conda.io/docs/user-guide/install/index.html.

لإنشاء بيئة كوندا لدينا:

 conda create -n tutorial python=3.6.5 -y

لتفعيلها:

 source activate tutorial

يجب أن ترى (tutorial) بالقرب من موجهك في shell. هذا يعني أن بيئة كوندا مع اسم "تعليمي" نشطة. من الآن فصاعدًا ، يجب تنفيذ جميع الأوامر داخل بيئة كوندا.

الآن ، يمكننا تثبيت جميع التبعيات في بيئة كوندا محكمة الغلق الخاصة بنا:

 pip install -r requirements.txt

لقد انتهينا من التثبيت ، لذا فلنقم بتشغيل بعض التعليمات البرمجية. لسنا بحاجة إلى تطبيق بيئة Mountain Car بأنفسنا ؛ توفر مكتبة OpenAI Gym هذا التنفيذ. دعنا نرى عاملًا عشوائيًا (وكيل يتخذ إجراءات عشوائية) في بيئتنا:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

هذا ملف see.py ؛ لتشغيله ، قم بتنفيذ:

 python see.py

يجب أن ترى سيارة تسير بشكل عشوائي ذهابًا وإيابًا. ستتألف كل حلقة من 200 خطوة ؛ العائد الإجمالي سيكون -200.

الآن نحن بحاجة إلى استبدال الإجراءات العشوائية بشيء أفضل. هناك العديد من الخوارزميات التي يمكن للمرء استخدامها. بالنسبة لبرنامج تعليمي تمهيدي ، أعتقد أن أسلوبًا يسمى التعلم العميق $ Q $ -ليترنج مناسبًا جيدًا. إن فهم هذه الطريقة يعطي أساسًا ثابتًا لتعلم الأساليب الأخرى.

التعلم العميق بالدولار القطري بالدولار الأمريكي

تم وصف الخوارزمية التي سنستخدمها لأول مرة في عام 2013 بواسطة Mnih et al. في لعب أتاري مع التعلم المعزز العميق وصقله بعد ذلك بعامين في التحكم على مستوى الإنسان من خلال التعلم المعزز العميق. تم بناء العديد من الأعمال الأخرى على تلك النتائج ، بما في ذلك خوارزمية قوس قزح الحديثة (2017):

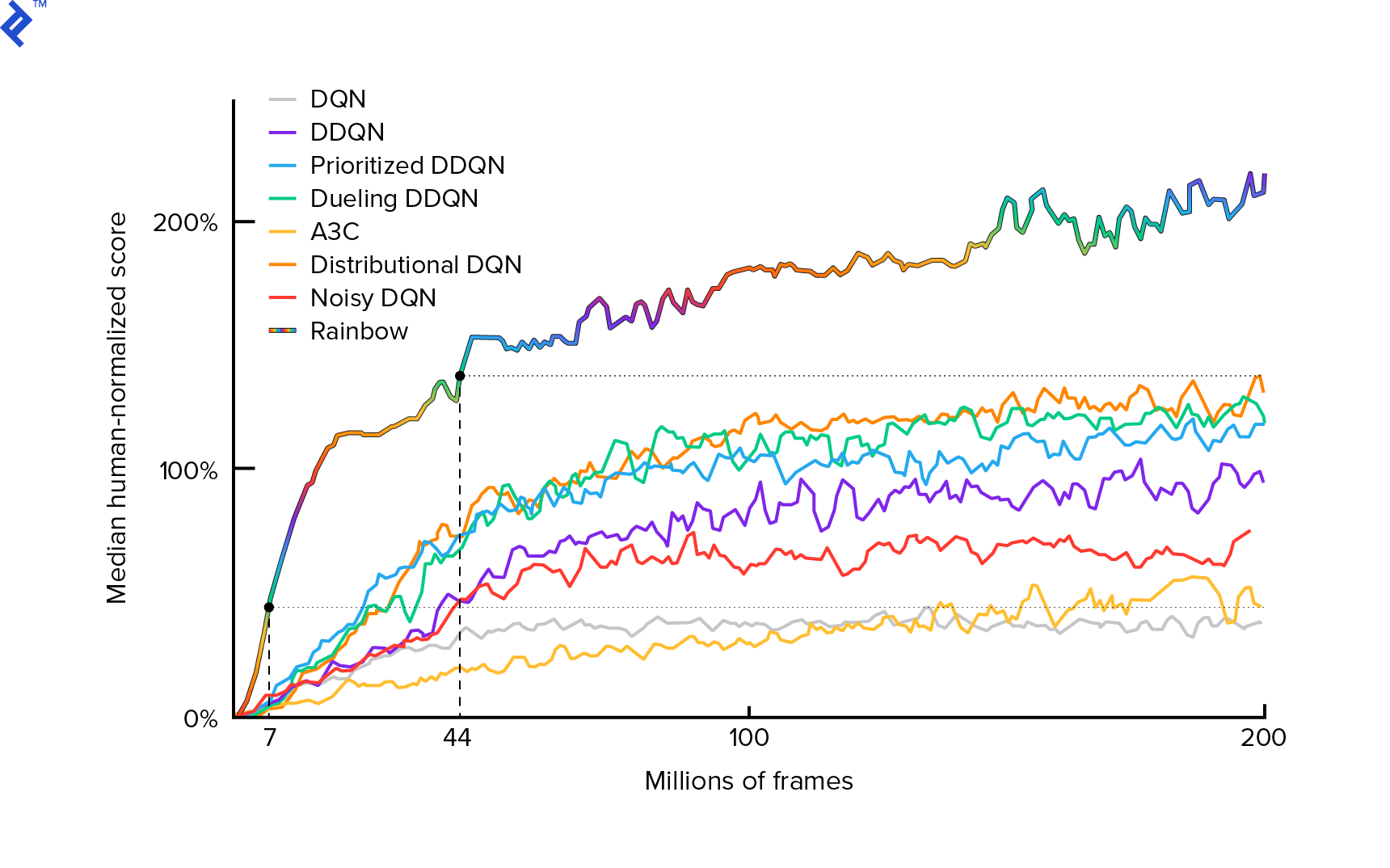
يحقق قوس قزح أداءً خارقًا في العديد من ألعاب أتاري 2600. سنركز على إصدار DQN الأساسي ، مع أصغر عدد ممكن من التحسينات الإضافية ، للحفاظ على هذا البرنامج التعليمي بحجم معقول.

السياسة ، التي يُشار إليها عادةً $ π (s) $ ، هي دالة تعرض احتمالات اتخاذ إجراءات فردية في حالة معينة $ s $. لذلك ، على سبيل المثال ، تُرجع سياسة Mountain Car العشوائية لأي ولاية: 50٪ يسار ، 50٪ يمين. أثناء اللعب ، نقوم بأخذ عينات من تلك السياسة (التوزيع) للحصول على إجراءات حقيقية.

يشير $ Q $ -learning (Q is for Quality) إلى دالة قيمة الإجراء المشار إليها $ Q_π (s، a) $. تقوم بإرجاع إجمالي العائد من حالة معينة $ s $ ، واختيار الإجراء $ a $ ، باتباع سياسة محددة $ π $. العائد الإجمالي هو مجموع كل المكافآت في حلقة واحدة (المسار).

إذا عرفنا الوظيفة المثالية $ Q $ ، والمشار إليها $ Q ^ * $ ، يمكننا حل اللعبة بسهولة. سنتبع الإجراءات ذات القيمة الأعلى $ Q ^ * $ ، أي أعلى عائد متوقع. هذا يضمن أننا سنصل إلى أعلى عائد ممكن.

ومع ذلك ، فإننا غالبًا لا نعرف $ Q ^ * $. في مثل هذه الحالات ، يمكننا تقريب - أو "التعلم" - من التفاعلات مع البيئة. هذا هو جزء “$ Q $ -learning” في الاسم. هناك أيضًا كلمة "عميق" فيها لأنه ، لتقريب هذه الوظيفة ، سنستخدم الشبكات العصبية العميقة ، والتي تعد مقاربًا للوظائف العالمية. تم تسمية الشبكات العصبية العميقة التي تقارب قيم $ Q $ - Deep Q-Networks (DQN). في البيئات البسيطة (مع عدد الحالات المناسبة في الذاكرة) ، يمكن للمرء فقط استخدام جدول بدلاً من الشبكة العصبية لتمثيل وظيفة $ Q $ ، وفي هذه الحالة سيتم تسميتها "tabular $ Q $ -learning".

لذا فإن هدفنا الآن هو تقريب الدالة $ Q ^ * $. سنستخدم معادلة بيلمان:

\ [Q (s، a) = r + γ \ space \ textrm {max} _ {a '} Q (s'، a ') \]

$ s '$ هي الولاية بعد $ s $. $ γ $ (جاما) ، عادةً 0.99 ، هو عامل خصم (إنه معلمة فائقة). إنها تضع وزنًا أقل على المكافآت المستقبلية (لأنها أقل يقينًا من المكافآت الفورية مع عدم اكتمال قيمة المكافآت التي نحصل عليها من دولارات الولايات المتحدة). تعتبر معادلة بيلمان أساسية للتعلم العميق بالدولار القطري بالدولار الأمريكي. تقول أن قيمة $ Q $ لحالة معينة وإجراء هو مكافأة $ r $ تم استلامها بعد اتخاذ الإجراء $ a $ بالإضافة إلى أعلى قيمة $ Q $ للحالة التي نصل إليها $ s '$. أعلى قيمة بمعنى أننا نختار الإجراء $ a '$ ، والذي يؤدي إلى أعلى إجمالي عائد من $ s' $.

باستخدام معادلة بيلمان ، يمكننا استخدام التعلم الخاضع للإشراف لتقريب $ Q ^ * $. سيتم تمثيل الدالة $ Q $ (معلمات) بواسطة أوزان الشبكة العصبية المشار إليها بـ $ θ $ (ثيتا). سيتخذ التنفيذ المباشر حالة وإجراء كمدخل للشبكة وإخراج قيمة Q. عدم الكفاءة هو أننا إذا أردنا معرفة قيم $ Q $ لجميع الإجراءات في حالة معينة ، فنحن بحاجة إلى استدعاء $ Q $ عدة مرات مثل الإجراءات. هناك طريقة أفضل بكثير: أخذ الحالة فقط كمدخلات ومخرجات $ Q $ -values ​​لجميع الإجراءات الممكنة. بفضل ذلك ، يمكننا الحصول على قيم $ Q $ -values ​​لجميع الإجراءات في تمريرة أمامية واحدة فقط.

نبدأ في تدريب شبكة $ Q $ باستخدام أوزان عشوائية. من البيئة ، نحصل على العديد من التحولات (أو "الخبرات"). هذه هي مجموعات (الحالة ، الإجراء ، الحالة التالية ، المكافأة) أو باختصار ($ s $ ، $ a $ ، $ s '$ ، $ r $). نقوم بتخزين الآلاف منها في مخزن مؤقت يسمى "إعادة تشغيل التجربة". بعد ذلك ، نقوم بأخذ عينات من التجارب من هذا المخزن المؤقت مع الرغبة في أن تحمل معادلة بيلمان لهم. كان بإمكاننا تخطي المخزن المؤقت وتطبيق الخبرات واحدًا تلو الآخر (وهذا ما يسمى "عبر الإنترنت" أو "على السياسة") ؛ تكمن المشكلة في أن التجارب اللاحقة ترتبط ارتباطًا وثيقًا ببعضها البعض وقطارات DQN سيئة عند حدوث ذلك. لهذا السبب تم تقديم تجربة إعادة التشغيل (نهج "غير متصل" و "خارج السياسة") لكسر ارتباط البيانات هذا. يمكن العثور على الكود الخاص بأبسط تطبيق للمخزن المؤقت الحلقي لدينا في ملف replay_buffer.py ، وأنا أشجعك على قراءته.

في البداية ، نظرًا لأن أوزان شبكتنا العصبية كانت عشوائية ، فإن قيمة الجانب الأيسر لمعادلة بيلمان ستكون بعيدة عن الجانب الأيمن. سيكون الفرق التربيعي هو دالة الخسارة. سنقلل من وظيفة الخسارة عن طريق تغيير أوزان الشبكة العصبية $ θ $. دعنا نكتب دالة الخسارة لدينا:

\ [L (θ) = [Q (s، a) - r - γ \ space \ textrm {max} _ {a '} Q (s'، a ')] ^ 2 \]

إنها معادلة بيلمان مُعاد كتابتها. لنفترض أننا أخذنا عينة من تجربة ($ s $ ، left ، $ s '$ ، -1) من إعادة تشغيل تجربة Mountain Car. نقوم بتمرير أمامي عبر شبكة $ Q $ الخاصة بنا مع الحالة $ s $ وللإجراء المتبقي ، نحصل على -120 ، على سبيل المثال. إذن ، $ Q (s، \ textrm {left}) = -120 $. ثم نقوم بتغذية $ s '$ للشبكة ، مما يعطينا ، على سبيل المثال ، -130 لليسار و -122 لليمين. من الواضح أن أفضل إجراء لـ $ s '$ هو الصحيح ، وبالتالي فإن $ \ textrm {max} _ {a'} Q (s '، a') = -122 $. نعلم $ r $ ، هذه هي المكافأة الحقيقية ، والتي كانت -1. لذلك كان توقعنا على الشبكة $ Q $ خاطئًا بعض الشيء ، لأن $ L (θ) = [-120 - 1 + 0.99 ⋅ 122] ^ 2 = (-0.22 ^ 2) = 0.0484 $. لذا فإننا نعيد نشر الخطأ إلى الوراء ونصحح الأوزان $ θ $ قليلاً. إذا قمنا بحساب الخسارة مرة أخرى لنفس التجربة ، فستكون الآن أقل.

ملاحظة مهمة قبل أن نذهب إلى الكود. دعنا نلاحظ أنه لتحديث DQN الخاص بنا ، سنقوم بتمريرتين للأمام على DQN… نفسه. هذا غالبا ما يؤدي إلى تعلم غير مستقر. للتخفيف من ذلك ، بالنسبة للتنبؤ التالي بالدولار الأمريكي Q $ ، فإننا لا نستخدم نفس DQN. نستخدم إصدارًا أقدم منه ، والذي يسمى في الكود target_model (بدلاً من model ، كونه DQN الرئيسي). بفضل ذلك ، لدينا هدف مستقر. نقوم بتحديث target_model من خلال ضبطه على أوزان model كل 1000 خطوة. لكن model يقوم بتحديث كل خطوة.

لنلقِ نظرة على الكود الذي ينشئ نموذج DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

أولاً ، تأخذ الوظيفة أبعاد مساحة العمل والمراقبة من بيئة OpenAI Gym المحددة. من الضروري معرفة ، على سبيل المثال ، عدد النواتج التي ستحصل عليها شبكتنا. يجب أن تكون مساوية لعدد الإجراءات. الإجراءات هي واحدة مشفرة ساخنة:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

لذلك (على سبيل المثال) اليسار سيكون [1 ، 0] واليمين سيكون [0 ، 1].

يمكننا أن نرى الملاحظات يتم تمريرها كمدخلات. نمرر أيضًا action_mask كمدخل ثانٍ. لماذا ا؟ عند حساب $ Q (s، a) $ ، نحتاج إلى معرفة قيمة $ Q $ -value فقط لإجراء معين واحد ، وليس جميعها. يحتوي action_mask على 1 للإجراءات التي نريد تمريرها إلى إخراج DQN. إذا كانت action_mask تحتوي على 0 لبعض الإجراءات ، فسيتم عندئذٍ تساقط القيمة المطابقة $ Q $ -value على الناتج. تقوم طبقة filtered_output بذلك. إذا أردنا جميع قيم $ Q $ (للحساب الأقصى) ، يمكننا فقط تمرير كل القيم.

يستخدم الكود keras.layers.Dense لتعريف طبقة متصلة بالكامل. Keras هي مكتبة Python للتجريد عالي المستوى أعلى TensorFlow. تحت غطاء المحرك ، ينشئ Keras رسمًا بيانيًا TensorFlow ، مع وجود تحيزات وتهيئة مناسبة للوزن وأشياء أخرى منخفضة المستوى. كان بإمكاننا فقط استخدام TensorFlow الخام لتحديد الرسم البياني ، لكنه لن يكون سطرًا واحدًا.

لذلك يتم تمرير الملاحظات إلى الطبقة المخفية الأولى ، مع تنشيط ReLU (الوحدة الخطية المصححة). ReLU(x) هي مجرد دالة $ \ textrm {max} (0، x) $. هذه الطبقة متصلة تمامًا بطبقة ثانية متطابقة ، hidden_2 . تقوم طبقة الإخراج بإسقاط عدد الخلايا العصبية إلى عدد الإجراءات. في النهاية ، لدينا filtered_output ، والذي يضاعف الناتج باستخدام action_mask .

للعثور على أوزان $ θ $ ، سنستخدم مُحسِّنًا اسمه "Adam" بمتوسط ​​خسارة خطأ في التربيعية.

بوجود نموذج ، يمكننا استخدامه للتنبؤ بقيم $ Q $ لملاحظات الحالة المعينة:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

نريد قيمًا بقيمة $ Q $ لكل الإجراءات ، وبالتالي فإن action_mask هو متجه لتلك الإجراءات.

للقيام بالتدريب الفعلي ، سنستخدم fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

تحتوي المجموعة على BATCH_SIZE تجربة. next_q_values ​​هو $ Q (s، a) $. q_values ​​هي $ r + γ \ space \ textrm {max} _ {a '} Q (s'، a ') $ من معادلة بيلمان. الإجراءات التي اتخذناها هي واحدة مشفرة ساخنة وتم تمريرها كـ action_mask إلى الإدخال عند استدعاء model.fit() . $ y $ هو حرف شائع لـ "الهدف" في التعلم الخاضع للإشراف. نحن هنا نمرر q_values . أفعل q_values[:. None] q_values[:. None] لزيادة أبعاد المصفوفة لأنه يجب أن يتوافق مع أبعاد مصفوفة one_hot_actions . وهذا ما يسمى بالتدوين المقطعي إذا كنت ترغب في قراءة المزيد عنها.

نعيد الخسارة لحفظها في ملف سجل TensorBoard ثم تصورها لاحقًا. هناك العديد من الأشياء الأخرى التي سنراقبها: كم عدد الخطوات في الثانية التي نقوم بها ، إجمالي استخدام ذاكرة الوصول العشوائي ، ما هو متوسط ​​عودة الحلقة ، وما إلى ذلك. دعنا نرى هذه المؤامرات.

ادارة

لتصور ملف سجل TensorBoard ، نحتاج أولاً إلى امتلاك واحد. لذلك دعونا ندير التدريب:

 python run.py

سيؤدي هذا أولاً إلى طباعة ملخص نموذجنا. ثم يقوم بإنشاء دليل سجل بالتاريخ الحالي ويبدأ التدريب. كل 2000 خطوة ، ستتم طباعة سطر تسجيل مشابه لما يلي:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

كل 20000 ، سنقوم بتقييم نموذجنا على 10000 خطوة:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

بعد 677 حلقة و 120.000 خطوة ، تحسن متوسط ​​عودة الحلقة من -200 إلى -136.75! إنه يتعلم بالتأكيد. ما هو avg_max_q_value جيد للقارئ. لكنها إحصائية مفيدة للغاية للنظر إليها أثناء التدريب.

بعد 200000 خطوة ، يتم تدريبنا. على وحدة المعالجة المركزية رباعية النوى الخاصة بي ، يستغرق الأمر حوالي 20 دقيقة. يمكننا البحث داخل دليل date-log ، على سبيل المثال ، 06-07-18-39-log . سيكون هناك أربعة ملفات نموذج .h5 . هذه لقطة لأوزان الرسم البياني TensorFlow ، فنحن نحفظها كل 50000 خطوة لإلقاء نظرة لاحقًا على السياسة التي تعلمناها. لمشاهدته:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

لرؤية العلامات الأخرى المحتملة: python run.py --help .

الآن ، تقوم السيارة بعمل أفضل بكثير للوصول إلى الهدف المنشود. في دليل date-log ، يوجد أيضًا ملف events.out.* . هذا هو الملف الذي يخزن فيه TensorBoard بياناته. نكتب إليه باستخدام أبسط TensorBoardLogger المحدد في loggers.py. لعرض ملف الأحداث ، نحتاج إلى تشغيل خادم TensorBoard المحلي:

 tensorboard --logdir=.

--logdir يشير فقط إلى الدليل الذي توجد فيه أدلة سجل التاريخ ، في حالتنا ، سيكون هذا هو الدليل الحالي ، لذلك . . تقوم TensorBoard بطباعة عنوان URL الذي تستمع إليه. إذا فتحت http://127.0.0.1:6006 ، فسترى ثماني قطع أرض مشابهة لهذه:

تغليف

train() يقوم بكل التدريب. نقوم أولاً بإنشاء النموذج وإعادة تشغيل المخزن المؤقت. بعد ذلك ، في حلقة مشابهة جدًا لتلك الموجودة في see.py ، نتفاعل مع البيئة ونخزن الخبرات في المخزن المؤقت. المهم هو أننا نتبع سياسة إبسيلون الجشع. يمكننا دائمًا اختيار أفضل إجراء وفقًا لوظيفة $ Q $ ؛ ومع ذلك ، فإن ذلك لا يشجع الاستكشاف ، مما يضر الأداء العام. لفرض الاستكشاف باستخدام احتمالية إبسيلون ، نقوم بتنفيذ إجراءات عشوائية:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

تم ضبط Epsilon على 1٪. بعد 2000 تجربة ، تمتلئ الإعادة بما يكفي لبدء التدريب. نقوم بذلك عن طريق استدعاء fit_batch() مع مجموعة عشوائية من التجارب التي تم أخذ عينات منها من المخزن المؤقت لإعادة التشغيل:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

كل 20000 خطوة ، نقوم بتقييم النتائج وتسجيلها (التقييم باستخدام epsilon = 0 ، سياسة الجشع تمامًا):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

يتكون الكود بالكامل من 300 سطر ، ويحتوي run.py على حوالي 250 من أهمها.

يمكن للمرء أن يلاحظ وجود الكثير من المعلمات التشعبية:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

وهذا ليس كلهم. هناك أيضًا بنية شبكة - استخدمنا طبقتين مخفيتين بهما 32 خلية عصبية ، وتنشيطات ReLU ، ومحسن آدم ، ولكن هناك الكثير من الخيارات الأخرى. حتى التغييرات الصغيرة يمكن أن يكون لها تأثير كبير على التدريب. يمكن قضاء الكثير من الوقت في ضبط المعلمات الفائقة. في مسابقة OpenAI الأخيرة ، اكتشف متسابق يحتل المركز الثاني أنه من الممكن مضاعفة نقاط قوس قزح تقريبًا بعد ضبط المعامل الفائق. بطبيعة الحال ، يجب على المرء أن يتذكر أنه من السهل ارتداء الملابس الزائدة. حاليًا ، تكافح خوارزميات التعزيز لنقل المعرفة إلى بيئات مماثلة. لا تُعمم سيارة ماونتن كار الخاصة بنا على جميع أنواع الجبال في الوقت الحالي. يمكنك بالفعل تعديل بيئة OpenAI Gym ومعرفة إلى أي مدى يمكن للوكيل التعميم.

هناك تمرين آخر يتمثل في العثور على مجموعة من المعلمات الفوقية أفضل من مجموعة المعلمات الفوقية. إنه ممكن بالتأكيد. ومع ذلك ، لن تكون جولة تدريبية واحدة كافية للحكم على ما إذا كان التغيير الذي أجريته يمثل تحسينًا أم لا. عادة ما يكون هناك فرق كبير بين جولات التدريب ؛ التباين كبير. ستحتاج إلى العديد من عمليات التشغيل لتحديد ما إذا كان هناك شيء أفضل. إذا كنت ترغب في قراءة المزيد حول موضوع مهم مثل التكاثر ، فإنني أشجعك على قراءة التعلم العميق المعزز الذي يهم. بدلاً من الضبط اليدوي ، يمكننا أتمتة هذه العملية إلى حد ما - إذا كنا على استعداد لإنفاق المزيد من القوة الحاسوبية على المشكلة. تتمثل إحدى الطرق البسيطة في إعداد مجموعة واعدة من القيم لبعض المعلمات الفائقة ثم إجراء بحث في الشبكة (التحقق من مجموعاتها) ، مع إجراء التدريبات بالتوازي. الموازية نفسها هي موضوع كبير من تلقاء نفسها لأنها ضرورية للأداء العالي.

يمثل Deep $ Q $ -learning عائلة كبيرة من خوارزميات التعلم المعزز التي تستخدم تكرار القيمة. حاولنا تقريب الدالة $ Q $ ، واستخدمناها بطريقة جشعة في معظم الأوقات. هناك عائلة أخرى تستخدم سياسة التكرار. إنهم لا يركزون على تقريب دالة $ Q $ ، لكنهم يركزون على إيجاد السياسة المثلى $ π ^ * $ مباشرة. لمعرفة مكان تكرار القيمة في مشهد خوارزميات التعلم المعزز:

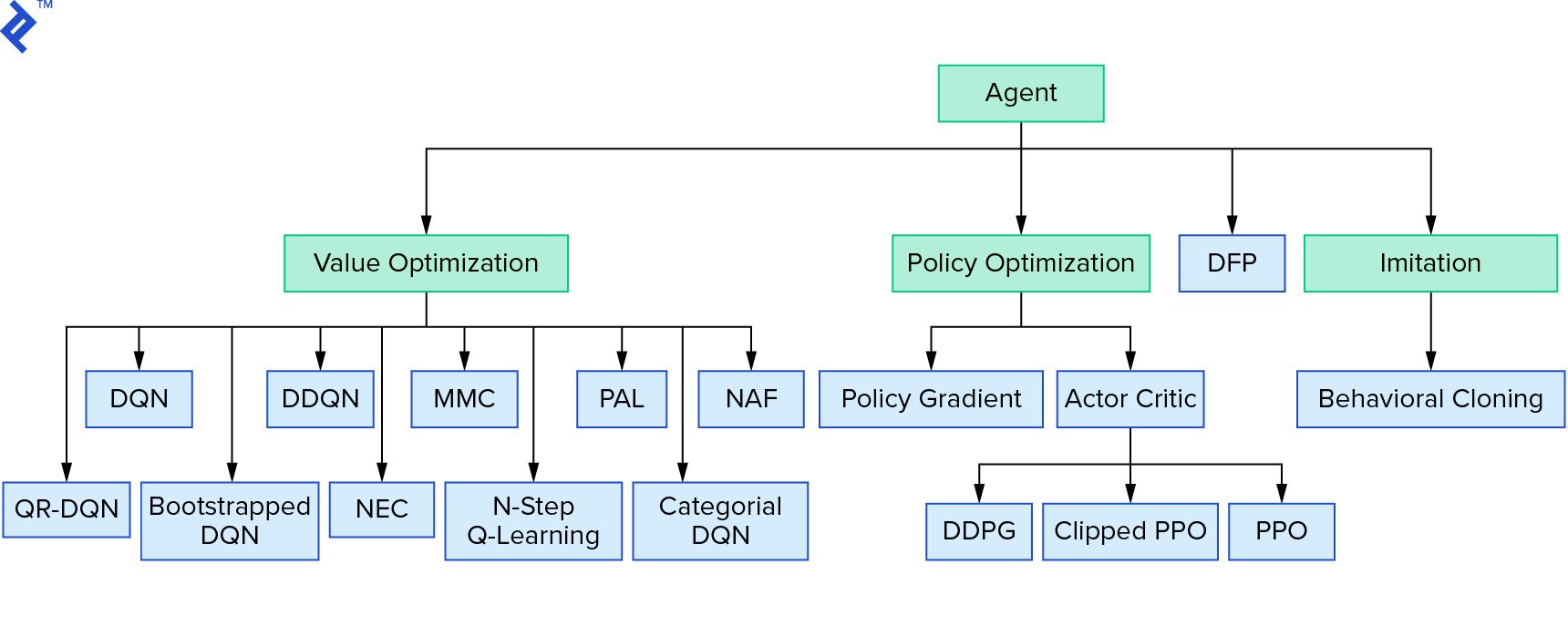
قد تكون أفكارك أن التعلم المعزز العميق يبدو هشًا. سوف تكون على حق. هناك العديد من المشاكل. يمكنك الرجوع إلى التعلم المعزز العميق الذي لا يعمل حتى الآن والتعلم المعزز لم ينجح أبدًا ، و "العميق" ساعد قليلاً فقط.

هذا يختتم البرنامج التعليمي. قمنا بتنفيذ DQN الأساسي الخاص بنا لأغراض التعلم. يمكن استخدام رمز مشابه جدًا لتحقيق أداء جيد في بعض ألعاب Atari. في التطبيقات العملية ، غالبًا ما يأخذ المرء تطبيقات عالية الأداء تم اختبارها ، على سبيل المثال ، واحد من خطوط أساس OpenAI. إذا كنت ترغب في معرفة التحديات التي يمكن أن يواجهها المرء عند محاولة تطبيق التعلم المعزز العميق في بيئة أكثر تعقيدًا ، يمكنك قراءة NIPS 2017: نهج التعلم للتشغيل. إذا كنت ترغب في معرفة المزيد في بيئة منافسة ممتعة ، فقم بإلقاء نظرة على مسابقات NIPS 2018 أو موقع Crowdai.org.

إذا كنت في طريقك لتصبح خبيرًا في التعلم الآلي وترغب في تعميق معرفتك في التعلم الخاضع للإشراف ، فراجع تحليل فيديو التعلم الآلي: التعرف على الأسماك لتجربة ممتعة في التعرف على الأسماك.