Una inmersión profunda en el aprendizaje por refuerzo

Profundicemos en el aprendizaje por refuerzo. En este artículo, abordaremos un problema concreto con las bibliotecas modernas como TensorFlow, TensorBoard, Keras y OpenAI gym. Verá cómo implementar uno de los algoritmos fundamentales llamado $Q$-aprendizaje profundo para aprender su funcionamiento interno. Con respecto al hardware, todo el código funcionará en una PC típica y usará todos los núcleos de CPU encontrados (TensorFlow se encarga de esto).

El problema se llama Mountain Car: un automóvil se encuentra en una pista unidimensional, ubicado entre dos montañas. El objetivo es conducir hasta la montaña de la derecha (llegando a la bandera). Sin embargo, el motor del automóvil no es lo suficientemente fuerte como para escalar la montaña de una sola pasada. Por lo tanto, la única forma de tener éxito es conducir de un lado a otro para generar impulso.

Se eligió este problema porque es lo suficientemente simple como para encontrar una solución con aprendizaje reforzado en minutos en un solo núcleo de CPU. Sin embargo, es lo suficientemente complejo como para ser un buen representante.

Primero, daré un breve resumen de lo que hace el aprendizaje por refuerzo en general. Luego, cubriremos los términos básicos y expresaremos nuestro problema con ellos. Después de eso, describiré el algoritmo de aprendizaje profundo de $Q$ y lo implementaremos para resolver el problema.

Conceptos básicos del aprendizaje por refuerzo

El aprendizaje por refuerzo en las palabras más simples es aprender por ensayo y error. El personaje principal se llama “agente”, que sería un automóvil en nuestro problema. El agente realiza una acción en un entorno y se le devuelve una nueva observación y una recompensa por esa acción. Se refuerzan las acciones que conducen a mayores recompensas, de ahí el nombre. Al igual que con muchas otras cosas en informática, esta también se inspiró en la observación de criaturas vivas.

Las interacciones del agente con un entorno se resumen en el siguiente gráfico:

El agente obtiene una observación y una recompensa por la acción realizada. Luego realiza otra acción y da el paso dos. El entorno ahora devuelve una observación y una recompensa (probablemente) ligeramente diferentes. Esto continúa hasta que se alcanza el estado terminal, que se indica mediante el envío de "hecho" a un agente. La secuencia completa de observaciones > acciones > próximas_observaciones > recompensas se denomina episodio (o trayectoria).

Volviendo a nuestro Mountain Car: nuestro coche es un agente. El entorno es un mundo de caja negra de montañas unidimensionales. La acción del automóvil se reduce a un solo número: si es positivo, el motor empuja al automóvil hacia la derecha. Si es negativo, empuja el coche hacia la izquierda. El agente percibe un entorno a través de una observación: la posición X y la velocidad del coche. Si queremos que nuestro coche circule por la cima de la montaña, definimos la recompensa de forma conveniente: El agente obtiene -1 a su recompensa por cada paso en el que no haya llegado a la meta. Cuando llega a la meta, el episodio termina. Entonces, de hecho, el agente es castigado por no estar en la posición que queremos que esté. Cuanto más rápido lo alcance, mejor para él. El objetivo del agente es maximizar la recompensa total, que es la suma de las recompensas de un episodio. Entonces, si llega al punto deseado después de, por ejemplo, 110 pasos, recibe un retorno total de -110, lo que sería un gran resultado para Mountain Car, porque si no llega a la meta, entonces es castigado con 200 pasos. (por lo tanto, un retorno de -200).

Esta es toda la formulación del problema. Ahora, podemos dárselo a los algoritmos, que ya son lo suficientemente potentes como para resolver este tipo de problemas en cuestión de minutos (si están bien sintonizados). Vale la pena señalar que no le decimos al agente cómo lograr el objetivo. Ni siquiera proporcionamos pistas (heurísticas). El agente encontrará una manera (una política) de ganar por su cuenta.

Configuración del entorno

Primero, copie todo el código del tutorial en su disco:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Ahora, necesitamos instalar los paquetes de Python que usaremos. Para no instalarlos en su espacio de usuario (y correr el riesgo de colisiones), lo limpiaremos y los instalaremos en el entorno de conda. Si no tiene conda instalado, siga https://conda.io/docs/user-guide/install/index.html.

Para crear nuestro entorno conda:

 conda create -n tutorial python=3.6.5 -y

Para activarlo:

 source activate tutorial

Debería ver (tutorial) cerca de su indicador en el shell. Significa que está activo un entorno conda con el nombre “tutorial”. De ahora en adelante, todos los comandos deben ejecutarse dentro de ese entorno conda.

Ahora, podemos instalar todas las dependencias en nuestro entorno hermetic conda:

 pip install -r requirements.txt

Hemos terminado con la instalación, así que vamos a ejecutar algo de código. No necesitamos implementar el entorno de Mountain Car nosotros mismos; la biblioteca OpenAI Gym proporciona esa implementación. Veamos un agente aleatorio (un agente que realiza acciones aleatorias) en nuestro entorno:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Este es el archivo see.py ; para ejecutarlo, ejecuta:

 python see.py

Deberías ver un automóvil yendo y viniendo aleatoriamente. Cada episodio constará de 200 pasos; el retorno total será -200.

Ahora necesitamos reemplazar las acciones aleatorias con algo mejor. Hay muchos algoritmos que uno podría usar. Para un tutorial introductorio, creo que un enfoque llamado aprendizaje profundo de $Q$ es una buena opción. Comprender ese método brinda una base sólida para aprender otros enfoques.

Aprendizaje $Q$ profundo

El algoritmo que utilizaremos fue descrito por primera vez en 2013 por Mnih et al. en Playing Atari with Deep Reinforcement Learning y pulido dos años más tarde en Human-level control through deep booster learning. Muchos otros trabajos se basan en esos resultados, incluido el actual algoritmo de última generación Rainbow (2017):

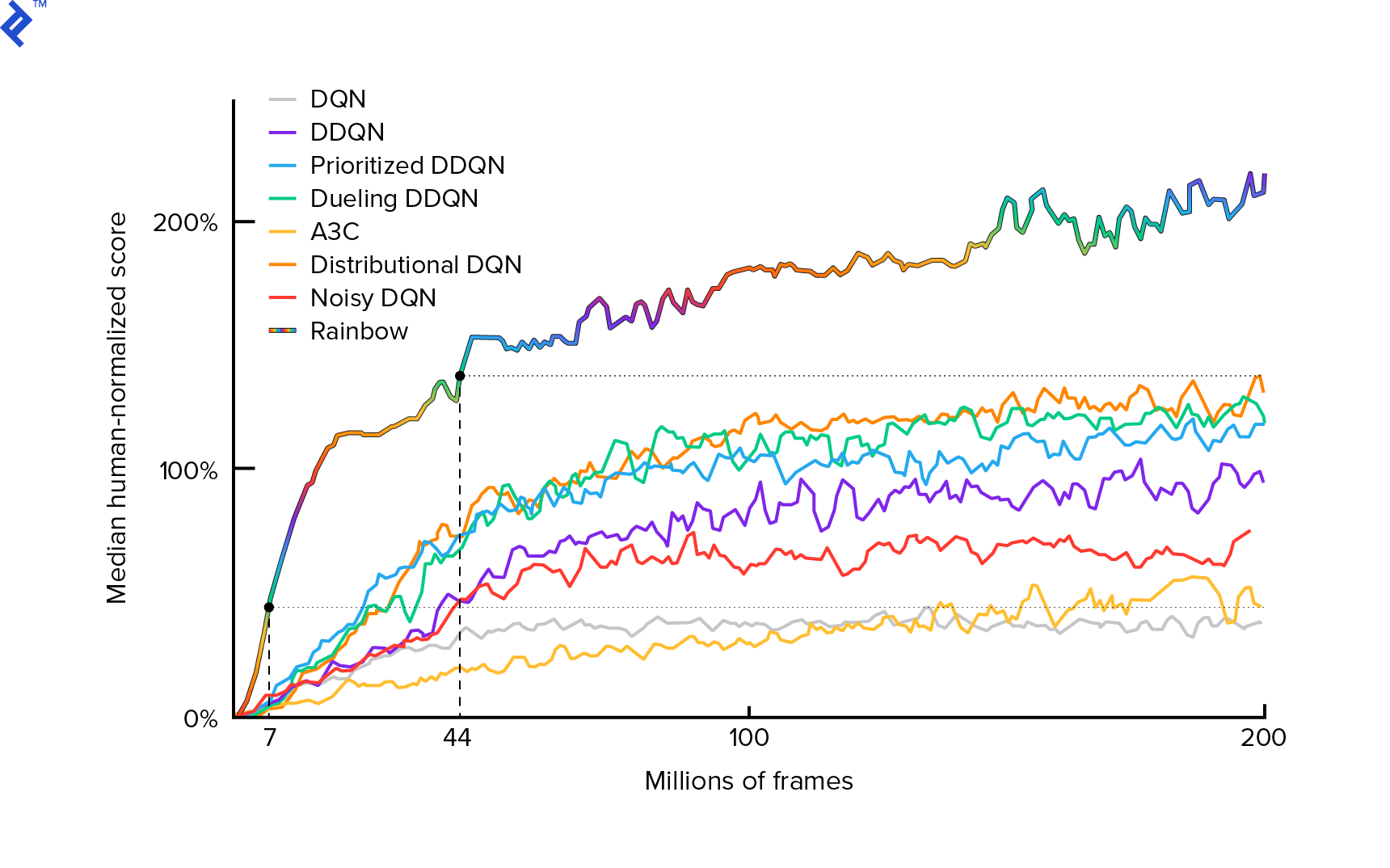
Rainbow logra un rendimiento sobrehumano en muchos juegos de Atari 2600. Nos centraremos en la versión básica de DQN, con la menor cantidad posible de mejoras adicionales, para mantener este tutorial en un tamaño razonable.

Una política, normalmente denominada $π(s)$, es una función que devuelve probabilidades de realizar acciones individuales en un estado dado $s$. Entonces, por ejemplo, una póliza aleatoria de Mountain Car regresa para cualquier estado: 50% a la izquierda, 50% a la derecha. Durante el juego, tomamos muestras de esa política (distribución) para obtener acciones reales.

$Q$-aprendizaje (Q es para Calidad) se refiere a la función de valor de acción denotada $Q_π(s, a)$. Devuelve la rentabilidad total de un estado dado $s$, eligiendo la acción $a$, siguiendo una política concreta $π$. El retorno total es la suma de todas las recompensas en un episodio (trayectoria).

Si conociéramos la función $Q$ óptima, denominada $Q^*$, podríamos resolver el juego fácilmente. Simplemente seguiríamos las acciones con el valor más alto de $Q^*$, es decir, el rendimiento esperado más alto. Esto garantiza que alcanzaremos la mayor rentabilidad posible.

Sin embargo, a menudo no sabemos $Q^*$. En tales casos, podemos aproximarnos, o "aprender", a partir de las interacciones con el medio ambiente. Esta es la parte "$Q$-learning" del nombre. También incluye la palabra "profundo" porque, para aproximar esa función, usaremos redes neuronales profundas, que son aproximadores universales de funciones. Las redes neuronales profundas que se aproximan a los valores de $Q$ se denominaron Deep Q-Networks (DQN). En entornos simples (con la cantidad de estados que caben en la memoria), se podría usar una tabla en lugar de una red neuronal para representar la función $Q$, en cuyo caso se denominaría "aprendizaje $Q$ tabular".

Así que nuestro objetivo ahora es aproximar la función $Q^*$. Usaremos la ecuación de Bellman:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ es el estado después de $s$. $γ$ (gamma), normalmente 0,99, es un factor de descuento (es un hiperparámetro). Pone un peso menor en las recompensas futuras (porque son menos seguras que las recompensas inmediatas con nuestro $Q$ imperfecto). La ecuación de Bellman es fundamental para el aprendizaje profundo de $Q$. Dice que el valor de $Q$ para un estado y acción dados es una recompensa $r$ recibida después de realizar la acción $a$ más el valor de $Q$ más alto para el estado en el que aterrizamos en $s'$. El más alto es en el sentido de que estamos eligiendo una acción $a'$, que conduce al rendimiento total más alto de $s'$.

Con la ecuación de Bellman, podemos usar el aprendizaje supervisado para aproximar $Q^*$. La función $Q$ estará representada (parametrizada) por los pesos de la red neuronal indicados como $θ$ (theta). Una implementación sencilla tomaría un estado y una acción cuando la red ingrese y emita el valor Q. La ineficiencia es que si queremos conocer los valores de $Q$ para todas las acciones en un estado dado, necesitamos llamar a $Q$ tantas veces como acciones haya. Hay una forma mucho mejor: tomar solo el estado como entrada y salida de valores $Q$ para todas las acciones posibles. Gracias a eso, podemos obtener valores de $Q$ para todas las acciones en un solo paso hacia adelante.

Comenzamos a entrenar la red $Q$ con pesos aleatorios. Del entorno obtenemos muchas transiciones (o “experiencias”). Estas son tuplas de (estado, acción, siguiente estado, recompensa) o, en resumen, ($s$, $a$, $s'$, $r$). Almacenamos miles de ellos en un búfer de anillo llamado "repetición de experiencia". Luego, tomamos muestras de experiencias de ese búfer con el deseo de que la ecuación de Bellman se mantenga para ellos. Podríamos habernos saltado el búfer y aplicado las experiencias una por una (esto se llama "en línea" o "en la política"); el problema es que las experiencias posteriores están altamente correlacionadas entre sí y DQN entrena mal cuando esto ocurre. Es por eso que se introdujo la repetición de la experiencia (un enfoque "fuera de línea", "fuera de la política") para romper esta correlación de datos. El código de nuestra implementación de búfer de anillo más simple se puede encontrar en el archivo replay_buffer.py , lo animo a leerlo.

Al principio, dado que los pesos de nuestras redes neuronales eran aleatorios, el valor del lado izquierdo de la ecuación de Bellman estará lejos del lado derecho. La diferencia al cuadrado será nuestra función de pérdida. Minimizaremos la función de pérdida cambiando los pesos de la red neuronal $θ$. Escribamos nuestra función de pérdida:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

Es una ecuación de Bellman reescrita. Digamos que probamos una experiencia ($s$, izquierda, $s'$, -1) de la repetición de la experiencia Mountain Car. Hacemos un pase hacia adelante a través de nuestra red $Q$ con el estado $s$ y para action left nos da -120, por ejemplo. Entonces, $Q(s, \textrm{izquierda}) = -120$. Luego alimentamos $s'$ a la red, lo que nos da, por ejemplo, -130 para la izquierda y -122 para la derecha. Claramente, la mejor acción para $s'$ es correcta, por lo tanto, $\textrm{max}_{a'}Q(s', a') = -122$. Sabemos $r$, esta es la recompensa real, que fue -1. Entonces, nuestra predicción de la red $Q$ fue un poco incorrecta, porque $L(θ) = [-120 - 1 + 0.99 ⋅ 122]^2 = (-0.22^2) = 0.0484$. Así que propagamos el error hacia atrás y corregimos ligeramente los pesos $θ$. Si tuviéramos que calcular la pérdida nuevamente para la misma experiencia, ahora sería menor.

Una observación importante antes de pasar al código. Notemos que, para actualizar nuestro DQN, haremos dos pases hacia adelante en DQN... mismo. Esto a menudo conduce a un aprendizaje inestable. Para paliar eso, para la próxima predicción $Q$ del estado, no usamos el mismo DQN. Usamos una versión anterior, que en el código se llama target_model (en lugar de model , siendo el DQN principal). Gracias a eso, tenemos un objetivo estable. Actualizamos target_model configurándolo para model pesos cada 1000 pasos. Pero model actualiza cada paso.

Veamos el código que crea el modelo DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Primero, la función toma las dimensiones del espacio de acción y observación del entorno dado de OpenAI Gym. Es necesario saber, por ejemplo, cuántas salidas tendrá nuestra red. Debe ser igual al número de acciones. Las acciones son una codificada en caliente:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Entonces (p. ej.) la izquierda será [1, 0] y la derecha será [0, 1].

Podemos ver que las observaciones se pasan como entrada. También pasamos action_mask como segunda entrada. ¿Por qué? Al calcular $Q(s,a)$, necesitamos saber el valor de $Q$ solo para una acción determinada, no para todas. action_mask contiene 1 para las acciones que queremos pasar a la salida de DQN. Si action_mask tiene 0 para alguna acción, entonces el valor $Q$ correspondiente se pondrá a cero en la salida. La capa filtered_output está haciendo eso. Si queremos todos los valores de $Q$ (para el cálculo máximo), podemos pasarlos todos.

El código usa keras.layers.Dense para definir una capa completamente conectada. Keras es una biblioteca de Python para la abstracción de alto nivel además de TensorFlow. Debajo del capó, Keras crea un gráfico TensorFlow, con sesgos, inicialización de peso adecuada y otras cosas de bajo nivel. Podríamos haber usado TensorFlow sin procesar para definir el gráfico, pero no será una sola línea.

Entonces las observaciones se pasan a la primera capa oculta, con activaciones de ReLU (unidad lineal rectificada). ReLU(x) es solo una función $\textrm{max}(0, x)$. Esa capa está completamente conectada con una segunda idéntica, hidden_2 . La capa de salida reduce el número de neuronas al número de acciones. Al final, tenemos filtered_output , que simplemente multiplica la salida con action_mask .

Para encontrar pesos $θ$, usaremos un optimizador llamado "Adam" con una pérdida de error cuadrático medio.

Al tener un modelo, podemos usarlo para predecir los valores de $Q$ para las observaciones de estado dadas:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Queremos valores $Q$ para todas las acciones, por lo que action_mask es un vector de unos.

Para hacer el entrenamiento real, usaremos fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

El lote contiene BATCH_SIZE experiencias. next_q_values ​​es $Q(s, a)$. q_values ​​es $r + γ \space \textrm{max}_{a'}Q(s', a')$ de la ecuación de Bellman. Las acciones que tomamos están codificadas en caliente y pasadas como action_mask a la entrada cuando llamamos a model.fit() . $y$ es una letra común para un "objetivo" en el aprendizaje supervisado. Aquí estamos pasando los q_values . Hago q_values[:. None] q_values[:. None] para aumentar la dimensión de la matriz porque debe corresponder a la dimensión de la matriz one_hot_actions . Esto se llama notación de corte si desea leer más al respecto.

Devolvemos la pérdida para guardarla en el archivo de registro de TensorBoard y luego visualizar. Hay muchas otras cosas que monitorearemos: cuántos pasos por segundo damos, el uso total de RAM, cuál es el retorno promedio de los episodios, etc. Veamos esos gráficos.

Corriendo

Para visualizar el archivo de registro de TensorBoard, primero debemos tener uno. Así que vamos a ejecutar el entrenamiento:

 python run.py

Esto primero imprimirá el resumen de nuestro modelo. Luego creará un directorio de registro con la fecha actual y comenzará el entrenamiento. Cada 2000 pasos, se imprimirá una línea de registro similar a esta:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Cada 20.000, evaluaremos nuestro modelo en 10.000 pasos:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

¡Después de 677 episodios y 120 000 pasos, el rendimiento promedio de los episodios mejoró de -200 a -136,75! Definitivamente es aprender. Lo que es avg_max_q_value lo dejo como un buen ejercicio para el lector. Pero es una estadística muy útil para observar durante el entrenamiento.

Después de 200.000 pasos, nuestro entrenamiento está terminado. En mi CPU de cuatro núcleos, tarda unos 20 minutos. Podemos mirar dentro del directorio date-log , por ejemplo, 06-07-18-39-log . Habrá cuatro archivos de modelo con la extensión .h5 . Esta es una instantánea de los pesos de los gráficos de TensorFlow, los guardamos cada 50 000 pasos para luego ver la política que aprendimos. Para verlo:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Para ver los otros indicadores posibles: python run.py --help .

Ahora, el automóvil está haciendo un trabajo mucho mejor para alcanzar la meta deseada. En el directorio date-log , también se encuentra el archivo events.out.* . Este es el archivo donde TensorBoard almacena sus datos. Escribimos en él usando el TensorBoardLogger más simple definido en loggers.py. Para ver el archivo de eventos, necesitamos ejecutar el servidor local de TensorBoard:

 tensorboard --logdir=.

--logdir simplemente apunta al directorio en el que hay directorios de registro de fechas, en nuestro caso, este será el directorio actual, por lo que . . TensorBoard imprime la URL en la que está escuchando. Si abre http://127.0.0.1:6006, debería ver ocho gráficos similares a estos:

Terminando

train() hace todo el entrenamiento. Primero creamos el modelo y reproducimos el búfer. Luego, en un bucle muy similar al de see.py , interactuamos con el entorno y almacenamos experiencias en el búfer. Lo importante es que sigamos una política de avaricia épsilon. Siempre podemos elegir la mejor acción según la función $Q$; sin embargo, eso desalienta la exploración, lo que perjudica el rendimiento general. Entonces, para hacer cumplir la exploración con probabilidad épsilon, realizamos acciones aleatorias:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon se ajustó al 1%. Después de 2000 experiencias, la repetición se llena lo suficiente como para comenzar el entrenamiento. Lo hacemos llamando a fit_batch() con un lote aleatorio de experiencias muestreadas del búfer de reproducción:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Cada 20.000 pasos, evaluamos y registramos los resultados (la evaluación es con epsilon = 0 , política totalmente codiciosa):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

El código completo tiene unas 300 líneas y run.py contiene unas 250 de las más importantes.

Uno puede notar que hay muchos hiperparámetros:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Y eso no es todo de ellos. También hay una arquitectura de red: usamos dos capas ocultas con 32 neuronas, activaciones ReLU y el optimizador Adam, pero hay muchas otras opciones. Incluso los pequeños cambios pueden tener un gran impacto en el entrenamiento. Se puede dedicar mucho tiempo a ajustar los hiperparámetros. En una competencia reciente de OpenAI, un concursante que quedó en segundo lugar descubrió que es posible casi duplicar la puntuación de Rainbow después de ajustar los hiperparámetros. Naturalmente, hay que recordar que es fácil sobreajustar. Actualmente, los algoritmos de refuerzo están luchando con la transferencia de conocimiento a entornos similares. Nuestro Mountain Car no se generaliza a todo tipo de montañas en este momento. De hecho, puede modificar el entorno de OpenAI Gym y ver hasta dónde puede generalizar el agente.

Otro ejercicio será encontrar un mejor conjunto de hiperparámetros que el mío. Definitivamente es posible. Sin embargo, una carrera de entrenamiento no será suficiente para juzgar si su cambio es una mejora. Por lo general, hay una gran diferencia entre las carreras de entrenamiento; la varianza es grande. Necesitaría muchas ejecuciones para determinar que algo es mejor. Si desea leer más sobre un tema tan importante como la reproducibilidad, lo animo a leer Deep Reinforcement Learning that Matters. En lugar de ajustar a mano, podemos automatizar este proceso hasta cierto punto, si estamos dispuestos a gastar más poder de cómputo en el problema. Un enfoque simple es preparar un rango prometedor de valores para algunos hiperparámetros y luego ejecutar una búsqueda en cuadrícula (comprobando sus combinaciones), con entrenamientos que se ejecutan en paralelo. La paralelización en sí es un gran tema en sí mismo, ya que es crucial para un alto rendimiento.

Deep $Q$-learning representa una gran familia de algoritmos de aprendizaje por refuerzo que utilizan la iteración de valor. Intentamos aproximarnos a la función $Q$, y la usamos de manera codiciosa la mayor parte del tiempo. Hay otra familia que utiliza la iteración de políticas. No se enfocan en aproximar la función $Q$, sino en encontrar la política óptima $π^*$ directamente. Para ver dónde encaja la iteración de valor en el panorama de los algoritmos de aprendizaje por refuerzo:

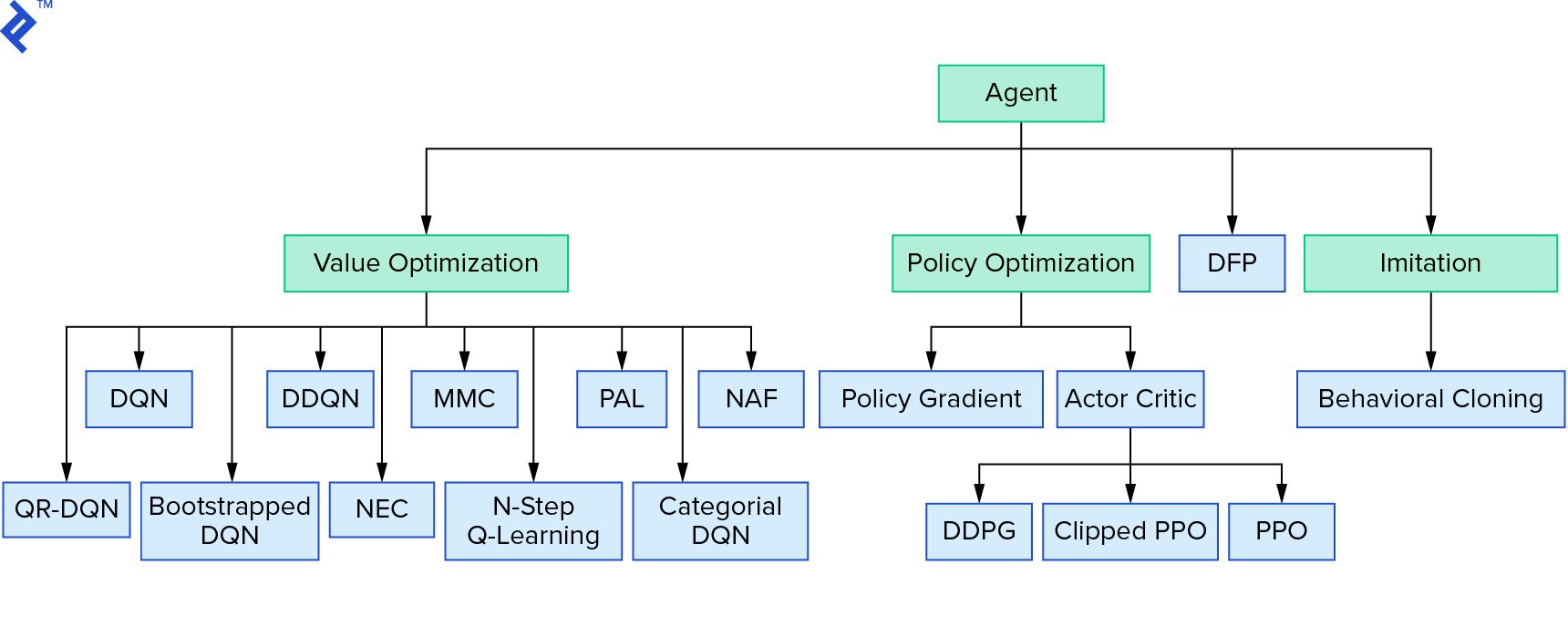
Sus pensamientos podrían ser que el aprendizaje de refuerzo profundo parece frágil. Tendrás razón; Hay muchos problemas. Puede referirse a Aprendizaje de refuerzo profundo no funciona todavía y Aprendizaje de refuerzo nunca funcionó, y 'profundo' solo ayudó un poco.

Esto concluye el tutorial. Implementamos nuestro propio DQN básico con fines de aprendizaje. Se puede usar un código muy similar para lograr un buen rendimiento en algunos de los juegos de Atari. En aplicaciones prácticas, a menudo se toman implementaciones probadas y de alto rendimiento, por ejemplo, una de las líneas base de OpenAI. Si desea ver los desafíos que se pueden enfrentar al tratar de aplicar el aprendizaje de refuerzo profundo en un entorno más complejo, puede leer Nuestro enfoque NIPS 2017: Aprender a ejecutar. Si desea obtener más información en un entorno de competencia divertido, eche un vistazo a NIPS 2018 Competitions o crowdai.org.

Si está en camino de convertirse en un experto en aprendizaje automático y le gustaría profundizar su conocimiento en el aprendizaje supervisado, consulte Análisis de video de aprendizaje automático: Identificación de peces para un experimento divertido sobre la identificación de peces.