Ein tiefer Einblick in Reinforcement Learning

Lassen Sie uns einen tiefen Einblick in das bestärkende Lernen nehmen. In diesem Artikel gehen wir ein konkretes Problem mit modernen Bibliotheken wie TensorFlow, TensorBoard, Keras und OpenAI Gym an. Sie werden sehen, wie Sie einen der grundlegenden Algorithmen namens tiefes $Q$-Lernen implementieren, um seine inneren Abläufe zu lernen. In Bezug auf die Hardware funktioniert der gesamte Code auf einem typischen PC und verwendet alle gefundenen CPU-Kerne (dies wird standardmäßig von TensorFlow gehandhabt).

Das Problem heißt Mountain Car: Ein Auto befindet sich auf einer eindimensionalen Strecke, positioniert zwischen zwei Bergen. Ziel ist es, den Berg rechts hochzufahren (Erreichen der Fahne). Allerdings ist der Motor des Autos nicht stark genug, um den Berg in einem einzigen Durchgang zu erklimmen. Daher ist der einzige Weg zum Erfolg, hin und her zu fahren, um Schwung aufzubauen.

Dieses Problem wurde gewählt, weil es einfach genug ist, eine Lösung mit Verstärkungslernen in Minuten auf einem einzelnen CPU-Kern zu finden. Es ist jedoch komplex genug, um ein guter Repräsentant zu sein.

Zuerst werde ich eine kurze Zusammenfassung darüber geben, was Reinforcement Learning im Allgemeinen bewirkt. Dann werden wir grundlegende Begriffe behandeln und unser Problem damit ausdrücken. Danach werde ich den tiefen $Q$-Lernalgorithmus beschreiben und wir werden ihn implementieren, um das Problem zu lösen.

Grundlagen des Verstärkungslernens

Reinforcement Learning ist im einfachsten Sinne Lernen durch Versuch und Irrtum. Die Hauptfigur wird „Agent“ genannt, was in unserem Problem ein Auto wäre. Der Agent führt eine Aktion in einer Umgebung aus und erhält eine neue Beobachtung und eine Belohnung für diese Aktion. Aktionen, die zu größeren Belohnungen führen, werden verstärkt, daher der Name. Wie bei vielen anderen Dingen in der Informatik wurde auch dieses durch die Beobachtung von Lebewesen inspiriert.

Die Interaktionen des Agenten mit einer Umgebung sind in der folgenden Grafik zusammengefasst:

Der Agent erhält eine Beobachtung und eine Belohnung für die durchgeführte Aktion. Dann führt es eine weitere Aktion aus und führt Schritt zwei aus. Die Umgebung gibt jetzt eine (wahrscheinlich) etwas andere Beobachtung und Belohnung zurück. Dies wird fortgesetzt, bis der Endzustand erreicht ist, was durch das Senden von „Fertig“ an einen Agenten signalisiert wird. Die gesamte Folge von Beobachtungen > Aktionen > nächste_Beobachtungen > Belohnungen wird als Episode (oder Trajektorie) bezeichnet.

Zurück zu unserem Mountain Car: Unser Auto ist ein Agent. Die Umgebung ist eine Black-Box-Welt aus eindimensionalen Bergen. Die Aktion des Autos läuft auf nur eine Zahl hinaus: Wenn positiv, schiebt der Motor das Auto nach rechts. Wenn negativ, schiebt es das Auto nach links. Der Agent nimmt eine Umgebung durch eine Beobachtung wahr: die X-Position und Geschwindigkeit des Autos. Wenn wir wollen, dass unser Auto auf den Berg fährt, definieren wir die Belohnung auf bequeme Weise: Der Agent erhält -1 auf seine Belohnung für jeden Schritt, bei dem er das Ziel nicht erreicht hat. Wenn es das Ziel erreicht, endet die Episode. Tatsächlich wird der Agent dafür bestraft, dass er nicht in einer Position ist, die wir uns wünschen. Je schneller er es erreicht, desto besser für ihn. Das Ziel des Agenten ist es, die Gesamtbelohnung zu maximieren, die die Summe der Belohnungen aus einer Episode ist. Erreicht es also nach zB 110 Schritten den gewünschten Punkt, erhält es eine Gesamtrendite von -110, was für Mountain Car ein tolles Ergebnis wäre, denn wenn es das Ziel nicht erreicht, wird es mit 200 Schritten bestraft (daher eine Rendite von -200).

Das ist die ganze Problemformulierung. Jetzt können wir es den Algorithmen geben, die bereits leistungsfähig genug sind, um solche Probleme in wenigen Minuten zu lösen (wenn sie gut abgestimmt sind). Es ist erwähnenswert, dass wir dem Agenten nicht sagen, wie er das Ziel erreichen soll. Wir geben nicht einmal Hinweise (Heuristik). Der Agent wird einen Weg (eine Richtlinie) finden, um selbst zu gewinnen.

Einrichten der Umgebung

Kopieren Sie zuerst den gesamten Tutorial-Code auf Ihre Festplatte:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Jetzt müssen wir Python-Pakete installieren, die wir verwenden werden. Um sie nicht in Ihrem Benutzerbereich zu installieren (und Kollisionen zu riskieren), werden wir sie sauber machen und sie in der Conda-Umgebung installieren. Wenn Sie conda nicht installiert haben, folgen Sie bitte https://conda.io/docs/user-guide/install/index.html.

So erstellen Sie unsere Conda-Umgebung:

 conda create -n tutorial python=3.6.5 -y

Um es zu aktivieren:

 source activate tutorial

Sie sollten (tutorial) in der Nähe Ihrer Eingabeaufforderung in der Shell sehen. Das bedeutet, dass eine Conda-Umgebung mit dem Namen „tutorial“ aktiv ist. Von nun an sollten alle Befehle in dieser Conda-Umgebung ausgeführt werden.

Jetzt können wir alle Abhängigkeiten in unserer hermetischen Conda-Umgebung installieren:

 pip install -r requirements.txt

Wir sind mit der Installation fertig, also lassen Sie uns etwas Code ausführen. Wir müssen die Mountain Car-Umgebung nicht selbst implementieren; Die OpenAI Gym-Bibliothek stellt diese Implementierung bereit. Sehen wir uns einen zufälligen Agenten (einen Agenten, der zufällige Aktionen ausführt) in unserer Umgebung an:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Dies ist die see.py -Datei; Um es auszuführen, führen Sie Folgendes aus:

 python see.py

Sie sollten ein Auto sehen, das willkürlich hin und her fährt. Jede Folge besteht aus 200 Schritten; die Gesamtrendite beträgt -200.

Jetzt müssen wir zufällige Aktionen durch etwas Besseres ersetzen. Es gibt viele Algorithmen, die man verwenden könnte. Für ein einführendes Tutorial denke ich, dass ein Ansatz namens tiefes $Q$-Lernen gut passt. Das Verständnis dieser Methode bietet eine solide Grundlage für das Erlernen anderer Ansätze.

Tiefes $Q$-Lernen

Der Algorithmus, den wir verwenden werden, wurde erstmals 2013 von Mnih et al. beschrieben. in Playing Atari with Deep Reinforcement Learning und polierte zwei Jahre später in Human-Level Control through Deep Reinforcement Learning. Viele andere Arbeiten bauen auf diesen Ergebnissen auf, einschließlich des aktuellen State-of-the-Art-Algorithmus Rainbow (2017):

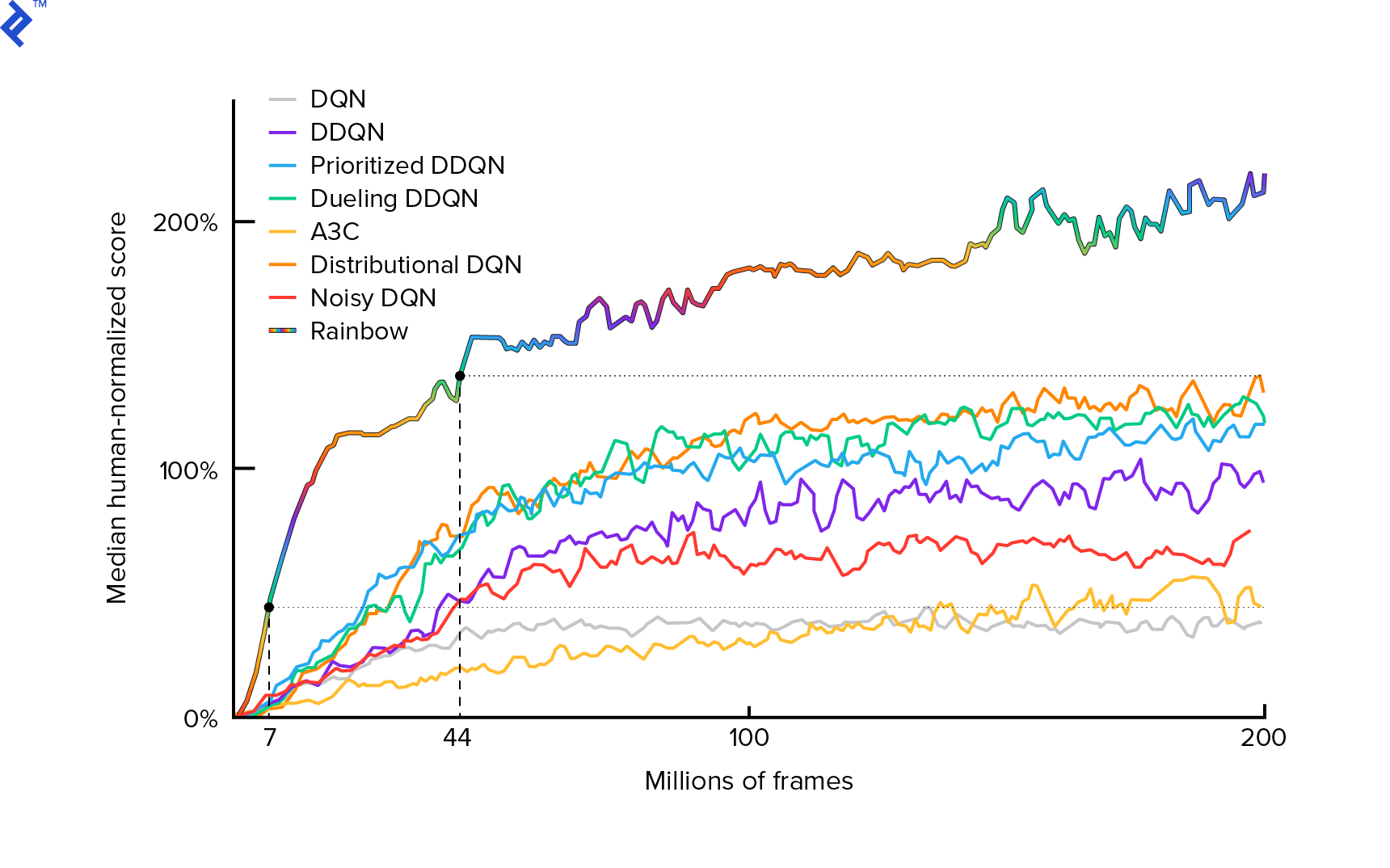
Rainbow erreicht bei vielen Atari 2600-Spielen übermenschliche Leistungen. Wir konzentrieren uns auf die grundlegende DQN-Version mit einer möglichst geringen Anzahl zusätzlicher Verbesserungen, um dieses Tutorial in einem angemessenen Umfang zu halten.

Eine Richtlinie, typischerweise mit $π(s)$ bezeichnet, ist eine Funktion, die Wahrscheinlichkeiten zurückgibt, einzelne Aktionen in einem gegebenen Zustand $s$ durchzuführen. So ergibt beispielsweise eine zufällige Mountain Car-Police für jeden Zustand: 50 % links, 50 % rechts. Während des Spiels nehmen wir Stichproben von dieser Richtlinie (Verteilung) vor, um echte Aktionen zu erhalten.

$Q$-Lernen (Q steht für Qualität) bezieht sich auf die Aktionswertfunktion mit der Bezeichnung $Q_π(s, a)$. Es gibt die Gesamtrendite von einem gegebenen Zustand $s$ zurück, wobei die Aktion $a$ gewählt wird und einer konkreten Richtlinie $π$ folgt. Die Gesamtrendite ist die Summe aller Belohnungen in einer Episode (Trajektorie).

Wenn wir die optimale $Q$-Funktion mit der Bezeichnung $Q^*$ kennen würden, könnten wir das Spiel leicht lösen. Wir würden einfach die Aktionen mit dem höchsten Wert von $Q^*$ verfolgen, dh der höchsten erwarteten Rendite. Dies garantiert, dass wir die höchstmögliche Rendite erzielen.

Allerdings kennen wir $Q^*$ oft nicht. In solchen Fällen können wir es aus den Wechselwirkungen mit der Umgebung annähern – oder „lernen“. Das ist der Teil „$Q$-learning“ im Namen. Es gibt auch das Wort „deep“ darin, weil wir, um diese Funktion zu approximieren, tiefe neuronale Netze verwenden werden, die universelle Funktionsapproximatoren sind. Tiefe neuronale Netze, die $Q$-Werte annähern, wurden als Deep Q-Networks (DQN) bezeichnet. In einfachen Umgebungen (mit der Anzahl der Zustände, die in den Speicher passen) könnte man einfach eine Tabelle anstelle eines neuronalen Netzes verwenden, um die $Q$-Funktion darzustellen, in diesem Fall würde sie „tabular $Q$-learning“ heißen.

Unser Ziel ist es nun, die $Q^*$-Funktion zu approximieren. Wir verwenden die Bellman-Gleichung:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ ist der Zustand nach $s$. $γ$ (Gamma), normalerweise 0,99, ist ein Diskontfaktor (es ist ein Hyperparameter). Es legt ein geringeres Gewicht auf zukünftige Belohnungen (weil sie weniger sicher sind als sofortige Belohnungen mit unserem unvollkommenen $Q$). Die Bellman-Gleichung ist zentral für tiefes $Q$-Lernen. Es besagt, dass der $Q$-Wert für einen bestimmten Zustand und eine gegebene Aktion eine Belohnung ist, die $r$ erhält, nachdem er die Aktion $a$ ausgeführt hat, plus dem höchsten $Q$-Wert für den Zustand, in dem wir in $s'$ landen. Das Höchste ist in gewissem Sinne, dass wir eine Aktion $a'$ wählen, die zu der höchsten Gesamtrendite von $s'$ führt.

Mit der Bellman-Gleichung können wir überwachtes Lernen verwenden, um $Q^*$ anzunähern. Die $Q$-Funktion wird durch neuronale Netzwerkgewichte dargestellt (parametrisiert), die als $θ$ (Theta) bezeichnet werden. Eine einfache Implementierung würde einen Zustand und eine Aktion als Netzwerkeingang annehmen und den Q-Wert ausgeben. Die Ineffizienz besteht darin, dass wir, wenn wir $Q$-Werte für alle Aktionen in einem bestimmten Zustand wissen wollen, $Q$ so oft aufrufen müssen, wie es Aktionen gibt. Es gibt einen viel besseren Weg: nur den Zustand als Eingabe zu nehmen und $Q$-Werte für alle möglichen Aktionen auszugeben. Dank dessen können wir $Q$-Werte für alle Aktionen in nur einem Vorwärtsdurchgang erhalten.

Wir beginnen mit dem Training des $Q$-Netzwerks mit zufälligen Gewichtungen. Aus der Umgebung erhalten wir viele Übergänge (oder „Erfahrungen“). Dies sind Tupel von (Zustand, Aktion, nächster Zustand, Belohnung) oder kurz ($s$, $a$, $s'$, $r$). Wir speichern Tausende von ihnen in einem Ringpuffer namens „Experience Replay“. Dann proben wir Erfahrungen aus diesem Puffer mit dem Wunsch, dass die Bellman-Gleichung für sie gelten wird. Wir hätten den Puffer überspringen und Erfahrungen einzeln anwenden können (dies wird „online“ oder „on-policy“ genannt); Das Problem ist, dass nachfolgende Erfahrungen stark miteinander korrelieren und DQN schlecht trainiert, wenn dies auftritt. Aus diesem Grund wurde die Erfahrungswiedergabe eingeführt (ein „offline“, „off-policy“-Ansatz), um diese Datenkorrelation aufzubrechen. Den Code unserer einfachsten Ringpufferimplementierung finden Sie in der Datei replay_buffer.py , ich ermutige Sie, ihn zu lesen.

Da unsere neuronalen Netzwerkgewichtungen zu Beginn zufällig waren, wird der Wert auf der linken Seite der Bellman-Gleichung weit von der rechten Seite entfernt sein. Die quadrierte Differenz ist unsere Verlustfunktion. Wir werden die Verlustfunktion minimieren, indem wir die Gewichte des neuronalen Netzwerks $θ$ ändern. Schreiben wir unsere Verlustfunktion auf:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

Es ist eine umgeschriebene Bellman-Gleichung. Angenommen, wir haben ein Erlebnis ($s$, left, $s'$, -1) aus der Wiedergabe des Mountain Car-Erlebnisses abgetastet. Wir führen einen Vorwärtsdurchgang durch unser $Q$-Netzwerk mit dem Zustand $s$ durch und für die linke Aktion erhalten wir zum Beispiel -120. Also $Q(s, \textrm{links}) = -120$. Dann speisen wir $s'$ in das Netzwerk ein, was uns zB -130 für links und -122 für rechts liefert. Die beste Aktion für $s'$ ist also eindeutig richtig, also $\textrm{max}_{a'}Q(s', a') = -122$. Wir wissen $r$, das ist die eigentliche Belohnung, die -1 war. Unsere $Q$-Netzwerkvorhersage war also etwas falsch, denn $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Also propagieren wir den Fehler rückwärts und korrigieren die Gewichte $θ$ leicht. Würden wir den Verlust für dieselbe Erfahrung noch einmal berechnen, wäre er jetzt geringer.

Eine wichtige Beobachtung, bevor wir zum Code übergehen. Beachten Sie, dass wir zum Aktualisieren unseres DQN zwei Vorwärtsdurchläufe auf DQN… selbst durchführen werden. Dies führt oft zu instabilem Lernen. Um dies zu verringern, verwenden wir für die Vorhersage des nächsten Zustands $Q$ nicht denselben DQN. Wir verwenden eine ältere Version davon, die im Code target_model heißt (statt model als Haupt-DQN). Dank dessen haben wir ein stabiles Ziel. Wir aktualisieren target_model , indem wir es so einstellen, dass alle 1000 Schritte Gewichtungen model werden. Aber model aktualisiert jeden Schritt.

Schauen wir uns den Code an, der das DQN-Modell erstellt:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Erstens übernimmt die Funktion die Dimensionen des Aktions- und Beobachtungsraums aus der gegebenen OpenAI-Gym-Umgebung. Man muss zum Beispiel wissen, wie viele Ausgänge unser Netzwerk haben wird. Sie muss gleich der Anzahl der Aktionen sein. Aktionen sind One-Hot-codiert:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Also (zB) links ist [1, 0] und rechts ist [0, 1].

Wir können sehen, dass die Beobachtungen als Eingabe übergeben werden. Als zweite Eingabe übergeben wir außerdem action_mask . Warum? Bei der Berechnung von $Q(s,a)$ müssen wir den $Q$-Wert nur für eine gegebene Aktion kennen, nicht für alle. action_mask enthält 1 für die Aktionen, die wir an die DQN-Ausgabe übergeben möchten. Wenn action_mask für eine Aktion 0 hat, dann wird der entsprechende $Q$-Wert in der Ausgabe auf Null gesetzt. Das tut die filtered_output Schicht. Wenn wir alle $Q$-Werte wollen (für die Max-Berechnung), können wir einfach alle übergeben.

Der Code verwendet keras.layers.Dense , um eine vollständig verbundene Ebene zu definieren. Keras ist eine Python-Bibliothek für Abstraktion auf höherer Ebene auf TensorFlow. Unter der Haube erstellt Keras ein TensorFlow-Diagramm mit Verzerrungen, korrekter Gewichtsinitialisierung und anderen Dingen auf niedriger Ebene. Wir hätten einfach rohes TensorFlow verwenden können, um das Diagramm zu definieren, aber es wird kein Einzeiler sein.

So werden Beobachtungen mit ReLU-Aktivierungen (rektifizierte lineare Einheit) an die erste verborgene Schicht weitergegeben. ReLU(x) ist nur eine $\textrm{max}(0, x)$ Funktion. Diese Ebene ist vollständig mit einer zweiten identischen Ebene verbunden, hidden_2 . Die Ausgabeschicht reduziert die Anzahl der Neuronen auf die Anzahl der Aktionen. Am Ende haben wir filtered_output , was die Ausgabe einfach mit action_mask .

Um $θ$-Gewichte zu finden, verwenden wir einen Optimierer namens „Adam“ mit einem mittleren quadratischen Fehlerverlust.

Mit einem Modell können wir es verwenden, um $Q$-Werte für gegebene Zustandsbeobachtungen vorherzusagen:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Wir wollen $Q$-Werte für alle Aktionen, also ist action_mask ein Vektor von Einsen.

Um das eigentliche Training durchzuführen, verwenden wir fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Batch enthält BATCH_SIZE Erlebnisse. next_q_values ​​ist $Q(s, a)$. q_values ​​ist $r + γ \space \textrm{max}_{a'}Q(s', a')$ aus der Bellman-Gleichung. Die von uns durchgeführten Aktionen sind einmal codiert und werden beim Aufrufen model.fit() als action_mask an die Eingabe übergeben. $y$ ist ein gebräuchlicher Buchstabe für ein „Ziel“ beim überwachten Lernen. Hier übergeben wir die q_values ​​. Ich mache q_values[:. None] q_values[:. None] , um die Array-Dimension zu erhöhen, da sie der Dimension des one_hot_actions Arrays entsprechen muss. Dies wird Slice-Notation genannt, wenn Sie mehr darüber lesen möchten.

Wir geben den Verlust zurück, um ihn in der TensorBoard-Protokolldatei zu speichern und später zu visualisieren. Es gibt noch viele andere Dinge, die wir überwachen werden: wie viele Schritte wir pro Sekunde machen, die gesamte RAM-Nutzung, wie hoch die durchschnittliche Episodenrückgabe ist usw. Sehen wir uns diese Diagramme an.

Laufen

Um die TensorBoard-Protokolldatei zu visualisieren, benötigen wir zunächst eine. Lassen Sie uns also einfach das Training durchführen:

 python run.py

Dadurch wird zunächst die Zusammenfassung unseres Modells gedruckt. Dann wird ein Protokollverzeichnis mit dem aktuellen Datum erstellt und das Training gestartet. Alle 2000 Schritte wird eine Protokollzeile ähnlich der folgenden gedruckt:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Alle 20.000 werden wir unser Modell anhand von 10.000 Schritten bewerten:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Nach 677 Episoden und 120.000 Schritten verbesserte sich der durchschnittliche Episodenrücklauf von -200 auf -136,75! Lernen ist es auf jeden Fall. Was avg_max_q_value ist, überlasse ich dem Leser als gute Übung. Aber es ist eine sehr nützliche Statistik, die man sich während des Trainings ansehen sollte.

Nach 200.000 Schritten ist unser Training beendet. Auf meiner Vierkern-CPU dauert es ungefähr 20 Minuten. Wir können in das date-log Verzeichnis schauen, zB 06-07-18-39-log . Es gibt vier Modelldateien mit der Erweiterung .h5 . Dies ist eine Momentaufnahme der TensorFlow-Diagrammgewichte, wir speichern sie alle 50.000 Schritte, um später einen Blick auf die gelernte Richtlinie zu werfen. So zeigen Sie es an:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Um die anderen möglichen Flags zu sehen: python run.py --help .

Jetzt erreicht das Auto das gewünschte Ziel viel besser. Im date-log Verzeichnis befindet sich auch die Datei events.out.* . Dies ist die Datei, in der TensorBoard seine Daten speichert. Wir schreiben mit dem einfachsten TensorBoardLogger , der in loggers.py. Um die Ereignisdatei anzuzeigen, müssen wir den lokalen TensorBoard-Server ausführen:

 tensorboard --logdir=.

--logdir nur auf das Verzeichnis, in dem sich Datumsprotokollverzeichnisse befinden, in unserem Fall ist dies das aktuelle Verzeichnis, also . . TensorBoard gibt die URL aus, auf der es lauscht. Wenn Sie http://127.0.0.1:6006 öffnen, sollten Sie acht Diagramme sehen, die diesen ähneln:

Einpacken

train() führt das gesamte Training durch. Wir erstellen zuerst das Modell und geben den Puffer wieder. Dann interagieren wir in einer Schleife, die der von see.py sehr ähnlich ist, mit der Umgebung und speichern Erfahrungen im Puffer. Wichtig ist, dass wir eine epsilon-gierige Politik verfolgen. Wir könnten immer die beste Aktion gemäß der $Q$-Funktion auswählen; Dies entmutigt jedoch die Erkundung, was die Gesamtleistung beeinträchtigt. Um die Exploration mit Epsilon-Wahrscheinlichkeit zu erzwingen, führen wir also zufällige Aktionen aus:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon wurde auf 1 % gesetzt. Nach 2000 Erfahrungen füllt sich das Replay genug, um mit dem Training zu beginnen. Wir tun dies, indem fit_batch() mit einem zufälligen Stapel von Erfahrungen aufrufen, die aus dem Wiedergabepuffer entnommen wurden:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Alle 20.000 Schritte werten wir die Ergebnisse aus und protokollieren sie (Auswertung erfolgt mit epsilon = 0 , total greedy policy):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

Der gesamte Code umfasst etwa 300 Zeilen, und run.py enthält etwa 250 der wichtigsten.

Man kann feststellen, dass es viele Hyperparameter gibt:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Und das sind noch lange nicht alle. Es gibt auch eine Netzwerkarchitektur – wir haben zwei versteckte Schichten mit 32 Neuronen, ReLU-Aktivierungen und Adam-Optimierer verwendet, aber es gibt viele andere Optionen. Schon kleine Veränderungen können einen großen Einfluss auf das Training haben. Es kann viel Zeit damit verbracht werden, Hyperparameter abzustimmen. In einem kürzlich durchgeführten OpenAI-Wettbewerb fand ein Zweitplatzierter heraus, dass es möglich ist, Rainbows Punktzahl nach Hyperparameter-Tuning fast zu verdoppeln . Natürlich muss man bedenken, dass es leicht ist, sich zu überanpassen. Derzeit kämpfen Verstärkungsalgorithmen mit dem Wissenstransfer in ähnliche Umgebungen. Unser Mountain Car ist derzeit nicht für alle Arten von Bergen verallgemeinerbar. Sie können die OpenAI Gym-Umgebung tatsächlich modifizieren und sehen, wie weit der Agent generalisieren kann.

Eine andere Übung besteht darin, einen besseren Satz von Hyperparametern als meinen zu finden. Es ist definitiv möglich. Ein Trainingslauf wird jedoch nicht ausreichen, um zu beurteilen, ob Ihre Veränderung eine Verbesserung darstellt. Normalerweise gibt es einen großen Unterschied zwischen den Trainingsläufen; die Varianz ist groß. Sie würden viele Läufe benötigen, um festzustellen, dass etwas besser ist. Wenn Sie mehr über ein so wichtiges Thema wie Reproduzierbarkeit lesen möchten, empfehle ich Ihnen, Deep Reinforcement Learning that Matters zu lesen. Anstatt von Hand abzustimmen, können wir diesen Prozess bis zu einem gewissen Grad automatisieren – wenn wir bereit sind, mehr Rechenleistung für das Problem aufzuwenden. Ein einfacher Ansatz besteht darin, einen vielversprechenden Wertebereich für einige Hyperparameter vorzubereiten und dann eine Gittersuche (Prüfung ihrer Kombinationen) durchzuführen, wobei die Trainings parallel laufen. Die Parallelisierung selbst ist ein großes Thema für sich, da sie für eine hohe Leistung entscheidend ist.

Deep $Q$-Learning stellt eine große Familie von Reinforcement-Learning-Algorithmen dar, die Wertiteration verwenden. Wir haben versucht, die $Q$-Funktion zu approximieren, und wir haben sie die meiste Zeit nur auf gierige Weise verwendet. Es gibt eine andere Familie, die Richtlinieniteration verwendet. Sie konzentrieren sich nicht darauf, die $Q$-Funktion zu approximieren, sondern direkt die optimale Strategie $π^*$ zu finden. Um zu sehen, wo die Werteiteration in die Landschaft der Reinforcement-Learning-Algorithmen passt:

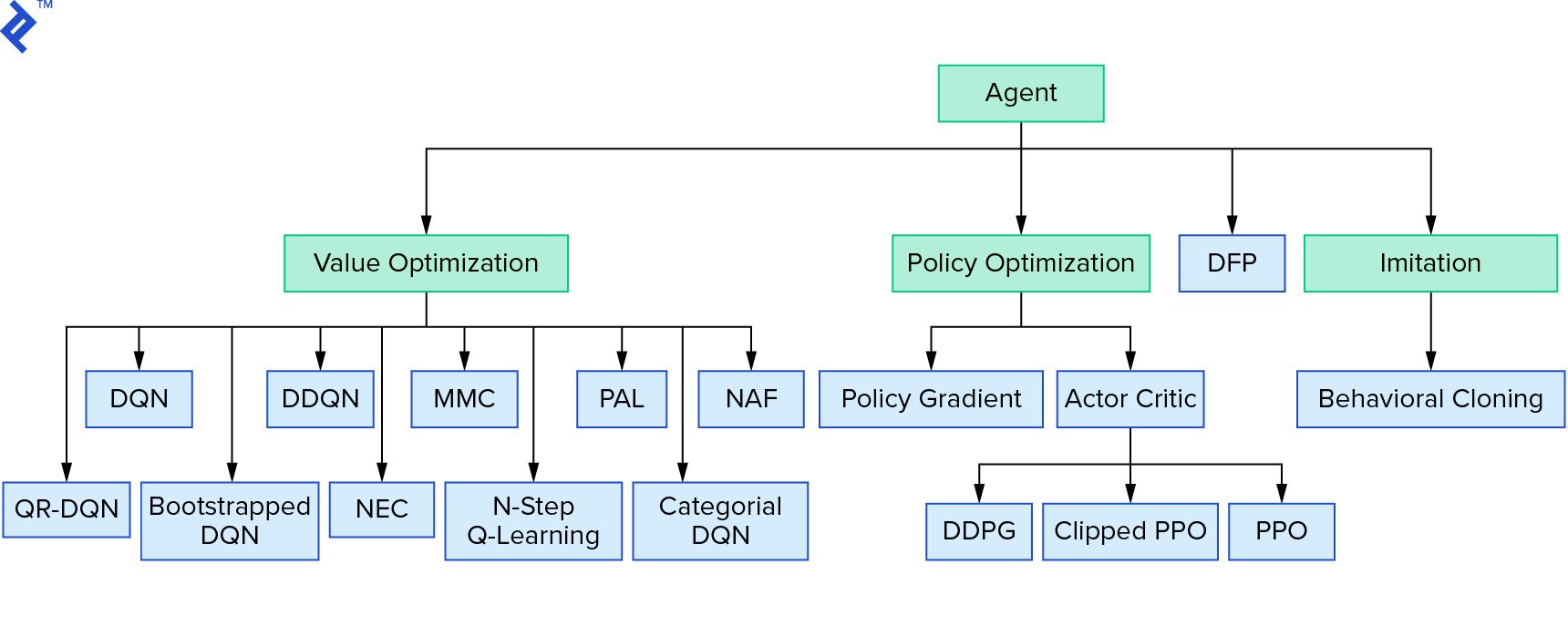
Ihre Gedanken könnten sein, dass Deep Reinforcement Learning spröde aussieht. Sie werden Recht haben; es gibt viele probleme. Sie können auf „Deep Reinforcement Learning Doesn’t Work Yet“ verweisen und „Reinforcement Learning hat nie funktioniert“, und „deep“ hat nur ein bisschen geholfen.

Damit ist das Tutorial abgeschlossen. Wir haben unseren eigenen Basis-DQN zu Lernzwecken implementiert. Sehr ähnlicher Code kann verwendet werden, um in einigen Atari-Spielen eine gute Leistung zu erzielen. In der Praxis nimmt man oft erprobte, performante Implementierungen, z. B. eine von OpenAI-Baselines. Wenn Sie sehen möchten, welchen Herausforderungen man begegnen kann, wenn man versucht, Deep Reinforcement Learning in einer komplexeren Umgebung anzuwenden, lesen Sie Unser NIPS 2017: Learning to Run-Ansatz. Wenn Sie in einer unterhaltsamen Wettbewerbsumgebung mehr erfahren möchten, werfen Sie einen Blick auf NIPS 2018 Competitions oder crowdai.org.

Wenn Sie auf dem Weg sind, ein Experte für maschinelles Lernen zu werden und Ihr Wissen über überwachtes Lernen vertiefen möchten, sehen Sie sich Videoanalyse zum maschinellen Lernen: Fische identifizieren an, um ein unterhaltsames Experiment zum Identifizieren von Fischen zu erhalten.