Глубокое погружение в обучение с подкреплением
Опубликовано: 2022-03-11Давайте углубимся в обучение с подкреплением. В этой статье мы рассмотрим конкретную проблему с современными библиотеками, такими как TensorFlow, TensorBoard, Keras и OpenAI gym. Вы увидите, как реализовать один из фундаментальных алгоритмов, называемый глубоким $Q$-обучением, чтобы изучить его внутреннюю работу. Что касается аппаратного обеспечения, то весь код будет работать на обычном ПК и использовать все найденные ядра ЦП (это обрабатывается TensorFlow из коробки).
Задача называется Mountain Car: Автомобиль находится на одномерной трассе, расположенной между двумя горами. Цель состоит в том, чтобы подняться на гору справа (достигнув флага). Однако двигатель автомобиля недостаточно силен, чтобы подняться на гору за один проход. Таким образом, единственный способ добиться успеха — это ездить туда-сюда, чтобы набрать обороты.
Эта задача была выбрана потому, что она достаточно проста, чтобы найти решение с обучением с подкреплением за считанные минуты на одном ядре ЦП. Однако он достаточно сложен, чтобы быть хорошим представителем.
Во-первых, я дам краткий обзор того, что делает обучение с подкреплением в целом. Затем мы рассмотрим основные термины и сформулируем с их помощью нашу проблему. После этого я опишу алгоритм глубокого $Q$-обучения и мы реализуем его для решения задачи.
Основы обучения с подкреплением
Обучение с подкреплением простыми словами — это обучение методом проб и ошибок. Главного героя называют «агентом», который в нашей задаче будет машиной. Агент совершает действие в среде и получает новое наблюдение и вознаграждение за это действие. Действия, ведущие к большему вознаграждению, усиливаются, отсюда и название. Как и многие другие вещи в области компьютерных наук, этот также был вдохновлен наблюдением за живыми существами.
Взаимодействие агента со средой представлено на следующем графике:
Агент получает наблюдение и вознаграждение за выполненное действие. Затем он выполняет еще одно действие и переходит на второй шаг. Окружающая среда теперь возвращает (вероятно) немного другое наблюдение и награду. Это продолжается до тех пор, пока не будет достигнуто конечное состояние, о чем сигнализируется отправкой агенту «done». Вся последовательность наблюдений > действий > следующих_наблюдений > награды называется эпизодом (или траекторией).
Возвращаясь к нашей горной машине: наша машина — агент. Окружающая среда представляет собой мир черного ящика одномерных гор. Действие автомобиля сводится только к одному числу: если оно положительное, двигатель толкает автомобиль вправо. Если отрицательный, он толкает машину влево. Агент воспринимает окружающую среду через наблюдение: положение автомобиля по оси X и скорость. Если мы хотим, чтобы наша машина ехала по вершине горы, мы определяем награду удобным способом: агент получает -1 к своей награде за каждый шаг, на котором он не достиг цели. Когда он достигает цели, эпизод заканчивается. Так что, по сути, агент наказывается за то, что он не находится в том положении, в котором мы хотим его видеть. Чем быстрее он ее достигнет, тем лучше для него. Цель агента — максимизировать общее вознаграждение, представляющее собой сумму вознаграждений за один эпизод. Таким образом, если он достигает нужной точки после, например, 110 шагов, он получает общий возврат -110, что было бы отличным результатом для Mountain Car, потому что, если он не достигает цели, он наказывается на 200 шагов. (отсюда и возврат -200).
Вот и вся формулировка проблемы. Теперь мы можем дать это алгоритмам, которые уже достаточно мощны, чтобы решать такие задачи за считанные минуты (если они хорошо настроены). Стоит отметить, что мы не говорим агенту, как достичь цели. Мы даже не даем никаких подсказок (эвристик). Агент сам найдет способ (политику) победить.
Настройка среды
Сначала скопируйте весь код учебника на свой диск:
git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorialТеперь нам нужно установить пакеты Python, которые мы будем использовать. Чтобы не устанавливать их в вашем пользовательском пространстве (и рисковать коллизиями), мы сделаем его чистым и установим их в среде conda. Если у вас не установлена conda, перейдите по ссылке https://conda.io/docs/user-guide/install/index.html.
Чтобы создать нашу среду conda:
conda create -n tutorial python=3.6.5 -yЧтобы активировать его:
source activate tutorial Вы должны увидеть (tutorial) рядом с приглашением в оболочке. Это означает, что среда conda с названием «tutorial» активна. С этого момента все команды должны выполняться в этой среде conda.
Теперь мы можем установить все зависимости в нашей герметичной среде conda:
pip install -r requirements.txtМы закончили установку, поэтому давайте запустим код. Нам не нужно самим реализовывать среду Mountain Car; библиотека OpenAI Gym предоставляет такую реализацию. Давайте посмотрим на случайного агента (агента, который выполняет случайные действия) в нашей среде:
import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render() Это файл see.py ; чтобы запустить его, выполните:
python see.pyВы должны увидеть, как машина беспорядочно движется вперед и назад. Каждый эпизод будет состоять из 200 шагов; общий доход будет -200.
Теперь нам нужно заменить случайные действия на что-то лучшее. Есть много алгоритмов, которые можно было бы использовать. Для вводного урока я думаю, что подход, называемый глубоким $Q$-обучением, хорошо подходит. Понимание этого метода дает прочную основу для изучения других подходов.
Глубокое $Q$-обучение
Алгоритм, который мы будем использовать, был впервые описан в 2013 году Mnih et al. в «Игре в Atari с глубоким обучением с подкреплением» и два года спустя отполирован в «Управление на уровне человека с помощью глубокого обучения с подкреплением». Многие другие работы основаны на этих результатах, в том числе текущий современный алгоритм Rainbow (2017):
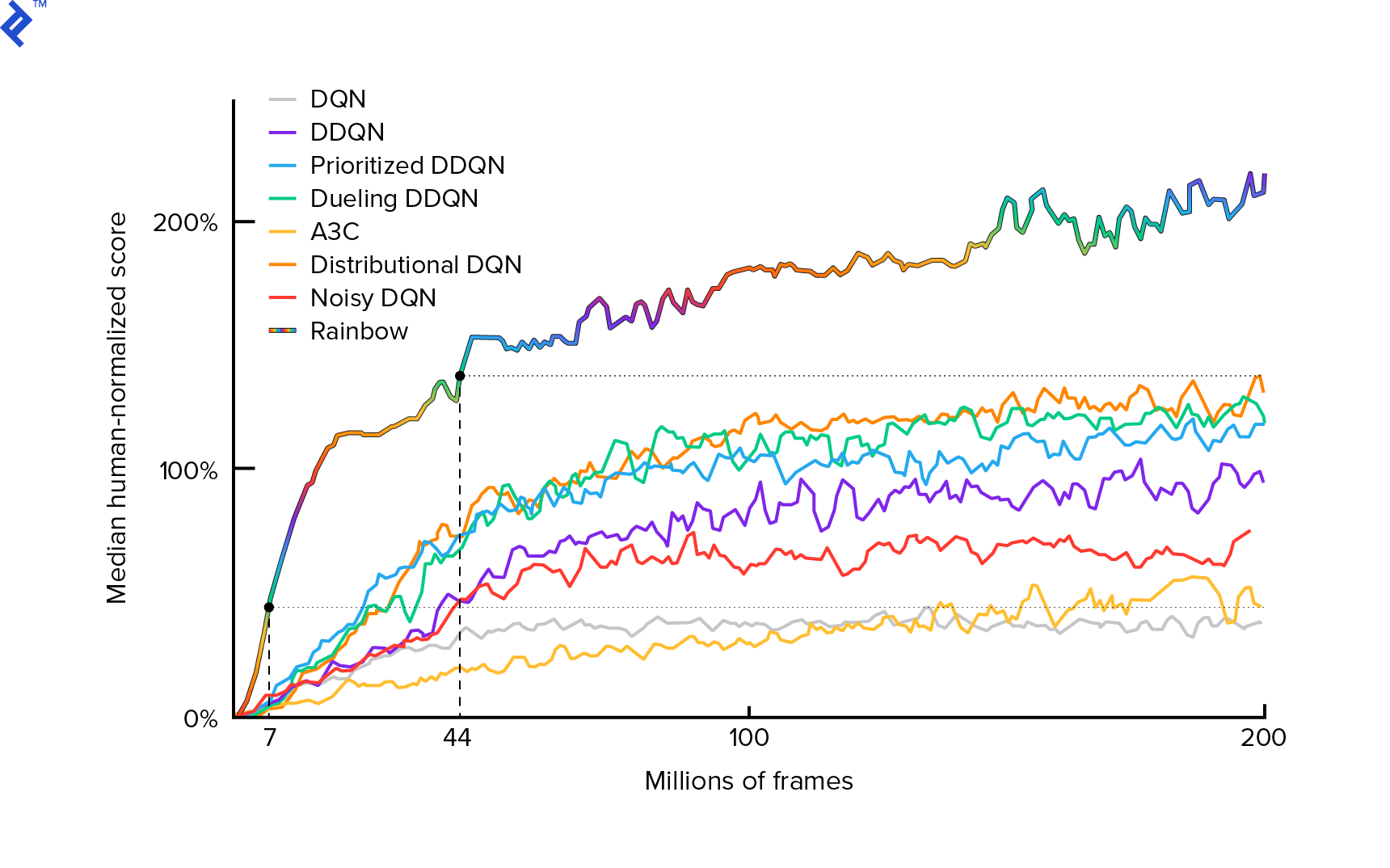
Rainbow достигает сверхчеловеческой производительности во многих играх для Atari 2600. Мы сосредоточимся на базовой версии DQN с как можно меньшим числом дополнительных улучшений, чтобы объем этого руководства был разумным.
Политика, обычно обозначаемая как $π(s)$, представляет собой функцию, возвращающую вероятности совершения отдельных действий в заданном состоянии $s$. Так, например, случайная политика Mountain Car возвращает для любого состояния: 50% слева, 50% справа. Во время игры мы делаем выборку из этой политики (дистрибутива), чтобы получить реальные действия.
$Q$-обучение (Q означает «Качество») относится к функции «действие-ценность», обозначаемой $Q_π(s, a)$. Он возвращает общий доход от заданного состояния $s$, выбирая действие $a$, следуя конкретной политике $π$. Общая отдача — это сумма всех наград в одном эпизоде (траектории).
Если бы мы знали оптимальную $Q$-функцию, обозначаемую $Q^*$, мы могли бы легко решить эту игру. Мы просто следили бы за действиями с наивысшим значением $Q^*$, т. е. с наивысшим ожидаемым доходом. Это гарантирует, что мы достигнем максимально возможной отдачи.
Однако часто мы не знаем $Q^*$. В таких случаях мы можем аппроксимировать — или «узнать» — это из взаимодействия с окружающей средой. Это часть названия «$Q$-обучение». В нем также есть слово «глубокий», потому что для аппроксимации этой функции мы будем использовать глубокие нейронные сети, которые являются универсальными аппроксиматорами функций. Глубокие нейронные сети, аппроксимирующие значения $Q$, получили название Deep Q-Networks (DQN). В простых средах (с количеством состояний, умещающимся в памяти) можно было бы просто использовать таблицу вместо нейронной сети для представления $Q$-функции, и в этом случае ее назвали бы «табличным $Q$-обучением».
Итак, наша цель сейчас — аппроксимировать функцию $Q^*$. Воспользуемся уравнением Беллмана:
\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]$s'$ — это состояние после $s$. $γ$ (гамма), обычно 0,99, является коэффициентом дисконтирования (это гиперпараметр). Это придает меньшее значение будущим вознаграждениям (поскольку они менее надежны, чем немедленные вознаграждения с нашим несовершенным $Q$). Уравнение Беллмана занимает центральное место в глубоком $Q$-обучении. В нем говорится, что значение $Q$ для данного состояния и действия равно вознаграждению $r$, полученному после выполнения действия $a$, плюс максимальное значение $Q$ для состояния, в котором мы находимся в $s'$. Самый высокий в том смысле, что мы выбираем действие $a'$, которое приводит к наибольшему общему доходу от $s'$.
С помощью уравнения Беллмана мы можем использовать обучение с учителем для аппроксимации $Q^*$. $Q$-функция будет представлена (параметризована) весами нейронной сети, обозначенными как $θ$ (тета). Простая реализация будет принимать состояние и действие в качестве входных данных сети и выводить Q-значение. Неэффективность заключается в том, что если мы хотим знать $Q$-значения для всех действий в заданном состоянии, нам нужно вызывать $Q$ столько раз, сколько существует действий. Есть гораздо лучший способ: брать на вход только состояние и выводить $Q$-значения для всех возможных действий. Благодаря этому мы можем получить $Q$-значения для всех действий всего за один прямой проход.
Начнем обучение сети $Q$ со случайными весами. Из окружающей среды мы получаем множество переходов (или «опытов»). Это кортежи (состояние, действие, следующее состояние, вознаграждение) или, короче, ($s$, $a$, $s'$, $r$). Мы храним тысячи из них в кольцевом буфере, который называется «воспроизведение опыта». Затем мы извлекаем опыт из этого буфера с желанием, чтобы уравнение Беллмана для него выполнялось. Мы могли бы пропустить буфер и применять опыт один за другим (это называется «онлайн» или «согласно политике»); проблема в том, что последующие события сильно коррелируют друг с другом, и когда это происходит, DQN плохо обучается. Вот почему было введено воспроизведение опыта («автономный», «неполитический» подход), чтобы выявить эту корреляцию данных. Код нашей простейшей реализации кольцевого буфера можно найти в файле replay_buffer.py , я рекомендую вам прочитать его.
Вначале, поскольку веса нашей нейронной сети были случайными, значение левой части уравнения Беллмана будет далеко от правой части. Квадрат разницы будет нашей функцией потерь. Будем минимизировать функцию потерь, изменив веса нейронной сети $θ$. Запишем нашу функцию потерь:
\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]Это переписанное уравнение Беллмана. Допустим, мы взяли опыт ($s$, слева, $s'$, -1) из воспроизведения опыта Mountain Car. Мы выполняем прямой проход через нашу сеть $Q$ с состоянием $s$, и для действия влево это дает нам, например, -120. Итак, $Q(s, \textrm{left}) = -120$. Затем мы передаем $s'$ в сеть, что дает нам, например, -130 для левого и -122 для правого. Таким образом, очевидно, что наилучшее действие для $s'$ является правильным, поэтому $\textrm{max}_{a'}Q(s', a') = -122$. Мы знаем $r$, это реальная награда, которая была -1. Таким образом, наш прогноз для сети $Q$ оказался немного неверным, потому что $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Таким образом, мы распространяем ошибку назад и слегка корректируем веса $θ$. Если бы мы снова рассчитали потери для того же опыта, они были бы ниже.
Одно важное замечание, прежде чем мы перейдем к коду. Заметим, что для обновления нашего DQN мы выполним два прохода вперед по самому DQN. Это часто приводит к нестабильному обучению. Чтобы облегчить это, для предсказания следующего состояния $Q$ мы не используем одно и то же DQN. Мы используем его более старую версию, которая в коде называется target_model (вместо model , являющейся основным DQN). Благодаря этому у нас есть стабильная цель. Мы обновляем target_model , устанавливая вес model каждые 1000 шагов. Но model обновляется каждый шаг.
Давайте посмотрим на код, создающий модель DQN:
def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return modelВо-первых, функция берет размеры пространства действия и наблюдения из заданной среды OpenAI Gym. Нужно знать, например, сколько выходов будет у нашей сети. Оно должно быть равно количеству действий. Действия являются одним горячим кодированием:

def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hotТаким образом, (например) слева будет [1, 0], а справа будет [0, 1].
Мы видим, что наблюдения передаются в качестве входных данных. Мы также передаем action_mask в качестве второго входа. Почему? При вычислении $Q(s,a)$ нам нужно знать значение $Q$ только для одного заданного действия, а не для всех. action_mask содержит 1 для действий, которые мы хотим передать на выход DQN. Если action_mask имеет 0 для какого-то действия, то соответствующее значение $Q$ на выходе будет обнулено. Это делает слой filtered_output . Если нам нужны все значения $Q$ (для максимального расчета), мы можем просто передать их все.
Код использует keras.layers.Dense для определения полносвязного слоя. Keras — это библиотека Python для высокоуровневой абстракции поверх TensorFlow. Под капотом Keras создает график TensorFlow со смещениями, правильной инициализацией веса и другими низкоуровневыми вещами. Мы могли бы просто использовать необработанный TensorFlow для определения графика, но это не будет однострочным.
Таким образом, наблюдения передаются на первый скрытый слой с активацией ReLU (выпрямленная линейная единица). ReLU(x) — это просто функция $\textrm{max}(0, x)$. Этот слой полностью связан со вторым идентичным hidden_2 . Выходной слой сводит количество нейронов к количеству действий. В итоге у нас есть filtered_output , который просто умножает вывод на action_mask .
Чтобы найти веса $θ$, мы будем использовать оптимизатор под названием «Адам» с потерей среднеквадратичной ошибки.
Имея модель, мы можем использовать ее для прогнозирования значений $Q$ для данных наблюдений за состоянием:
def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask]) Нам нужны $Q$-значения для всех действий, поэтому action_mask представляет собой вектор из единиц.
Для фактического обучения мы будем использовать fit_batch() :
def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0] Пакет содержит BATCH_SIZE . next_q_values равно $Q(s, a)$. q_values равно $r + γ \space \textrm{max}_{a'}Q(s', a')$ из уравнения Беллмана. Действия, которые мы предприняли, являются одним горячим кодированием и передаются как action_mask на вход при вызове model.fit() . $y$ — это обычная буква для «цели» в обучении с учителем. Здесь мы q_values . Я делаю q_values[:. None] q_values[:. None] , чтобы увеличить размер массива, поскольку он должен соответствовать размеру массива one_hot_actions . Это называется нотацией среза, если вы хотите узнать об этом подробнее.
Мы возвращаем потерю, чтобы сохранить ее в файле журнала TensorBoard и позже визуализировать. Есть много других вещей, которые мы будем отслеживать: сколько шагов в секунду мы делаем, общее использование оперативной памяти, каков средний возврат эпизода и т. д. Давайте посмотрим на эти графики.
Бег
Чтобы визуализировать файл журнала TensorBoard, нам сначала нужно его иметь. Итак, давайте просто запустим обучение:
python run.pyЭто сначала напечатает сводку нашей модели. Затем он создаст каталог журнала с текущей датой и начнет обучение. Каждые 2000 шагов будет печататься логлайн, подобный этому:
episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAMКаждые 20 000 мы будем оценивать нашу модель на 10 000 шагов:
Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004 После 677 эпизодов и 120 000 шагов средний возврат эпизода улучшился с -200 до -136,75! Это определенно обучение. Что такое avg_max_q_value , я оставляю читателю в качестве хорошего упражнения. Но это очень полезная статистика для просмотра во время тренировки.
После 200 000 шагов наша тренировка завершена. На моем четырехъядерном процессоре это занимает около 20 минут. Мы можем заглянуть внутрь каталога date-log , например, 06-07-18-39-log . Будет четыре файла модели с расширением .h5 . Это моментальный снимок весов графика TensorFlow, мы сохраняем их каждые 50 000 шагов, чтобы позже взглянуть на политику, которую мы изучили. Чтобы просмотреть его:
python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view Чтобы увидеть другие возможные флаги: python run.py --help .
Теперь машина намного лучше справляется с достижением желаемой цели. В каталоге date-log также находится файл events.out.* . Это файл, в котором TensorBoard хранит свои данные. Пишем в него с помощью простейшего TensorBoardLogger определенного в loggers.py. Чтобы просмотреть файл событий, нам нужно запустить локальный сервер TensorBoard:
tensorboard --logdir=. --logdir просто указывает на каталог, в котором есть каталоги журнала даты, в нашем случае это будет текущий каталог, поэтому . . TensorBoard печатает URL-адрес, по которому он прослушивает. Если вы откроете http://127.0.0.1:6006, вы должны увидеть восемь графиков, похожих на эти:
Подведение итогов
train() выполняет все обучение. Сначала мы создаем модель и воспроизводим буфер. Затем в цикле, очень похожем на цикл из see.py , мы взаимодействуем с окружением и сохраняем опыт в буфере. Важно то, что мы следуем эпсилон-жадной политике. Мы всегда могли выбрать наилучшее действие по $Q$-функции; однако это препятствует исследованию, что вредит общей производительности. Таким образом, чтобы обеспечить исследование с эпсилон-вероятностью, мы выполняем случайные действия:
def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action Эпсилон был установлен на 1%. После 2000 опытов повтор заполняется достаточно, чтобы начать тренировку. Мы делаем это, вызывая fit_batch() со случайным набором опытов, выбранных из буфера воспроизведения:
batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch) Каждые 20 000 шагов мы оцениваем и регистрируем результаты (оценка выполняется с epsilon = 0 , полностью жадная политика):
if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step) Весь код составляет около 300 строк, а run.py содержит около 250 наиболее важных из них.
Можно заметить, что есть много гиперпараметров:
DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000И это даже не все из них. Есть и сетевая архитектура — мы использовали два скрытых слоя с 32 нейронами, активации ReLU и оптимизатор Adam, но есть масса других вариантов. Даже небольшие изменения могут оказать огромное влияние на тренировку. Много времени можно потратить на настройку гиперпараметров. В недавнем соревновании OpenAI участник, занявший второе место, обнаружил, что можно почти удвоить результат Rainbow после настройки гиперпараметров. Естественно, нужно помнить, что легко переобучиться. В настоящее время алгоритмы подкрепления борются с переносом знаний в аналогичные среды. Наш горный автомобиль сейчас не подходит для всех типов гор. На самом деле вы можете изменить среду OpenAI Gym и посмотреть, насколько далеко агент может обобщить.
Еще одним упражнением будет поиск лучшего набора гиперпараметров, чем мой. Это определенно возможно. Однако одного тренировочного прогона будет недостаточно, чтобы судить о том, является ли ваше изменение улучшением. Обычно между тренировочными забегами есть большая разница; разница большая. Вам потребуется много прогонов, чтобы определить, что что-то лучше. Если вы хотите узнать больше о такой важной теме, как воспроизводимость, я рекомендую вам прочитать Глубокое обучение с подкреплением, которое имеет значение. Вместо того, чтобы настраивать вручную, мы можем до некоторой степени автоматизировать этот процесс, если мы готовы потратить больше вычислительной мощности на решение проблемы. Простой подход состоит в том, чтобы подготовить перспективный диапазон значений для некоторых гиперпараметров, а затем запустить поиск по сетке (проверив их комбинации) с параллельным обучением. Распараллеливание само по себе является большой темой, так как имеет решающее значение для высокой производительности.
Глубокое $Q$-обучение представляет собой большое семейство алгоритмов обучения с подкреплением, которые используют итерацию значений. Мы пытались аппроксимировать $Q$-функцию, и большую часть времени использовали ее жадно. Существует еще одно семейство, в котором используется итерация политики. Они сосредоточены не на аппроксимации $Q$-функции, а на непосредственном поиске оптимальной политики $π^*$. Чтобы увидеть, как итерация значения вписывается в ландшафт алгоритмов обучения с подкреплением:
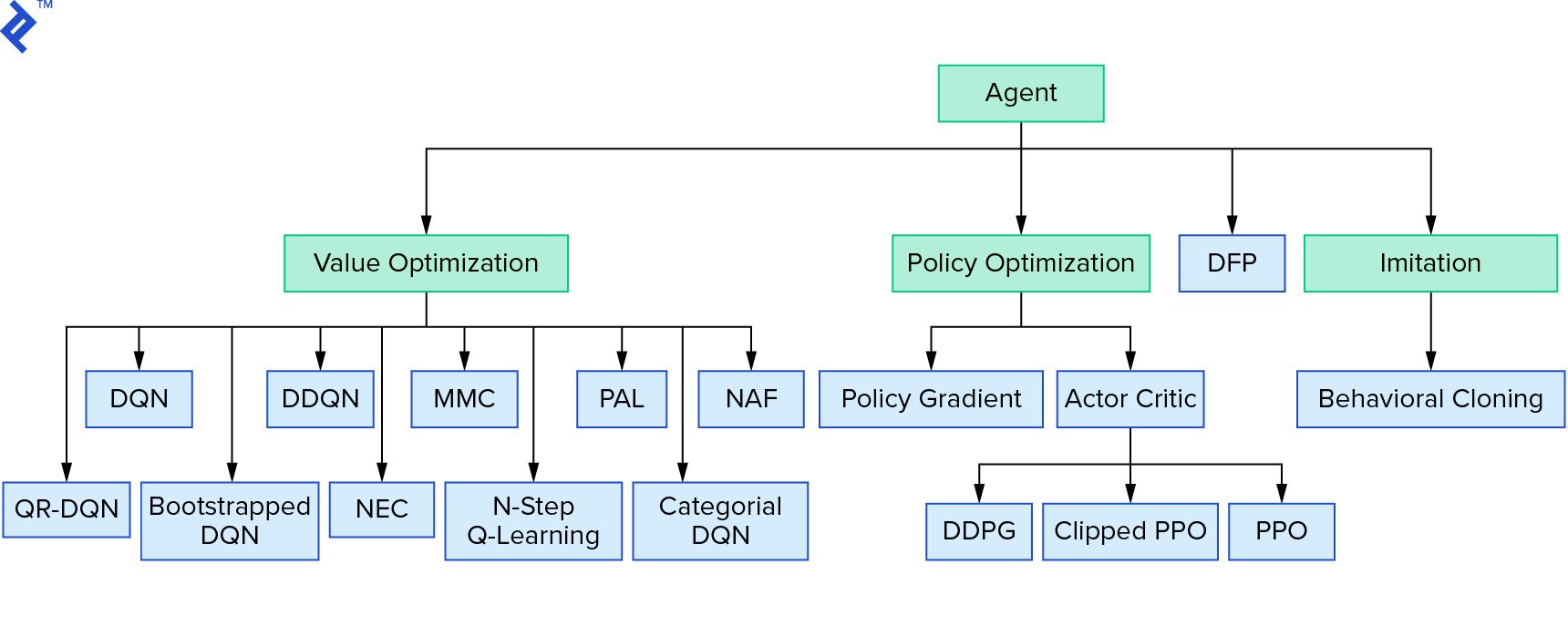
Возможно, вы думаете, что глубокое обучение с подкреплением выглядит хрупким. Вы будете правы; есть много проблем. Вы можете сослаться на «Глубокое обучение с подкреплением еще не работает» и «Обучение с подкреплением никогда не работало», а «глубокое» помогло лишь немного.
На этом урок заканчивается. Мы внедрили собственный базовый DQN для учебных целей. Очень похожий код можно использовать для достижения хорошей производительности в некоторых играх Atari. В практических приложениях часто берут проверенные высокопроизводительные реализации, например, одну из базовых линий OpenAI. Если вы хотите увидеть, с какими проблемами можно столкнуться при попытке применить глубокое обучение с подкреплением в более сложной среде, вы можете прочитать Наш NIPS 2017: подход Learning to Run. Если вы хотите узнать больше в веселой соревновательной среде, загляните на NIPS 2018 Competitions или на crowdai.org.
Если вы на пути к тому, чтобы стать экспертом в области машинного обучения и хотели бы углубить свои знания в области обучения с учителем, ознакомьтесь с видеоанализом машинного обучения: идентификация рыбы , чтобы провести занимательный эксперимент по идентификации рыбы.
