O scufundare profundă în învățarea prin întărire

Să aruncăm o adâncime în învățarea prin întărire. În acest articol, vom aborda o problemă concretă cu bibliotecile moderne, cum ar fi TensorFlow, TensorBoard, Keras și OpenAI gym. Veți vedea cum să implementați unul dintre algoritmii fundamentali numiti deep $Q$-learning pentru a învăța funcționarea sa interioară. În ceea ce privește hardware-ul, întregul cod va funcționa pe un computer obișnuit și va folosi toate nucleele CPU găsite (acesta este gestionat imediat de TensorFlow).

Problema se numește Mountain Car: O mașină se află pe o pistă unidimensională, poziționată între doi munți. Scopul este să urcăm muntele din dreapta (atingând steag). Cu toate acestea, motorul mașinii nu este suficient de puternic pentru a urca muntele într-o singură trecere. Prin urmare, singura modalitate de a reuși este să conduceți înainte și înapoi pentru a crea impuls.

Această problemă a fost aleasă deoarece este suficient de simplu pentru a găsi o soluție cu învățare prin consolidare în câteva minute pe un singur nucleu CPU. Cu toate acestea, este suficient de complex pentru a fi un bun reprezentant.

În primul rând, voi oferi un scurt rezumat a ceea ce face învățarea prin întărire în general. Apoi, vom acoperi termenii de bază și vom exprima problema noastră cu ei. După aceea, voi descrie algoritmul de învățare profundă $Q$ și îl vom implementa pentru a rezolva problema.

Elementele de bază ale învățării prin întărire

Învățarea prin întărire în cele mai simple cuvinte este învățarea prin încercare și eroare. Personajul principal este numit „agent”, care ar fi o mașină în problema noastră. Agentul face o acțiune într-un mediu și primește o nouă observație și o recompensă pentru acțiunea respectivă. Acțiunile care conduc la recompense mai mari sunt consolidate, de unde și numele. Ca și în cazul multor alte lucruri din informatică, și acesta a fost inspirat de observarea unor creaturi vii.

Interacțiunile agentului cu un mediu sunt rezumate în următorul grafic:

Agentul primește o observație și o recompensă pentru acțiunea efectuată. Apoi face o altă acțiune și trece la pasul doi. Mediul returnează acum o observație și o recompensă (probabil) ușor diferite. Aceasta continuă până când se ajunge la starea terminală, semnalată prin trimiterea „terminat” unui agent. Întreaga secvență de observații > acțiuni > următoarele_observații > recompense se numește episod (sau traiectorie).

Revenind la mașina noastră de munte: mașina noastră este un agent. Mediul este o lume cutie neagră de munți unidimensionali. Acțiunea mașinii se rezumă la un singur număr: dacă este pozitiv, motorul împinge mașina spre dreapta. Dacă este negativ, împinge mașina spre stânga. Agentul percepe un mediu printr-o observație: poziția X și viteza mașinii. Dacă dorim ca mașina noastră să circule pe vârful muntelui, definim recompensa într-un mod convenabil: agentul primește -1 la recompensa sa pentru fiecare pas în care nu a atins obiectivul. Când atinge scopul, episodul se termină. Deci, de fapt, agentul este pedepsit pentru că nu se află într-o poziție în care ne dorim să fie. Cu cât ajunge mai repede la el, cu atât mai bine pentru el. Scopul agentului este de a maximiza recompensa totală, care este suma recompenselor dintr-un episod. Deci dacă ajunge la punctul dorit după, de exemplu, 110 pași, primește un randament total de -110, ceea ce ar fi un rezultat grozav pentru Mountain Car, pentru că dacă nu atinge obiectivul, atunci se pedepsește cu 200 de pași. (prin urmare, un randament de -200).

Aceasta este formularea întregii probleme. Acum, o putem da algoritmilor, care sunt deja suficient de puternici pentru a rezolva astfel de probleme în câteva minute (dacă sunt bine reglați). Este de remarcat faptul că nu îi spunem agentului cum să atingă obiectivul. Nici măcar nu oferim indicii (euristice). Agentul va găsi o modalitate (o politică) de a câștiga singur.

Configurarea Mediului

Mai întâi, copiați întregul cod tutorial pe disc:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Acum, trebuie să instalăm pachetele Python pe care le vom folosi. Pentru a nu le instala în spațiul dvs. de utilizator (și riscați coliziuni), îl vom curăța și le vom instala în mediul conda. Dacă nu aveți conda instalat, vă rugăm să urmați https://conda.io/docs/user-guide/install/index.html.

Pentru a crea mediul nostru conda:

 conda create -n tutorial python=3.6.5 -y

Pentru a-l activa:

 source activate tutorial

Ar trebui să vedeți (tutorial) lângă promptul dvs. în shell. Înseamnă că un mediu conda cu numele „tutorial” este activ. De acum înainte, toate comenzile ar trebui să fie executate în acel mediu conda.

Acum, putem instala toate dependențele în mediul nostru ermetic conda:

 pip install -r requirements.txt

Am terminat cu instalarea, așa că hai să rulăm niște cod. Nu trebuie să implementăm noi înșine mediul Mountain Car; biblioteca OpenAI Gym oferă această implementare. Să vedem un agent aleatoriu (un agent care face acțiuni aleatorii) în mediul nostru:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Acesta este fișierul see.py ; pentru a-l rula, executa:

 python see.py

Ar trebui să vezi o mașină mergând la întâmplare înainte și înapoi. Fiecare episod va consta din 200 de pași; rentabilitatea totală va fi -200.

Acum trebuie să înlocuim acțiunile aleatorii cu ceva mai bun. Există mulți algoritmi pe care i-ar putea folosi. Pentru un tutorial introductiv, cred că o abordare numită deep $Q$-learning este potrivită. Înțelegerea acestei metode oferă o bază fermă pentru învățarea altor abordări.

Învățare profundă $Q$

Algoritmul pe care îl vom folosi a fost descris pentru prima dată în 2013 de Mnih et al. în Playing Atari with Deep Reinforcement Learning și șlefuit doi ani mai târziu în controlul la nivel uman prin învățare deep reinforcement. Multe alte lucrări sunt construite pe aceste rezultate, inclusiv algoritmul actual de ultimă generație Rainbow (2017):

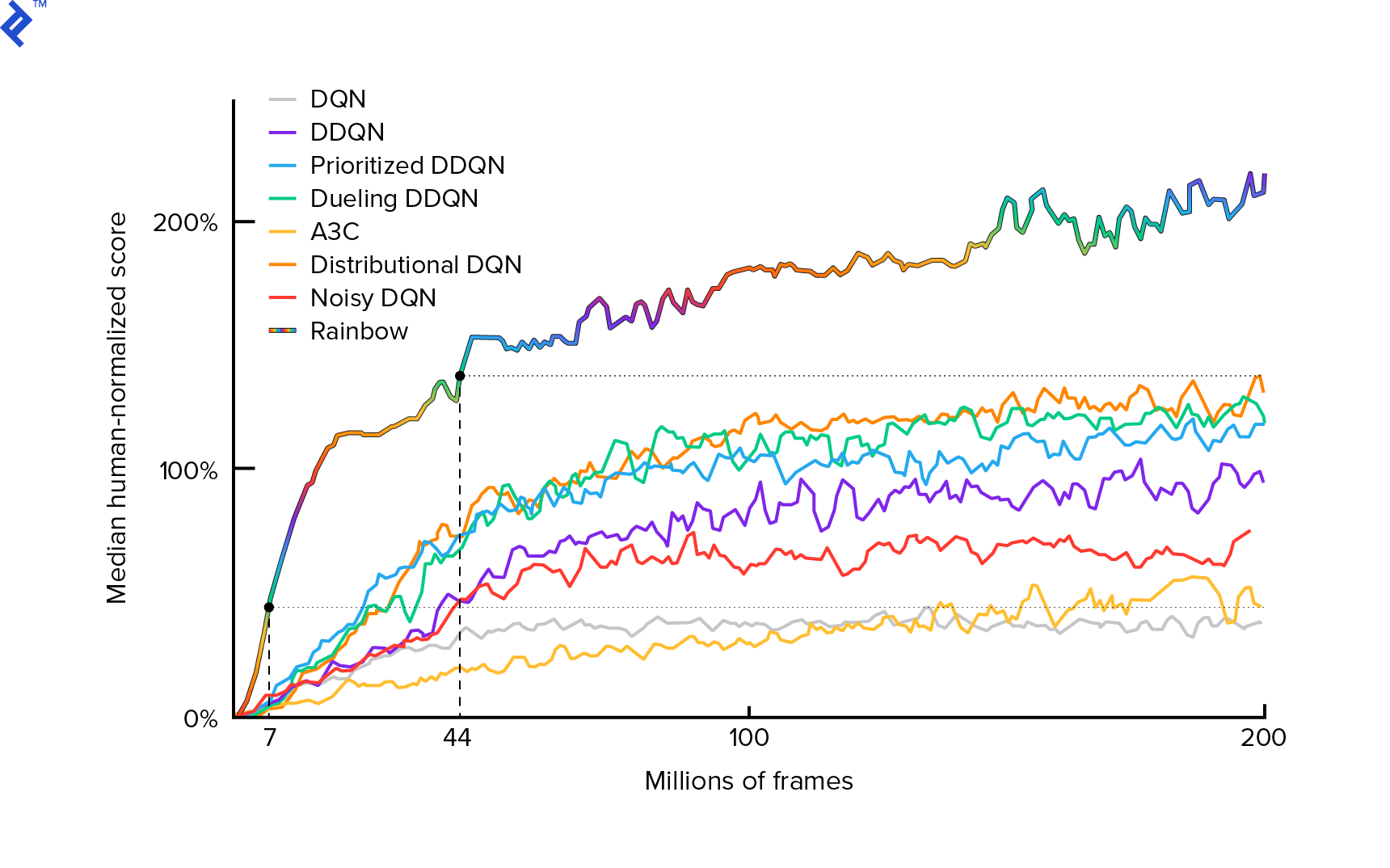
Rainbow atinge performanțe supraomenești la multe jocuri Atari 2600. Ne vom concentra pe versiunea de bază DQN, cu un număr cât mai mic de îmbunătățiri suplimentare posibil, pentru a menține acest tutorial la o dimensiune rezonabilă.

O politică, denumită de obicei $π(s)$, este o funcție care returnează probabilități de a întreprinde acțiuni individuale într-o stare dată $s$. Deci, de exemplu, o poliță Mountain Car aleatoare revine pentru orice stat: 50% stânga, 50% dreapta. În timpul jocului, eșantionăm din acea politică (distribuție) pentru a obține acțiuni reale.

$Q$-învățare (Q este pentru calitate) se referă la funcția acțiune-valoare notă $Q_π(s, a)$. Returnează randamentul total dintr-o stare dată $s$, alegând acțiunea $a$, urmând o politică concretă $π$. Rentabilitatea totală este suma tuturor recompenselor dintr-un episod (traiectorie).

Dacă am cunoaște funcția optimă $Q$, notată $Q^*$, am putea rezolva jocul cu ușurință. Am urma doar acțiunile cu cea mai mare valoare de $Q^*$, adică cea mai mare rentabilitate așteptată. Acest lucru garantează că vom atinge cel mai mare profit posibil.

Cu toate acestea, adesea nu știm $Q^*$. În astfel de cazuri, îl putem aproxima – sau „învăța” – din interacțiunile cu mediul. Aceasta este partea „$Q$-learning” din nume. Există, de asemenea, cuvântul „adânc” în el, deoarece, pentru a aproxima acea funcție, vom folosi rețele neuronale profunde, care sunt aproximatori de funcții universale. Rețelele neuronale profunde care aproximează valorile $Q$ au fost denumite Deep Q-Networks (DQN). În medii simple (cu numărul de stări care se potrivește în memorie), s-ar putea folosi doar un tabel în loc de o rețea neuronală pentru a reprezenta funcția $Q$, caz în care ar fi numită „învățare tabulară $Q$”.

Deci, scopul nostru acum este să aproximăm funcția $Q^*$. Vom folosi ecuația Bellman:

\[Q(s, a) = r + γ \space \textrm{max}_{a'} Q(s', a')\]

$s'$ este statul după $s$. $γ$ (gama), de obicei 0,99, este un factor de reducere (este un hiperparametru). Acordă o pondere mai mică recompenselor viitoare (pentru că sunt mai puțin sigure decât recompensele imediate cu $Q$-ul nostru imperfect). Ecuația Bellman este centrală pentru învățarea $Q$ profundă. Se spune că valoarea $Q$ pentru o anumită stare și acțiune este o recompensă $r$ primită după acțiunea $a$ plus cea mai mare valoare $Q$ pentru statul în care ajungem în $s'$. Cel mai mare este într-un sens că alegem o acțiune $a'$, care duce la cea mai mare rentabilitate totală de la $s'$.

Cu ecuația Bellman, putem folosi învățarea supravegheată pentru a aproxima $Q^*$. Funcția $Q$ va fi reprezentată (parametrizată) prin greutățile rețelei neuronale notate cu $θ$ (theta). O implementare simplă ar necesita o stare și o acțiune ca rețea de intrare și de ieșire a valorii Q. Ineficiența este că, dacă vrem să cunoaștem valorile $Q$ pentru toate acțiunile dintr-o stare dată, trebuie să apelăm $Q$ de câte ori există acțiuni. Există o modalitate mult mai bună: să luați doar starea ca intrare și valorile de ieșire $Q$ pentru toate acțiunile posibile. Datorită acesteia, putem obține valori $Q$ pentru toate acțiunile într-o singură trecere înainte.

Începem să antrenăm rețeaua $Q$ cu greutăți aleatorii. Din mediu, obținem multe tranziții (sau „experiențe”). Acestea sunt tuple ale lui (stare, acțiune, stare următoare, recompensă) sau, pe scurt, ($s$, $a$, $s'$, $r$). Stocăm mii de ele într-un buffer de apel numit „reluare experiență”. Apoi, eșantionăm experiențe din acel tampon cu dorința ca ecuația Bellman să le aibă. Am fi putut sări peste buffer și să aplicăm experiențele una câte una (acesta se numește „online” sau „on-policy”); problema este că experiențele ulterioare sunt foarte corelate între ele și DQN se antrenează prost atunci când se întâmplă acest lucru. De aceea a fost introdusă redarea experienței (o abordare „offline”, „în afara politicii”) pentru a dezvălui această corelație a datelor. Codul celei mai simple implementări a bufferului inel poate fi găsit în fișierul replay_buffer.py , vă încurajez să-l citiți.

La început, deoarece greutățile rețelei noastre neuronale erau aleatorii, valoarea din partea stângă a ecuației Bellman va fi departe de partea dreaptă. Diferența la pătrat va fi funcția noastră de pierdere. Vom minimiza funcția de pierdere prin modificarea greutăților rețelei neuronale $θ$. Să scriem funcția noastră de pierdere:

\[L(θ) = [Q(s, a) - r - γ \space \textrm{max}_{a'}Q(s', a')]^2\]

Este o ecuație Bellman rescrisă. Să presupunem că am testat o experiență ($s$, stânga, $s'$, -1) din reluarea experienței Mountain Car. Facem o trecere înainte prin rețeaua noastră $Q$ cu starea $s$ și pentru acțiunea rămasă ne dă -120, de exemplu. Deci, $Q(s, \textrm{stânga}) = -120$. Apoi alimentăm $s'$ în rețea, ceea ce ne oferă, de exemplu, -130 pentru stânga și -122 pentru dreapta. Deci, în mod clar, cea mai bună acțiune pentru $s'$ este corectă, deci $\textrm{max}_{a'}Q(s', a') = -122$. Știm $r$, aceasta este recompensa reală, care a fost -1. Deci predicția noastră de rețea $Q$ a fost ușor greșită, deoarece $L(θ) = [-120 - 1 + 0,99 ⋅ 122]^2 = (-0,22^2) = 0,0484$. Deci propagăm înapoi eroarea și corectăm ușor greutățile $θ$. Dacă ar fi să calculăm din nou pierderea pentru aceeași experiență, acum ar fi mai mică.

O observație importantă înainte de a trece la cod. Să observăm că, pentru a actualiza DQN-ul nostru, vom face două treceri înainte pe DQN... în sine. Acest lucru duce adesea la o învățare instabilă. Pentru a atenua acest lucru, pentru următoarea predicție a stării $Q$, nu folosim același DQN. Folosim o versiune mai veche a acesteia, care în cod se numește target_model (în loc de model , fiind DQN-ul principal). Datorită acestui fapt, avem o țintă stabilă. Actualizăm target_model setându-l să model greutăți la fiecare 1000 de pași. Dar model se actualizează la fiecare pas.

Să ne uităm la codul care creează modelul DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

În primul rând, funcția preia dimensiunile spațiului de acțiune și observație din mediul dat OpenAI Gym. Este necesar să știm, de exemplu, câte ieșiri va avea rețeaua noastră. Trebuie să fie egal cu numărul de acțiuni. Acțiunile sunt una la cald:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Deci (de exemplu) stânga va fi [1, 0] și dreapta va fi [0, 1].

Putem vedea că observațiile sunt transmise ca intrare. De asemenea, transmitem action_mask ca a doua intrare. De ce? Când calculăm $Q(s,a)$, trebuie să cunoaștem valoarea $Q$ numai pentru o acțiune dată, nu pentru toate. action_mask conține 1 pentru acțiunile pe care dorim să le transmitem la ieșirea DQN. Dacă action_mask are 0 pentru o anumită acțiune, atunci valoarea $Q$ corespunzătoare va fi zero pe rezultat. Stratul filtered_output face asta. Dacă vrem toate valorile $Q$ (pentru calculul maxim), le putem trece pe toate.

Codul folosește keras.layers.Dense pentru a defini un strat complet conectat. Keras este o bibliotecă Python pentru abstracție la nivel superior pe TensorFlow. Sub capotă, Keras creează un grafic TensorFlow, cu părtiniri, inițializare corectă a greutății și alte lucruri de nivel scăzut. Am fi putut folosi doar TensorFlow brut pentru a defini graficul, dar nu va fi o singură linie.

Deci, observațiile sunt transmise la primul strat ascuns, cu activări ReLU (unitate liniară rectificată). ReLU(x) este doar o funcție $\textrm{max}(0, x)$. Acest strat este complet conectat cu un al doilea identic, hidden_2 . Stratul de ieșire reduce numărul de neuroni la numărul de acțiuni. În cele din urmă, avem filtered_output , care doar înmulțește rezultatul cu action_mask .

Pentru a găsi ponderi $θ$, vom folosi un optimizator numit „Adam” cu o pierdere de eroare medie pătrată.

Având un model, îl putem folosi pentru a prezice valorile $Q$ pentru observațiile de stare date:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Dorim $Q$-valori pentru toate acțiunile, astfel action_mask este un vector al celor.

Pentru a face antrenamentul propriu-zis, vom folosi fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Lotul conține BATCH_SIZE experiențe. next_q_values ​​este $Q(s, a)$. q_values ​​este $r + γ \space \textrm{max}_{a'}Q(s', a')$ din ecuația Bellman. Acțiunile pe care le-am întreprins sunt unul codificat la cald și transmis ca action_mask la intrare când apelăm model.fit() . $y$ este o literă comună pentru o „țintă” în învățarea supravegheată. Aici trecem q_values ​​. Eu fac q_values[:. None] q_values[:. None] pentru a crește dimensiunea matricei, deoarece trebuie să corespundă dimensiunii matricei one_hot_actions . Aceasta se numește notație slice dacă doriți să citiți mai multe despre aceasta.

Returnăm pierderea pentru a o salva în fișierul jurnal TensorBoard și mai târziu a vizualiza. Sunt multe alte lucruri pe care le vom monitoriza: câți pași pe secundă facem, utilizarea totală a memoriei RAM, care este revenirea medie a episodului etc. Să vedem acele diagrame.

Alergare

Pentru a vizualiza fișierul jurnal TensorBoard, mai întâi trebuie să avem unul. Deci haideți doar să rulăm antrenamentul:

 python run.py

Acesta va imprima mai întâi rezumatul modelului nostru. Apoi va crea un director de jurnal cu data curentă și va începe antrenamentul. La fiecare 2000 de pași, se va tipări un jurnal similar cu acesta:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

La fiecare 20.000, vom evalua modelul nostru pe 10.000 de pași:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

După 677 de episoade și 120.000 de pași, revenirea medie a episodului sa îmbunătățit de la -200 la -136,75! Cu siguranță este învățat. Ce este avg_max_q_value îl las cititorului ca un exercițiu bun. Dar este o statistică foarte utilă pe care să o analizăm în timpul antrenamentului.

După 200.000 de pași, pregătirea noastră este terminată. Pe procesorul meu cu patru nuclee, durează aproximativ 20 de minute. Putem căuta în directorul date-log , de exemplu, 06-07-18-39-log . Vor exista patru fișiere model cu extensia .h5 . Acesta este un instantaneu al greutăților grafice TensorFlow, le salvăm la fiecare 50.000 de pași pentru a ne uita mai târziu la politica pe care am aflat-o. Pentru a o vizualiza:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Pentru a vedea celelalte semnale posibile: python run.py --help .

Acum, mașina face o treabă mult mai bună pentru a atinge scopul dorit. În directorul date-log , există și fișierul events.out.* . Acesta este fișierul în care TensorBoard își stochează datele. Îi scriem folosind cel mai simplu TensorBoardLogger definit în loggers.py. Pentru a vizualiza fișierul de evenimente, trebuie să rulăm serverul local TensorBoard:

 tensorboard --logdir=.

--logdir indică doar directorul în care există directoare de jurnal de date, în cazul nostru, acesta va fi directorul curent, deci . . TensorBoard tipărește adresa URL la care ascultă. Dacă deschideți http://127.0.0.1:6006, ar trebui să vedeți opt parcele similare cu acestea:

Încheierea

train() face tot antrenamentul. Mai întâi creăm modelul și reluăm tamponul. Apoi, într-o buclă foarte asemănătoare cu cea de la see.py , interacționăm cu mediul și stocăm experiențe în buffer. Ceea ce este important este că urmăm o politică lacomă de epsilon. Am putea alege întotdeauna cea mai bună acțiune în funcție de funcția $Q$; cu toate acestea, acest lucru descurajează explorarea, ceea ce dăunează performanței generale. Deci, pentru a impune explorarea cu probabilitate epsilon, efectuăm acțiuni aleatorii:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon a fost setat la 1%. După 2000 de experiențe, reluarea se umple suficient pentru a începe antrenamentul. O facem apelând fit_batch() cu un lot aleatoriu de experiențe eșantionate din buffer-ul de reluare:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

La fiecare 20.000 de pași, evaluăm și înregistrăm rezultatele (evaluarea este cu epsilon = 0 , politică total lacomă):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

Întregul cod are aproximativ 300 de linii, iar run.py conține aproximativ 250 dintre cele mai importante.

Se poate observa că există o mulțime de hiperparametri:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Și chiar nu sunt toate. Există și o arhitectură de rețea - am folosit două straturi ascunse cu 32 de neuroni, activări ReLU și optimizator Adam, dar există o mulțime de alte opțiuni. Chiar și schimbările mici pot avea un impact uriaș asupra antrenamentului. Se poate petrece mult timp pentru reglarea hiperparametrilor. Într-o competiție OpenAI recentă, un concurent pe locul doi a aflat că este posibil să dubleze aproape scorul lui Rainbow după reglarea hiperparametrului. Desigur, trebuie să ne amintim că este ușor să supraîncărcați. În prezent, algoritmii de întărire se luptă cu transferul de cunoștințe în medii similare. Mașina noastră de munte nu se generalizează la toate tipurile de munți în acest moment. Puteți modifica mediul OpenAI Gym și puteți vedea cât de mult se poate generaliza agentul.

Un alt exercițiu va fi să găsești un set de hiperparametri mai bun decât al meu. Cu siguranță este posibil. Cu toate acestea, o singură cursă de antrenament nu va fi suficientă pentru a aprecia dacă schimbarea dvs. este o îmbunătățire. De obicei, există o diferență mare între cursele de antrenament; varianța este mare. Ai nevoie de multe alergări pentru a determina că ceva este mai bun. Dacă doriți să citiți mai multe despre un subiect atât de important precum reproductibilitatea, vă încurajez să citiți Deep Reinforcement Learning that Matters. În loc să reglam manual, putem automatiza acest proces într-o oarecare măsură – dacă suntem dispuși să cheltuim mai multă putere de calcul pentru problemă. O abordare simplă este să pregătiți un interval promițător de valori pentru unii hiperparametri și apoi să rulați o căutare în grilă (verificarea combinațiilor acestora), cu antrenamente rulând în paralel. Paralelizarea în sine este un subiect important în sine, deoarece este crucială pentru performanță ridicată.

Deep $Q$-learning reprezintă o mare familie de algoritmi de învățare prin consolidare care utilizează iterația valorii. Am încercat să aproximăm funcția $Q$ și am folosit-o într-un mod lacom de cele mai multe ori. Există o altă familie care folosește iterația politicii. Ei nu se concentrează pe aproximarea funcției $Q$, ci pe găsirea directă a politicii optime $π^*$. Pentru a vedea unde se potrivește iterația valorii în peisajul algoritmilor de învățare prin consolidare:

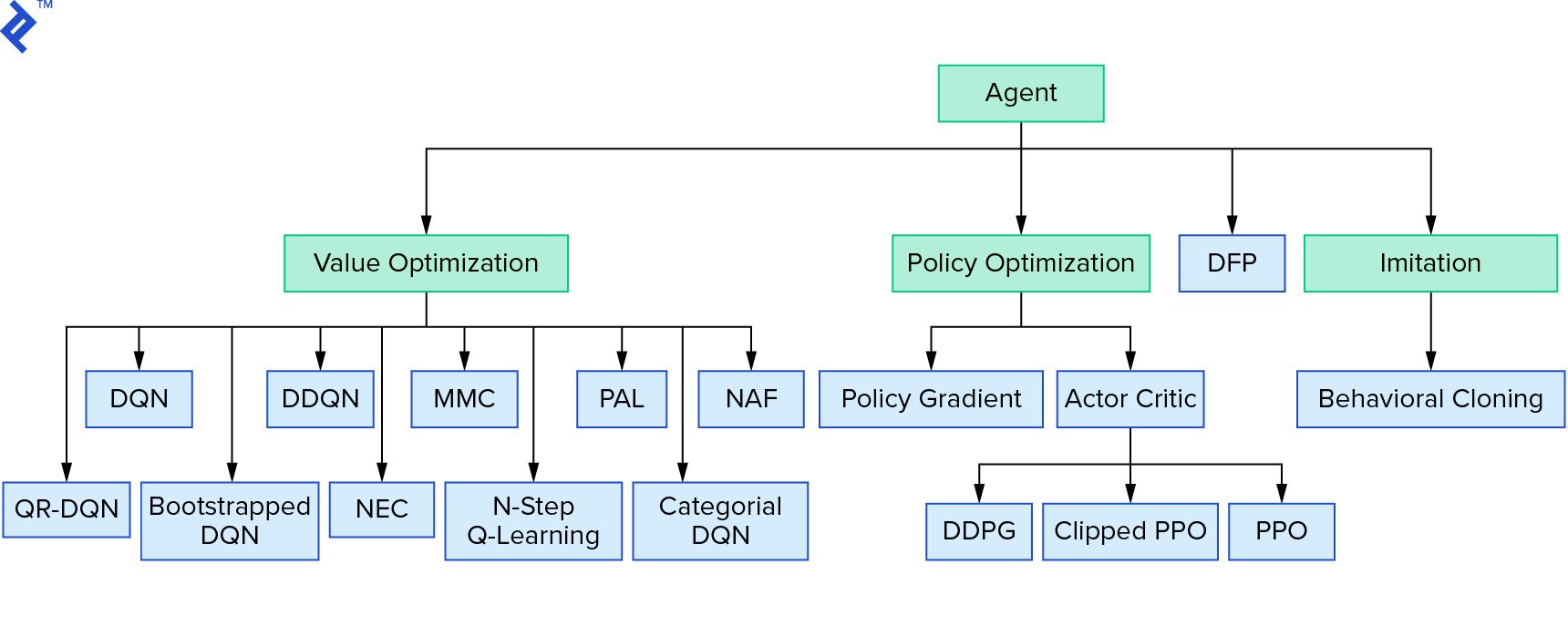
Gândurile tale ar putea fi că învățarea de întărire profundă pare fragilă. vei avea dreptate; sunt multe probleme. Puteți face referire la Învățarea prin întărire profundă nu funcționează încă și Învățarea prin întărire nu a funcționat niciodată, iar „deep” a ajutat doar puțin.

Aceasta încheie tutorialul. Am implementat propriul nostru DQN de bază în scopuri de învățare. Cod foarte asemănător poate fi folosit pentru a obține performanțe bune în unele dintre jocurile Atari. În aplicațiile practice, se iau adesea implementări testate, de înaltă performanță, de exemplu, una din liniile de bază OpenAI. Dacă doriți să vedeți ce provocări se poate confrunta atunci când încercați să aplicați învățarea prin consolidare profundă într-un mediu mai complex, puteți citi Abordarea noastră NIPS 2017: Învățare să alergați. Dacă doriți să aflați mai multe într-un mediu de competiție distractiv, aruncați o privire la Competițiile NIPS 2018 sau crowdai.org.

Dacă sunteți pe cale să deveniți un expert în învățarea automată și doriți să vă aprofundați cunoștințele în domeniul învățării supravegheate, consultați Analiza video de învățare automată: Identificarea peștilor pentru un experiment distractiv de identificare a peștilor.