Menyelam Jauh ke dalam Pembelajaran Penguatan

Mari selami lebih dalam tentang pembelajaran penguatan. Pada artikel ini, kita akan mengatasi masalah konkret dengan perpustakaan modern seperti TensorFlow, TensorBoard, Keras, dan gym OpenAI. Anda akan melihat bagaimana menerapkan salah satu algoritme dasar yang disebut deep $Q$-learning untuk mempelajari cara kerjanya. Mengenai perangkat keras, seluruh kode akan bekerja pada PC biasa dan menggunakan semua inti CPU yang ditemukan (ini ditangani langsung oleh TensorFlow).

Masalahnya disebut Mobil Gunung: Sebuah mobil berada di trek satu dimensi, diposisikan di antara dua gunung. Tujuannya adalah untuk mendaki gunung di sebelah kanan (mencapai bendera). Namun, mesin mobil tidak cukup kuat untuk mendaki gunung dalam sekali jalan. Oleh karena itu, satu-satunya cara untuk berhasil adalah dengan bergerak maju mundur untuk membangun momentum.

Masalah ini dipilih karena cukup sederhana untuk menemukan solusi dengan pembelajaran penguatan dalam hitungan menit pada satu inti CPU. Namun, itu cukup kompleks untuk menjadi perwakilan yang baik.

Pertama, saya akan memberikan ringkasan singkat tentang apa yang dilakukan pembelajaran penguatan secara umum. Kemudian, kami akan membahas istilah-istilah dasar dan mengungkapkan masalah kami dengan mereka. Setelah itu, saya akan menjelaskan algoritma deep $Q$-learning dan kami akan mengimplementasikannya untuk memecahkan masalah.

Dasar-dasar Pembelajaran Penguatan

Pembelajaran penguatan dengan kata yang paling sederhana adalah belajar dengan coba-coba. Karakter utama disebut "agen", yang akan menjadi mobil dalam masalah kita. Agen membuat tindakan di lingkungan dan diberikan kembali pengamatan baru dan hadiah untuk tindakan itu. Tindakan yang mengarah ke imbalan yang lebih besar diperkuat, oleh karena itu namanya. Seperti banyak hal lain dalam ilmu komputer, yang satu ini juga terinspirasi dari mengamati makhluk hidup.

Interaksi agen dengan lingkungan diringkas dalam grafik berikut:

Agen mendapatkan observasi dan reward atas tindakan yang dilakukan. Kemudian ia membuat tindakan lain dan mengambil langkah kedua. Lingkungan sekarang mengembalikan (mungkin) pengamatan dan penghargaan yang sedikit berbeda. Ini berlanjut sampai keadaan terminal tercapai, ditandai dengan mengirimkan "selesai" ke agen. Seluruh urutan pengamatan > tindakan > pengamatan_berikutnya > imbalan disebut episode (atau lintasan).

Kembali ke Mobil Gunung kami: mobil kami adalah agen. Lingkungan adalah dunia kotak hitam pegunungan satu dimensi. Aksi mobil bermuara hanya pada satu angka: jika positif, mesin mendorong mobil ke kanan. Jika negatif, itu mendorong mobil ke kiri. Agen merasakan lingkungan melalui pengamatan: posisi dan kecepatan X mobil. Jika kita ingin mobil kita melaju di puncak gunung, kita mendefinisikan hadiah dengan cara yang nyaman: Agen mendapatkan -1 untuk hadiahnya untuk setiap langkah yang belum mencapai tujuan. Ketika mencapai tujuan, episode berakhir. Jadi sebenarnya agen itu dihukum karena tidak berada di posisi yang kita inginkan. Semakin cepat dia mencapainya, semakin baik baginya. Tujuan agen adalah untuk memaksimalkan total hadiah, yang merupakan jumlah hadiah dari satu episode. Jadi jika mencapai titik yang diinginkan setelah, misalnya 110 langkah, menerima pengembalian total -110, yang akan menjadi hasil yang bagus untuk Mobil Gunung, karena jika tidak mencapai tujuan, maka itu dihukum untuk 200 langkah (oleh karena itu, pengembalian -200).

Ini adalah seluruh rumusan masalah. Sekarang, kita dapat memberikannya pada algoritme, yang sudah cukup kuat untuk menyelesaikan masalah seperti itu dalam hitungan menit (jika disetel dengan baik). Perlu dicatat bahwa kami tidak memberi tahu agen cara mencapai tujuan. Kami bahkan tidak memberikan petunjuk (heuristik). Agen akan menemukan cara (kebijakan) untuk menang sendiri.

Menyiapkan Lingkungan

Pertama, salin seluruh kode tutorial ke disk Anda:

 git clone https://github.com/AdamStelmaszczyk/rl-tutorial cd rl-tutorial

Sekarang, kita perlu menginstal paket Python yang akan kita gunakan. Untuk tidak menginstalnya di ruang pengguna Anda (dan berisiko tabrakan), kami akan membuatnya bersih dan menginstalnya di lingkungan conda. Jika Anda belum menginstal conda, ikuti https://conda.io/docs/user-guide/install/index.html.

Untuk membuat lingkungan conda kami:

 conda create -n tutorial python=3.6.5 -y

Untuk mengaktifkannya:

 source activate tutorial

Anda akan melihat (tutorial) di dekat prompt Anda di shell. Artinya lingkungan conda dengan nama “tutorial” sudah aktif. Mulai sekarang, semua perintah harus dijalankan dalam lingkungan conda itu.

Sekarang, kita dapat menginstal semua dependensi di lingkungan konda kedap udara kita:

 pip install -r requirements.txt

Kami selesai dengan instalasi, jadi mari kita jalankan beberapa kode. Kita tidak perlu menerapkan lingkungan Mountain Car sendiri; perpustakaan OpenAI Gym menyediakan implementasi itu. Mari kita lihat agen acak (agen yang mengambil tindakan acak) di lingkungan kita:

 import gym env = gym.make('MountainCar-v0') done = True episode = 0 episode_return = 0.0 for episode in range(5): for step in range(200): if done: if episode > 0: print("Episode return: ", episode_return) obs = env.reset() episode += 1 episode_return = 0.0 env.render() else: obs = next_obs action = env.action_space.sample() next_obs, reward, done, _ = env.step(action) episode_return += reward env.render()

Ini adalah file see.py ; untuk menjalankannya, jalankan:

 python see.py

Anda akan melihat mobil akan bolak-balik secara acak. Setiap episode akan terdiri dari 200 langkah; pengembalian total akan menjadi -200.

Sekarang kita perlu mengganti tindakan acak dengan sesuatu yang lebih baik. Ada banyak algoritma yang bisa digunakan. Untuk tutorial pengantar, saya pikir pendekatan yang disebut deep $Q$-learning cocok. Memahami metode itu memberikan dasar yang kuat untuk mempelajari pendekatan lain.

$Q$-belajar mendalam

Algoritma yang akan kita gunakan pertama kali dijelaskan pada tahun 2013 oleh Mnih et al. dalam Bermain Atari dengan Pembelajaran Penguatan Mendalam dan dipoles dua tahun kemudian dalam kontrol tingkat Manusia melalui pembelajaran penguatan mendalam. Banyak karya lain dibangun di atas hasil tersebut, termasuk algoritma terkini Rainbow (2017):

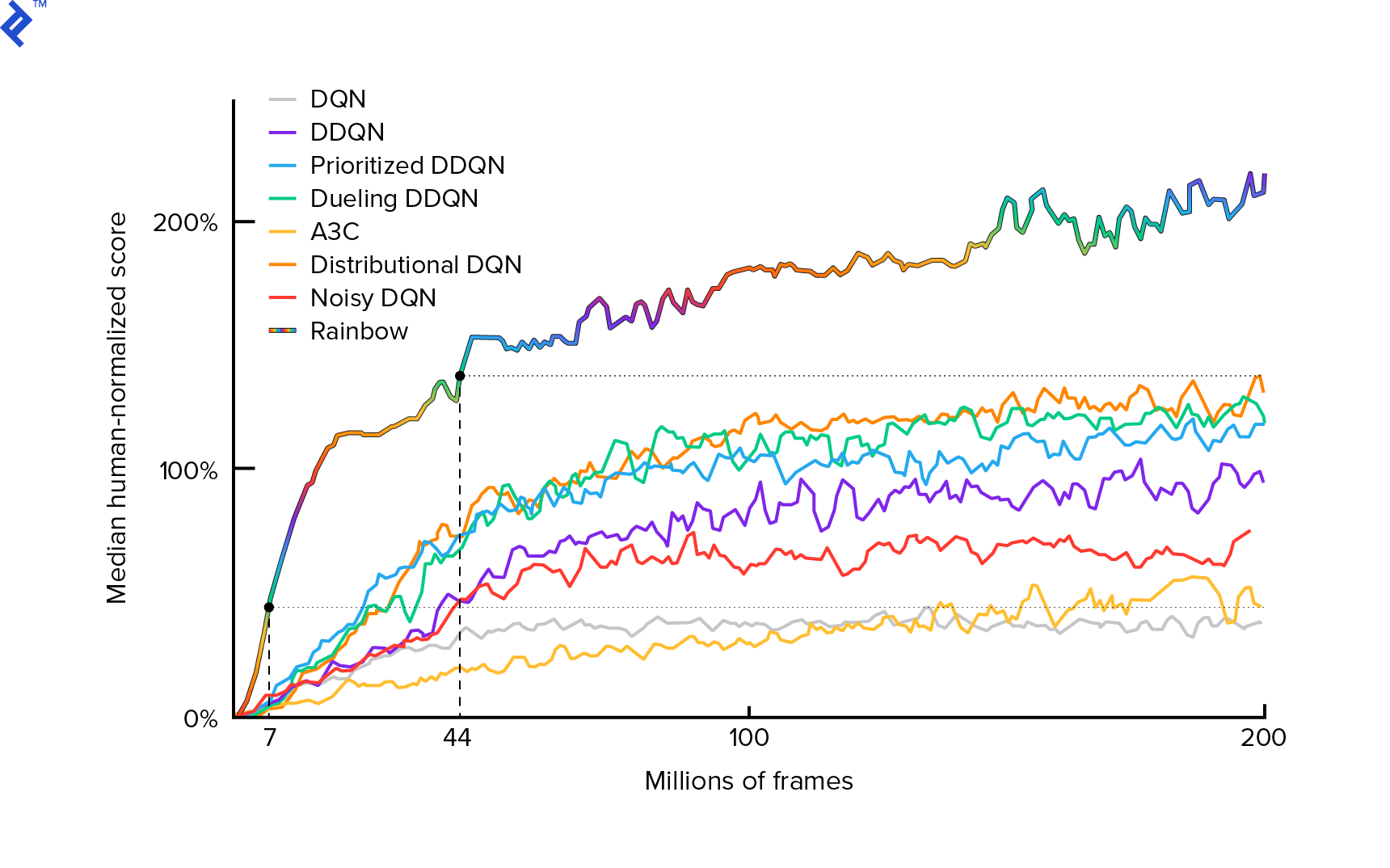
Rainbow mencapai kinerja manusia super di banyak game Atari 2600. Kami akan fokus pada versi DQN dasar, dengan sejumlah perbaikan tambahan sekecil mungkin, untuk menjaga tutorial ini dalam ukuran yang wajar.

Kebijakan, biasanya dilambangkan $π(s)$, adalah fungsi yang mengembalikan probabilitas untuk mengambil tindakan individu dalam keadaan tertentu $s$. Jadi, misalnya, kebijakan Mountain Car acak kembali untuk negara bagian apa pun: 50% kiri, 50% kanan. Selama bermain game, kami mengambil sampel dari kebijakan tersebut (distribusi) untuk mendapatkan tindakan nyata.

$Q$-learning (Q adalah untuk Kualitas) mengacu pada fungsi nilai tindakan yang dilambangkan $Q_π(s, a)$. Ini mengembalikan total pengembalian dari keadaan tertentu $s$, memilih tindakan $a$, mengikuti kebijakan konkret $π$. Pengembalian total adalah jumlah dari semua hadiah dalam satu episode (lintasan).

Jika kita mengetahui fungsi $Q$ yang optimal, dilambangkan dengan $Q^*$, kita dapat menyelesaikan permainan dengan mudah. Kami hanya akan mengikuti tindakan dengan nilai tertinggi $Q^*$, yaitu, pengembalian yang diharapkan tertinggi. Ini menjamin bahwa kami akan mencapai pengembalian setinggi mungkin.

Namun, kita sering tidak tahu $Q^*$. Dalam kasus seperti itu, kita dapat memperkirakan—atau “mempelajarinya”—dari interaksi dengan lingkungan. Ini adalah bagian "$Q$-learning" dalam namanya. Ada juga kata "dalam" di dalamnya karena, untuk mendekati fungsi itu, kita akan menggunakan jaringan saraf dalam, yang merupakan pendekatan fungsi universal. Jaringan saraf dalam yang mendekati nilai $Q$ diberi nama Deep Q-Networks (DQN). Dalam lingkungan sederhana (dengan jumlah status yang sesuai dengan memori), seseorang dapat menggunakan tabel alih-alih jaring saraf untuk mewakili fungsi $Q$, dalam hal ini akan diberi nama "tabular $Q$-learning."

Jadi tujuan kita sekarang adalah memperkirakan fungsi $Q^*$. Kami akan menggunakan persamaan Bellman:

\[Q(s, a) = r + \space \textrm{max}_{a'} Q(s', a')\]

$s'$ adalah keadaan setelah $s$. $γ$ (gamma), biasanya 0,99, adalah faktor diskon (ini adalah hyperparameter). Ini menempatkan bobot yang lebih kecil pada imbalan di masa depan (karena mereka kurang pasti daripada imbalan langsung dengan $Q$ kita yang tidak sempurna). Persamaan Bellman adalah inti dari pembelajaran $Q$ yang mendalam. Dikatakan bahwa nilai $Q$ untuk keadaan dan tindakan tertentu adalah hadiah yang diterima $r$ setelah melakukan tindakan $a$ ditambah nilai $Q$ tertinggi untuk keadaan yang kita dapatkan di $s'$. Yang tertinggi adalah dalam arti bahwa kita memilih tindakan $a'$, yang mengarah ke total pengembalian tertinggi dari $s'$.

Dengan persamaan Bellman, kita dapat menggunakan pembelajaran terawasi untuk memperkirakan $Q^*$. Fungsi $Q$ akan direpresentasikan (diparametrikan) oleh bobot jaringan saraf yang dilambangkan sebagai $θ$ (theta). Implementasi langsung akan mengambil status dan tindakan sebagai input jaringan dan output nilai-Q. Inefisiensinya adalah jika kita ingin mengetahui nilai $Q$ untuk semua tindakan dalam keadaan tertentu, kita perlu memanggil $Q$ sebanyak tindakan yang ada. Ada cara yang jauh lebih baik: untuk mengambil hanya status sebagai input dan output $Q$-nilai untuk semua tindakan yang mungkin. Berkat itu, kita bisa mendapatkan nilai $Q$ untuk semua tindakan hanya dalam satu umpan maju.

Kami mulai melatih jaringan $Q$ dengan bobot acak. Dari lingkungan, kami memperoleh banyak transisi (atau "pengalaman"). Ini adalah tupel (status, tindakan, status berikutnya, hadiah) atau, singkatnya, ($s$, $a$, $s'$, $r$). Kami menyimpan ribuan dari mereka dalam buffer cincin yang disebut "pengalaman replay." Kemudian, kami mengambil sampel pengalaman dari buffer itu dengan keinginan agar persamaan Bellman berlaku untuk mereka. Kita bisa saja melewatkan buffer dan menerapkan pengalaman satu per satu (ini disebut “online” atau “on-policy”); masalahnya adalah bahwa pengalaman berikutnya sangat berkorelasi satu sama lain dan DQN berlatih dengan buruk ketika ini terjadi. Itulah mengapa replay pengalaman diperkenalkan (pendekatan "offline", "di luar kebijakan") untuk memecahkan korelasi data ini. Kode implementasi ring buffer kami yang paling sederhana dapat ditemukan di file replay_buffer.py , saya mendorong Anda untuk membacanya.

Pada awalnya, karena bobot jaringan saraf kita acak, nilai ruas kiri persamaan Bellman akan jauh dari ruas kanan. Perbedaan kuadrat akan menjadi fungsi kerugian kita. Kami akan meminimalkan fungsi kerugian dengan mengubah bobot jaringan saraf $θ$. Mari kita tuliskan fungsi kerugian kita:

\[L(θ) = [Q(s, a) - r - \space \textrm{max}_{a'}Q(s', a')]^2\]

Ini adalah persamaan Bellman yang ditulis ulang. Katakanlah kita mencicipi pengalaman ($s$, kiri, $s'$, -1) dari tayangan ulang pengalaman Mountain Car. Kami melakukan forward pass melalui jaringan $Q$ kami dengan status $s$ dan untuk tindakan yang tersisa memberi kami -120, misalnya. Jadi, $Q(s, \textrm{left}) = -120$. Kemudian kita memasukkan $s'$ ke jaringan, yang memberi kita, misalnya, -130 untuk kiri dan -122 untuk kanan. Jadi jelas tindakan terbaik untuk $s'$ adalah benar, jadi $\textrm{max}_{a'}Q(s', a') = -122$. Kita tahu $r$, ini adalah hadiah yang sebenarnya, yaitu -1. Jadi prediksi jaringan $Q$ kami sedikit salah, karena $L(θ) = [-120 - 1 + 0,99 122]^2 = (-0,22^2) = 0,0484$. Jadi kami menyebarkan kesalahan ke belakang dan memperbaiki bobot $θ$ sedikit. Jika kita menghitung kerugian lagi untuk pengalaman yang sama, sekarang akan lebih rendah.

Satu pengamatan penting sebelum kita pergi ke kode. Mari kita perhatikan bahwa, untuk memperbarui DQN kita, kita akan melakukan dua forward pass pada DQN… itu sendiri. Hal ini sering menyebabkan pembelajaran tidak stabil. Untuk mengatasi itu, untuk prediksi $Q$ state selanjutnya, kami tidak menggunakan DQN yang sama. Kami menggunakan versi yang lebih lama, yang dalam kode disebut target_model (bukan model , menjadi DQN utama). Berkat itu, kami memiliki target yang stabil. Kami memperbarui target_model dengan menyetelnya ke bobot model setiap 1000 langkah. Tetapi model memperbarui setiap langkah.

Mari kita lihat kode yang membuat model DQN:

 def create_model(env): n_actions = env.action_space.n obs_shape = env.observation_space.shape observations_input = keras.layers.Input(obs_shape, name='observations_input') action_mask = keras.layers.Input((n_actions,), name='action_mask') hidden = keras.layers.Dense(32, activation='relu')(observations_input) hidden_2 = keras.layers.Dense(32, activation='relu')(hidden) output = keras.layers.Dense(n_actions)(hidden_2) filtered_output = keras.layers.multiply([output, action_mask]) model = keras.models.Model([observations_input, action_mask], filtered_output) optimizer = keras.optimizers.Adam(lr=LEARNING_RATE, clipnorm=1.0) model.compile(optimizer, loss='mean_squared_error') return model

Pertama, fungsi mengambil dimensi tindakan dan ruang observasi dari lingkungan OpenAI Gym yang diberikan. Penting untuk mengetahui, misalnya, berapa banyak keluaran yang akan dimiliki jaringan kita. Itu harus sama dengan jumlah tindakan. Tindakan adalah satu kode panas:

 def one_hot_encode(n, action): one_hot = np.zeros(n) one_hot[int(action)] = 1 return one_hot

Jadi (misalnya) kiri akan menjadi [1, 0] dan kanan akan menjadi [0, 1].

Kita bisa melihat observasi yang dilewatkan sebagai input. Kami juga meneruskan action_mask sebagai input kedua. Mengapa? Saat menghitung $Q(s,a)$, kita perlu mengetahui nilai $Q$ hanya untuk satu tindakan yang diberikan, tidak semuanya. action_mask berisi 1 untuk tindakan yang ingin kita sampaikan ke output DQN. Jika action_mask memiliki 0 untuk beberapa tindakan, maka nilai $Q$ yang sesuai akan di-nolkan pada output. Lapisan filtered_output melakukan itu. Jika kita ingin semua nilai $Q$ (untuk perhitungan maksimal), kita bisa melewatkan semuanya.

Kode menggunakan keras.layers.Dense untuk mendefinisikan layer yang terhubung penuh. Keras adalah library Python untuk abstraksi tingkat yang lebih tinggi di atas TensorFlow. Di bawah tenda, Keras membuat grafik TensorFlow, dengan bias, inisialisasi bobot yang tepat, dan hal-hal tingkat rendah lainnya. Kita bisa saja menggunakan TensorFlow mentah untuk mendefinisikan grafik, tetapi itu tidak akan menjadi satu baris.

Jadi pengamatan diteruskan ke lapisan tersembunyi pertama, dengan aktivasi ReLU (unit linier yang diperbaiki). ReLU(x) hanyalah fungsi $\textrm{max}(0, x)$. Lapisan itu sepenuhnya terhubung dengan lapisan identik kedua, hidden_2 . Lapisan keluaran menurunkan jumlah neuron ke jumlah tindakan. Pada akhirnya, kami memiliki filtered_output , yang hanya mengalikan output dengan action_mask .

Untuk menemukan bobot $θ$, kita akan menggunakan pengoptimal bernama “Adam” dengan kerugian kesalahan kuadrat rata-rata.

Memiliki model, kita dapat menggunakannya untuk memprediksi nilai $Q$ untuk observasi status yang diberikan:

 def predict(env, model, observations): action_mask = np.ones((len(observations), env.action_space.n)) return model.predict(x=[observations, action_mask])

Kami ingin $Q$-nilai untuk semua tindakan, jadi action_mask adalah vektornya.

Untuk melakukan pelatihan yang sebenarnya, kita akan menggunakan fit_batch() :

 def fit_batch(env, model, target_model, batch): observations, actions, rewards, next_observations, dones = batch # Predict the Q values of the next states. Passing ones as the action mask. next_q_values = predict(env, target_model, next_observations) # The Q values of terminal states is 0 by definition. next_q_values[dones] = 0.0 # The Q values of each start state is the reward + gamma * the max next state Q value q_values = rewards + DISCOUNT_FACTOR_GAMMA * np.max(next_q_values, axis=1) one_hot_actions = np.array([one_hot_encode(env.action_space.n, action) for action in actions]) history = model.fit( x=[observations, one_hot_actions], y=one_hot_actions * q_values[:, None], batch_size=BATCH_SIZE, verbose=0, ) return history.history['loss'][0]

Batch berisi BATCH_SIZE pengalaman. next_q_values ​​adalah $Q(s, a)$. q_values ​​adalah $r + \space \textrm{max}_{a'}Q(s', a')$ dari persamaan Bellman. Tindakan yang kami ambil adalah satu kode panas dan diteruskan sebagai action_mask ke input saat memanggil model.fit() . $y$ adalah huruf umum untuk "target" dalam pembelajaran terawasi. Di sini kita melewati q_values ​​. Saya melakukan q_values[:. None] q_values[:. None] untuk menambah dimensi larik karena harus sesuai dengan dimensi larik one_hot_actions . Ini disebut notasi irisan jika Anda ingin membaca lebih lanjut tentangnya.

Kami mengembalikan kerugian untuk menyimpannya di file log TensorBoard dan kemudian memvisualisasikannya. Ada banyak hal lain yang akan kita pantau: berapa langkah per detik yang kita buat, total penggunaan RAM, berapa rata-rata pengembalian episode, dll. Mari kita lihat plot-plot itu.

Berlari

Untuk memvisualisasikan file log TensorBoard, pertama-tama kita harus memilikinya. Jadi mari kita jalankan pelatihannya:

 python run.py

Ini pertama-tama akan mencetak ringkasan model kami. Kemudian akan membuat direktori log dengan tanggal saat ini dan memulai pelatihan. Setiap 2000 langkah, logline akan dicetak seperti ini:

 episode 10 steps 200/2001 loss 0.3346639 return -200.0 in 1.02s 195.7 steps/s 9.0/15.6 GB RAM

Setiap 20.000, kami akan mengevaluasi model kami pada 10.000 langkah:

 Evaluation 100%|█████████████████████████████████████████████████████████████████████████████████| 10000/10000 [00:07<00:00, 1254.40it/s] episode 677 step 120000 episode_return_avg -136.750 avg_max_q_value -56.004

Setelah 677 episode dan 120.000 langkah, rata-rata pengembalian episode meningkat dari -200 menjadi -136,75! Itu pasti belajar. Apa avg_max_q_value yang saya tinggalkan sebagai latihan yang baik untuk pembaca. Tapi ini adalah statistik yang sangat berguna untuk dilihat selama pelatihan.

Setelah 200.000 langkah, pelatihan kami selesai. Pada CPU empat inti saya, dibutuhkan sekitar 20 menit. Kita dapat melihat ke dalam direktori date-log , misalnya 06-07-18-39-log . Akan ada empat file model dengan ekstensi .h5 . Ini adalah cuplikan bobot grafik TensorFlow, kami menyimpannya setiap 50.000 langkah untuk kemudian melihat kebijakan yang kami pelajari. Untuk melihatnya:

 python run.py --model 06-08-18-42-log/06-08-18-42-200000.h5 --view

Untuk melihat kemungkinan flag lainnya: python run.py --help .

Sekarang, mobil melakukan pekerjaan yang jauh lebih baik untuk mencapai tujuan yang diinginkan. Di direktori date-log , ada juga file events.out.* . Ini adalah file tempat TensorBoard menyimpan datanya. Kami menulisnya menggunakan TensorBoardLogger paling sederhana yang didefinisikan di loggers.py. Untuk melihat file acara, kita perlu menjalankan server TensorBoard lokal:

 tensorboard --logdir=.

--logdir hanya menunjuk ke direktori di mana ada direktori log-tanggal, dalam kasus kami, ini akan menjadi direktori saat ini, jadi . . TensorBoard mencetak URL yang didengarkannya. Jika Anda membuka http://127.0.0.1:6006, Anda akan melihat delapan plot yang mirip dengan ini:

Membungkus

train() melakukan semua pelatihan. Kami pertama-tama membuat model dan memutar ulang buffer. Kemudian, dalam loop yang sangat mirip dengan loop dari see.py , kita berinteraksi dengan lingkungan dan menyimpan pengalaman di buffer. Yang penting adalah kita mengikuti kebijakan serakah epsilon. Kita selalu dapat memilih tindakan terbaik menurut fungsi $Q$; namun, hal itu menghambat eksplorasi, yang merusak kinerja secara keseluruhan. Jadi untuk menegakkan eksplorasi dengan probabilitas epsilon, kami melakukan tindakan acak:

 def greedy_action(env, model, observation): next_q_values = predict(env, model, observations=[observation]) return np.argmax(next_q_values) def epsilon_greedy_action(env, model, observation, epsilon): if random.random() < epsilon: action = env.action_space.sample() else: action = greedy_action(env, model, observation) return action

Epsilon diatur ke 1%. Setelah 2000 pengalaman, replay mengisi cukup untuk memulai pelatihan. Kami melakukannya dengan memanggil fit_batch() dengan kumpulan pengalaman acak yang diambil dari buffer replay:

 batch = replay.sample(BATCH_SIZE) loss = fit_batch(env, model, target_model, batch)

Setiap 20.000 langkah, kami mengevaluasi dan mencatat hasilnya (evaluasi dengan epsilon = 0 , kebijakan yang benar-benar rakus):

 if step >= TRAIN_START and step % EVAL_EVERY == 0: episode_return_avg = evaluate(env, model) q_values = predict(env, model, q_validation_observations) max_q_values = np.max(q_values, axis=1) avg_max_q_value = np.mean(max_q_values) print( "episode {} " "step {} " "episode_return_avg {:.3f} " "avg_max_q_value {:.3f}".format( episode, step, episode_return_avg, avg_max_q_value, )) logger.log_scalar('episode_return_avg', episode_return_avg, step) logger.log_scalar('avg_max_q_value', avg_max_q_value, step)

Keseluruhan kode terdiri dari sekitar 300 baris, dan run.py berisi sekitar 250 baris yang paling penting.

Orang dapat melihat ada banyak hyperparameters:

 DISCOUNT_FACTOR_GAMMA = 0.99 LEARNING_RATE = 0.001 BATCH_SIZE = 64 TARGET_UPDATE_EVERY = 1000 TRAIN_START = 2000 REPLAY_BUFFER_SIZE = 50000 MAX_STEPS = 200000 LOG_EVERY = 2000 SNAPSHOT_EVERY = 50000 EVAL_EVERY = 20000 EVAL_STEPS = 10000 EVAL_EPSILON = 0 TRAIN_EPSILON = 0.01 Q_VALIDATION_SIZE = 10000

Dan itu bahkan tidak semuanya. Ada juga arsitektur jaringan—kami menggunakan dua lapisan tersembunyi dengan 32 neuron, aktivasi ReLU, dan pengoptimal Adam, tetapi ada banyak opsi lain. Bahkan perubahan kecil dapat berdampak besar pada pelatihan. Banyak waktu dapat dihabiskan untuk menyetel hyperparameter. Dalam kompetisi OpenAI baru-baru ini, seorang kontestan tempat kedua menemukan kemungkinan untuk hampir menggandakan skor Rainbow setelah penyetelan hyperparameter. Secara alami, kita harus ingat bahwa overfit itu mudah. Saat ini, algoritma penguatan sedang berjuang dengan transfer pengetahuan ke lingkungan yang serupa. Mobil Gunung kami tidak menggeneralisasi ke semua jenis gunung saat ini. Anda sebenarnya dapat memodifikasi lingkungan OpenAI Gym dan melihat seberapa jauh agen dapat menggeneralisasi.

Latihan lain adalah menemukan set hyperparameter yang lebih baik daripada milik saya. Itu pasti mungkin. Namun, satu kali pelatihan tidak akan cukup untuk menilai apakah perubahan Anda merupakan peningkatan. Biasanya ada perbedaan besar antara latihan lari; variansnya besar. Anda akan membutuhkan banyak putaran untuk menentukan bahwa ada sesuatu yang lebih baik. Jika Anda ingin membaca lebih lanjut tentang topik penting seperti reproduktifitas, saya mendorong Anda untuk membaca Deep Reinforcement Learning that Matters. Alih-alih menyetel dengan tangan, kami dapat mengotomatiskan proses ini sampai batas tertentu—jika kami bersedia menghabiskan lebih banyak daya komputasi untuk masalah tersebut. Pendekatan sederhana adalah menyiapkan rentang nilai yang menjanjikan untuk beberapa hyperparameter dan kemudian menjalankan pencarian grid (memeriksa kombinasinya), dengan pelatihan yang berjalan secara paralel. Paralelisasi itu sendiri adalah topik besar tersendiri karena sangat penting untuk kinerja tinggi.

Deep $Q$-learning mewakili keluarga besar algoritme pembelajaran penguatan yang menggunakan iterasi nilai. Kami mencoba memperkirakan fungsi $Q$, dan kami sering menggunakannya dengan cara yang serakah. Ada keluarga lain yang menggunakan iterasi kebijakan. Mereka tidak fokus pada pendekatan fungsi $Q$, tetapi pada menemukan kebijakan optimal $π^*$ secara langsung. Untuk melihat di mana iterasi nilai cocok dalam lanskap algoritma pembelajaran penguatan:

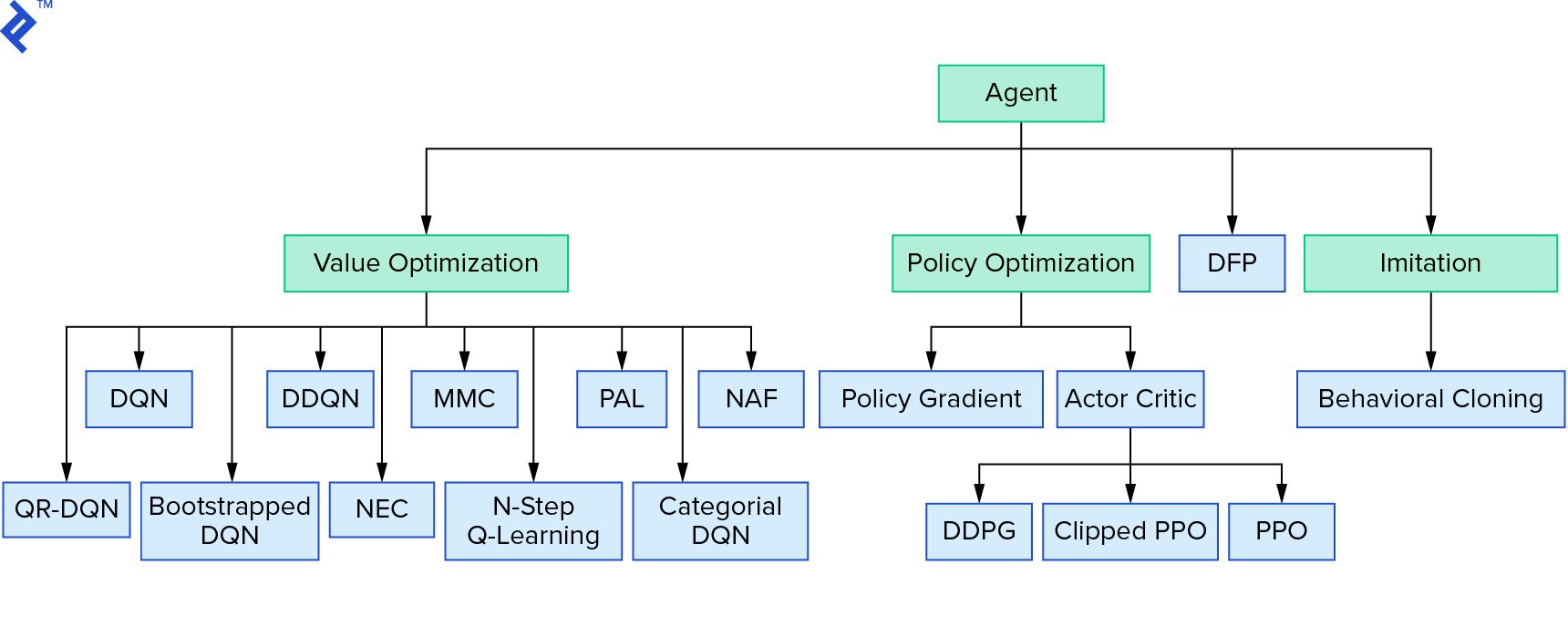
Pikiran Anda mungkin bahwa pembelajaran penguatan yang dalam terlihat rapuh. Anda akan benar; ada banyak masalah. Anda dapat merujuk ke Pembelajaran Penguatan Dalam Belum Berfungsi dan Pembelajaran Penguatan tidak pernah berhasil, dan 'dalam' hanya membantu sedikit.

Ini mengakhiri tutorial. Kami menerapkan DQN dasar kami sendiri untuk tujuan pembelajaran. Kode yang sangat mirip dapat digunakan untuk mencapai kinerja yang baik di beberapa game Atari. Dalam aplikasi praktis, seseorang sering mengambil implementasi kinerja tinggi yang teruji, misalnya, satu dari baseline OpenAI. Jika Anda ingin melihat tantangan apa yang dapat dihadapi seseorang ketika mencoba menerapkan pembelajaran penguatan dalam di lingkungan yang lebih kompleks, Anda dapat membaca pendekatan Our NIPS 2017: Learning to Run. Jika Anda ingin belajar lebih banyak dalam suasana kompetisi yang menyenangkan, lihat Kompetisi NIPS 2018 atau crowdai.org.

Jika Anda sedang dalam perjalanan untuk menjadi ahli pembelajaran mesin dan ingin memperdalam pengetahuan Anda dalam pembelajaran yang diawasi, lihat Analisis Video Pembelajaran Mesin: Mengidentifikasi Ikan untuk eksperimen menyenangkan dalam mengidentifikasi ikan.