Machines à vecteurs de support : types de SVM [explication de l'algorithme]

introduction

Tout comme d'autres algorithmes d'apprentissage automatique qui effectuent la tâche de classification (arbres de décision, forêt aléatoire, K-NN) et de régression, Support Vector Machine ou SVM un tel algorithme dans l'ensemble du pool. Il s'agit d'un algorithme d'apprentissage automatique supervisé (nécessite des ensembles de données étiquetés) qui est utilisé pour les problèmes liés à la classification ou à la régression.

Cependant, il est fréquemment appliqué dans les problèmes de classification. L'algorithme SVM implique le traçage de chaque élément de données sous forme de point. Le traçage est effectué dans un espace à n dimensions où n est le nombre de caractéristiques d'une donnée particulière. Ensuite, la classification est effectuée en trouvant l'hyperplan le plus approprié qui sépare efficacement les deux (ou plusieurs) classes.

Le terme vecteurs de support ne sont que les coordonnées d'une caractéristique individuelle. Pourquoi généraliser les points de données en tant que vecteurs, vous pouvez vous demander. Dans les problèmes du monde réel, il existe des ensembles de données de dimensions supérieures. Dans les dimensions supérieures (n-dimension), il est plus logique d'effectuer des manipulations arithmétiques vectorielles et matricielles plutôt que de les considérer comme des points.

Types de SVM

SVM linéaire : SVM linéaire est utilisé pour les données séparables linéairement, c'est-à-dire pour un ensemble de données qui peut être classé en deux catégories en utilisant une seule ligne droite. De tels points de données sont appelés données séparables linéairement, et le classificateur est utilisé décrit comme un classificateur SVM linéaire.

SVM non linéaire : le SVM non linéaire est utilisé pour les données non linéairement séparables, c'est-à-dire qu'une ligne droite ne peut pas être utilisée pour classer l'ensemble de données. Pour cela, nous utilisons quelque chose connu sous le nom d'astuce du noyau qui définit les points de données dans une dimension supérieure où ils peuvent être séparés à l'aide de plans ou d'autres fonctions mathématiques. Ces points de données sont appelés données non linéaires et le classificateur utilisé est appelé classificateur SVM non linéaire.

Algorithme pour SVM linéaire

Parlons d'un problème de classification binaire. La tâche consiste à classer efficacement un point de test dans l'une ou l'autre des classes aussi précisément que possible. Voici les étapes impliquées dans le processus SVM.

Tout d'abord, un ensemble de points appartenant aux deux classes est tracé et visualisé comme indiqué ci-dessous. Dans un espace 2D en appliquant simplement une ligne droite, nous pouvons diviser efficacement ces deux classes. Mais il peut y avoir plusieurs lignes qui permettent de classer ces classes. Il existe un ensemble de lignes ou d'hyperplans (lignes vertes) parmi lesquels choisir. La question évidente sera, parmi toutes ces lignées, quelle lignée convient à la classification ?

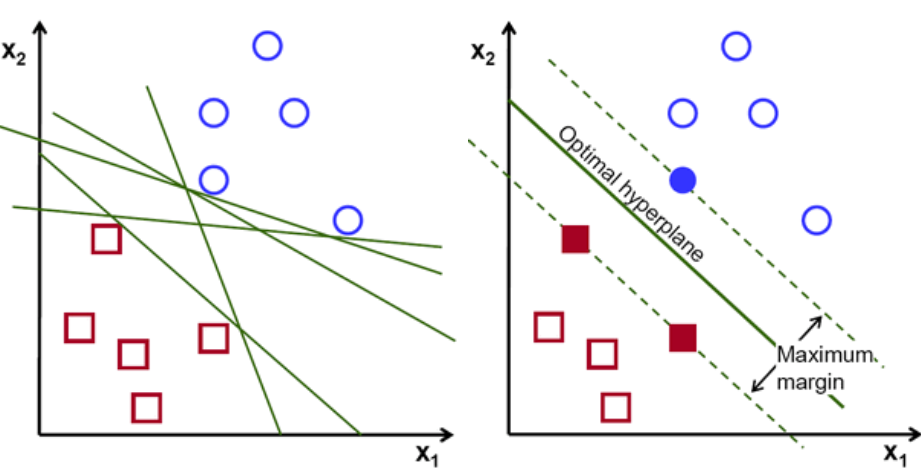
ensemble d'hyper-plans, Crédit image

En gros, sélectionnez l'hyper-plan qui sépare le mieux les deux classes. Pour ce faire, nous maximisons la distance entre le point de données le plus proche et l'hyper-plan. Plus la distance est grande, meilleur est l'hyperplan et de meilleurs résultats de classification s'ensuivent. On peut voir sur la figure ci-dessous que l'hyperplan sélectionné a la distance maximale du point le plus proche de chacune de ces classes.

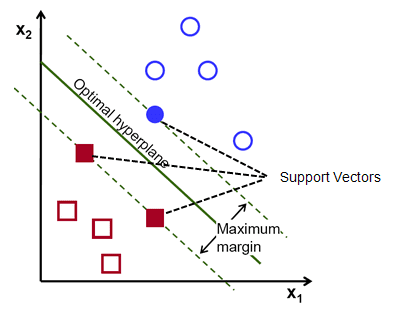
Pour rappel, les deux lignes pointillées qui vont parallèlement à l'hyperplan passant par les points les plus proches de chacune des classes sont appelées vecteurs supports de l'hyperplan. Or, la distance de séparation entre les vecteurs supports et l'hyperplan s'appelle une marge. Et le but de l'algorithme SVM est de maximiser cette marge. L'hyperplan optimal est l'hyperplan avec une marge maximale.

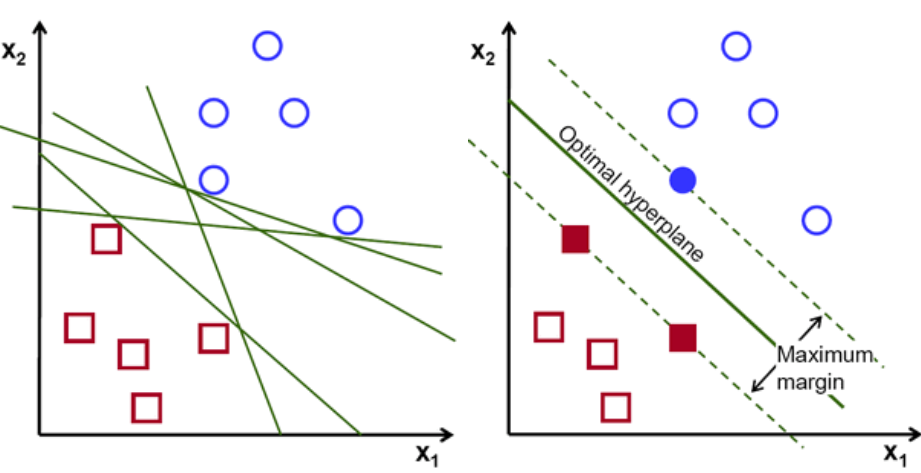
Crédit image

Prenons par exemple la classification des cellules comme bonnes et mauvaises. la cellule xᵢ est définie comme un Chacun de ces vecteurs de caractéristiques est étiqueté avec une classe yᵢ. La classe yᵢ peut être soit un +ve, soit un -ve (par exemple bon=1, pas bon =-1). L'équation de l'hyperplan est y= wx + b = 0. Où W et b sont des paramètres de ligne. L'équation précédente renvoie une valeur ≥ 1 pour les exemples de classe +ve et ≤-1 pour les exemples de classe -ve.

Mais, comment trouve-t-il cet hyperplan ? L'hyperplan est défini en trouvant les valeurs optimales w ou poids et b ou intercepter qui. Et ces valeurs optimales sont trouvées en minimisant la fonction de coût. Une fois que l'algorithme collecte ces valeurs optimales, le modèle SVM ou la fonction de ligne f(x) classe efficacement les deux classes.

En un mot, l'hyperplan optimal a l'équation w.x+b = 0. Le vecteur de support gauche a l'équation w.x+b=-1 et le vecteur de support droit a w.x+b=1.

Ainsi la distance d entre deux privilèges parallèles Ay = Bx + c1 et Ay = Bx + c2 est donnée par d = |C1–C2|/√A^2 + B^2. Avec cette formule en place, nous avons la distance entre les deux vecteurs de support sous la forme 2/||w||.

La fonction de coût pour SVM ressemble à l'équation ci-dessous :

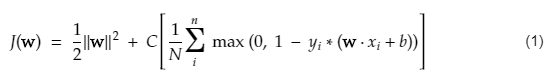
Crédit image

Fonction de perte SVM

Dans l'équation de la fonction de coût ci-dessus, le paramètre λ indique qu'un λ plus grand fournit une marge plus large, et qu'un λ plus petit donnerait une marge plus petite. De plus, le gradient de la fonction de coût est calculé et les poids sont mis à jour dans la direction qui abaisse la fonction perdue.

Lire : Algèbre linéaire pour l'apprentissage automatique : concepts critiques, pourquoi apprendre avant le ML

Algorithme pour SVM non linéaire

Dans le classificateur SVM, il est simple d'avoir un hyper-plan linéaire entre ces deux classes. Mais, une question intéressante qui se pose est de savoir si les données ne sont pas linéairement séparables, que faut-il faire ? Pour cela, l'algorithme SVM dispose d'une méthode appelée l'astuce du noyau.

La fonction du noyau SVM prend un espace d'entrée de faible dimension et le convertit en un espace de dimension supérieure. En termes simples, il convertit le problème non séparable en un problème séparable. Il effectue des transformations de données complexes en fonction des étiquettes ou des sorties qui les définissent

Regardez le diagramme ci-dessous pour mieux comprendre la transformation des données. L'ensemble de points de données sur la gauche n'est clairement pas linéairement séparable. Mais lorsque nous appliquons une fonction Φ à l'ensemble des points de données, nous obtenons des points de données transformés dans une dimension supérieure séparable via un plan.

Crédit image

Pour séparer des points de données non linéairement séparables, nous devons ajouter une dimension supplémentaire. Pour les données linéaires, deux dimensions ont été utilisées, c'est-à-dire x et y. Pour ces points de données, nous ajoutons une troisième dimension, disons z. Pour l'exemple ci-dessous soit z=x² +y².

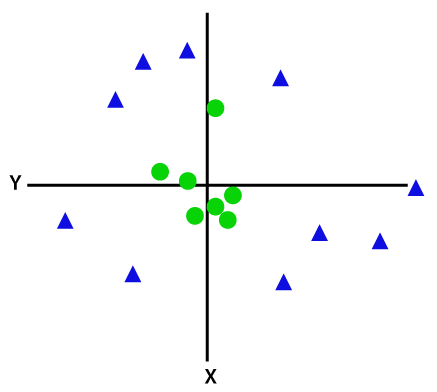
Crédit image

Cette fonction z ou la dimensionnalité ajoutée transforme l'espace échantillon et l'image ci-dessus deviendra comme suit :

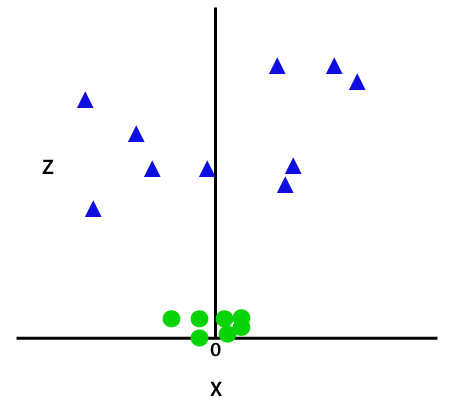
Crédit image

Après une analyse approfondie, il est évident que les points de données ci-dessus peuvent être séparés à l'aide d'une fonction de ligne droite parallèle à l'axe x ou inclinée à un angle. Différents types de fonctions de noyau sont présents - linéaire, non linéaire, polynomiale, fonction de base radiale (RBF) et sigmoïde.

Ce que RBF fait en termes simples est - si nous choisissons un point, le résultat d'un RBF sera la norme de la distance entre ce point et un point fixe. En d'autres termes, nous pouvons concevoir une dimension z avec les rendements de ce RBF, qui donne généralement la "hauteur" en fonction de la distance entre le point et un point.

Découvrez : 6 types de fonction d'activation dans les réseaux de neurones que vous devez connaître

Quel noyau choisir ?

Une bonne méthode pour déterminer quel noyau est le plus approprié consiste à créer divers modèles avec différents noyaux, puis à estimer chacune de leurs performances et, finalement, à comparer les résultats. Ensuite, vous choisissez le noyau avec les meilleurs résultats. Soyez particulier pour estimer les performances du modèle sur des observations différentes en utilisant la validation croisée K-Fold et considérez différentes mesures comme la précision, le score F1, etc.

SVM en Python et R

La méthode fit en python entraîne simplement le modèle SVM sur les données Xtrain et ytrain qui ont été séparées. Plus précisément, la méthode fit assemblera les données dans Xtrain et ytrain, et à partir de là, elle calculera les deux vecteurs de support.

Une fois ces vecteurs de support estimés, le modèle de classificateur est complètement configuré pour produire de nouvelles prédictions avec la fonction de prédiction car il n'a besoin que des vecteurs de support pour séparer les nouvelles données. Maintenant, vous pouvez obtenir des résultats différents en Python et en R, alors assurez-vous de vérifier la valeur du paramètre seed.

Conclusion

Dans cet article, nous avons examiné en détail l'algorithme Support Vector Machine. Merci pour votre temps. Connectez-vous pour plus d'articles de ce type.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.

À quels types de problèmes les modèles Support Vector Machine conviennent-ils ?

Les machines à vecteurs de support (SVM) fonctionnent mieux sur des données linéairement séparables, c'est-à-dire des données qui peuvent être séparées en deux classes distinctes à l'aide d'une ligne droite ou d'un hyperplan. L'une des utilisations les plus courantes de SVM est la reconnaissance faciale. La technique des eigenfaces est un exemple de SVM, qui réduit la dimensionnalité des images faciales et est utilisée pour la reconnaissance faciale. Cette technique est basée sur la prémisse que les visages peuvent être considérés comme des vecteurs dans un espace vectoriel de grande dimension et que la dimensionnalité est réduite en ajustant une hypersphère aux données. Cela nous permet de faire correspondre deux faces qui sont de taille différente ou qui ont pivoté. SVM est également utilisé dans la classification.

Quelles sont les applications des SVM dans la vie réelle ?

SVM peut-il être utilisé pour des données continues ?

SVM est utilisé pour créer un modèle de classification. Donc, si vous avez un classificateur, il doit fonctionner avec seulement deux classes. Si vous avez des données continues, vous devrez transformer ces données en classes, le processus s'appelle la réduction de la dimensionnalité. Par exemple, si vous avez quelque chose comme l'âge, la taille, le poids, le grade, etc., vous pouvez prendre la moyenne de ces données et la rapprocher d'une classe ou d'une autre, ce qui facilitera alors la classification.