Maszyny wektorów nośnych: rodzaje SVM [Objaśnienie algorytmu]

Wstęp

Podobnie jak inne algorytmy w uczeniu maszynowym realizujące zadania klasyfikacji (drzewa decyzyjne, las losowy, K-NN) i regresji, Support Vector Machine lub SVM jeden taki algorytm w całej puli. Jest to nadzorowany (wymaga oznaczonych zestawów danych) algorytm uczenia maszynowego, który jest używany do rozwiązywania problemów związanych z klasyfikacją lub regresją.

Jest jednak często stosowany w problemach klasyfikacyjnych. Algorytm SVM pociąga za sobą wykreślenie każdego elementu danych jako punktu. Wykres odbywa się w przestrzeni n-wymiarowej, gdzie n jest liczbą cech poszczególnych danych. Następnie przeprowadza się klasyfikację poprzez znalezienie najbardziej odpowiedniej hiperpłaszczyzny, która skutecznie oddziela dwie (lub więcej) klasy.

Termin wektory nośne to po prostu współrzędne pojedynczej cechy. Po co uogólniać punkty danych jako wektory, o które możesz zapytać. W rzeczywistych problemach istnieją zbiory danych o wyższych wymiarach. W wyższych wymiarach (wymiar n) bardziej sensowne jest wykonywanie operacji arytmetycznych na wektorach i macierzach niż traktowanie ich jako punktów.

Rodzaje SVM

Linear SVM : Linear SVM jest używany do danych, które można oddzielić liniowo, tj. dla zestawu danych, który można podzielić na dwie kategorie przy użyciu pojedynczej linii prostej. Takie punkty danych są określane jako dane liniowo separowalne, a klasyfikator jest używany jako klasyfikator liniowy SVM.

Nieliniowa SVM: Nieliniowa SVM jest używana dla danych, które są nieliniowo dającymi się oddzielić, tj. linia prosta nie może być użyta do klasyfikacji zbioru danych. W tym celu używamy czegoś znanego jako sztuczka jądra, która ustawia punkty danych w wyższym wymiarze, gdzie można je oddzielić za pomocą płaszczyzn lub innych funkcji matematycznych. Takie punkty danych są określane jako dane nieliniowe, a używany klasyfikator jest określany jako nieliniowy klasyfikator SVM.

Algorytm dla liniowej SVM

Porozmawiajmy o problemie klasyfikacji binarnej. Zadanie polega na tym, aby jak najdokładniej sklasyfikować punkt testowy w którejkolwiek z klas. Poniżej przedstawiono kroki związane z procesem SVM.

Po pierwsze, zestaw punktów należących do dwóch klas jest wykreślany i wizualizowany, jak pokazano poniżej. W przestrzeni dwuwymiarowej, po prostu stosując linię prostą, możemy efektywnie podzielić te dwie klasy. Ale może być wiele linii, które mogą klasyfikować te klasy. Do wyboru jest zestaw linii lub hiperpłaszczyzn (linie zielone). Oczywistym pytaniem będzie, która z tych wszystkich linii nadaje się do klasyfikacji?

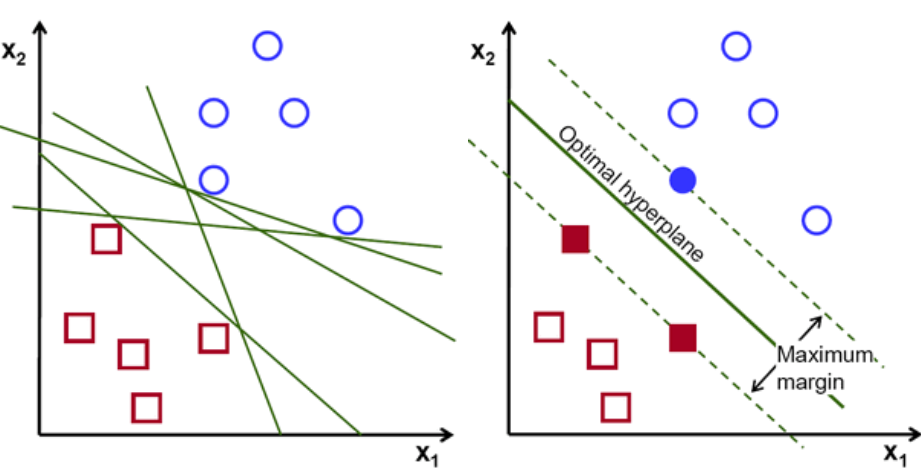
zestaw hiperpłaszczyzn, kredyt obrazu

Zasadniczo wybierz hiperpłaszczyznę, która lepiej oddziela dwie klasy. Robimy to, maksymalizując odległość między najbliższym punktem danych a hiperpłaszczyzną. Im większa odległość, tym lepsza jest hiperpłaszczyzna i uzyskuje się lepsze wyniki klasyfikacji. Na poniższym rysunku widać, że wybrana hiperpłaszczyzna ma maksymalną odległość od najbliższego punktu z każdej z tych klas.

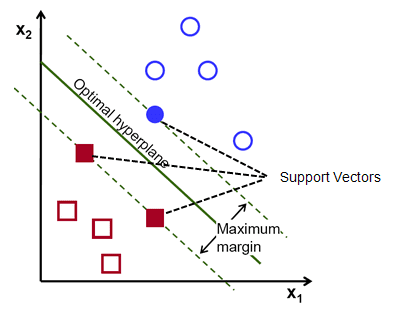
Przypominamy, że dwie kropkowane linie biegnące równolegle do hiperpłaszczyzny przecinające najbliższe punkty każdej z klas są określane jako wektory nośne hiperpłaszczyzny. Teraz odległość separacji między wektorami nośnymi a hiperpłaszczyzną nazywa się marginesem. A celem algorytmu SVM jest maksymalizacja tego marginesu. Optymalna hiperpłaszczyzna to hiperpłaszczyzna z maksymalnym marginesem.

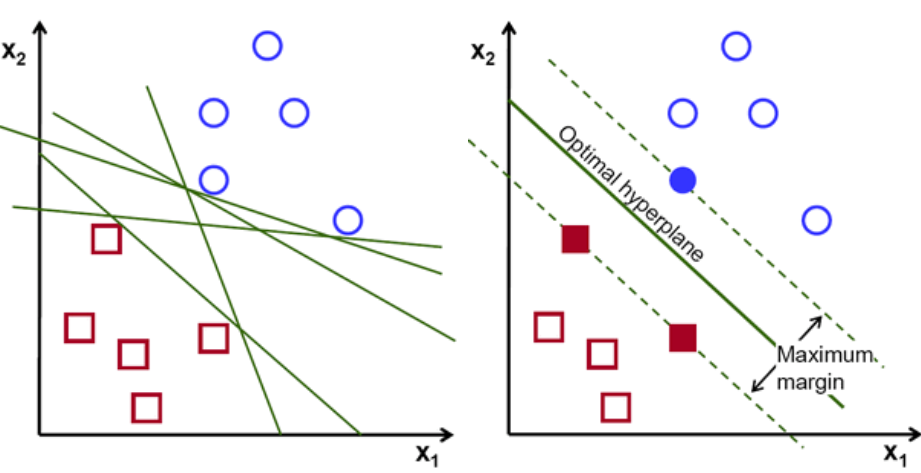
Kredyt obrazu

Weźmy na przykład klasyfikację komórek jako dobrych i złych. komórka xᵢ jest zdefiniowana jako Każdy z tych wektorów cech jest oznaczony klasą yᵢ. Klasa yᵢ może mieć wartość +ve lub -ve (np. dobra=1, niedobra =-1). Równanie hiperpłaszczyzny to y= wx + b = 0. Gdzie W i b są parametrami linii. Wcześniejsze równanie zwraca wartość ≥ 1 dla przykładów dla klasy +ve i ≤-1 dla przykładów klasy -ve.

Ale jak znajduje tę hiperpłaszczyznę? Hiperpłaszczyzna jest definiowana poprzez znalezienie optymalnych wartości w lub wag i b lub przecięcia które. A te optymalne wartości można znaleźć, minimalizując funkcję kosztu. Gdy algorytm zbierze te optymalne wartości, model SVM lub funkcja liniowa f(x) skutecznie klasyfikuje te dwie klasy.

W skrócie, optymalna hiperpłaszczyzna ma równanie w.x+b = 0. Lewy wektor podparcia ma równanie w.x+b=-1, a prawy wektor podparcia ma w.x+b=1.

Zatem odległość d pomiędzy dwoma równoległymi zastawami Ay = Bx + c1 i Ay = Bx + c2 jest dana wzorem d = |C1–C2|/√A^2 + B^2. Mając ten wzór, mamy odległość między dwoma wektorami nośnymi jako 2/||w||.

Funkcja kosztu dla SVM wygląda tak, jak poniższe równanie:

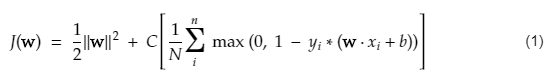
Kredyt obrazu

Funkcja utraty SVM

W powyższym równaniu funkcji kosztu parametr λ oznacza, że ​​większy λ zapewnia szerszą marżę, a mniejszy λ przyniesie mniejszą marżę. Ponadto obliczany jest gradient funkcji kosztu, a wagi są aktualizowane w kierunku, który obniża utraconą funkcję.

Przeczytaj: Algebra liniowa do uczenia maszynowego: krytyczne pojęcia, po co uczyć się przed ML

Algorytm dla nieliniowej SVM

W klasyfikatorze SVM łatwo jest mieć liniową hiperpłaszczyznę między tymi dwiema klasami. Ale pojawia się interesujące pytanie, co jeśli danych nie da się oddzielić liniowo, co należy zrobić? W tym celu algorytm SVM ma metodę nazywaną sztuczką jądra.

Funkcja jądra SVM zajmuje małowymiarową przestrzeń wejściową i konwertuje ją na przestrzeń o wyższym wymiarze. Mówiąc prościej, przekształca problem niemożliwy do rozdzielenia w problem rozdzielny. Wykonuje złożone transformacje danych na podstawie etykiet lub danych wyjściowych, które je definiują

Spójrz na poniższy diagram, aby lepiej zrozumieć transformację danych. Zestaw punktów danych po lewej stronie jest wyraźnie nierozdzielny liniowo. Ale kiedy zastosujemy funkcję Φ do zbioru punktów danych, otrzymamy przekształcone punkty danych w wyższym wymiarze, który można oddzielić za pomocą płaszczyzny.

Kredyt obrazu

Aby oddzielić nierozłączne liniowo punkty danych, musimy dodać dodatkowy wymiar. W przypadku danych liniowych zastosowano dwa wymiary, czyli x i y. Dla tych punktów danych dodajemy trzeci wymiar, powiedzmy z. Dla poniższego przykładu niech z=x² +y².

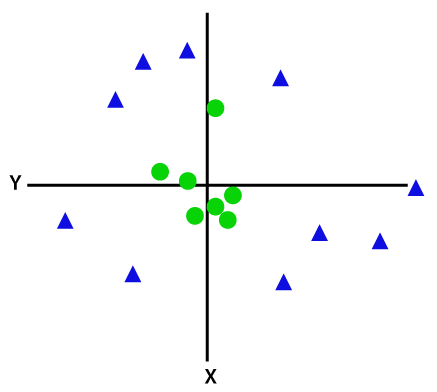
Kredyt obrazu

Ta funkcja z lub dodatkowa wymiarowość przekształca przestrzeń próbki, a powyższy obraz będzie wyglądał następująco:

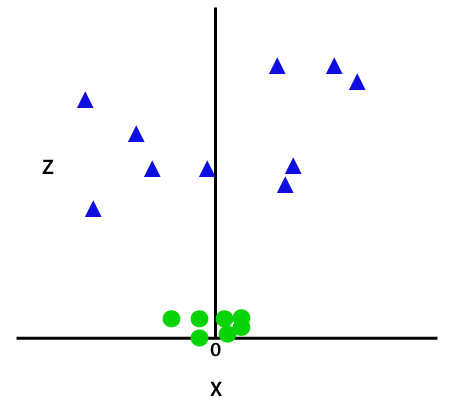
Kredyt obrazu

Po dokładnej analizie oczywiste jest, że powyższe punkty danych można oddzielić za pomocą funkcji linii prostej, która jest równoległa do osi x lub nachylona pod kątem. Istnieją różne typy funkcji jądra — liniowa, nieliniowa, wielomianowa, radialna funkcja bazowa (RBF) i sigmoidalna.

To, co robi RBF w prostych słowach, to — jeśli wybierzemy jakiś punkt, wynikiem RBF będzie norma odległości między tym punktem a pewnym stałym punktem. Innymi słowy, możemy zaprojektować wymiar az z wydajnościami tego RBF, który zazwyczaj daje „wysokość” w zależności od odległości punktu od pewnego punktu.

Sprawdź: 6 rodzajów funkcji aktywacji w sieciach neuronowych, które musisz znać

Które jądro wybrać?

Przyjemną metodą określenia, które jądro jest najbardziej odpowiednie, jest wykonanie różnych modeli z różnymi jądrami, a następnie oszacowanie każdego z ich wydajności i ostateczne porównanie wyników. Następnie wybierasz jądro z najlepszymi wynikami. Zachowaj szczególną ostrożność, aby oszacować wydajność modelu na różnych obserwacjach za pomocą walidacji krzyżowej K-Fold i weź pod uwagę różne metryki, takie jak dokładność, wynik F1 itp.

SVM w Pythonie i R

Metoda dopasowania w Pythonie po prostu trenuje model SVM na danych Xtrain i ytrain, które zostały rozdzielone. Dokładniej, metoda dopasowania zbierze dane w Xtrain i ytrain, a następnie obliczy dwa wektory wsparcia.

Po oszacowaniu tych wektorów pomocniczych model klasyfikatora jest całkowicie ustawiony na generowanie nowych prognoz z funkcją przewidywania, ponieważ potrzebuje tylko wektorów pomocniczych do oddzielenia nowych danych. Teraz możesz otrzymać różne wyniki w Pythonie i R, więc upewnij się, że sprawdziłeś wartość parametru seed.

Wniosek

W tym artykule szczegółowo przyjrzeliśmy się algorytmowi Support Vector Machine. Dziękuję za Twój czas. Oglądaj więcej takich artykułów.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.

Jakie rodzaje problemów są odpowiednie dla modeli maszyn wektorów nośnych?

Maszyny wektorów nośnych (SVM) działają najlepiej na danych, które można oddzielić liniowo, tj. danych, które można rozdzielić na dwie odrębne klasy przy użyciu linii prostej lub hiperpłaszczyzny. Jednym z najczęstszych zastosowań SVM jest rozpoznawanie twarzy. Technika eigenfaces jest przykładem SVM, która redukuje wymiarowość obrazów twarzy i jest używana do rozpoznawania twarzy. Ta technika opiera się na założeniu, że twarze można traktować jako wektory w wielowymiarowej przestrzeni wektorowej, a wymiarowość jest redukowana przez dopasowanie hipersfery do danych. Dzięki temu możemy dopasować dwie twarze, które mają inny rozmiar lub są obrócone. SVM jest również używany w klasyfikacji.

Jakie są zastosowania maszyn SVM w prawdziwym życiu?

Czy SVM może być używany do ciągłych danych?

SVM służy do tworzenia modelu klasyfikacji. Tak więc, jeśli masz klasyfikator, musi on działać tylko z dwiema klasami. Jeśli masz dane ciągłe, będziesz musiał przekształcić te dane w klasy, proces ten nazywa się redukcją wymiarowości. Na przykład, jeśli masz coś takiego jak wiek, wzrost, waga, stopień itp., możesz wziąć średnią tych danych i przybliżyć ją do jednej lub drugiej klasy, co ułatwi klasyfikację.