Máquinas de vectores de soporte: tipos de SVM [explicación del algoritmo]

Introducción

Al igual que otros algoritmos en el aprendizaje automático que realizan la tarea de clasificación (árboles de decisión, bosque aleatorio, K-NN) y regresión, Support Vector Machine o SVM es uno de esos algoritmos en todo el grupo. Es un algoritmo de aprendizaje automático supervisado (requiere conjuntos de datos etiquetados) que se utiliza para problemas relacionados con la clasificación o la regresión.

Sin embargo, se aplica con frecuencia en problemas de clasificación. El algoritmo SVM implica el trazado de cada elemento de datos como un punto. El trazado se realiza en un espacio n-dimensional donde n es el número de características de un dato en particular. Luego, la clasificación se lleva a cabo encontrando el hiperplano más adecuado que separe las dos (o más) clases de manera efectiva.

El término vectores de soporte son solo coordenadas de una característica individual. ¿Por qué generalizar los puntos de datos como vectores? En problemas del mundo real, existen conjuntos de datos de dimensiones más altas. En dimensiones más altas (dimensión n), tiene más sentido realizar manipulaciones de matriz y aritmética vectorial en lugar de considerarlas como puntos.

Tipos de MVS

SVM lineal: SVM lineal se utiliza para datos que son linealmente separables, es decir, para un conjunto de datos que se puede clasificar en dos categorías utilizando una sola línea recta. Dichos puntos de datos se denominan datos separables linealmente, y el clasificador se utiliza descrito como un clasificador SVM lineal.

SVM no lineal: SVM no lineal se usa para datos que son datos separables no linealmente, es decir, no se puede usar una línea recta para clasificar el conjunto de datos. Para esto, usamos algo conocido como truco del kernel que establece puntos de datos en una dimensión superior donde se pueden separar usando planos u otras funciones matemáticas. Dichos puntos de datos se denominan datos no lineales, y el clasificador utilizado se denomina clasificador SVM no lineal.

Algoritmo para SVM lineal

Hablemos de un problema de clasificación binaria. La tarea es clasificar eficientemente un punto de prueba en cualquiera de las clases con la mayor precisión posible. Los siguientes son los pasos involucrados en el proceso SVM.

En primer lugar, el conjunto de puntos que pertenecen a las dos clases se trazan y visualizan como se muestra a continuación. En un espacio bidimensional, con solo aplicar una línea recta, podemos dividir eficientemente estas dos clases. Pero puede haber muchas líneas que pueden clasificar estas clases. Hay un conjunto de líneas o hiperplanos (líneas verdes) para elegir. La pregunta obvia será, de todas estas líneas, ¿cuál es la adecuada para la clasificación?

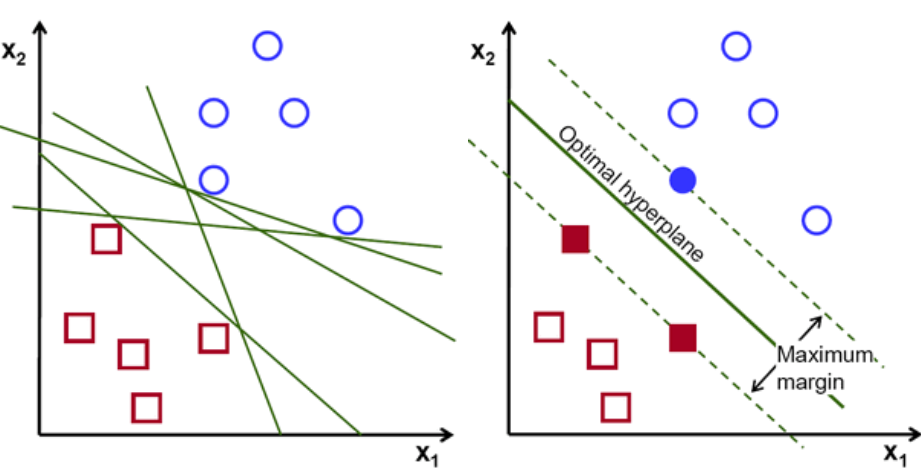
conjunto de hiperaviones, crédito de la imagen

Básicamente, seleccione el hiperplano que separa mejor las dos clases. Hacemos esto maximizando la distancia entre el punto de datos más cercano y el hiperplano. Cuanto mayor es la distancia, mejor es el hiperplano y se obtienen mejores resultados de clasificación. Se puede ver en la siguiente figura que el hiperplano seleccionado tiene la distancia máxima desde el punto más cercano de cada una de esas clases.

Un recordatorio, las dos líneas de puntos que van paralelas al hiperplano que cruzan los puntos más cercanos de cada una de las clases se denominan vectores de soporte del hiperplano. Ahora, la distancia de separación entre los vectores de apoyo y el hiperplano se llama margen. Y el propósito del algoritmo SVM es maximizar este margen. El hiperplano óptimo es el hiperplano con margen máximo.

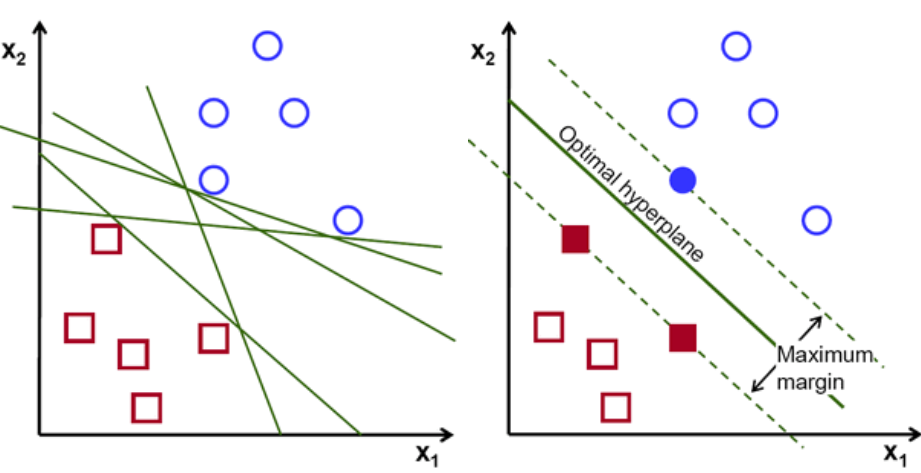
Credito de imagen

Tomemos, por ejemplo, clasificar las células como buenas y malas. la celda xᵢ se define como un Cada uno de estos vectores de características está etiquetado con una clase yᵢ. La clase yᵢ puede ser +ve o -ve (por ejemplo, bueno=1, no bueno =-1). La ecuación del hiperplano es y= wx + b = 0. Donde W y b son parámetros de línea. La ecuación anterior devuelve un valor ≥ 1 para ejemplos de clase +ve y ≤-1 para ejemplos de clase -ve.

Pero, ¿cómo encuentra este hiperplano? El hiperplano se define encontrando los valores óptimos w o pesos y b o interceptar cuál. Y estos valores óptimos se encuentran minimizando la función de costo. Una vez que el algoritmo recopila estos valores óptimos, el modelo SVM o la función de línea f(x) clasifica eficientemente las dos clases.

En pocas palabras, el hiperplano óptimo tiene la ecuación w.x+b = 0. El vector de soporte izquierdo tiene la ecuación w.x+b=-1 y el vector de soporte derecho tiene w.x+b=1.

Así, la distancia d entre dos gravámenes paralelos Ay = Bx + c1 y Ay = Bx + c2 viene dada por d = |C1–C2|/√A^2 + B^2. Con esta fórmula en su lugar, tenemos la distancia entre los dos vectores de soporte como 2/||w||.

La función de costo para SVM se parece a la siguiente ecuación:

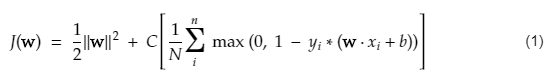
Credito de imagen

Función de pérdida de SVM

En la ecuación de la función de costo anterior, el parámetro λ denota que un λ más grande proporciona un margen más amplio, y un λ más pequeño produciría un margen más pequeño. Además, se calcula el gradiente de la función de costo y se actualizan los pesos en la dirección que baja la función perdida.

Lea: Álgebra lineal para el aprendizaje automático: conceptos críticos, por qué aprender antes de ML

Algoritmo para SVM no lineal

En el clasificador SVM, es sencillo tener un hiperplano lineal entre estas dos clases. Pero, una pregunta interesante que surge es, ¿qué pasa si los datos no son linealmente separables, qué se debe hacer? Para esto, el algoritmo SVM tiene un método llamado kernel trick.

La función kernel SVM toma un espacio de entrada de baja dimensión y lo convierte en un espacio de mayor dimensión. En palabras simples, convierte el problema no separable en un problema separable. Realiza transformaciones de datos complejas en base a las etiquetas o salidas que los definen.

Mire el siguiente diagrama para comprender mejor la transformación de datos. El conjunto de puntos de datos de la izquierda claramente no son linealmente separables. Pero cuando aplicamos una función Φ al conjunto de puntos de datos, obtenemos puntos de datos transformados en una dimensión superior que es separable a través de un plano.

Credito de imagen

Para separar puntos de datos separables no linealmente, debemos agregar una dimensión adicional. Para datos lineales se han utilizado dos dimensiones, es decir, x e y. Para estos puntos de datos, agregamos una tercera dimensión, digamos z. Para el siguiente ejemplo, sea z=x² +y².

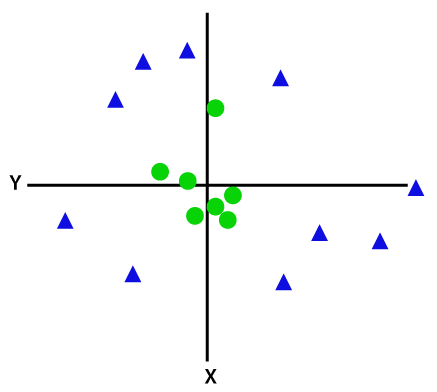
Credito de imagen

Esta función z o la dimensionalidad agregada transforma el espacio de muestra y la imagen de arriba se convertirá en la siguiente:

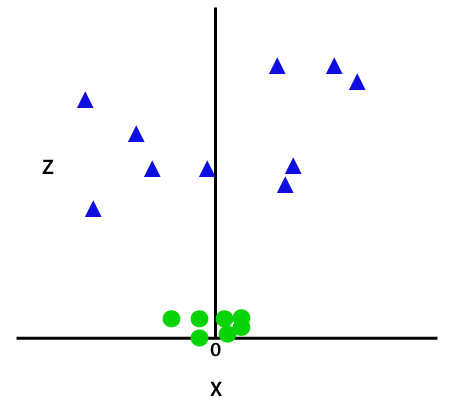
Credito de imagen

En un análisis detallado, es evidente que los puntos de datos anteriores se pueden separar utilizando una función de línea recta que es paralela al eje x o está inclinada en ángulo. Están presentes diferentes tipos de funciones kernel: lineal, no lineal, polinómica, función de base radial (RBF) y sigmoidea.

Lo que hace RBF en palabras simples es: si elegimos algún punto, el resultado de un RBF será la norma de la distancia entre ese punto y algún punto fijo. En otras palabras, podemos diseñar una dimensión z con los rendimientos de este RBF, que normalmente da 'altura' dependiendo de qué tan lejos esté el punto de algún punto.

Consulte: 6 tipos de funciones de activación en redes neuronales que debe conocer

¿Qué núcleo elegir?

Un buen método para determinar qué kernel es el más adecuado es hacer varios modelos con diferentes kernels, luego estimar cada uno de sus rendimientos y, en última instancia, comparar los resultados. Luego elige el núcleo con los mejores resultados. Sea particular al estimar el rendimiento del modelo en observaciones diferentes mediante el uso de validación cruzada K-Fold y considere diferentes métricas como precisión, puntaje F1, etc.

SVM en Python y R

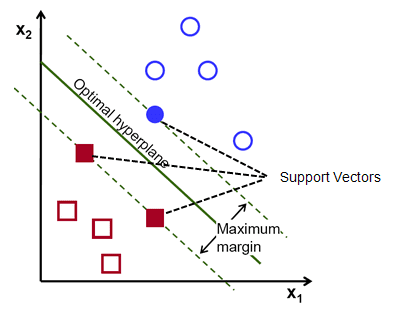
El método de ajuste en python simplemente entrena el modelo SVM en los datos de Xtrain e ytrain que se han separado. Más específicamente, el método de ajuste ensamblará los datos en Xtrain e ytrain y, a partir de ahí, calculará los dos vectores de soporte.

Una vez que se estiman estos vectores de soporte, el modelo clasificador está completamente configurado para producir nuevas predicciones con la función de predicción porque solo necesita los vectores de soporte para separar los nuevos datos. Ahora puede obtener resultados diferentes en Python y en R, así que asegúrese de verificar el valor del parámetro semilla.

Conclusión

En este artículo, analizamos en detalle el algoritmo de la máquina de vectores de soporte. Gracias por tu tiempo. Sintonice para más artículos de este tipo.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.

¿Para qué tipo de problemas son buenos los modelos Support Vector Machine?

Las máquinas de vectores de soporte (SVM) funcionan mejor con datos linealmente separables, es decir, datos que se pueden separar en dos clases distintas utilizando una línea recta o un hiperplano. Uno de los usos más comunes de SVM es el reconocimiento facial. La técnica de caras propias es un ejemplo de SVM, que reduce la dimensionalidad de las imágenes faciales y se utiliza para el reconocimiento facial. Esta técnica se basa en la premisa de que las caras se pueden considerar como vectores en un espacio vectorial de alta dimensión y la dimensionalidad se reduce ajustando una hiperesfera a los datos. Esto nos permite hacer coincidir dos caras que tienen un tamaño diferente o están rotadas. SVM también se utiliza en la clasificación.

¿Cuáles son las aplicaciones de las SVM en la vida real?

¿Se puede usar SVM para datos continuos?

SVM se utiliza para crear un modelo de clasificación. Entonces, si tiene un clasificador, debe funcionar con solo dos clases. Si tiene datos continuos, tendrá que convertir esos datos en clases, el proceso se llama reducción de dimensionalidad. Por ejemplo, si tiene algo como la edad, la altura, el peso, el grado, etc., puede tomar la media de esos datos y acercarlos a una clase u otra, lo que facilitará la clasificación.