Destek Vektör Makineleri: SVM Türleri [Algoritma Açıklaması]

Tanıtım

Tıpkı tüm havuzda sınıflandırma (karar ağaçları, rastgele orman, K-NN) ve regresyon, Destek Vektör Makinesi veya SVM görevini yerine getiren makine öğrenimindeki diğer algoritmalar gibi. Sınıflandırma veya regresyonla ilgili problemler için kullanılan denetimli (etiketli veri kümeleri gerektirir) bir makine öğrenme algoritmasıdır.

Ancak sınıflandırma problemlerinde sıklıkla uygulanmaktadır. SVM algoritması, her veri öğesinin bir nokta olarak çizilmesini gerektirir. Çizim, n'nin belirli bir verinin özelliklerinin sayısı olduğu n-boyutlu bir uzayda yapılır. Daha sonra iki (veya daha fazla) sınıfı etkin bir şekilde ayıran en uygun hiperdüzlem bulunarak sınıflandırma yapılır.

Destek vektörleri terimi sadece tek bir özelliğin koordinatlarıdır. Veri noktalarını neden vektörler olarak genelleştirelim? Gerçek dünya problemlerinde, daha yüksek boyutlarda veri kümeleri vardır. Daha yüksek boyutlarda(n-boyut), vektör aritmetiği ve matris işlemlerini nokta olarak görmektense yapmak daha mantıklıdır.

SVM Türleri

Doğrusal SVM : Doğrusal SVM, doğrusal olarak ayrılabilen veriler için, yani tek bir düz çizgi kullanılarak iki kategoriye ayrılabilen bir veri kümesi için kullanılır. Bu tür veri noktaları, doğrusal olarak ayrılabilir veriler olarak adlandırılır ve sınıflandırıcı, bir Doğrusal SVM sınıflandırıcısı olarak tanımlanan şekilde kullanılır.

Doğrusal Olmayan SVM: Doğrusal Olmayan SVM, doğrusal olarak ayrılamayan veriler olan veriler için kullanılır, yani veri kümesini sınıflandırmak için düz bir çizgi kullanılamaz. Bunun için, veri noktalarını düzlemler veya diğer matematiksel işlevler kullanılarak ayrılabilecekleri daha yüksek bir boyuta ayarlayan çekirdek hilesi olarak bilinen bir şey kullanıyoruz. Bu tür veri noktaları, doğrusal olmayan veriler olarak adlandırılır ve kullanılan sınıflandırıcı, Doğrusal Olmayan SVM sınıflandırıcı olarak adlandırılır.

Doğrusal SVM için Algoritma

Bir ikili sınıflandırma probleminden bahsedelim. Görev, herhangi bir sınıftaki bir test noktasını mümkün olduğunca doğru bir şekilde verimli bir şekilde sınıflandırmaktır. Aşağıda, SVM sürecinde yer alan adımlar yer almaktadır.

İlk olarak, iki sınıfa ait nokta kümeleri çizilir ve aşağıda gösterildiği gibi görselleştirilir. 2 boyutlu uzayda sadece düz bir çizgi uygulayarak bu iki sınıfı verimli bir şekilde bölebiliriz. Fakat bu sınıfları sınıflandırabilecek birçok satır olabilir. Aralarından seçim yapabileceğiniz bir dizi çizgi veya hiper düzlem (yeşil çizgiler) vardır. Açık soru, tüm bu satırlardan hangi satırın sınıflandırmaya uygun olduğu olacaktır.

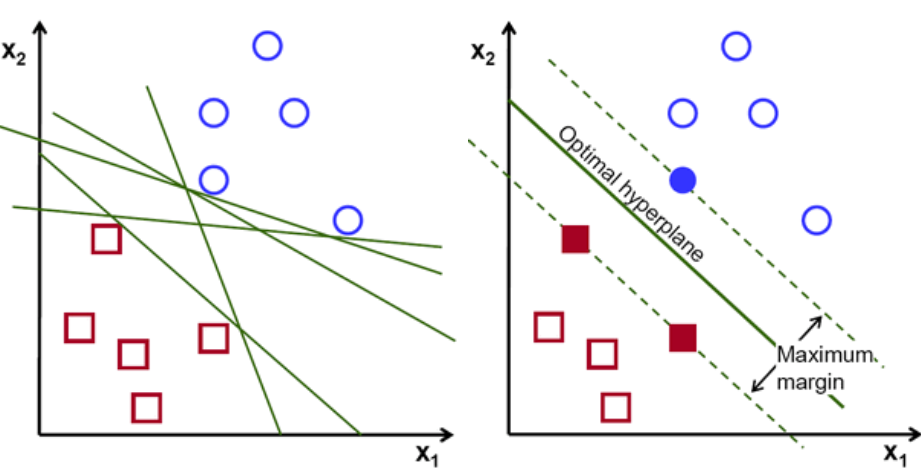
hiper düzlemler seti, Görüntü kredisi

Temel olarak, iki sınıfı daha iyi ayıran hiper düzlemi seçin. Bunu, en yakın veri noktası ile hiper-düzlem arasındaki mesafeyi maksimize ederek yapıyoruz. Mesafe ne kadar büyükse, hiperdüzlem o kadar iyidir ve daha iyi sınıflandırma sonuçları ortaya çıkar. Aşağıdaki şekilde, seçilen hiperdüzlemin, bu sınıfların her birinden en yakın noktadan maksimum uzaklığa sahip olduğu görülebilir.

Bir hatırlatıcı olarak, sınıfların her birinin en yakın noktalarından geçen hiperdüzleme paralel giden iki noktalı çizgi, hiperdüzlemin destek vektörleri olarak adlandırılır. Destekleyici vektörler ile hiperdüzlem arasındaki mesafeye marj denir. Ve SVM algoritmasının amacı bu marjı maksimize etmektir. Optimal hiperdüzlem, maksimum marjı olan hiperdüzlemdir.

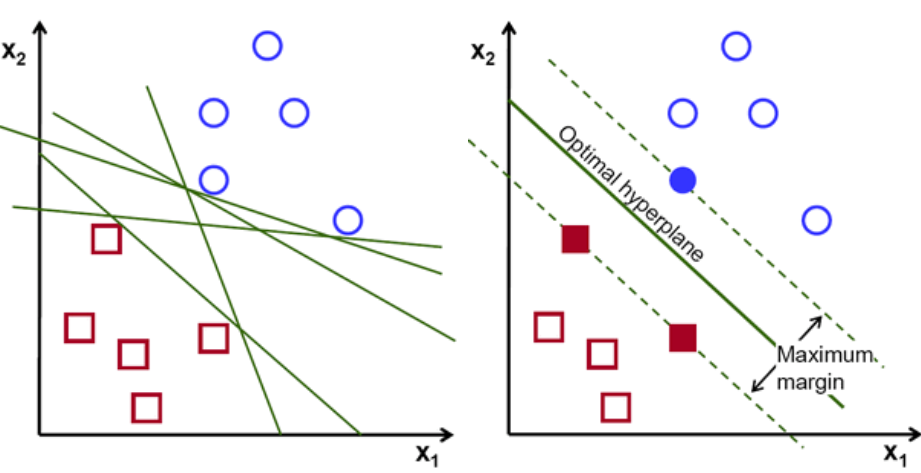
Resim kredisi

Örneğin, hücreleri iyi ve kötü olarak sınıflandırmayı ele alalım. xᵢ hücresi , n-boyutlu uzayda çizilebilen Bu özellik vektörlerinin her biri bir yᵢ sınıfı ile etiketlenmiştir. yᵢ sınıfı +ve veya -ve olabilir (örn. iyi=1, iyi değil =-1). Hiper düzlemin denklemi y= wx + b = 0'dır. Burada W ve b çizgi parametreleridir. Önceki denklem , +ve sınıfı örnekleri için ≥ 1 ve -ve sınıfı örnekleri için ≤-1 değerini döndürür.

Peki ama bu hiper düzlemi nasıl buluyor? Hiper düzlem, w veya ağırlıklar ve b veya kesişen optimal değerlerin bulunmasıyla tanımlanır. Ve bu optimal değerler, maliyet fonksiyonunun minimize edilmesiyle bulunur. Algoritma bu optimal değerleri topladıktan sonra, SVM modeli veya hat fonksiyonu f(x) iki sınıfı verimli bir şekilde sınıflandırır.

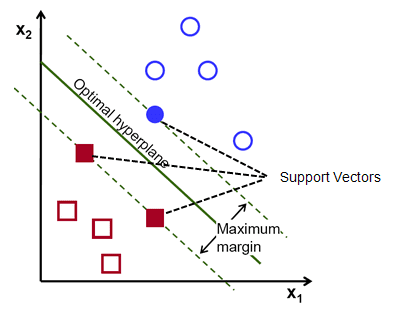
Özetle, optimal hiperdüzlem w.x+b = 0 denklemine sahiptir. Sol destek vektörü w.x+b=-1 ve sağ destek vektörü w.x+b=1 denklemine sahiptir.

Böylece iki paralel haciz Ay = Bx + c1 ve Ay = Bx + c2 arasındaki d mesafesi d = |C1–C2|/√A^2 + B^2 ile verilir. Bu formül yerindeyken, iki destek vektörü arasındaki mesafeyi 2/||w|| olarak elde ederiz.

SVM için maliyet fonksiyonu aşağıdaki denkleme benzer:

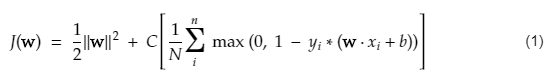
Resim kredisi

SVM kayıp fonksiyonu

Yukarıdaki maliyet fonksiyonu denkleminde, λ parametresi, daha büyük bir λ'nın daha geniş bir marj sağladığını ve daha küçük bir λ'nın daha küçük bir marj sağlayacağını belirtir. Ayrıca, maliyet fonksiyonunun gradyanı hesaplanır ve ağırlıklar, kayıp fonksiyonu düşüren yönde güncellenir.

Okuyun: Makine Öğrenimi için Lineer Cebir: Kritik Kavramlar, Neden Makine Öğrenimi Öncesi Öğrenilir

Doğrusal Olmayan SVM için Algoritma

DVM sınıflandırıcısında, bu iki sınıf arasında doğrusal bir hiper düzleme sahip olmak basittir. Ancak ortaya çıkan ilginç bir soru, veriler doğrusal olarak ayrılabilir değilse ne yapılmalı? Bunun için SVM algoritmasının kernel trick adlı bir metodu vardır.

SVM çekirdek işlevi, düşük boyutlu girdi uzayını alır ve onu daha yüksek boyutlu bir uzaya dönüştürür. Basit bir deyişle, ayrılamayan sorunu ayrılabilir bir soruna dönüştürür. Bunları tanımlayan etiketlere veya çıktılara dayalı olarak karmaşık veri dönüşümleri gerçekleştirir.

Veri dönüşümünü daha iyi anlamak için aşağıdaki şemaya bakın. Soldaki veri noktaları kümesi açıkça doğrusal olarak ayrılamaz. Ancak veri noktaları kümesine bir fonksiyon uyguladığımızda, bir düzlem aracılığıyla ayrılabilen daha yüksek bir boyutta dönüştürülmüş veri noktaları elde ederiz.

Resim kredisi

Doğrusal olarak ayrılamayan veri noktalarını ayırmak için fazladan bir boyut eklemeliyiz. Doğrusal veriler için iki boyut, yani x ve y kullanılmıştır. Bu veri noktaları için üçüncü bir boyut ekliyoruz, diyelim ki z. Aşağıdaki örnek için z=x² +y² olsun.

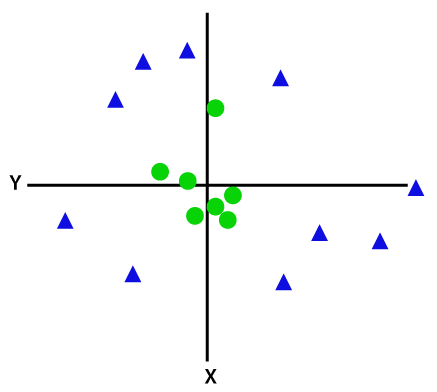
Resim kredisi

Bu z işlevi veya eklenen boyut, örnek uzayı dönüştürür ve yukarıdaki görüntü aşağıdaki gibi olur:

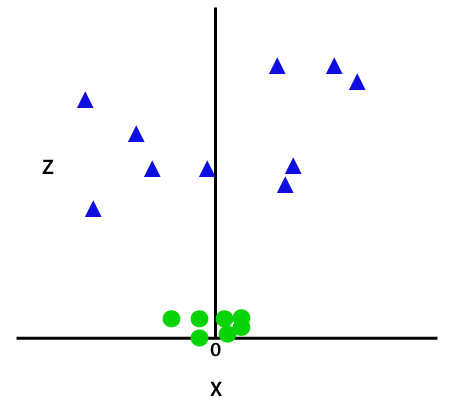
Resim kredisi

Yakın analizde, yukarıdaki veri noktalarının, ya x eksenine paralel olan ya da bir açıyla eğimli olan bir düz çizgi işlevi kullanılarak ayrılabileceği açıktır. Farklı tipte çekirdek fonksiyonları mevcuttur - doğrusal, doğrusal olmayan, polinom, radyal temel fonksiyon (RBF) ve sigmoid.

RBF'nin basit kelimelerle yaptığı şey şudur - bir nokta seçersek, bir RBF'nin sonucu o nokta ile sabit bir nokta arasındaki mesafenin normu olacaktır. Başka bir deyişle, noktanın bir noktadan ne kadar uzak olduğuna bağlı olarak tipik olarak 'yükseklik' veren bu RBF'nin verimleriyle az boyutunu tasarlayabiliriz.

Bakın : Sinir Ağlarında Bilmeniz Gereken 6 Tip Aktivasyon Fonksiyonu

Hangi Çekirdeği seçmeli?

Hangi çekirdeğin en uygun olduğunu belirlemenin güzel bir yöntemi, farklı çekirdeklerle çeşitli modeller yapmak, ardından her birinin performansını tahmin etmek ve nihayetinde sonuçları karşılaştırmaktır. Sonra en iyi sonucu veren çekirdeği seçersiniz. Modelin performansını K-Fold Çapraz Doğrulamayı kullanarak farklı gözlemlerde tahmin etmeye özen gösterin ve Doğruluk, F1 Skoru vb. gibi farklı metrikleri göz önünde bulundurun.

Python ve R'de SVM

Python'daki fit yöntemi, SVM modelini ayrılmış Xtrain ve ytrain verileri üzerinde eğitir. Daha spesifik olarak, fit yöntemi, verileri Xtrain ve ytrain'de bir araya getirecek ve bundan iki destek vektörünü hesaplayacaktır.

Bu destek vektörleri tahmin edildiğinde, sınıflandırıcı model tamamen yeni verileri ayırmak için destek vektörlerine ihtiyaç duyduğu için tahmin işleviyle yeni tahminler üretecek şekilde ayarlanır. Şimdi Python ve R'de farklı sonuçlar alabilirsiniz, bu nedenle tohum parametresinin değerini kontrol ettiğinizden emin olun.

Çözüm

Bu yazımızda Support Vector Machine algoritmasını detaylı olarak inceledik. Zaman ayırdığınız için teşekkürler. Daha fazla bu tür makaleler için takip edin.

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.

Destek Vektör Makinesi modelleri ne tür sorunlara iyi gelir?

Destek Vektör Makineleri (SVM) en iyi şekilde doğrusal olarak ayrılabilir veriler üzerinde çalışır, yani düz bir çizgi veya hiperdüzlem kullanılarak iki farklı sınıfa ayrılabilen veriler. SVM'nin en yaygın kullanımlarından biri yüz tanımadır. Özyüzler tekniği, yüz görüntülerinin boyutsallığını azaltan ve yüz tanıma için kullanılan bir SVM örneğidir. Bu teknik, yüzlerin yüksek boyutlu bir vektör uzayında vektörler olarak düşünülebileceği ve verilere bir hiper küre uydurularak boyutluluğun azaltılabileceği öncülüne dayanmaktadır. Bu, farklı boyuttaki veya döndürülmüş iki yüzü eşleştirmemizi sağlar. Sınıflandırmada SVM de kullanılır.

SVM'lerin gerçek hayattaki uygulamaları nelerdir?

Sürekli veri için SVM kullanılabilir mi?

SVM, bir sınıflandırma modeli oluşturmak için kullanılır. Yani bir sınıflandırıcınız varsa, sadece iki sınıfla çalışması gerekir. Sürekli verileriniz varsa, o zaman bu verileri sınıflara dönüştürmeniz gerekecek, işleme boyutsallık azaltma denir. Örneğin, yaş, boy, kilo, sınıf vb. gibi bir şeye sahipseniz, bu verilerin ortalamasını alabilir ve onu bir sınıfa veya diğerine daha yakın hale getirebilirsiniz, bu da sınıflandırmayı kolaylaştıracaktır.