Mașini de suport Vector: Tipuri de SVM [Algoritm explicat]

Introducere

La fel ca alți algoritmi din învățarea automată care îndeplinesc sarcina de clasificare (arbori de decizie, pădure aleatoare, K-NN) și regresie, Support Vector Machine sau SVM un astfel de algoritm în întregul pool. Este un algoritm de învățare automată supravegheat (necesită seturi de date etichetate) care este utilizat pentru probleme legate fie de clasificare, fie de regresie.

Cu toate acestea, se aplică frecvent în probleme de clasificare. Algoritmul SVM presupune reprezentarea grafică a fiecărui element de date ca punct. Trasarea se face într-un spațiu n-dimensional unde n este numărul de caracteristici ale unei anumite date. Apoi, clasificarea este efectuată prin găsirea celui mai potrivit hiperplan care separă efectiv cele două (sau mai multe) clase.

Termenul vectori suport sunt doar coordonatele unei caracteristici individuale. De ce să generalizați punctele de date ca vectori vă puteți întreba. În problemele din lumea reală, există seturi de date de dimensiuni mai mari. În dimensiuni mai mari (n-dimensiune), este mai logic să efectuați aritmetică vectorială și manipulări matrice, decât să le considerați puncte.

Tipuri de SVM

Linear SVM: Linear SVM este utilizat pentru date care sunt separabile liniar, adică pentru un set de date care poate fi clasificat în două categorii utilizând o singură linie dreaptă. Astfel de puncte de date sunt denumite date liniar separabile, iar clasificatorul este folosit descris ca un clasificator liniar SVM.

SVM non-liniar: SVM non-liniar este utilizat pentru date care sunt date ne-liniar separabile, adică o linie dreaptă nu poate fi utilizată pentru a clasifica setul de date. Pentru aceasta, folosim ceva cunoscut ca un truc al nucleului care setează puncte de date într-o dimensiune superioară, unde pot fi separate folosind planuri sau alte funcții matematice. Astfel de puncte de date sunt denumite date neliniare, iar clasificatorul utilizat este denumit clasificator SVM neliniar.

Algoritm pentru SVM liniar

Să vorbim despre o problemă de clasificare binară. Sarcina este de a clasifica eficient un punct de testare în oricare dintre clase cât mai precis posibil. Mai jos sunt pașii implicați în procesul SVM.

În primul rând, un set de puncte aparținând celor două clase sunt reprezentate și vizualizate așa cum se arată mai jos. Într-un spațiu 2-d prin simpla aplicare a unei linii drepte, putem împărți eficient aceste două clase. Dar pot exista multe linii care pot clasifica aceste clase. Există un set de linii sau hiperplane (linii verzi) din care să alegeți. Întrebarea evidentă va fi, dintre toate aceste rânduri, care linie este potrivită pentru clasificare?

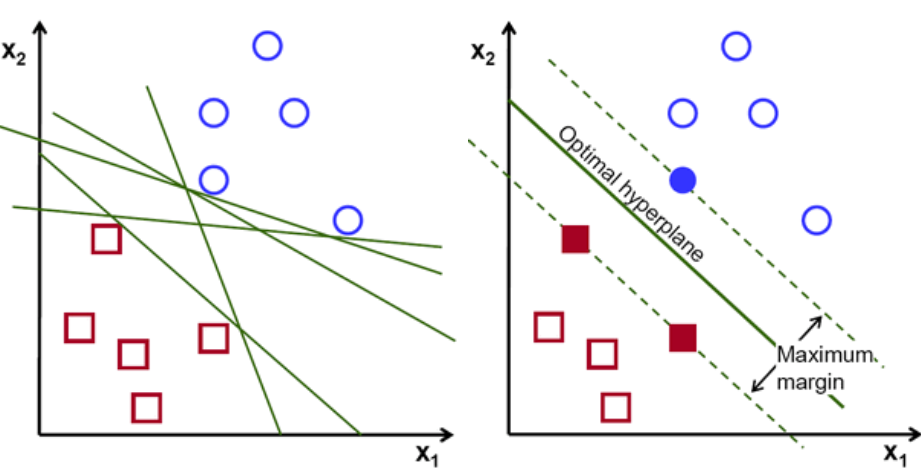
set de hiper-planuri, credit imagine

Practic, Selectați hiperplanul care separă mai bine cele două clase. Facem acest lucru prin maximizarea distanței dintre cel mai apropiat punct de date și hiperplan. Cu cât distanța este mai mare, cu atât hiperplanul este mai bun și rezultă rezultate mai bune de clasificare. Se poate observa în figura de mai jos că hiperplanul selectat are distanța maximă de la cel mai apropiat punct din fiecare dintre acele clase.

O reamintire, cele două linii punctate care merg paralele cu hiperplanul traversând cele mai apropiate puncte ale fiecărei clase sunt denumite vectori suport ai hiperplanului. Acum, distanța de separare dintre vectorii de susținere și hiperplan se numește marjă. Și scopul algoritmului SVM este de a maximiza această marjă. Hiperplanul optim este hiperplanul cu margine maximă.

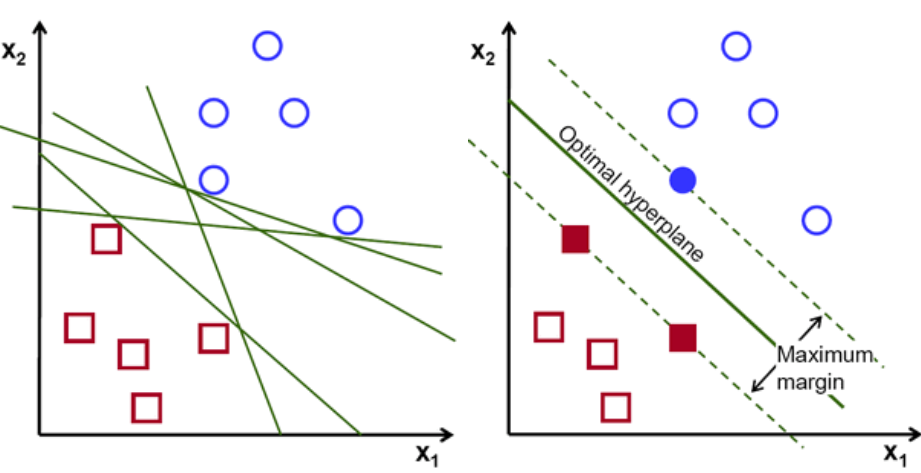
Credit imagine

Luați de exemplu clasificarea celulelor ca bune și rele. celula xᵢ este definită ca un Fiecare dintre acești vectori caracteristici este etichetat cu o clasă yᵢ. Clasa yᵢ poate fi fie +ve, fie -ve (de ex. bun=1, nu bun =-1). Ecuația hiperplanului este y= wx + b = 0. Unde W și b sunt parametri de linie. Ecuația anterioară returnează o valoare ≥ 1 pentru exemple pentru clasa +ve și ≤-1 pentru exemple de clasă -ve.

Dar, cum găsește acest hiperplan? Hiperplanul este definit prin găsirea valorilor optime w sau ponderi și b sau interceptare care. Și aceste valori optime se găsesc prin minimizarea funcției de cost. Odată ce algoritmul colectează aceste valori optime, modelul SVM sau funcția linie f(x) clasifică eficient cele două clase.

Pe scurt, hiperplanul optim are ecuația w.x+b = 0. Vectorul suport din stânga are ecuația w.x+b=-1, iar vectorul suport din dreapta are w.x+b=1.

Astfel, distanța d dintre două drepturi paralele Ay = Bx + c1 și Ay = Bx + c2 este dată de d = |C1–C2|/√A^2 + B^2. Cu această formulă în loc, avem distanța dintre cei doi vectori suport ca 2/||w||.

Funcția de cost pentru SVM arată ca ecuația de mai jos:

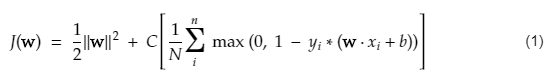
Credit imagine

Funcția de pierdere SVM

În ecuația funcției de cost de mai sus, parametrul λ indică faptul că un λ mai mare oferă o marjă mai largă, iar un λ mai mic ar produce o marjă mai mică. Mai mult, se calculează gradientul funcției de cost și ponderile sunt actualizate în direcția care scade funcția pierdută.

Citiți: Algebră liniară pentru învățarea automată: concepte critice, de ce să învățați înainte de ML

Algoritm pentru SVM neliniar

În clasificatorul SVM, este simplu să existe un hiperplan liniar între aceste două clase. Dar, o întrebare interesantă care apare este: ce ar trebui făcut dacă datele nu sunt separabile liniar? Pentru aceasta, algoritmul SVM are o metodă numită trucul nucleului.

Funcția de nucleu SVM preia spațiu de intrare cu dimensiuni reduse și îl convertește într-un spațiu de dimensiuni mai mari. Cu cuvinte simple, transformă problema neseparabilă într-o problemă separabilă. Efectuează transformări complexe de date pe baza etichetelor sau ieșirilor care le definesc

Priviți diagrama de mai jos pentru a înțelege mai bine transformarea datelor. Setul de puncte de date din stânga nu este în mod clar separabil liniar. Dar când aplicăm o funcție Φ setului de puncte de date, obținem puncte de date transformate într-o dimensiune superioară care este separabilă printr-un plan.

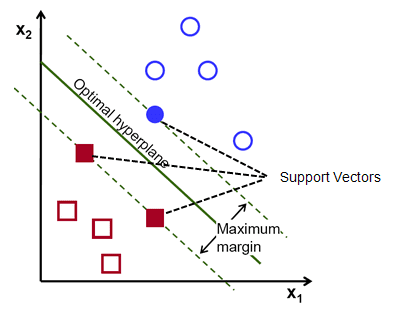
Credit imagine

Pentru a separa punctele de date neseparabile liniar, trebuie să adăugăm o dimensiune suplimentară. Pentru datele liniare s-au folosit două dimensiuni, adică x și y. Pentru aceste puncte de date, adăugăm o a treia dimensiune, să spunem z. Pentru exemplul de mai jos, fie z=x² +y².

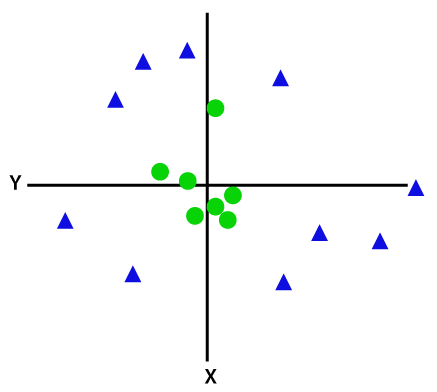
Credit imagine

Această funcție z sau dimensionalitatea adăugată transformă spațiul eșantion și imaginea de mai sus va deveni după cum urmează:

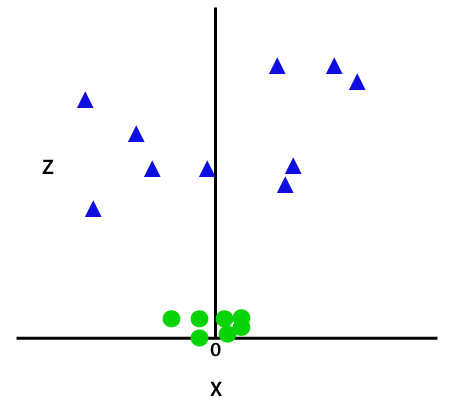
Credit imagine

La o analiză atentă, este evident că punctele de date de mai sus pot fi separate folosind o funcție de linie dreaptă care este fie paralelă cu axa x, fie este înclinată la un unghi. Sunt prezente diferite tipuri de funcții nucleu - liniare, neliniare, polinomiale, funcție de bază radială (RBF) și sigmoid.

Ceea ce face RBF în cuvinte simple este: dacă alegem un punct, rezultatul unui RBF va fi norma distanței dintre acel punct și un punct fix. Cu alte cuvinte, putem proiecta dimensiunea az cu randamentele acestui RBF, care de obicei dă „înălțime” în funcție de cât de departe este punctul de un punct.

Verificați: 6 tipuri de funcție de activare în rețelele neuronale pe care trebuie să le cunoașteți

Ce kernel să alegi?

O metodă bună de a determina care nucleu este cel mai potrivit este de a realiza diverse modele cu nuclee diferite, apoi de a estima performanța fiecăruia și, în cele din urmă, de a compara rezultatele. Apoi alegeți nucleul cu cele mai bune rezultate. Fiți special pentru a estima performanța modelului pe observații diferite, utilizând validarea încrucișată în K-Fold și luați în considerare diferite valori precum Acuratețea, Scorul F1 etc.

SVM în Python și R

Metoda de potrivire din python antrenează pur și simplu modelul SVM pe datele Xtrain și ytrain care au fost separate. Mai precis, metoda fit va asambla datele în Xtrain și ytrain și, din aceasta, va calcula cei doi vectori suport.

Odată ce acești vectori suport sunt estimați, modelul de clasificator este complet setat pentru a produce noi predicții cu funcția de predicție, deoarece are nevoie doar de vectorii de suport pentru a separa noile date. Acum este posibil să obțineți rezultate diferite în Python și în R, așa că asigurați-vă că verificați valoarea parametrului seed.

Concluzie

În acest articol, ne-am uitat la algoritmul Support Vector Machine în detaliu. Mulțumesc pentru timpul acordat. Conectați-vă pentru mai multe astfel de articole.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT- B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.

Pentru ce tipuri de probleme sunt bune modelele Support Vector Machine?

Support Vector Machines (SVM) funcționează cel mai bine pe date liniar separabile, adică date care pot fi separate în două clase distincte folosind o linie dreaptă sau un hiperplan. Una dintre cele mai frecvente utilizări ale SVM este recunoașterea feței. Tehnica eigenfaces este un exemplu de SVM, care reduce dimensionalitatea imaginilor faciale și este utilizată pentru recunoașterea feței. Această tehnică se bazează pe premisa că fețele pot fi gândite ca vectori într-un spațiu vectorial de dimensiuni mari, iar dimensionalitatea este redusă prin potrivirea unei hipersfere la date. Acest lucru ne permite să potrivim două fețe care au o dimensiune diferită sau sunt rotite. SVM este, de asemenea, utilizat în clasificare.

Care sunt aplicațiile SVM-urilor în viața reală?

Poate fi folosit SVM pentru date continue?

SVM este folosit pentru a crea un model de clasificare. Deci, dacă aveți un clasificator, acesta trebuie să funcționeze doar cu două clase. Dacă aveți date continue, atunci va trebui să transformați acele date în clase, procesul se numește reducerea dimensionalității. De exemplu, dacă aveți ceva precum vârsta, înălțimea, greutatea, nota etc., atunci puteți lua media acestor date și o puteți apropia de o clasă sau de alta, ceea ce va ușura apoi clasificarea.