รองรับ Vector Machines: ประเภทของ SVM [อธิบายอัลกอริทึม]

บทนำ

เช่นเดียวกับอัลกอริทึมอื่นๆ ในแมชชีนเลิร์นนิงที่ทำงานในการจัดหมวดหมู่ (แผนผังการตัดสินใจ, ฟอเรสต์สุ่ม, K-NN) และการถดถอย, รองรับ Vector Machine หรือ SVM หนึ่งในอัลกอริธึมดังกล่าวในพูลทั้งหมด เป็นอัลกอริธึมการเรียนรู้ของเครื่อง (ต้องมีป้ายกำกับ) ภายใต้การดูแลที่ใช้สำหรับปัญหาที่เกี่ยวข้องกับการจำแนกประเภทหรือการถดถอย

อย่างไรก็ตาม มักใช้ในปัญหาการจำแนกประเภท อัลกอริธึม SVM เกี่ยวข้องกับการพล็อตของแต่ละรายการข้อมูลเป็นจุด การพล็อตจะทำในพื้นที่ n มิติ โดยที่ n คือจำนวนคุณลักษณะของข้อมูลเฉพาะ จากนั้น การจัดประเภทจะดำเนินการโดยการค้นหาไฮเปอร์เพลนที่เหมาะสมที่สุดที่แยกสองคลาส (หรือมากกว่า) ออกจากกันอย่างมีประสิทธิภาพ

ระยะสนับสนุนเวกเตอร์เป็นเพียงพิกัดของแต่ละคุณลักษณะ เหตุใดจึงสรุปจุดข้อมูลเป็นเวกเตอร์ที่คุณอาจถาม ในปัญหาในโลกแห่งความเป็นจริง มีชุดข้อมูลของมิติที่สูงกว่า ในมิติที่สูงกว่า (n-dimension) มันสมเหตุสมผลกว่าที่จะทำการคำนวณเวกเตอร์และการจัดการเมทริกซ์มากกว่าที่จะพิจารณาพวกมันเป็นจุด

ประเภทของ SVM

Linear SVM : Linear SVM ใช้สำหรับข้อมูลที่แยกเชิงเส้นได้ เช่น สำหรับชุดข้อมูลที่สามารถแบ่งออกเป็นสองประเภทโดยใช้เส้นตรงเส้นเดียว จุดข้อมูลดังกล่าวเรียกว่าข้อมูลที่แยกออกได้เชิงเส้น และมีการใช้ตัวแยกประเภทเป็นตัวแยกประเภท SVM เชิงเส้น

Non-linear SVM: Non-Linear SVM ใช้สำหรับข้อมูลที่เป็นข้อมูลที่ไม่สามารถแยกเป็นเส้นตรงได้ เช่น ไม่สามารถใช้เส้นตรงเพื่อจำแนกชุดข้อมูลได้ สำหรับสิ่งนี้ เราใช้สิ่งที่เรียกว่าเคล็ดลับเคอร์เนลที่กำหนดจุดข้อมูลในมิติที่สูงขึ้น โดยสามารถแยกพวกมันออกโดยใช้ระนาบหรือฟังก์ชันทางคณิตศาสตร์อื่นๆ จุดข้อมูลดังกล่าวเรียกว่าข้อมูลแบบไม่เชิงเส้น และตัวแยกประเภทที่ใช้เรียกว่าตัวแยกประเภท SVM แบบไม่เชิงเส้น

อัลกอริทึมสำหรับ Linear SVM

มาพูดถึงปัญหาการจำแนกเลขฐานสองกัน ภารกิจคือการจัดประเภทจุดทดสอบอย่างมีประสิทธิภาพในคลาสใดคลาสหนึ่งอย่างถูกต้องที่สุด ต่อไปนี้เป็นขั้นตอนที่เกี่ยวข้องในกระบวนการ SVM

ประการแรก ชุดของคะแนนที่เป็นของทั้งสองคลาสจะถูกวางแผนและแสดงเป็นภาพดังที่แสดงด้านล่าง ในพื้นที่ 2 มิติโดยการใช้เส้นตรง เราก็สามารถแบ่งคลาสทั้งสองนี้ได้อย่างมีประสิทธิภาพ แต่มีหลายบรรทัดที่สามารถจำแนกคลาสเหล่านี้ได้ มีชุดเส้นหรือไฮเปอร์เพลน (เส้นสีเขียว) ให้เลือก คำถามที่ชัดเจนคือ จากบรรทัดเหล่านี้ทั้งหมด แนวใดที่เหมาะสำหรับการจัดหมวดหมู่?

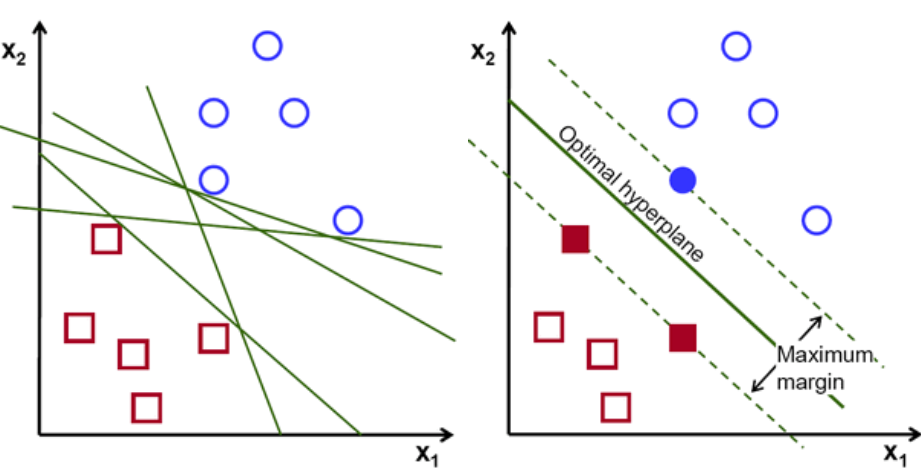
ชุดไฮเปอร์เพลน เครดิตรูปภาพ

โดยพื้นฐานแล้ว เลือกไฮเปอร์เพลนที่แยกสองคลาสได้ดีกว่า เราทำสิ่งนี้โดยเพิ่มระยะห่างระหว่างจุดข้อมูลที่ใกล้ที่สุดกับระนาบไฮเปอร์ ยิ่งระยะทางไกลเท่าไร ไฮเปอร์เพลนก็จะยิ่งดีขึ้นและผลการจัดหมวดหมู่ก็จะดีขึ้น ดังรูปด้านล่างว่าไฮเปอร์เพลนที่เลือกมีระยะห่างสูงสุดจากจุดที่ใกล้ที่สุดจากแต่ละคลาสเหล่านั้น

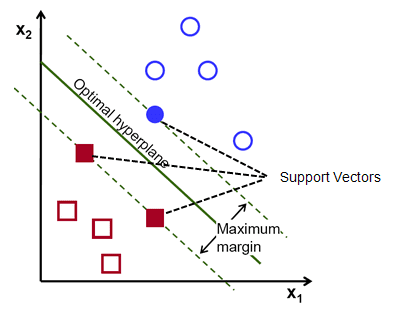
ข้อควรจำ เส้นประสองเส้นที่ขนานกับไฮเปอร์เพลนที่ตัดผ่านจุดที่ใกล้ที่สุดของแต่ละคลาสจะเรียกว่าเวกเตอร์สนับสนุนของไฮเปอร์เพลน ทีนี้ ระยะห่างระหว่างเวกเตอร์ที่รองรับกับไฮเปอร์เพลนเรียกว่าระยะขอบ และจุดประสงค์ของอัลกอริธึม SVM คือการเพิ่มมาร์จิ้นนี้ให้สูงสุด ไฮเปอร์เพลนที่เหมาะสมที่สุดคือไฮเปอร์เพลนที่มีระยะขอบสูงสุด

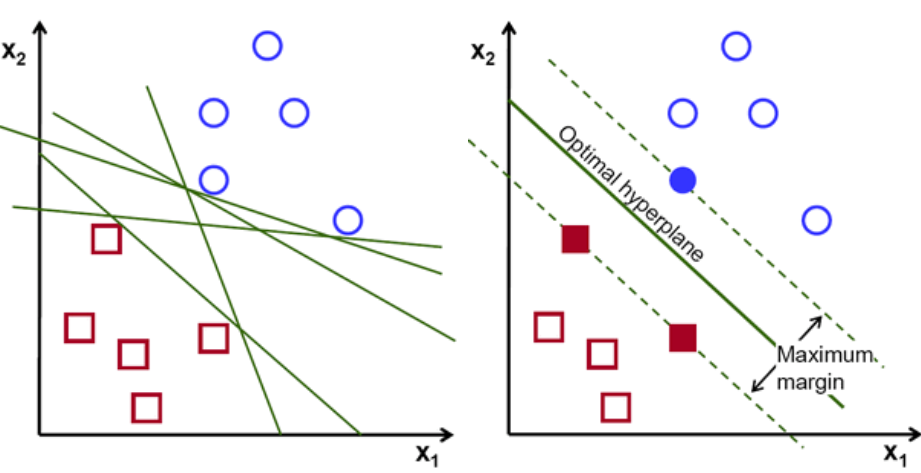
เครดิตภาพ

ยกตัวอย่างการแบ่งเซลล์ว่าดีและไม่ดี เซลล์ xᵢ ถูกกำหนดให้เป็น เวกเตอร์คุณลักษณะเหล่านี้แต่ละตัวมีป้ายกำกับคลาส yᵢ คลาส yᵢ สามารถเป็นได้ทั้ง +ve หรือ -ve (เช่น good=1, not good =-1) สมการของไฮเปอร์เพลนคือ y= wx + b = 0 โดยที่ W และ b เป็นพารามิเตอร์ของเส้น สมการก่อนหน้านี้ คืนค่า ≥ 1 สำหรับตัวอย่างสำหรับ +ve คลาส และ ≤-1 สำหรับ -ve ตัวอย่างคลาส

แต่มันหาไฮเปอร์เพลนนี้ได้อย่างไร? ไฮเปอร์เพลนถูกกำหนดโดยการหาค่าที่เหมาะสมที่สุด w หรือ น้ำหนัก และ b หรือ การสกัดกั้นซึ่ง และหาค่าที่เหมาะสมเหล่านี้ได้โดยการลดฟังก์ชันต้นทุนให้เหลือน้อยที่สุด เมื่ออัลกอริทึมรวบรวมค่าที่เหมาะสมที่สุดเหล่านี้ โมเดล SVM หรือฟังก์ชัน line f(x) จะจำแนกประเภททั้งสองอย่างมีประสิทธิภาพ

โดยสรุป ไฮเปอร์เพลนที่เหมาะสมที่สุดมีสมการ w.x+b = 0 เวกเตอร์แนวรับด้านซ้ายมีสมการ w.x+b=-1 และเวกเตอร์แนวรับด้านขวามี w.x+b=1

ดังนั้น ระยะห่าง d ระหว่างลิเอนคู่ขนานสองตัว Ay = Bx + c1 และ Ay = Bx + c2 ถูกกำหนดโดย d = |C1–C2|/√A^2 + B^2 ด้วยสูตรนี้ เรามีระยะห่างระหว่างเวกเตอร์สนับสนุนทั้งสองเป็น 2/||w||

ฟังก์ชันต้นทุนสำหรับ SVM ดูเหมือนสมการด้านล่าง:

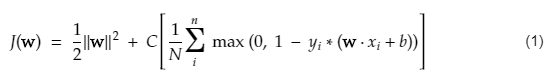
เครดิตภาพ

ฟังก์ชันการสูญเสีย SVM

ในสมการฟังก์ชันต้นทุนด้านบน พารามิเตอร์ λ แสดงว่า λ ที่ใหญ่กว่า ให้ส่วนต่างที่กว้างกว่า และ λ ที่เล็กกว่าจะให้ผลต่างที่น้อยกว่า นอกจากนี้ การคำนวณระดับความชันของฟังก์ชันต้นทุนจะคำนวณและน้ำหนักจะได้รับการอัปเดตในทิศทางที่ลดฟังก์ชันที่สูญหายลง

อ่าน: พีชคณิตเชิงเส้นสำหรับการเรียนรู้ของเครื่อง: แนวคิดที่สำคัญ เหตุใดจึงต้องเรียนรู้ก่อน ML

อัลกอริทึมสำหรับ SVM . แบบไม่เชิงเส้น

ในลักษณนาม SVM ตรงไปตรงมาที่จะมีไฮเปอร์ระนาบเชิงเส้นระหว่างสองคลาสนี้ แต่คำถามที่น่าสนใจก็คือ ถ้าข้อมูลไม่แยกเชิงเส้นควรทำอย่างไร? สำหรับสิ่งนี้ อัลกอริทึม SVM มีวิธีการที่เรียกว่าเคล็ดลับเคอร์เนล

ฟังก์ชันเคอร์เนล SVM ใช้พื้นที่อินพุตมิติต่ำและแปลงเป็นพื้นที่มิติที่สูงกว่า พูดง่ายๆ ก็คือ มันแปลงปัญหาที่แยกไม่ออกเป็นปัญหาที่แยกไม่ออก ดำเนินการแปลงข้อมูลที่ซับซ้อนตามป้ายกำกับหรือเอาต์พุตที่กำหนด

ดูแผนภาพด้านล่างเพื่อทำความเข้าใจการแปลงข้อมูลให้ดีขึ้น ชุดของจุดข้อมูลทางด้านซ้ายไม่สามารถแยกเป็นเส้นตรงได้อย่างชัดเจน แต่เมื่อเรานำฟังก์ชัน Φ ไปใช้กับชุดของจุดข้อมูล เราจะแปลงจุดข้อมูลในมิติที่สูงขึ้นซึ่งแยกออกได้โดยใช้ระนาบ

เครดิตภาพ

ในการแยกจุดข้อมูลที่ไม่สามารถแยกเชิงเส้นได้ เราต้องเพิ่มมิติพิเศษ สำหรับข้อมูลเชิงเส้น ใช้สองมิติ นั่นคือ x และ y สำหรับจุดข้อมูลเหล่านี้ เราเพิ่มมิติที่สาม เช่น z สำหรับตัวอย่างด้านล่าง ให้ z=x² +y²

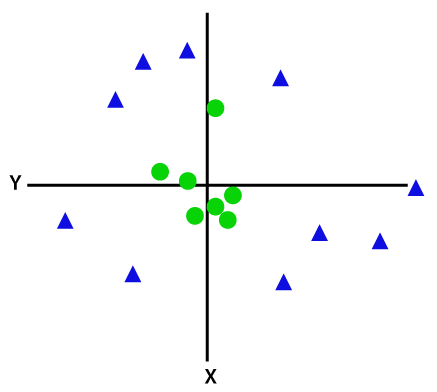
เครดิตภาพ

ฟังก์ชัน z นี้หรือมิติที่เพิ่มเข้ามาจะเปลี่ยนพื้นที่ตัวอย่างและภาพด้านบนจะเป็นดังนี้:

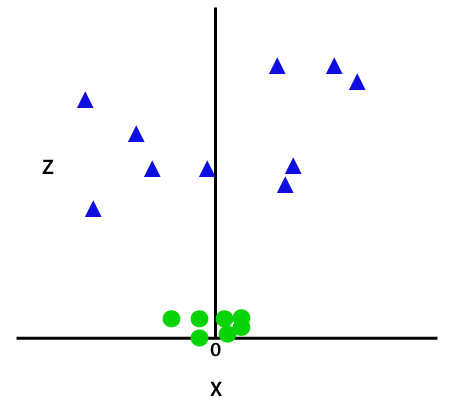
เครดิตภาพ

ในการวิเคราะห์อย่างใกล้ชิด เห็นได้ชัดว่าจุดข้อมูลข้างต้นสามารถแยกออกได้โดยใช้ฟังก์ชันเส้นตรงที่ขนานกับแกน x หรือเอียงเป็นมุม ฟังก์ชันเคอร์เนลประเภทต่างๆ มีอยู่ — ฟังก์ชันเชิงเส้น ไม่เชิงเส้น พหุนาม ฟังก์ชันพื้นฐานแนวรัศมี (RBF) และซิกมอยด์

สิ่งที่ RBF ทำในคำง่ายๆ คือ ถ้าเราเลือกจุดใดจุดหนึ่ง ผลลัพธ์ของ RBF จะเป็นบรรทัดฐานของระยะห่างระหว่างจุดนั้นกับจุดคงที่บางจุด กล่าวอีกนัยหนึ่ง เราสามารถออกแบบมิติ az ด้วยผลตอบแทนของ RBF นี้ ซึ่งโดยทั่วไปจะให้ 'ความสูง' ขึ้นอยู่กับว่าจุดนั้นอยู่ไกลจากจุดใดจุดหนึ่ง

เช็คเอาท์: 6 ประเภทของฟังก์ชันการเปิดใช้งานในโครงข่ายประสาทเทียมที่คุณต้องรู้

เคอร์เนลตัวไหนให้เลือก?

วิธีที่ดีในการพิจารณาว่าเคอร์เนลใดเหมาะสมที่สุดคือการสร้างแบบจำลองต่างๆ ที่มีเมล็ดที่แตกต่างกัน จากนั้นประมาณประสิทธิภาพแต่ละรายการ และเปรียบเทียบผลลัพธ์ในท้ายที่สุด จากนั้นคุณเลือกเคอร์เนลที่มีผลลัพธ์ที่ดีที่สุด ให้เฉพาะเจาะจงในการประมาณประสิทธิภาพของแบบจำลองในสิ่งที่แตกต่างจากการสังเกตโดยใช้ K-Fold Cross-Validation และพิจารณาตัวชี้วัดต่างๆ เช่น ความแม่นยำ, คะแนน F1 เป็นต้น

SVM ใน Python และ R

เมธอด fit ใน python ฝึกโมเดล SVM บนข้อมูล Xtrain และ ytrain ที่แยกจากกัน โดยเฉพาะอย่างยิ่ง วิธี fit จะรวบรวมข้อมูลใน Xtrain และ ytrain จากนั้นจะคำนวณเวกเตอร์สนับสนุนทั้งสอง

เมื่อประเมินเวกเตอร์สนับสนุนเหล่านี้แล้ว โมเดลตัวแยกประเภทจะได้รับการตั้งค่าอย่างสมบูรณ์เพื่อสร้างการคาดการณ์ใหม่ด้วยฟังก์ชันการทำนาย เนื่องจากต้องการเพียงเวกเตอร์สนับสนุนเพื่อแยกข้อมูลใหม่ ตอนนี้คุณอาจได้ผลลัพธ์ที่แตกต่างกันใน Python และ R ดังนั้นอย่าลืมตรวจสอบค่าของพารามิเตอร์ seed

บทสรุป

ในบทความนี้ เราได้พิจารณาอัลกอริธึม Support Vector Machine โดยละเอียด ขอบคุณที่สละเวลา. ติดตามบทความดังกล่าวเพิ่มเติม

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT- สถานะศิษย์เก่า B, 5+ โครงการหลักที่ใช้งานได้จริง & ความช่วยเหลือด้านงานกับบริษัทชั้นนำ

รุ่น Support Vector Machine เหมาะสำหรับปัญหาประเภทใดบ้าง

Support Vector Machines (SVM) ทำงานได้ดีที่สุดกับข้อมูลที่แยกเชิงเส้นได้ เช่น ข้อมูลที่สามารถแยกออกเป็นสองคลาสที่แตกต่างกันโดยใช้เส้นตรงหรือไฮเปอร์เพลน การใช้ SVM ที่พบบ่อยที่สุดอย่างหนึ่งคือการจดจำใบหน้า เทคนิค eigenfaces เป็นตัวอย่างหนึ่งของ SVM ซึ่งลดมิติของภาพใบหน้าและใช้สำหรับจดจำใบหน้า เทคนิคนี้มีพื้นฐานอยู่บนสมมติฐานที่ว่าใบหน้าสามารถคิดได้ว่าเป็นเวกเตอร์ในพื้นที่เวกเตอร์มิติสูงและมิติจะลดลงโดยการปรับไฮเปอร์สเฟียร์เข้ากับข้อมูล ทำให้เราสามารถจับคู่ใบหน้าสองหน้าที่มีขนาดต่างกันหรือหมุนได้ SVM ยังใช้ในการจำแนกประเภท

แอปพลิเคชันของ SVM ในชีวิตจริงมีอะไรบ้าง

สามารถใช้ SVM สำหรับข้อมูลต่อเนื่องได้หรือไม่

SVM ใช้เพื่อสร้างแบบจำลองการจัดหมวดหมู่ ดังนั้นถ้าคุณมีลักษณนาม มันต้องทำงานกับสองคลาสเท่านั้น หากคุณมีข้อมูลอย่างต่อเนื่อง คุณจะต้องเปลี่ยนข้อมูลนั้นเป็นคลาส กระบวนการนี้เรียกว่าการลดมิติ ตัวอย่างเช่น หากคุณมีบางอย่าง เช่น อายุ ส่วนสูง น้ำหนัก เกรด ฯลฯ คุณสามารถใช้ค่าเฉลี่ยของข้อมูลนั้นและทำให้มันใกล้ชิดกับชั้นเรียนใดกลุ่มหนึ่งมากขึ้น ซึ่งจะทำให้การจัดหมวดหมู่ง่ายขึ้น