Support Vector Machines: Arten von SVM [Algorithmus erklärt]

Einführung

Genau wie andere Algorithmen im maschinellen Lernen, die die Aufgabe der Klassifikation (Entscheidungsbäume, Random Forest, K-NN) und Regression übernehmen, unterstützt Vector Machine oder SVM einen solchen Algorithmus im gesamten Pool. Es handelt sich um einen überwachten (erfordert gekennzeichnete Datensätze) maschinellen Lernalgorithmus, der für Probleme im Zusammenhang mit Klassifizierung oder Regression verwendet wird.

Es wird jedoch häufig bei Klassifizierungsproblemen angewendet. Der SVM-Algorithmus beinhaltet das Plotten jedes Datenelements als Punkt. Das Plotten erfolgt in einem n-dimensionalen Raum, wobei n die Anzahl der Merkmale bestimmter Daten ist. Dann wird die Klassifizierung durchgeführt, indem die am besten geeignete Hyperebene gefunden wird, die die zwei (oder mehr) Klassen effektiv trennt.

Die Begriffsunterstützungsvektoren sind nur Koordinaten eines einzelnen Merkmals. Warum Datenpunkte als Vektoren verallgemeinern, fragen Sie sich vielleicht. Bei realen Problemen gibt es Datensätze höherer Dimensionen. In höheren Dimensionen (n-Dimension) ist es sinnvoller, Vektorarithmetik und Matrizenmanipulationen durchzuführen, anstatt sie als Punkte zu betrachten.

Arten von SVM

Lineare SVM: Lineare SVM wird für Daten verwendet, die linear trennbar sind, dh für einen Datensatz, der durch Verwendung einer einzigen geraden Linie in zwei Kategorien eingeteilt werden kann. Solche Datenpunkte werden als linear trennbare Daten bezeichnet, und der Klassifikator wird als linearer SVM-Klassifikator beschrieben verwendet.

Nichtlineare SVM: Nichtlineare SVM wird für Daten verwendet, die nichtlinear trennbare Daten sind, dh eine gerade Linie kann nicht verwendet werden, um den Datensatz zu klassifizieren. Dazu verwenden wir einen sogenannten Kernel-Trick, der Datenpunkte in eine höhere Dimension setzt, wo sie mit Ebenen oder anderen mathematischen Funktionen getrennt werden können. Solche Datenpunkte werden als nichtlineare Daten bezeichnet, und der verwendete Klassifikator wird als nichtlinearer SVM-Klassifikator bezeichnet.

Algorithmus für lineare SVM

Lassen Sie uns über ein binäres Klassifizierungsproblem sprechen. Die Aufgabe besteht darin, einen Testpunkt so genau wie möglich effizient in eine der Klassen einzuordnen. Im Folgenden sind die Schritte des SVM-Prozesses aufgeführt.

Zunächst werden die zu den beiden Klassen gehörenden Punktesätze geplottet und wie unten gezeigt visualisiert. In einem 2-D-Raum können wir diese beiden Klassen effizient trennen, indem wir einfach eine gerade Linie anwenden. Aber es kann viele Linien geben, die diese Klassen klassifizieren können. Es gibt eine Reihe von Linien oder Hyperebenen (grüne Linien) zur Auswahl. Die offensichtliche Frage wird sein, welche Linie von all diesen Linien für die Klassifizierung geeignet ist?

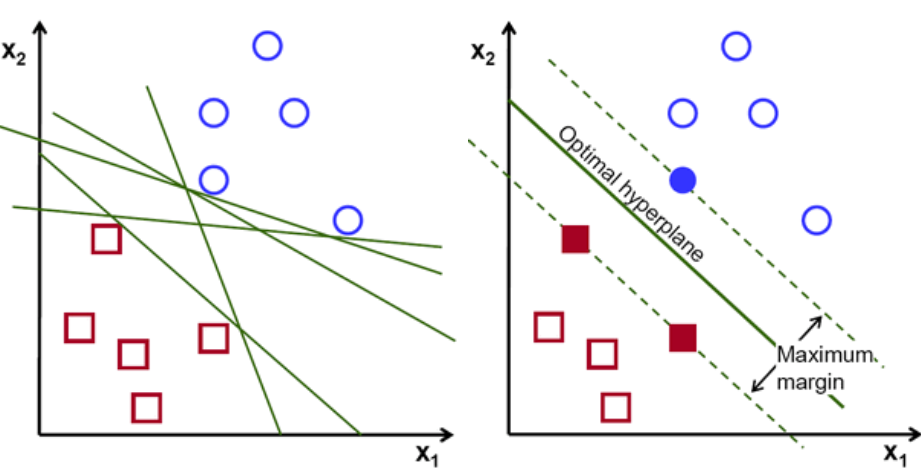
Satz von Hyperebenen, Bildnachweis

Wählen Sie grundsätzlich die Hyperebene aus, die die beiden Klassen besser trennt. Wir tun dies, indem wir den Abstand zwischen dem nächsten Datenpunkt und der Hyperebene maximieren. Je größer der Abstand, desto besser ist die Hyperebene und es ergeben sich bessere Klassifikationsergebnisse. In der Abbildung unten ist zu sehen, dass die ausgewählte Hyperebene den maximalen Abstand vom nächstgelegenen Punkt jeder dieser Klassen hat.

Zur Erinnerung: Die beiden gepunkteten Linien, die parallel zur Hyperebene verlaufen und die nächstgelegenen Punkte jeder der Klassen kreuzen, werden als Stützvektoren der Hyperebene bezeichnet. Nun wird der Trennungsabstand zwischen den Stützvektoren und der Hyperebene als Rand bezeichnet. Und der Zweck des SVM-Algorithmus besteht darin, diesen Spielraum zu maximieren. Die optimale Hyperebene ist die Hyperebene mit maximalem Spielraum.

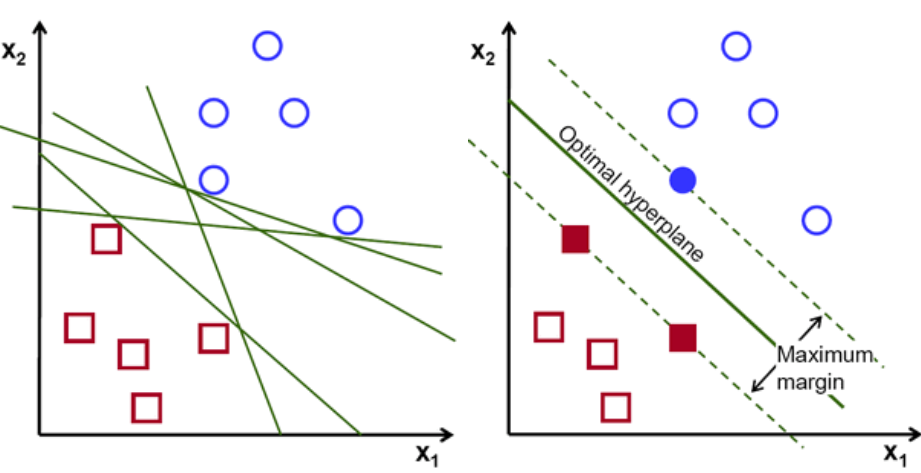
Bildnachweis

Nehmen Sie zum Beispiel die Klassifizierung von Zellen in gut und schlecht. die Zelle xᵢ ist als ein Jeder dieser Merkmalsvektoren ist mit einer Klasse yᵢ gekennzeichnet. Die Klasse yᵢ kann entweder ein +ve oder -ve sein (zB gut=1, nicht gut =-1). Die Gleichung der Hyperebene lautet y= wx + b = 0. Wobei W und b Linienparameter sind. Die frühere Gleichung gibt einen Wert ≥ 1 für Beispiele für die +ve-Klasse und ≤-1 für Beispiele für die -ve-Klasse zurück.

Aber wie findet es diese Hyperebene? Die Hyperebene wird definiert, indem die optimalen Werte w oder Gewichte und b oder Achsenabschnitt gefunden werden. Und diese optimalen Werte werden durch Minimieren der Kostenfunktion gefunden. Sobald der Algorithmus diese optimalen Werte erfasst, klassifiziert das SVM-Modell oder die Linienfunktion f(x) die beiden Klassen effizient.

Kurz gesagt, die optimale Hyperebene hat die Gleichung w.x+b = 0. Der linke Unterstützungsvektor hat die Gleichung w.x+b=-1 und der rechte Unterstützungsvektor hat w.x+b=1.

Somit ist der Abstand d zwischen zwei parallelen Linien Ay = Bx + c1 und Ay = Bx + c2 gegeben durch d = |C1–C2|/√A^2 + B^2. Mit dieser Formel haben wir den Abstand zwischen den beiden Stützvektoren als 2/||w||.

Die Kostenfunktion für SVM sieht wie die folgende Gleichung aus:

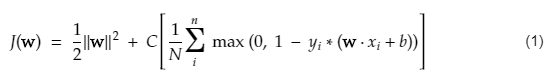
Bildnachweis

SVM-Verlustfunktion

In der obigen Kostenfunktionsgleichung bedeutet der λ-Parameter, dass ein größeres λ einen breiteren Spielraum bietet und ein kleineres λ einen kleineren Spielraum ergeben würde. Außerdem wird der Gradient der Kostenfunktion berechnet und die Gewichte werden in der Richtung aktualisiert, die die Verlustfunktion verringert.

Lesen Sie: Lineare Algebra für maschinelles Lernen: Kritische Konzepte, warum Lernen vor ML

Algorithmus für nichtlineare SVM

Im SVM-Klassifikator ist es einfach, eine lineare Hyperebene zwischen diesen beiden Klassen zu haben. Es stellt sich jedoch eine interessante Frage: Was ist zu tun, wenn die Daten nicht linear trennbar sind? Dafür hat der SVM-Algorithmus eine Methode namens Kernel-Trick.

Die SVM-Kernelfunktion nimmt einen niederdimensionalen Eingaberaum auf und wandelt ihn in einen höherdimensionalen Raum um. In einfachen Worten, es wandelt das nicht trennbare Problem in ein trennbares Problem um. Es führt komplexe Datentransformationen basierend auf den Labels oder Ausgaben durch, die sie definieren

Sehen Sie sich das Diagramm unten an, um die Datenumwandlung besser zu verstehen. Der Satz von Datenpunkten auf der linken Seite ist eindeutig nicht linear trennbar. Aber wenn wir eine Funktion Φ auf die Menge von Datenpunkten anwenden, erhalten wir transformierte Datenpunkte in einer höheren Dimension, die über eine Ebene trennbar ist.

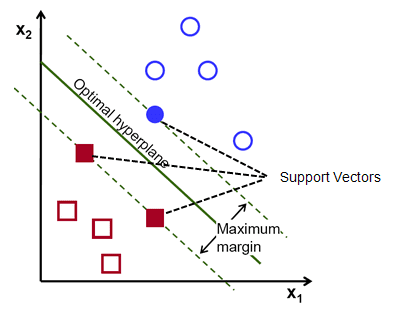
Bildnachweis

Um nicht linear trennbare Datenpunkte zu trennen, müssen wir eine zusätzliche Dimension hinzufügen. Für lineare Daten wurden zwei Dimensionen verwendet, d. h. x und y. Für diese Datenpunkte fügen wir eine dritte Dimension hinzu, sagen wir z. Für das folgende Beispiel sei z=x² +y².

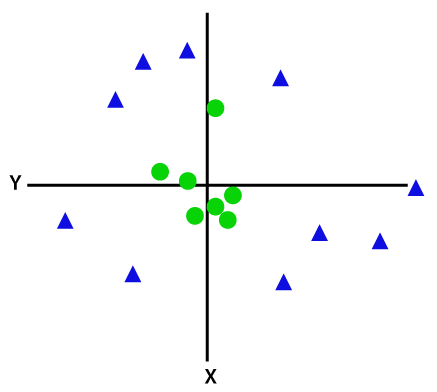
Bildnachweis

Diese z-Funktion oder die hinzugefügte Dimensionalität transformiert den Probenraum und das obige Bild wird wie folgt:

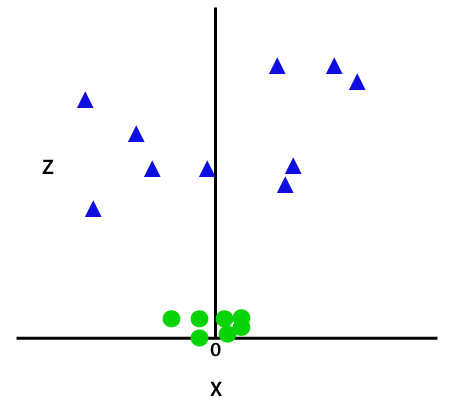
Bildnachweis

Bei näherer Analyse wird deutlich, dass die obigen Datenpunkte durch eine Geradenfunktion getrennt werden können, die entweder parallel zur x-Achse oder in einem Winkel geneigt ist. Es gibt verschiedene Arten von Kernelfunktionen – lineare, nichtlineare, polynomiale, radiale Basisfunktionen (RBF) und Sigmoidfunktionen.

Was RBF in einfachen Worten macht, ist: Wenn wir einen Punkt auswählen, ist das Ergebnis eines RBF die Norm der Entfernung zwischen diesem Punkt und einem festen Punkt. Mit anderen Worten, wir können eine z-Dimension mit den Erträgen dieses RBF entwerfen, was normalerweise „Höhe“ ergibt, je nachdem, wie weit der Punkt von einem bestimmten Punkt entfernt ist.

Check out: 6 Arten von Aktivierungsfunktionen in neuronalen Netzwerken, die Sie kennen müssen

Welchen Kernel wählen?

Eine gute Methode, um festzustellen, welcher Kernel am besten geeignet ist, besteht darin, verschiedene Modelle mit unterschiedlichen Kerneln zu erstellen, dann ihre Leistung zu schätzen und schließlich die Ergebnisse zu vergleichen. Dann wählen Sie den Kernel mit den besten Ergebnissen aus. Achten Sie besonders darauf, die Leistung des Modells bei ungleichen Beobachtungen zu schätzen, indem Sie die K-Fold-Kreuzvalidierung verwenden, und berücksichtigen Sie verschiedene Metriken wie Genauigkeit, F1-Ergebnis usw.

SVM in Python und R

Die Fit-Methode in Python trainiert einfach das SVM-Modell auf Xtrain- und Ytrain-Daten, die getrennt wurden. Genauer gesagt setzt die Fit-Methode die Daten in Xtrain und ytrain zusammen und berechnet daraus die beiden Unterstützungsvektoren.

Sobald diese Unterstützungsvektoren geschätzt sind, ist das Klassifikatormodell vollständig darauf eingestellt, neue Vorhersagen mit der Vorhersagefunktion zu erzeugen, da es nur die Unterstützungsvektoren benötigt, um die neuen Daten zu trennen. Jetzt erhalten Sie möglicherweise unterschiedliche Ergebnisse in Python und in R, überprüfen Sie also unbedingt den Wert des Seed-Parameters.

Fazit

In diesem Artikel haben wir uns den Support Vector Machine-Algorithmus im Detail angesehen. Vielen Dank für Ihre Zeit. Schalten Sie ein für mehr solcher Artikel.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.

Für welche Probleme eignen sich Support Vector Machine-Modelle?

Support Vector Machines (SVM) arbeiten am besten mit linear trennbaren Daten, dh Daten, die unter Verwendung einer geraden Linie oder einer Hyperebene in zwei unterschiedliche Klassen getrennt werden können. Eine der häufigsten Anwendungen von SVM ist die Gesichtserkennung. Die Eigenfaces-Technik ist ein Beispiel für SVM, das eine Dimensionsreduktion von Gesichtsbildern durchführt und zur Gesichtserkennung verwendet wird. Diese Technik basiert auf der Prämisse, dass Gesichter als Vektoren in einem hochdimensionalen Vektorraum betrachtet werden können und die Dimensionalität reduziert wird, indem eine Hypersphäre an die Daten angepasst wird. Dies ermöglicht es uns, zwei Gesichter abzugleichen, die eine unterschiedliche Größe haben oder gedreht sind. SVM wird auch in der Klassifizierung verwendet.

Was sind die Anwendungen von SVMs im wirklichen Leben?

Kann SVM für kontinuierliche Daten verwendet werden?

SVM wird verwendet, um ein Klassifizierungsmodell zu erstellen. Wenn Sie also einen Klassifikator haben, muss dieser mit nur zwei Klassen arbeiten. Wenn Sie kontinuierliche Daten haben, müssen Sie diese Daten in Klassen umwandeln, der Prozess wird als Dimensionsreduktion bezeichnet. Wenn Sie beispielsweise etwas wie Alter, Größe, Gewicht, Klasse usw. haben, können Sie den Mittelwert dieser Daten nehmen und ihn entweder näher an die eine oder andere Klasse heranführen, was dann die Klassifizierung erleichtert.