Mendukung Mesin Vektor: Jenis SVM [Algoritma Dijelaskan]

pengantar

Sama seperti algoritma lain dalam pembelajaran mesin yang melakukan tugas klasifikasi (pohon keputusan, hutan acak, K-NN) dan regresi, Support Vector Machine atau SVM salah satu algoritma tersebut di seluruh kumpulan. Ini adalah algoritma pembelajaran mesin yang diawasi (memerlukan kumpulan data berlabel) yang digunakan untuk masalah yang berkaitan dengan klasifikasi atau regresi.

Namun, ini sering diterapkan dalam masalah klasifikasi. Algoritma SVM memerlukan plotting setiap item data sebagai titik. Plotting dilakukan dalam ruang n-dimensi di mana n adalah jumlah fitur dari data tertentu. Kemudian, klasifikasi dilakukan dengan mencari hyperplane yang paling cocok yang memisahkan dua (atau lebih) kelas secara efektif.

Istilah vektor pendukung hanyalah koordinat dari fitur individual. Mengapa menggeneralisasi titik data sebagai vektor, Anda mungkin bertanya. Dalam masalah dunia nyata, terdapat kumpulan data dengan dimensi yang lebih tinggi. Dalam dimensi yang lebih tinggi (dimensi-n), lebih masuk akal untuk melakukan aritmatika vektor dan manipulasi matriks daripada menganggapnya sebagai titik.

Jenis SVM

Linear SVM : Linear SVM digunakan untuk data yang dapat dipisahkan secara linier yaitu untuk dataset yang dapat dikategorikan menjadi dua kategori dengan memanfaatkan satu garis lurus. Titik data tersebut disebut sebagai data yang dapat dipisahkan secara linier, dan pengklasifikasi yang digunakan digambarkan sebagai pengklasifikasi SVM Linear.

SVM Non-linear: SVM Non-Linear digunakan untuk data yang merupakan data yang tidak dapat dipisahkan secara linier yaitu garis lurus tidak dapat digunakan untuk mengklasifikasikan kumpulan data. Untuk ini, kami menggunakan sesuatu yang dikenal sebagai trik kernel yang menetapkan titik data dalam dimensi yang lebih tinggi di mana mereka dapat dipisahkan menggunakan bidang atau fungsi matematika lainnya. Titik data tersebut disebut sebagai data non-linear, dan pengklasifikasi yang digunakan disebut sebagai pengklasifikasi SVM Non-linear.

Algoritma untuk SVM Linier

Mari kita bicara tentang masalah klasifikasi biner. Tugasnya adalah untuk secara efisien mengklasifikasikan titik tes di salah satu kelas seakurat mungkin. Berikut ini adalah langkah-langkah yang terlibat dalam proses SVM.

Pertama, set poin milik dua kelas diplot dan divisualisasikan seperti yang ditunjukkan di bawah ini. Dalam ruang 2 dimensi hanya dengan menerapkan garis lurus, kita dapat membagi dua kelas ini secara efisien. Tetapi ada banyak baris yang dapat mengklasifikasikan kelas-kelas ini. Ada satu set garis atau hyperplanes (garis hijau) untuk dipilih. Pertanyaan yang jelas adalah, dari semua garis ini, garis mana yang cocok untuk klasifikasi?

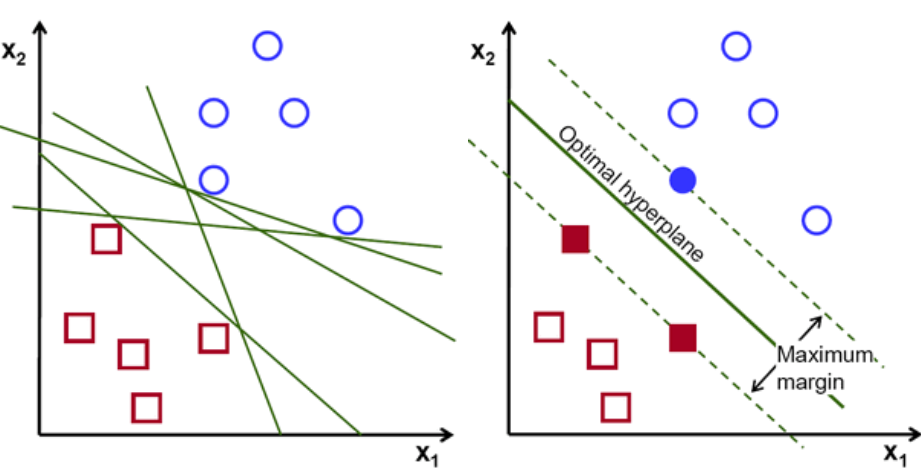
set hyper-pesawat, Kredit gambar

Pada dasarnya, Pilih hyper-plane yang memisahkan dua kelas dengan lebih baik. Kami melakukan ini dengan memaksimalkan jarak antara titik data terdekat dan hyper-plane. Semakin besar jarak, semakin baik hyperplane dan hasil klasifikasi yang lebih baik terjadi. Dapat dilihat pada gambar di bawah ini bahwa hyperplane yang dipilih memiliki jarak maksimum dari titik terdekat dari masing-masing kelas tersebut.

Sebagai pengingat, dua garis putus-putus yang sejajar dengan hyperplane yang melintasi titik terdekat dari masing-masing kelas disebut sebagai support vector dari hyperplane. Sekarang, jarak pemisahan antara vektor pendukung dan hyperplane disebut margin. Dan tujuan dari algoritma SVM adalah untuk memaksimalkan margin ini. Hyperplane yang optimal adalah hyperplane dengan margin maksimum.

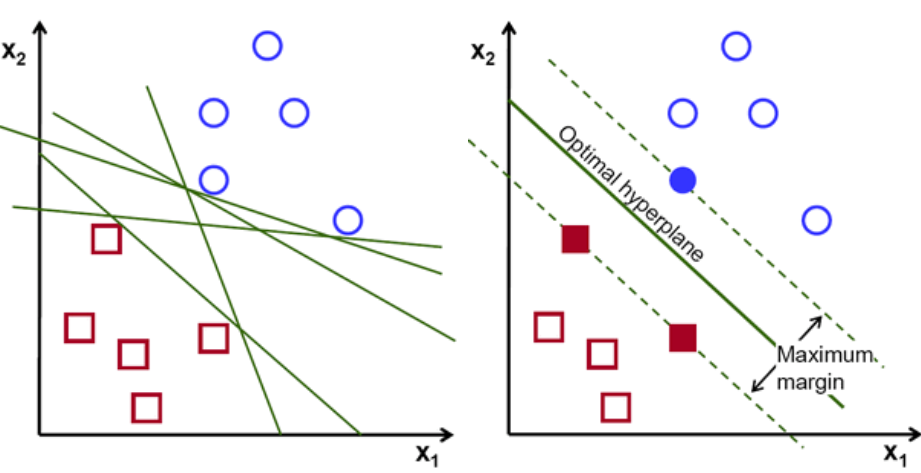
Kredit gambar

Ambil contoh mengklasifikasikan sel sebagai baik dan buruk. sel xᵢ didefinisikan sebagai Masing-masing vektor fitur ini diberi label dengan kelas yᵢ. Kelas yᵢ dapat berupa +ve atau -ve (mis. good=1, not good =-1). Persamaan hyperplane adalah y= wx + b = 0. Dimana W dan b adalah parameter garis. Persamaan sebelumnya mengembalikan nilai 1 untuk contoh kelas +ve dan -1 untuk contoh kelas -ve.

Tapi, Bagaimana cara menemukan hyperplane ini? Hyperplane didefinisikan dengan mencari nilai optimal w atau bobot dan b atau intersep yang. Dan nilai-nilai optimal ini ditemukan dengan meminimalkan fungsi biaya. Setelah algoritme mengumpulkan nilai-nilai optimal ini, model SVM atau fungsi garis f(x) secara efisien mengklasifikasikan dua kelas.

Singkatnya, hyperplane optimal memiliki persamaan w.x+b = 0. Vektor pendukung kiri memiliki persamaan w.x+b=-1 dan vektor pendukung kanan memiliki w.x+b=1.

Jadi jarak d antara dua gadai sejajar Ay = Bx + c1 dan Ay = Bx + c2 diberikan oleh d = |C1–C2|/√A^2 + B^2. Dengan rumus ini, kita memiliki jarak antara dua vektor pendukung sebagai 2/||w||.

Fungsi biaya untuk SVM terlihat seperti persamaan di bawah ini:

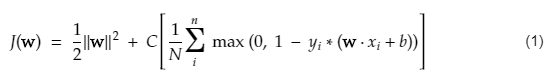
Kredit gambar

Fungsi kehilangan SVM

Dalam persamaan fungsi biaya di atas, parameter menunjukkan bahwa yang lebih besar memberikan margin yang lebih luas, dan yang lebih kecil akan menghasilkan margin yang lebih kecil. Selanjutnya, gradien fungsi biaya dihitung dan bobot diperbarui ke arah yang menurunkan fungsi yang hilang.

Baca: Aljabar Linier untuk Machine Learning: Konsep Kritis, Mengapa Belajar Sebelum ML

Algoritma untuk SVM Non-linear

Dalam pengklasifikasi SVM, sangat mudah untuk memiliki bidang hiper linier di antara kedua kelas ini. Namun, pertanyaan menarik yang muncul adalah, bagaimana jika data tidak dapat dipisahkan secara linier, apa yang harus dilakukan? Untuk ini, algoritma SVM memiliki metode yang disebut trik kernel.

Fungsi kernel SVM mengambil ruang input berdimensi rendah dan mengubahnya menjadi ruang berdimensi lebih tinggi. Dengan kata sederhana, ini mengubah masalah yang tidak dapat dipisahkan menjadi masalah yang dapat dipisahkan. Ia melakukan transformasi data yang kompleks berdasarkan label atau output yang mendefinisikannya

Perhatikan diagram di bawah ini untuk lebih memahami transformasi data. Kumpulan titik data di sebelah kiri jelas tidak dapat dipisahkan secara linier. Tetapi ketika kita menerapkan fungsi ke himpunan titik data, kita mendapatkan titik data yang diubah dalam dimensi yang lebih tinggi yang dapat dipisahkan melalui bidang.

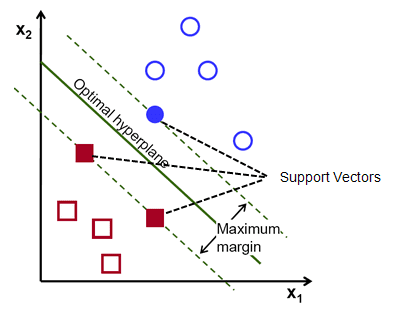
Kredit gambar

Untuk memisahkan titik data yang tidak dapat dipisahkan secara linier, kita harus menambahkan dimensi tambahan. Untuk data linier digunakan dua dimensi yaitu x dan y. Untuk titik data ini, kami menambahkan dimensi ketiga, katakanlah z. Untuk contoh di bawah ini biarkan z=x² +y².

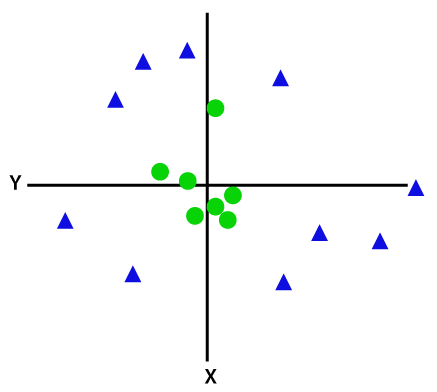
Kredit gambar

Fungsi z ini atau dimensi tambahan mengubah ruang sampel dan gambar di atas menjadi sebagai berikut:

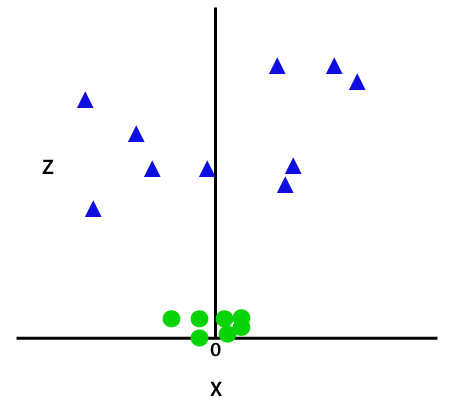
Kredit gambar

Pada analisis dekat, terbukti bahwa titik-titik data di atas dapat dipisahkan menggunakan fungsi garis lurus yang sejajar dengan sumbu x atau miring. Berbagai jenis fungsi kernel hadir — linear, nonlinier, polinomial, radial basis function (RBF), dan sigmoid.

Apa yang dilakukan RBF dengan kata sederhana adalah — jika kita memilih beberapa titik, hasil dari RBF akan menjadi norma jarak antara titik itu dan beberapa titik tetap. Dengan kata lain, kita dapat mendesain dimensi az dengan hasil RBF ini, yang biasanya memberikan 'tinggi' tergantung pada seberapa jauh titik tersebut dari beberapa titik.

Simak: 6 Jenis Fungsi Aktivasi di Jaringan Syaraf Tiruan yang Perlu Anda Ketahui

Kernel mana yang harus dipilih?

Metode yang bagus untuk menentukan kernel mana yang paling cocok adalah dengan membuat berbagai model dengan kernel yang berbeda-beda, kemudian memperkirakan kinerjanya masing-masing, dan akhirnya membandingkan hasilnya. Kemudian Anda memilih kernel dengan hasil terbaik. Khusus untuk memperkirakan kinerja model pada pengamatan yang berbeda dengan menggunakan K-Fold Cross-Validation dan pertimbangkan metrik yang berbeda seperti Akurasi, Skor F1, dll.

SVM dengan Python dan R

Metode fit pada python cukup melatih model SVM pada data Xtrain dan ytrain yang telah dipisahkan. Lebih khusus lagi, metode fit akan mengumpulkan data dalam Xtrain dan ytrain, dan dari situ akan menghitung dua support vector.

Setelah vektor pendukung ini diperkirakan, model pengklasifikasi sepenuhnya diatur untuk menghasilkan prediksi baru dengan fungsi prediksi karena hanya membutuhkan vektor pendukung untuk memisahkan data baru. Sekarang Anda mungkin mendapatkan hasil yang berbeda dalam Python dan R, jadi pastikan untuk memeriksa nilai parameter seed.

Kesimpulan

Pada artikel ini, kita melihat algoritma Support Vector Machine secara mendetail. Terima kasih atas waktunya. Tune in untuk lebih banyak artikel seperti itu.

Jika Anda tertarik untuk mempelajari lebih lanjut tentang pembelajaran mesin, lihat PG Diploma IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk para profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ studi kasus & tugas, IIIT- B Status alumni, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.

Jenis masalah apa yang cocok untuk model Support Vector Machine?

Support Vector Machines (SVM) bekerja paling baik pada data yang dapat dipisahkan secara linier, yaitu data yang dapat dipisahkan menjadi dua kelas yang berbeda menggunakan garis lurus atau hyperplane. Salah satu kegunaan SVM yang paling umum adalah dalam pengenalan wajah. Teknik eigenfaces adalah salah satu contoh dari SVM, yang melakukan pengurangan dimensi citra wajah dan digunakan untuk pengenalan wajah. Teknik ini didasarkan pada premis bahwa wajah dapat dianggap sebagai vektor dalam ruang vektor berdimensi tinggi dan dimensinya dikurangi dengan menyesuaikan hypersphere ke data. Ini memungkinkan kita untuk mencocokkan dua wajah yang ukurannya berbeda, atau diputar. SVM juga digunakan dalam klasifikasi.

Apa aplikasi SVM dalam kehidupan nyata?

Bisakah SVM digunakan untuk data berkelanjutan?

SVM digunakan untuk membuat model klasifikasi. Jadi, jika Anda memiliki pengklasifikasi, itu harus bekerja dengan hanya dua kelas. Jika Anda memiliki data kontinu, maka Anda harus mengubah data itu menjadi kelas, prosesnya disebut pengurangan dimensi. Misalnya, jika Anda memiliki sesuatu seperti usia, tinggi, berat, nilai, dll., maka Anda dapat mengambil rata-rata dari data tersebut dan membuatnya lebih dekat ke salah satu kelas atau lainnya, yang kemudian akan membuat klasifikasi menjadi lebih mudah.