Машины опорных векторов: типы SVM [объяснение алгоритма]

Введение

Как и другие алгоритмы в машинном обучении, которые выполняют задачу классификации (деревья решений, случайный лес, K-NN) и регрессии, машина опорных векторов или SVM — один такой алгоритм во всем пуле. Это контролируемый (требует помеченных наборов данных) алгоритм машинного обучения, который используется для решения задач, связанных либо с классификацией, либо с регрессией.

Однако он часто применяется в задачах классификации. Алгоритм SVM влечет за собой построение каждого элемента данных в виде точки. Построение выполняется в n-мерном пространстве, где n — количество признаков конкретных данных. Затем выполняется классификация путем нахождения наиболее подходящей гиперплоскости, которая эффективно разделяет два (или более) класса.

Термин опорные векторы — это просто координаты отдельного объекта. Вы можете спросить, зачем обобщать точки данных как векторы. В реальных задачах существуют наборы данных более высоких измерений. В более высоких измерениях (n-измерение) имеет смысл выполнять векторные арифметические и матричные манипуляции, а не рассматривать их как точки.

Типы SVM

Линейный SVM: Линейный SVM используется для линейно разделимых данных, т. е. для набора данных, который можно разделить на две категории с помощью одной прямой линии. Такие точки данных называются линейно разделимыми данными, и используется классификатор, описанный как линейный классификатор SVM.

Нелинейный SVM: Нелинейный SVM используется для данных, которые являются нелинейно разделимыми данными, т.е. прямая линия не может использоваться для классификации набора данных. Для этого мы используем нечто, известное как трюк с ядром, который устанавливает точки данных в более высоком измерении, где их можно разделить с помощью плоскостей или других математических функций. Такие точки данных называются нелинейными данными, а используемый классификатор называется нелинейным классификатором SVM.

Алгоритм линейного SVM

Давайте поговорим о проблеме бинарной классификации. Задача состоит в том, чтобы максимально точно классифицировать контрольную точку в любом из классов. Ниже приведены шаги, связанные с процессом SVM.

Во-первых, набор точек, принадлежащих двум классам, отображается и визуализируется, как показано ниже. В двумерном пространстве, просто проведя прямую линию, мы можем эффективно разделить эти два класса. Но может быть много линий, которые могут классифицировать эти классы. Есть набор линий или гиперплоскостей (зеленые линии) на выбор. Возникнет очевидный вопрос: какая линия из всех этих линий подходит для классификации?

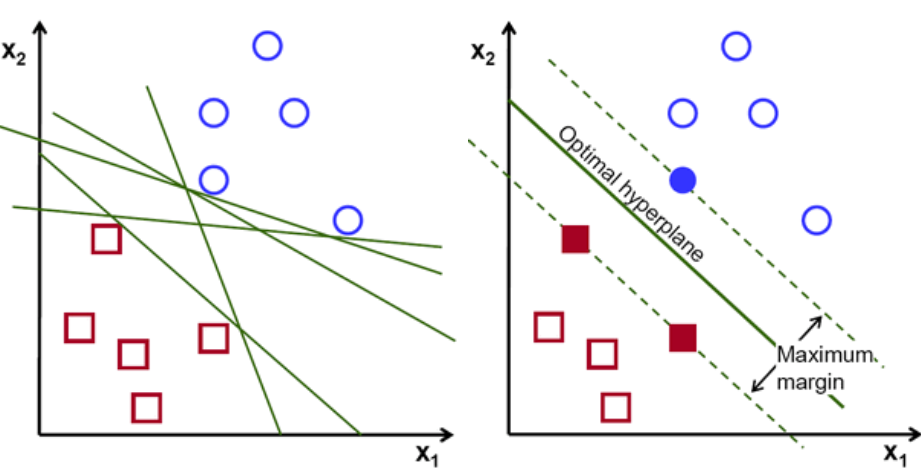
набор гиперсамолетов, изображение предоставлено

По сути, выберите гиперплоскость, которая лучше разделяет два класса. Мы делаем это, максимизируя расстояние между ближайшей точкой данных и гиперплоскостью. Чем больше расстояние, тем лучше гиперплоскость и лучше результаты классификации. На рисунке ниже видно, что выбранная гиперплоскость имеет максимальное расстояние от ближайшей точки каждого из этих классов.

Напомним, что две пунктирные линии, идущие параллельно гиперплоскости и пересекающие ближайшие точки каждого из классов, называются опорными векторами гиперплоскости. Теперь расстояние между опорными векторами и гиперплоскостью называется запасом. И цель алгоритма SVM — максимизировать эту маржу. Оптимальная гиперплоскость — это гиперплоскость с максимальным запасом.

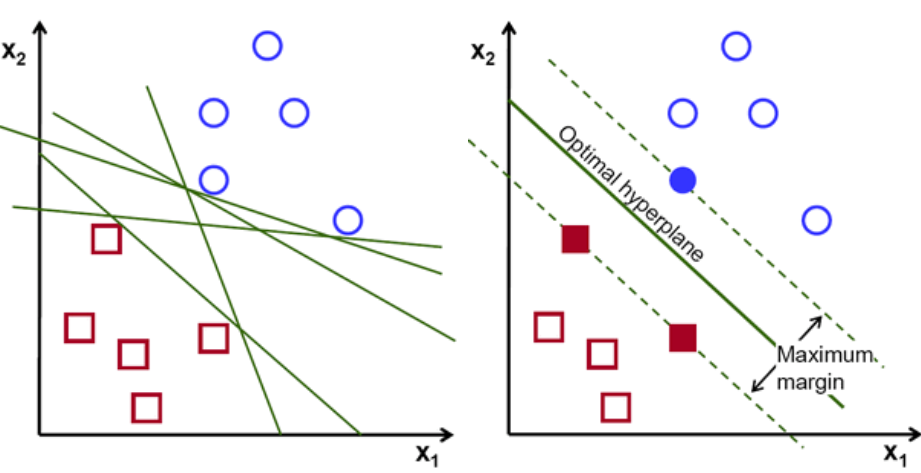
Кредит изображения

Возьмем, к примеру, классификацию клеток как хороших и плохих. ячейка xᵢ определяется как Каждый из этих векторов признаков помечен классом yᵢ. Класс yᵢ может быть либо +ve, либо -ve (например, хорошо = 1, не хорошо = -1). Уравнение гиперплоскости: y= wx + b = 0. Где W и b — параметры линии. Предыдущее уравнение возвращает значение ≥ 1 для примеров для класса +ve и ≤-1 для примеров класса -ve.

Но как он находит эту гиперплоскость? Гиперплоскость определяется путем нахождения оптимальных значений w или весов и b или пересечения которых. И эти оптимальные значения находятся путем минимизации функции стоимости. Как только алгоритм соберет эти оптимальные значения, модель SVM или линейная функция f(x) эффективно классифицирует два класса.

В двух словах, оптимальная гиперплоскость имеет уравнение w.x+b = 0. Левый опорный вектор имеет уравнение w.x+b=-1, а правый опорный вектор имеет w.x+b=1.

Таким образом, расстояние d между двумя параллельными связями Ay = Bx + c1 и Ay = Bx + c2 определяется как d = |C1–C2|/√A^2 + B^2. Используя эту формулу, мы получаем расстояние между двумя опорными векторами как 2/||w||.

Функция стоимости для SVM выглядит следующим образом:

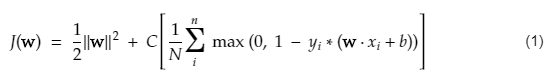
Кредит изображения

Функция потерь SVM

В приведенном выше уравнении функции стоимости параметр λ означает, что большее λ обеспечивает более широкую маржу, а меньшее λ дает меньшую маржу. Кроме того, вычисляется градиент функции стоимости, и веса обновляются в направлении, уменьшающем потерянную функцию.

Читайте: Линейная алгебра для машинного обучения: важные концепции, зачем учиться до машинного обучения

Алгоритм для нелинейного SVM

В классификаторе SVM прямолинейная гиперплоскость между этими двумя классами. Но возникает интересный вопрос: что делать, если данные не линейно разделимы? Для этого в алгоритме SVM есть метод, называемый трюком ядра.

Функция ядра SVM принимает низкоразмерное входное пространство и преобразует его в многомерное пространство. Проще говоря, он преобразует неразделимую проблему в разделимую. Он выполняет сложные преобразования данных на основе меток или выходных данных, которые их определяют.

Посмотрите на диаграмму ниже, чтобы лучше понять преобразование данных. Набор точек данных слева явно не является линейно разделимым. Но когда мы применяем функцию Φ к набору точек данных, мы получаем преобразованные точки данных в более высоком измерении, которое отделимо через плоскость.

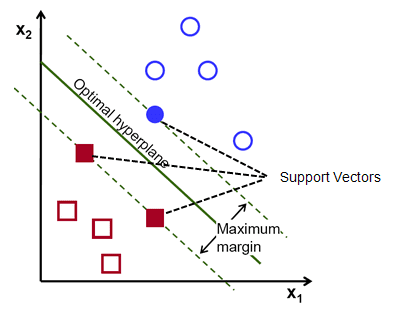
Кредит изображения

Чтобы разделить нелинейно разделимые точки данных, мы должны добавить дополнительное измерение. Для линейных данных использовались два измерения, то есть x и y. Для этих точек данных мы добавляем третье измерение, скажем, z. Для приведенного ниже примера пусть z=x² +y².

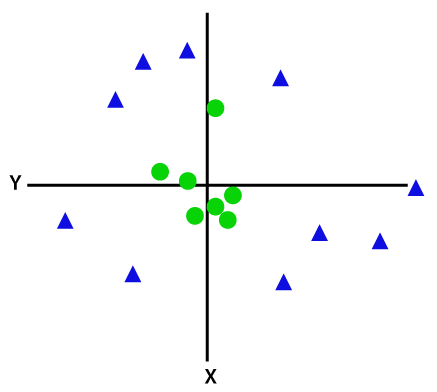
Кредит изображения

Эта функция z или добавленная размерность преобразует пространство выборки, и приведенное выше изображение станет следующим:

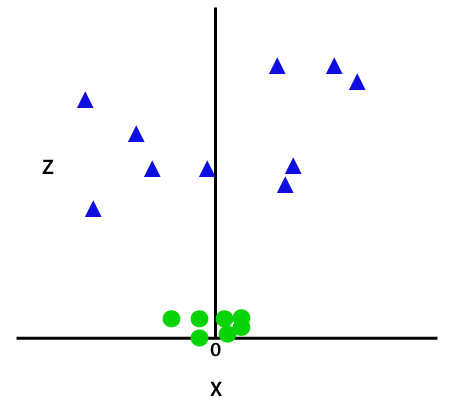
Кредит изображения

При внимательном анализе становится очевидным, что указанные выше точки данных можно разделить с помощью функции прямой линии, которая либо параллельна оси x, либо наклонена под углом. Присутствуют различные типы функций ядра — линейные, нелинейные, полиномиальные, радиальные базисные функции (РБФ) и сигмоидальные.

Простыми словами, RBF делает следующее: если мы выберем какую-то точку, результатом RBF будет норма расстояния между этой точкой и некоторой фиксированной точкой. Другими словами, мы можем спроектировать измерение az с выходами этого RBF, который обычно дает «высоту» в зависимости от того, насколько далеко точка находится от некоторой точки.

Проверьте: 6 типов функций активации в нейронных сетях, которые вам нужно знать

Какое ядро ​​выбрать?

Хороший способ определить, какое ядро ​​является наиболее подходящим, состоит в том, чтобы создать различные модели с различными ядрами, затем оценить производительность каждой из них и в конечном итоге сравнить результаты. Затем вы выбираете ядро ​​с лучшими результатами. Будьте особенно внимательны, чтобы оценить производительность модели на разных наблюдениях с помощью перекрестной проверки K-Fold и рассмотреть различные показатели, такие как точность, оценка F1 и т. д.

SVM в Python и R

Метод подгонки в python просто обучает модель SVM на данных Xtrain и ytrain, которые были разделены. В частности, метод подгонки соберет данные в Xtrain и ytrain и на их основе рассчитает два опорных вектора.

Как только эти опорные векторы оценены, модель классификатора полностью настроена для создания новых прогнозов с помощью функции прогнозирования, поскольку ей нужны опорные векторы только для разделения новых данных. Теперь вы можете получить разные результаты в Python и в R, поэтому обязательно проверьте значение параметра seed.

Заключение

В этой статье мы подробно рассмотрели алгоритм машины опорных векторов. Спасибо за ваше время. Настройтесь на больше таких статей.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.

Для решения каких задач подходят модели машины опорных векторов?

Методы опорных векторов (SVM) лучше всего работают с линейно разделимыми данными, т. е. с данными, которые можно разделить на два отдельных класса с помощью прямой линии или гиперплоскости. Одним из наиболее распространенных применений SVM является распознавание лиц. Метод собственных лиц является примером SVM, который уменьшает размерность изображений лиц и используется для распознавания лиц. Этот метод основан на предположении, что лица можно рассматривать как векторы в многомерном векторном пространстве, а размерность уменьшается за счет подгонки к данным гиперсферы. Это позволяет нам сопоставлять две грани разного размера или повернутые. SVM также используется в классификации.

Каковы приложения SVM в реальной жизни?

Можно ли использовать SVM для непрерывных данных?

SVM используется для создания модели классификации. Итак, если у вас есть классификатор, он должен работать только с двумя классами. Если у вас есть непрерывные данные, вам придется превратить эти данные в классы, этот процесс называется уменьшением размерности. Например, если у вас есть что-то вроде возраста, роста, веса, класса и т. д., вы можете взять среднее значение этих данных и приблизить его к тому или иному классу, что облегчит классификацию.