サポートベクターマシン：SVMの種類[アルゴリズムの説明]

公開: 2020-12-01

序章

分類（決定ツリー、ランダムフォレスト、K-NN）と回帰のタスクを実行する機械学習の他のアルゴリズムと同様に、プール全体でそのようなアルゴリズムの1つであるサポートベクターマシンまたはSVMをサポートします。これは、分類または回帰のいずれかに関連する問題に使用される教師あり（ラベル付きデータセットが必要）の機械学習アルゴリズムです。

ただし、分類問題に頻繁に適用されます。 SVMアルゴリズムでは、各データ項目をポイントとしてプロットします。プロットはn次元空間で行われます。ここで、nは特定のデータの特徴の数です。次に、2つ（またはそれ以上）のクラスを効果的に分離する最適な超平面を見つけることによって分類が実行されます。

サポートベクターという用語は、個々の特徴の単なる座標です。なぜデータポイントをあなたが尋ねるかもしれないベクトルとして一般化するのか。実際の問題では、より高次元のデータセットが存在します。高次元（n次元）では、点と見なすよりも、ベクトル演算と行列操作を実行する方が理にかなっています。

SVMの種類

線形SVM：線形SVMは、線形分離可能なデータ、つまり1本の直線を利用して2つのカテゴリに分類できるデータセットに使用されます。 このようなデータポイントは線形分離可能データと呼ばれ、分類器は線形SVM分類器として説明されて使用されます。

非線形SVM：非線形SVMは、非線形に分離可能なデータであるデータに使用されます。つまり、データセットの分類に直線を使用することはできません。このために、平面または他の数学関数を使用してデータポイントを分離できる高次元にデータポイントを設定するカーネルトリックと呼ばれるものを使用します。このようなデータポイントは非線形データと呼ばれ、使用される分類器は非線形SVM分類器と呼ばれます。

線形SVMのアルゴリズム

バイナリ分類の問題について話しましょう。タスクは、いずれかのクラスのテストポイントを可能な限り正確に効率的に分類することです。以下は、SVMプロセスに関連する手順です。

まず、2つのクラスに属するポイントのセットが、以下に示すようにプロットおよび視覚化されます。 2次元空間では、直線を適用するだけで、これら2つのクラスを効率的に分割できます。しかし、これらのクラスを分類できる行はたくさんあります。選択できる線または超平面（緑色の線）のセットがあります。明らかな問題は、これらすべての行のうち、どの行が分類に適しているかということです。

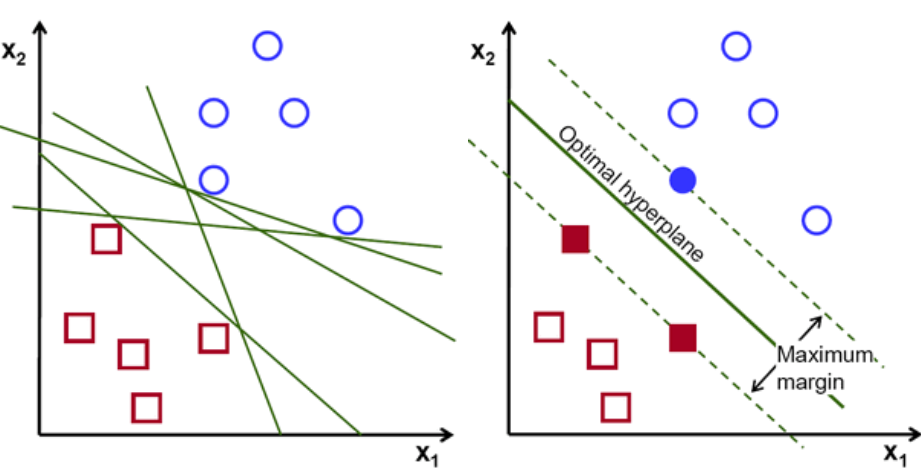
ハイパープレーンのセット、画像クレジット

基本的に、2つのクラスをより適切に分離する超平面を選択します。これを行うには、最も近いデータポイントと超平面の間の距離を最大化します。距離が大きいほど、超平面が良くなり、分類結果が良くなります。下の図から、選択した超平面が、これらの各クラスの最も近い点からの距離が最大であることがわかります。

各クラスの最も近い点を横切る超平面に平行な2本の点線は、超平面のサポートベクターと呼ばれます。ここで、サポートベクトルと超平面の間の分離距離はマージンと呼ばれます。また、SVMアルゴリズムの目的は、このマージンを最大化することです。最適な超平面は、最大マージンを持つ超平面です。

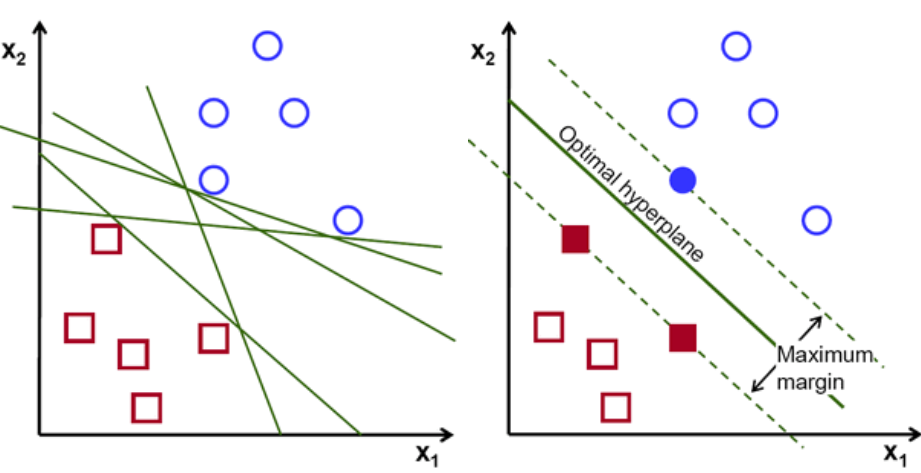
画像クレジット

たとえば、セルを良いものと悪いものに分類します。セルxᵢは、n次元空間にプロットできるこれらの特徴ベクトルのそれぞれは、クラスyᵢでラベル付けされています。 クラスyᵢは+veまたは-veのいずれかになります（例：good = 1、not good =-1）。 超平面の方程式はy= wx + b = 0です。ここで、Wとbはラインパラメータです。 前の式は、+ veクラスの例では≥1、-veクラスの例では≤-1の値を返します。

しかし、どのようにしてこの超平面を見つけるのでしょうか？ 超平面は、最適値wまたは重みおよびbまたは切片を見つけることによって定義されます。そして、これらの最適値は、コスト関数を最小化することによって見つけられます。アルゴリズムがこれらの最適値を収集すると、SVMモデルまたはライン関数f（x）が2つのクラスを効率的に分類します。

一言で言えば、最適な超平面の方程式はw.x + b=0です。左側のサポートベクターの方程式はw.x+b = -1で、右側のサポートベクターの方程式はw.x + b=1です。

したがって、2つの平行なリーエンAy = Bx+c1とAy=Bx + c2の間の距離dは、d = | C1–C2|/√A^2+B^2で与えられます。この式を使用すると、2つのサポートベクター間の距離は2 / ||w||になります。

SVMのコスト関数は次の式のようになります。

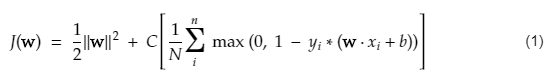
画像クレジット
SVM損失関数
上記のコスト関数方程式で、λパラメータは、λが大きいほどマージンが広くなり、λが小さいほどマージンが小さくなることを示します。さらに、コスト関数の勾配が計算され、失われた関数を下げる方向に重みが更新されます。

読む：機械学習の線形代数：重要な概念、MLの前に学ぶ理由
非線形SVMのアルゴリズム
SVM分類器では、これら2つのクラスの間に線形超平面を設定するのは簡単です。しかし、発生する興味深い質問は、データが線形分離可能でない場合、何をすべきかということです。このため、SVMアルゴリズムにはカーネルトリックと呼ばれる方法があります。
SVMカーネル関数は、低次元の入力空間を取り込み、それを高次元の空間に変換します。簡単に言えば、それは分離不可能な問題を分離可能な問題に変換します。ラベルまたはそれらを定義する出力に基づいて複雑なデータ変換を実行します
下の図を見て、データ変換をよりよく理解してください。左側のデータポイントのセットは、明らかに線形分離可能ではありません。しかし、関数Φをデータポイントのセットに適用すると、平面を介して分離可能な高次元の変換されたデータポイントが得られます。

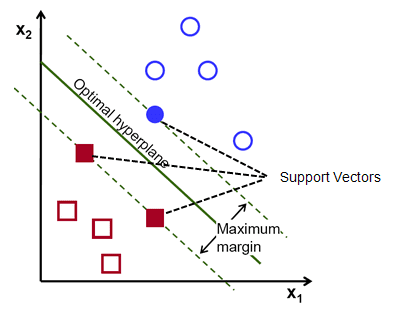
画像クレジット
線形分離不可能なデータポイントを分離するには、次元を追加する必要があります。線形データの場合、xとyの2つの次元が使用されています。これらのデータポイントに対して、3番目の次元（zなど）を追加します。以下の例では、z=x²+y²とします。
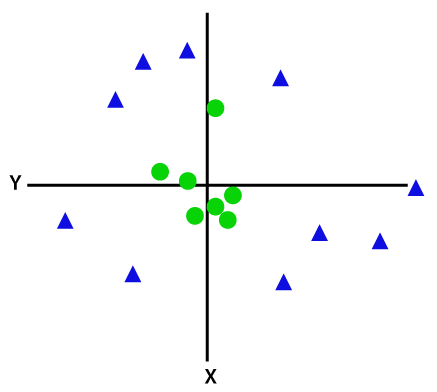
画像クレジット
このz関数または追加された次元はサンプル空間を変換し、上の画像は次のようになります。
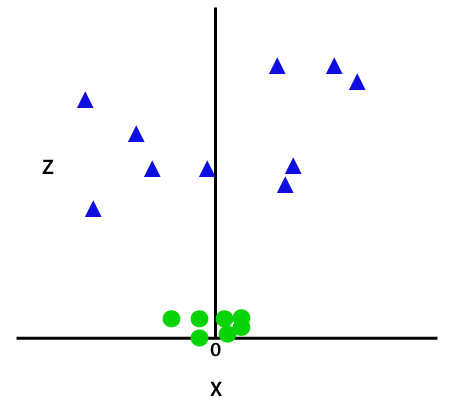
画像クレジット
綿密な分析では、上記のデータポイントは、x軸に平行であるか、ある角度で傾斜している直線関数を使用して分離できることが明らかです。線形、非線形、多項式、動径基底関数（RBF）、シグモイドなど、さまざまな種類のカーネル関数が存在します。

RBFが簡単に言うと、ある点を選択すると、RBFの結果は、その点とある固定点の間の距離のノルムになります。言い換えると、このRBFの歩留まりを使用してazディメンションを設計できます。これは通常、あるポイントからのポイントの距離に応じて「高さ」を示します。
チェックアウト：知っておく必要のあるニューラルネットワークの6種類の活性化関数
どのカーネルを選択しますか？
どのカーネルが最適かを判断するための優れた方法は、さまざまなカーネルを使用してさまざまなモデルを作成し、それぞれのパフォーマンスを推定して、最終的に結果を比較することです。次に、最良の結果が得られるカーネルを選択します。 K-Fold Cross-Validationを使用して、異なる観測値でのモデルのパフォーマンスを推定し、精度、F1スコアなどのさまざまなメトリックを検討するように特に注意してください。

PythonおよびRのSVM
Pythonのfitメソッドは、分離されたXtrainデータとytrainデータでSVMモデルをトレーニングするだけです。より具体的には、fitメソッドはXtrainとytrainのデータをアセンブルし、そこから2つのサポートベクターを計算します。
これらのサポートベクターが推定されると、分類器モデルは、新しいデータを分離するためのサポートベクターのみを必要とするため、predict関数を使用して新しい予測を生成するように完全に設定されます。これで、PythonとRで異なる結果が得られる可能性があるため、シードパラメータの値を必ず確認してください。
結論
この記事では、サポートベクターマシンアルゴリズムについて詳しく説明しました。御時間ありがとうございます。より多くのそのような記事に注目してください。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。
サポートベクターマシンモデルはどのような問題に適していますか？
サポートベクターマシン（SVM）は、線形分離可能なデータ、つまり直線または超平面を使用して2つの異なるクラスに分離できるデータで最適に機能します。 SVMの最も一般的な用途の1つは、顔認識です。固有顔技術は、顔画像の次元削減を行い、顔認識に使用されるSVMの例です。この手法は、面が高次元のベクトル空間内のベクトルと見なすことができ、データに超球を適合させることによって次元が減少するという前提に基づいています。これにより、サイズが異なる、または回転している2つの面を一致させることができます。 SVMは分類にも使用されます。
実際のSVMのアプリケーションは何ですか？
SVMは連続データに使用できますか？
SVMは、分類モデルを作成するために使用されます。したがって、分類子がある場合は、2つのクラスでのみ機能する必要があります。連続データがある場合は、そのデータをクラスに変換する必要があります。このプロセスは次元削減と呼ばれます。たとえば、年齢、身長、体重、学年などがある場合は、そのデータの平均を取り、それをあるクラスまたは別のクラスに近づけることができます。これにより、分類が容易になります。