دعم آلات المتجهات: أنواع SVM [شرح الخوارزمية]

مقدمة

تمامًا مثل الخوارزميات الأخرى في التعلم الآلي التي تؤدي مهمة التصنيف (أشجار القرار ، الغابة العشوائية ، K-NN) والانحدار ، دعم Vector Machine أو SVM أحد هذه الخوارزميات في المجموعة بأكملها. إنها خوارزمية تعلم آلي خاضعة للإشراف (تتطلب مجموعات بيانات مصنفة) تُستخدم للمشكلات المتعلقة إما بالتصنيف أو الانحدار.

ومع ذلك ، يتم تطبيقه بشكل متكرر في مشاكل التصنيف. تستلزم خوارزمية SVM رسم كل عنصر بيانات كنقطة. يتم التخطيط في فضاء ذو ​​أبعاد n حيث n هو عدد ميزات بيانات معينة. بعد ذلك ، يتم التصنيف من خلال إيجاد المستوي الفائق الأنسب الذي يفصل بين فئتين (أو أكثر) بشكل فعال.

مصطلح متجهات الدعم هو مجرد إحداثيات لميزة فردية. قد تسأل لماذا تعمم نقاط البيانات كنواقل. في مشاكل العالم الحقيقي ، توجد مجموعات بيانات ذات أبعاد أعلى. في الأبعاد الأعلى (البعد n) ، يكون من المنطقي إجراء العمليات الحسابية المتجهية ومعالجات المصفوفة بدلاً من اعتبارها نقاطًا.

أنواع SVM

SVM الخطي: يُستخدم SVM الخطي للبيانات التي يمكن فصلها خطيًا ، أي لمجموعة بيانات يمكن تصنيفها إلى فئتين باستخدام خط مستقيم واحد. تسمى نقاط البيانات هذه على أنها بيانات قابلة للفصل خطيًا ، ويتم استخدام المصنف كمصنف خطي SVM.

SVM غير الخطي: يُستخدم SVM غير الخطي للبيانات التي تكون بيانات غير قابلة للفصل خطيًا ، أي لا يمكن استخدام خط مستقيم لتصنيف مجموعة البيانات. لهذا ، نستخدم شيئًا يُعرف باسم خدعة النواة التي تحدد نقاط البيانات في بُعد أعلى حيث يمكن فصلها باستخدام المستويات أو الوظائف الرياضية الأخرى. تسمى نقاط البيانات هذه على أنها بيانات غير خطية ، ويطلق على المصنف المستخدم مصطلح مصنف SVM غير خطي.

خوارزمية لـ Linear SVM

لنتحدث عن مشكلة التصنيف الثنائي. وتتمثل المهمة في تصنيف نقطة اختبار بكفاءة في أي من الفئات بأكبر قدر ممكن من الدقة. فيما يلي الخطوات المتضمنة في عملية SVM.

أولاً ، مجموعة من النقاط التي تنتمي إلى الفئتين يتم رسمها وتصورها كما هو موضح أدناه. في مساحة ثنائية الأبعاد بتطبيق خط مستقيم ، يمكننا قسمة هاتين الفئتين بكفاءة. ولكن يمكن أن يكون هناك العديد من السطور التي يمكنها تصنيف هذه الفئات. هناك مجموعة من الخطوط أو المخططات التشعبية (خطوط خضراء) للاختيار من بينها. السؤال الواضح سيكون ، من بين كل هذه السطور ، أي خط مناسب للتصنيف؟

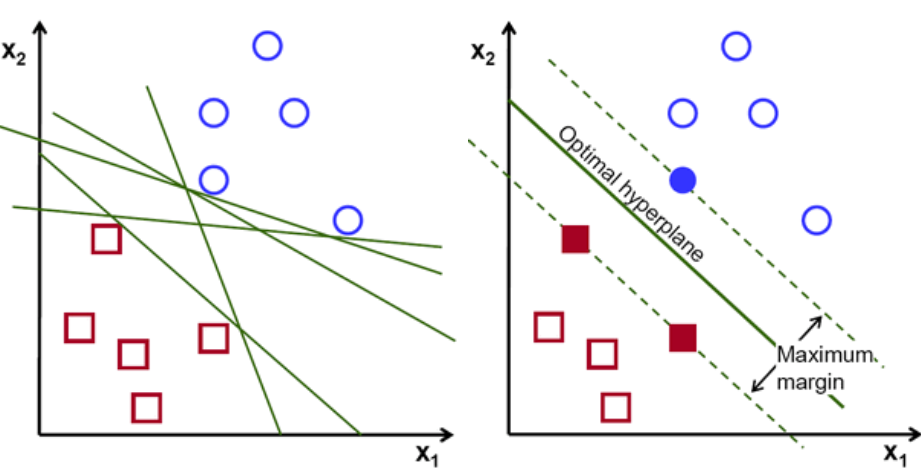
مجموعة من الطائرات الفائقة ، صورة الائتمان

بشكل أساسي ، حدد المستوى الفائق الذي يفصل بين الفئتين بشكل أفضل. نقوم بذلك عن طريق تعظيم المسافة بين أقرب نقطة بيانات والمستوى الفائق. وكلما زادت المسافة ، كان المستوى الفائق أفضل وتحقق نتائج تصنيف أفضل. يمكن أن نرى في الشكل أدناه أن الطائرة الفائقة المحددة لها أقصى مسافة من أقرب نقطة من كل فئة من هذه الفئات.

للتذكير ، يُشار إلى الخطين المنقطين اللذين يتوازيان مع المستوي الفائق الذي يعبر أقرب نقاط لكل فئة من الفئات باسم متجهات الدعم للطائرة الفائقة. الآن ، المسافة الفاصلة بين المتجهات الداعمة والمستوى الفائق تسمى الهامش. والغرض من خوارزمية SVM هو تعظيم هذا الهامش. المستوى الفائق الأمثل هو المستوى الفائق مع الحد الأقصى للهامش.

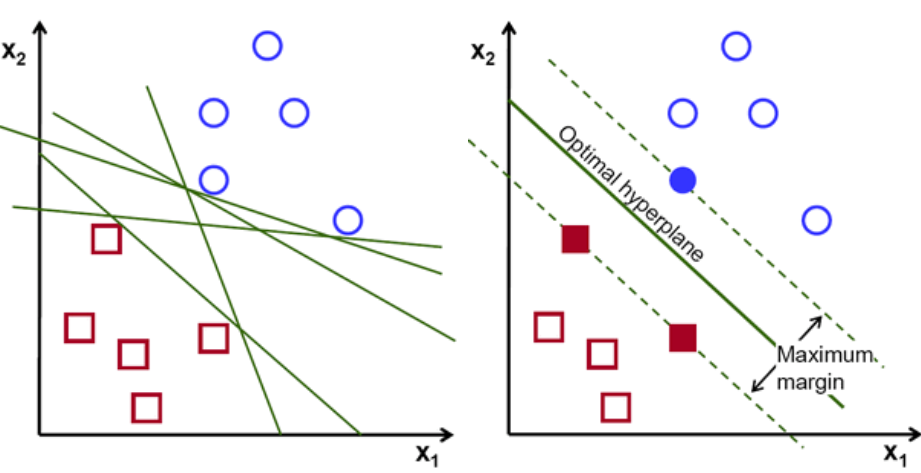
رصيد الصورة

خذ على سبيل المثال تصنيف الخلايا على أنها جيدة وسيئة. يتم تعريف الخلية xᵢ على أنها يتم تصنيف كل من ناقلات السمات هذه بفئة yᵢ. يمكن أن تكون الفئة yᵢ إما a + ve أو -ve (على سبيل المثال ، جيد = 1 ، ليس جيدًا = -1). معادلة المستوى الفائق هي y = wx + b = 0. حيث W و b معلمات خط. ترجع المعادلة السابقة قيمة ≥ 1 للحصول على أمثلة لفئة + ve و ≤-1 لأمثلة فئة.

لكن كيف تجد هذا المستوي الفائق؟ يتم تعريف المستوى الفائق من خلال إيجاد القيم المثلى w أو الأوزان و b أو التقاطع. ويتم العثور على هذه القيم المثلى عن طريق تقليل دالة التكلفة. بمجرد أن تجمع الخوارزمية هذه القيم المثلى ، يقوم نموذج SVM أو وظيفة الخط f (x) بتصنيف الفئتين بكفاءة.

باختصار ، المستوى الفائق الأمثل له المعادلة w.x + b = 0. متجه الدعم الأيسر له المعادلة w.x + b = -1 ومتجه الدعم الأيمن w.x + b = 1.

وبالتالي فإن المسافة d بين امتيازين متوازيين Ay = Bx + c1 و Ay = Bx + c2 تعطى بواسطة d = | C1 – C2 | / √A ^ 2 + B ^ 2. مع وضع هذه الصيغة في مكانها الصحيح ، لدينا المسافة بين متجهي الدعم كما يلي: 2 / || w ||.

تبدو دالة التكلفة لـ SVM مثل المعادلة أدناه:

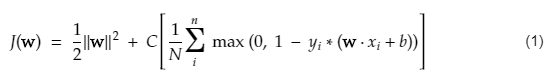
رصيد الصورة

وظيفة فقدان SVM

في معادلة دالة التكلفة أعلاه ، تشير المعلمة إلى أن الأكبر يوفر هامشًا أوسع ، وأن أصغر λ قد ينتج عنه هامش أصغر. علاوة على ذلك ، يتم حساب تدرج دالة التكلفة ويتم تحديث الأوزان في الاتجاه الذي يقلل من الوظيفة المفقودة.

اقرأ: الجبر الخطي لتعلم الآلة: المفاهيم الحاسمة ، لماذا نتعلم قبل تعلم الآلة

خوارزمية لـ SVM غير الخطي

في مصنف SVM ، من المستقيم أن يكون هناك مستوى خطي مفرط بين هاتين الفئتين. لكن السؤال المثير الذي يطرح نفسه هو ، ماذا لو لم تكن البيانات قابلة للفصل خطيًا ، فما الذي يجب فعله؟ لهذا ، تحتوي خوارزمية SVM على طريقة تسمى خدعة kernel.

تأخذ وظيفة نواة SVM مساحة إدخال منخفضة الأبعاد وتحولها إلى مساحة ذات أبعاد أعلى. بكلمات بسيطة ، فإنه يحول المشكلة غير القابلة للفصل إلى مشكلة قابلة للفصل. يقوم بإجراء تحويلات معقدة للبيانات بناءً على الملصقات أو المخرجات التي تحددها

انظر إلى الرسم التخطيطي أدناه لفهم تحويل البيانات بشكل أفضل. من الواضح أن مجموعة نقاط البيانات الموجودة على اليسار لا يمكن فصلها خطيًا. لكن عندما نطبق دالة Φ على مجموعة نقاط البيانات ، نحصل على نقاط بيانات محولة في بُعد أعلى يمكن فصله عبر مستوى.

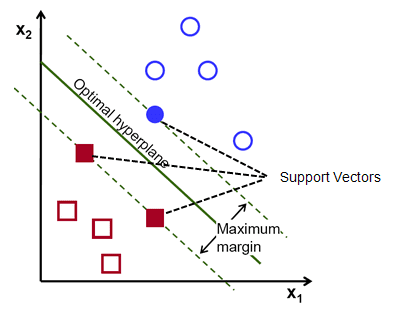
رصيد الصورة

لفصل نقاط البيانات غير القابلة للفصل خطيًا ، يتعين علينا إضافة بُعد إضافي. بالنسبة للبيانات الخطية ، تم استخدام بعدين ، أي x و y. بالنسبة إلى نقاط البيانات هذه ، نضيف بعدًا ثالثًا ، على سبيل المثال z. في المثال أدناه ، لنفترض أن z = x² + y².

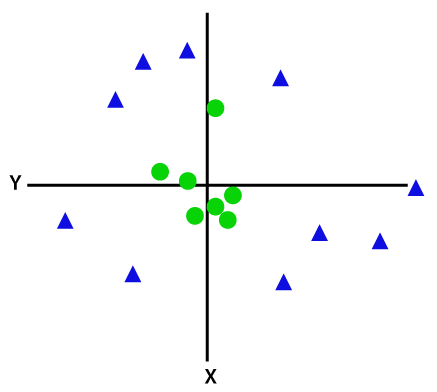
رصيد الصورة

تعمل هذه الوظيفة z أو الأبعاد المضافة على تحويل مساحة العينة وستصبح الصورة أعلاه على النحو التالي:

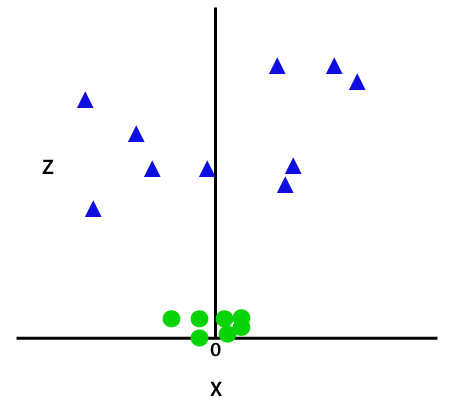
رصيد الصورة

عند التحليل الوثيق ، من الواضح أنه يمكن فصل نقاط البيانات أعلاه باستخدام دالة الخط المستقيم التي تكون إما موازية للمحور x أو تميل بزاوية. توجد أنواع مختلفة من وظائف النواة - دالة الأساس الخطية وغير الخطية ومتعددة الحدود والشعاعية (RBF) والسينية.

ما يفعله RBF بكلمات بسيطة هو - إذا اخترنا نقطة ما ، فستكون نتيجة RBF هي المعيار للمسافة بين تلك النقطة وبعض النقاط الثابتة. بعبارة أخرى ، يمكننا تصميم البعد من الألف إلى الياء مع عوائد هذا RBF ، والذي يعطي عادةً "الارتفاع" اعتمادًا على مدى بُعد النقطة عن نقطة ما.

تحقق من: 6 أنواع من وظائف التنشيط في الشبكات العصبية التي تحتاج إلى معرفتها

أي نواة تختار؟

هناك طريقة جيدة لتحديد النواة الأكثر ملاءمة وهي صنع نماذج مختلفة بنواة مختلفة ، ثم تقدير أداء كل منها ومقارنة النتائج في النهاية. ثم تختار النواة التي تحقق أفضل النتائج. كن خاصًا لتقدير أداء النموذج على عكس الملاحظات باستخدام التحقق من صحة K-Fold والنظر في مقاييس مختلفة مثل الدقة ، ودرجة F1 ، وما إلى ذلك.

SVM في Python و R.

تقوم طريقة الملاءمة في Python بتدريب نموذج SVM على بيانات Xtrain و ytrain التي تم فصلها. وبشكل أكثر تحديدًا ، ستجمع طريقة الملاءمة البيانات في Xtrain و ytrain ، ومن ذلك ستحسب متجهي الدعم.

بمجرد تقدير متجهات الدعم هذه ، يتم تعيين نموذج المصنف بالكامل لإنتاج تنبؤات جديدة مع وظيفة التنبؤ لأنه يحتاج فقط إلى متجهات الدعم لفصل البيانات الجديدة. الآن قد تحصل على نتائج مختلفة في Python و R ، لذا تأكد من التحقق من قيمة المعلمة الأولية.

خاتمة

في هذه المقالة ، نظرنا في خوارزمية Support Vector Machine بالتفصيل. شكرا على وقتك. قم بضبط المزيد من هذه المقالات.

إذا كنت مهتمًا بمعرفة المزيد حول التعلم الآلي ، فراجع دبلوم PG في IIIT-B & upGrad في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، IIIT- حالة الخريجين B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع أفضل الشركات.

ما أنواع المشكلات التي تفيدها نماذج Support Vector Machine؟

تعمل آلات المتجهات الداعمة (SVM) بشكل أفضل على البيانات القابلة للفصل خطيًا ، أي البيانات التي يمكن فصلها إلى فئتين متميزتين باستخدام خط مستقيم أو مستوي مفرط. يعد التعرف على الوجوه أحد الاستخدامات الأكثر شيوعًا لـ SVM. تقنية eigenfaces هي مثال على SVM ، والتي تعمل على تقليل أبعاد صور الوجه وتستخدم للتعرف على الوجوه. تعتمد هذه التقنية على فرضية أنه يمكن اعتبار الوجوه متجهات في فضاء متجه عالي الأبعاد ويتم تقليل الأبعاد عن طريق ملاءمة الغلاف الفائق للبيانات. هذا يسمح لنا بمطابقة وجهين بحجم مختلف أو تم تدويرهما. يستخدم SVM أيضًا في التصنيف.

ما هي تطبيقات SVMs في الحياة الواقعية؟

هل يمكن استخدام SVM للبيانات المستمرة؟

يستخدم SVM لإنشاء نموذج تصنيف. لذلك ، إذا كان لديك مصنف ، فيجب أن يعمل مع فصلين فقط. إذا كانت لديك بيانات مستمرة ، فسيتعين عليك تحويل تلك البيانات إلى فئات ، وتسمى العملية تقليل الأبعاد. على سبيل المثال ، إذا كان لديك شيء مثل العمر والطول والوزن والدرجة وما إلى ذلك ، فيمكنك أن تأخذ متوسط ​​تلك البيانات وتجعلها أقرب إلى فئة أو أخرى ، مما سيجعل التصنيف أسهل.