Máquinas de vetor de suporte: tipos de SVM [algoritmo explicado]

Introdução

Assim como outros algoritmos em aprendizado de máquina que realizam a tarefa de classificação (árvores de decisão, floresta aleatória, K-NN) e regressão, Support Vector Machine ou SVM um desses algoritmos em todo o pool. É um algoritmo de aprendizado de máquina supervisionado (requer conjuntos de dados rotulados) usado para problemas relacionados à classificação ou regressão.

No entanto, é frequentemente aplicado em problemas de classificação. O algoritmo SVM envolve a plotagem de cada item de dados como um ponto. A plotagem é feita em um espaço n-dimensional onde n é o número de características de um dado particular. Em seguida, a classificação é realizada encontrando o hiperplano mais adequado que separa as duas (ou mais) classes de forma eficaz.

O termo vetores de suporte são apenas coordenadas de um recurso individual. Por que generalizar pontos de dados como vetores, você pode perguntar. Em problemas do mundo real, existem conjuntos de dados de dimensões superiores. Em dimensões mais altas (dimensão n), faz mais sentido realizar manipulações aritméticas vetoriais e de matrizes do que considerá-las como pontos.

Tipos de SVM

Linear SVM : Linear SVM é usado para dados que são linearmente separáveis, ou seja, para um conjunto de dados que pode ser categorizado em duas categorias utilizando uma única linha reta. Esses pontos de dados são denominados como dados linearmente separáveis, e o classificador é usado descrito como um classificador SVM linear.

SVM não linear: SVM não linear é usado para dados que são dados não linearmente separáveis, ou seja, uma linha reta não pode ser usada para classificar o conjunto de dados. Para isso, usamos algo conhecido como um truque do kernel que define os pontos de dados em uma dimensão superior, onde eles podem ser separados usando planos ou outras funções matemáticas. Tais pontos de dados são denominados como dados não lineares, e o classificador usado é denominado como classificador SVM não linear.

Algoritmo para SVM Linear

Vamos falar sobre um problema de classificação binária. A tarefa é classificar eficientemente um ponto de teste em qualquer uma das classes com a maior precisão possível. A seguir estão as etapas envolvidas no processo SVM.

Primeiramente, um conjunto de pontos pertencentes às duas classes são plotados e visualizados como mostrado abaixo. Em um espaço 2-d apenas aplicando uma linha reta, podemos dividir eficientemente essas duas classes. Mas pode haver muitas linhas que podem classificar essas classes. Há um conjunto de linhas ou hiperplanos (linhas verdes) para escolher. A pergunta óbvia será, de todas essas linhas, qual linha é adequada para classificação?

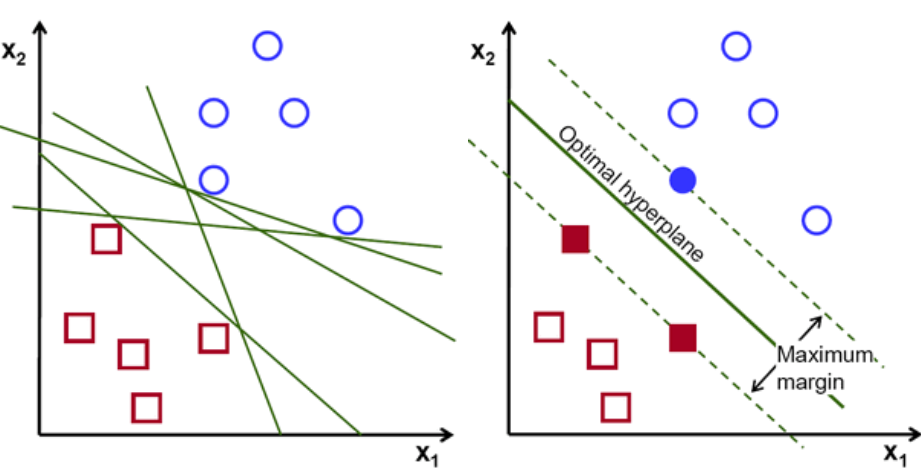
conjunto de hiperplanos, Crédito de imagem

Basicamente, selecione o hiperplano que separa melhor as duas classes. Fazemos isso maximizando a distância entre o ponto de dados mais próximo e o hiperplano. Quanto maior a distância, melhor é o hiperplano e melhores resultados de classificação resultam. Pode-se observar na figura abaixo que o hiperplano selecionado possui a distância máxima do ponto mais próximo de cada uma dessas classes.

Um lembrete, as duas linhas pontilhadas que vão paralelas ao hiperplano cruzando os pontos mais próximos de cada uma das classes são chamadas de vetores de suporte do hiperplano. Agora, a distância de separação entre os vetores de suporte e o hiperplano é chamada de margem. E o objetivo do algoritmo SVM é maximizar essa margem. O hiperplano ideal é o hiperplano com margem máxima.

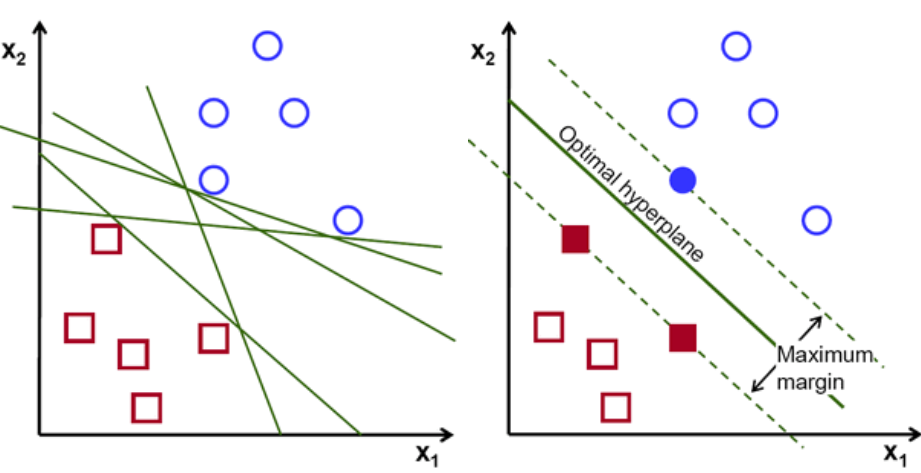
Crédito da imagem

Tomemos, por exemplo, classificar as células como boas e ruins. a célula xᵢ é definida como um Cada um desses vetores de características é rotulado com uma classe yᵢ. A classe yᵢ pode ser +ve ou -ve (por exemplo, bom=1, não bom =-1). A equação do hiperplano é y= wx + b = 0. Onde W e b são parâmetros de linha. A equação anterior retorna um valor ≥ 1 para exemplos de classe +ve e ≤-1 para exemplos de classe -ve.

Mas, como ele encontra esse hiperplano? O hiperplano é definido encontrando os valores ótimos w ou pesos e b ou interceptar qual. E esses valores ótimos são encontrados minimizando a função de custo. Uma vez que o algoritmo coleta esses valores ótimos, o modelo SVM ou a função de linha f(x) classifica eficientemente as duas classes.

Em poucas palavras, o hiperplano ótimo tem a equação w.x+b = 0. O vetor de suporte esquerdo tem a equação w.x+b=-1 e o vetor de suporte direito tem w.x+b=1.

Assim, a distância d entre duas linhas paralelas Ay = Bx + c1 e Ay = Bx + c2 é dada por d = |C1–C2|/√A^2 + B^2. Com esta fórmula em vigor, temos a distância entre os dois vetores de suporte como 2/||w||.

A função de custo para SVM se parece com a equação abaixo:

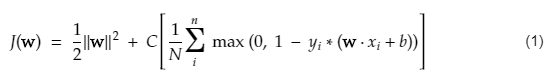
Crédito da imagem

Função de perda SVM

Na equação da função de custo acima, o parâmetro λ denota que um λ maior fornece uma margem mais ampla e um λ menor produziria uma margem menor. Além disso, o gradiente da função custo é calculado e os pesos são atualizados na direção que diminui a função perdida.

Leia: Álgebra linear para aprendizado de máquina: conceitos críticos, por que aprender antes de ML

Algoritmo para SVM não linear

No classificador SVM, é simples ter um hiperplano linear entre essas duas classes. Mas, uma questão interessante que surge é: e se os dados não forem linearmente separáveis, o que deve ser feito? Para isso, o algoritmo SVM possui um método chamado de truque do kernel.

A função do kernel SVM recebe um espaço de entrada de baixa dimensão e o converte em um espaço de dimensão mais alta. Em palavras simples, converte o problema não separável em um problema separável. Ele realiza transformações de dados complexas com base nos rótulos ou saídas que os definem

Veja o diagrama abaixo para entender melhor a transformação de dados. O conjunto de pontos de dados à esquerda claramente não é separável linearmente. Mas quando aplicamos uma função Φ ao conjunto de pontos de dados, obtemos pontos de dados transformados em uma dimensão superior que é separável por meio de um plano.

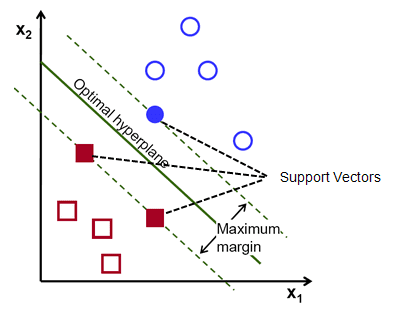
Crédito da imagem

Para separar pontos de dados não linearmente separáveis, temos que adicionar uma dimensão extra. Para dados lineares, foram utilizadas duas dimensões, ou seja, x e y. Para esses pontos de dados, adicionamos uma terceira dimensão, digamos z. Para o exemplo abaixo, seja z=x² +y².

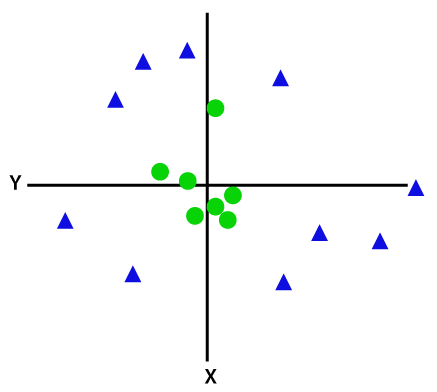
Crédito da imagem

Esta função z ou a dimensionalidade adicionada transforma o espaço amostral e a imagem acima se tornará a seguinte:

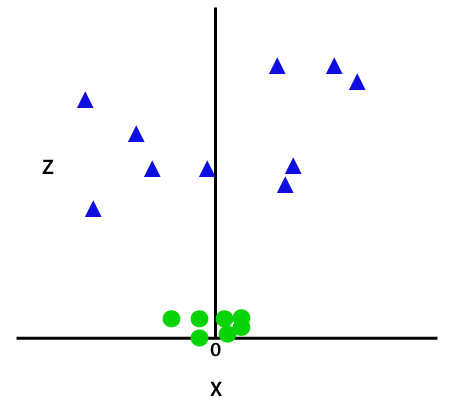
Crédito da imagem

Em uma análise mais detalhada, é evidente que os pontos de dados acima podem ser separados usando uma função de linha reta que é paralela ao eixo x ou inclinada em um ângulo. Diferentes tipos de funções de kernel estão presentes — linear, não linear, polinomial, função de base radial (RBF) e sigmóide.

O que o RBF faz em palavras simples é - se escolhermos algum ponto, o resultado de um RBF será a norma da distância entre esse ponto e algum ponto fixo. Em outras palavras, podemos projetar uma dimensão z com os rendimentos desse RBF, que normalmente fornece 'altura' dependendo de quão longe o ponto está de algum ponto.

Confira: 6 tipos de função de ativação em redes neurais que você precisa conhecer

Qual Kernel escolher?

Um bom método para determinar qual kernel é o mais adequado é fazer vários modelos com kernels variados, estimar o desempenho de cada um e, finalmente, comparar os resultados. Então você escolhe o kernel com os melhores resultados. Seja específico para estimar o desempenho do modelo em observações diferentes usando o K-Fold Cross-Validation e considere diferentes métricas como precisão, pontuação F1, etc.

SVM em Python e R

O método de ajuste em python simplesmente treina o modelo SVM nos dados Xtrain e ytrain que foram separados. Mais especificamente, o método de ajuste reunirá os dados em Xtrain e ytrain e, a partir disso, calculará os dois vetores de suporte.

Uma vez que esses vetores de suporte são estimados, o modelo classificador é completamente configurado para produzir novas previsões com a função de previsão, pois ele só precisa dos vetores de suporte para separar os novos dados. Agora você pode obter resultados diferentes em Python e em R, portanto, verifique o valor do parâmetro seed.

Conclusão

Neste artigo, analisamos o algoritmo Support Vector Machine em detalhes. Obrigado pelo seu tempo. Sintonize para mais artigos como este.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.

Para quais tipos de problemas os modelos Support Vector Machine são adequados?

Support Vector Machines (SVM) funcionam melhor em dados linearmente separáveis, ou seja, dados que podem ser separados em duas classes distintas usando uma linha reta ou hiperplano. Um dos usos mais comuns do SVM é no reconhecimento facial. A técnica de eigenfaces é um exemplo de SVM, que faz redução de dimensionalidade de imagens faciais e é utilizada para reconhecimento facial. Essa técnica é baseada na premissa de que as faces podem ser pensadas como vetores em um espaço vetorial de alta dimensão e a dimensionalidade é reduzida ajustando uma hiperesfera aos dados. Isso nos permite combinar duas faces que são de tamanhos diferentes ou são giradas. SVM também é usado na classificação.

Quais são as aplicações dos SVMs na vida real?

O SVM pode ser usado para dados contínuos?

SVM é usado para criar um modelo de classificação. Então, se você tem um classificador, ele tem que trabalhar com apenas duas classes. Se você tiver dados contínuos, terá que transformar esses dados em classes, o processo é chamado de redução de dimensionalidade. Por exemplo, se você tem algo como idade, altura, peso, série etc., então você pode pegar a média desses dados e aproximá-la de uma classe ou de outra, o que facilitará a classificação.