支持向量机：SVM 的类型 [算法解释]

已发表: 2020-12-01

介绍

就像机器学习中执行分类任务（决策树、随机森林、K-NN）和回归的其他算法一样，支持向量机或 SVM 是整个池中的一种此类算法。它是一种有监督的（需要标记数据集）机器学习算法，用于解决与分类或回归相关的问题。

但是，它经常应用于分类问题。 SVM 算法需要将每个数据项绘制为一个点。绘图是在 n 维空间中完成的，其中 n 是特定数据的特征数。然后，通过找到有效分离两个（或更多）类的最合适的超平面来进行分类。

术语支持向量只是单个特征的坐标。为什么将数据点概括为您可能会问的向量。在现实世界的问题中，存在更高维度的数据集。在更高维度（n 维度）中，执行向量算术和矩阵操作而不是将它们视为点更有意义。

支持向量机的类型

线性支持向量机：线性支持向量机用于线性可分的数据，即用于可以通过使用一条直线分为两类的数据集。 这样的数据点被称为线性可分数据，分类器被描述为线性 SVM 分类器。

非线性 SVM：非线性 SVM 用于非线性可分离数据的数据，即不能使用直线对数据集进行分类。 为此，我们使用了一种称为内核技巧的东西，将数据点设置在更高维度，可以使用平面或其他数学函数将它们分开。这样的数据点称为非线性数据，使用的分类器称为非线性 SVM 分类器。

线性 SVM 算法

让我们谈谈一个二元分类问题。任务是尽可能准确地对任一类中的测试点进行有效分类。以下是 SVM 过程中涉及的步骤。

首先，绘制和可视化属于这两个类的一组点，如下所示。在二维空间中，只需应用一条直线，我们就可以有效地划分这两个类。但是可以有很多行可以对这些类进行分类。有一组线或超平面（绿线）可供选择。显而易见的问题是，在所有这些行中，哪一行适合分类？

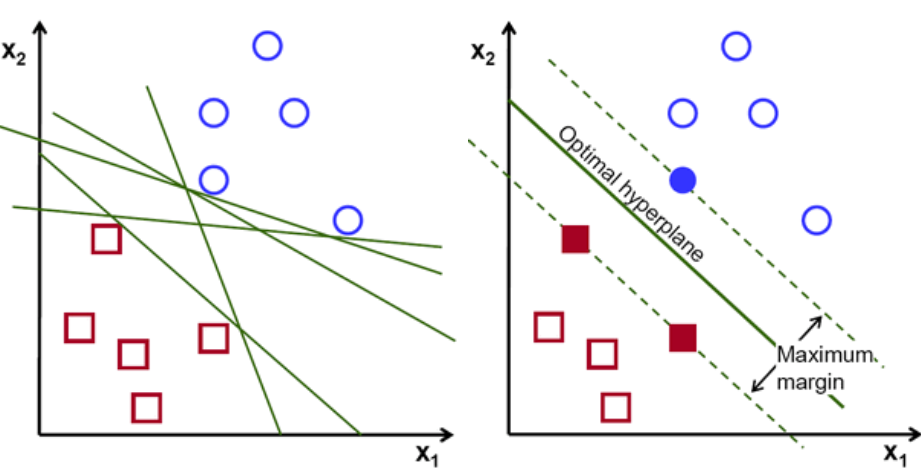
一组超平面，图片来源

基本上，选择能更好地分离这两个类的超平面。我们通过最大化最近数据点和超平面之间的距离来做到这一点。距离越大，超平面越好，从而得到更好的分类结果。从下图中可以看出，选择的超平面与每个类的最近点的距离最大。

提醒一下，平行于超平面穿过每个类的最近点的两条虚线称为超平面的支持向量。现在，支持向量和超平面之间的分离距离称为边距。而 SVM 算法的目的就是最大化这个余量。最优超平面是具有最大余量的超平面。

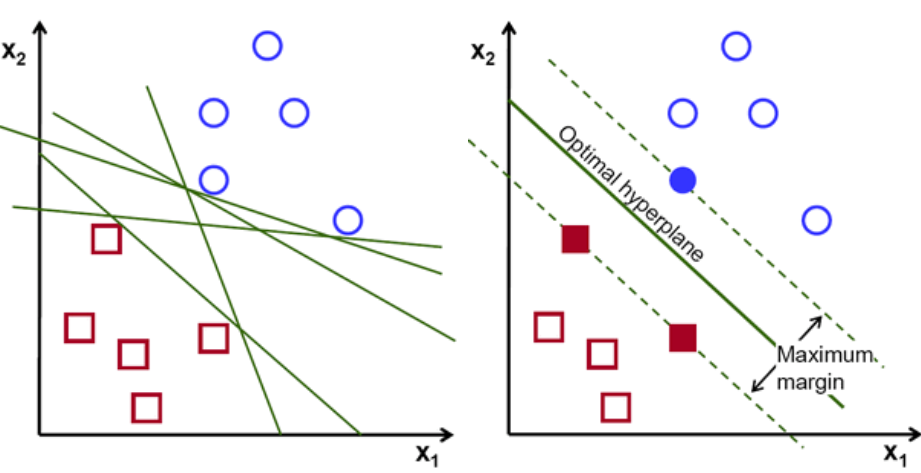
形象学分

以将细胞分类为好和坏为例。单元格xᵢ被定义为可以在 n 维空间上绘制的这些特征向量中的每一个都标有yᵢ 类。 yᵢ类可以是 +ve 或 -ve（例如，好=1，不好=-1）。 超平面的方程是 y= wx + b = 0。其中 W 和 b 是线参数。 对于 +ve 类的示例，前面的等式返回 ≥ 1 的值，对于 -ve 类的示例返回 ≤-1 的值。

但是，它是如何找到这个超平面的呢？ 超平面是通过找到最佳值 w 或权重和 b 或截距来定义的。这些最优值是通过最小化成本函数来找到的。一旦算法收集到这些最优值，SVM 模型或线函数 f(x) 就会有效地对这两个类别进行分类。

简而言之，最优超平面具有方程 w.x+b = 0。左支持向量具有方程 w.x+b=-1，右支持向量具有 w.x+b=1。

因此，两个平行留置权 Ay = Bx + c1 和 Ay = Bx + c2 之间的距离 d 由 d = |C1–C2|/√A^2 + B^2 给出。有了这个公式，我们就有两个支持向量之间的距离为 2/||w||。

SVM 的成本函数类似于以下等式：

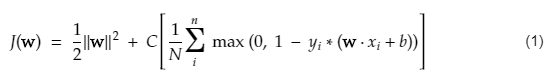
形象学分
SVM 损失函数
在上面的成本函数方程中，λ 参数表示较大的 λ 提供更宽的余量，较小的 λ 将产生较小的余量。此外，计算成本函数的梯度，并在降低损失函数的方向上更新权重。
阅读：机器学习的线性代数：关键概念，为什么要在机器学习之前学习

非线性 SVM 算法
在 SVM 分类器中，在这两个类之间有一个线性超平面是直截了当的。但是，一个有趣的问题是，如果数据不是线性可分的，该怎么办？为此，SVM 算法有一种称为核技巧的方法。
SVM 核函数接受低维输入空间并将其转换为高维空间。简而言之，它将不可分离的问题转换为可分离的问题。它根据定义它们的标签或输出执行复杂的数据转换
查看下图以更好地理解数据转换。左边的数据点集显然不是线性可分的。但是，当我们将函数 Φ 应用于数据点集时，我们会得到更高维度的转换数据点，该维度可通过平面分离。
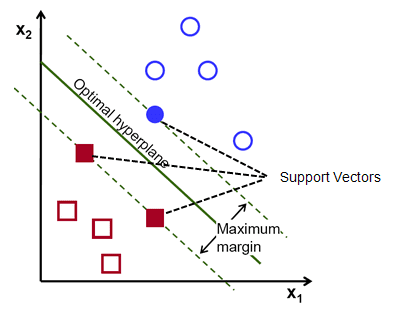
形象学分
为了分离非线性可分的数据点，我们必须添加一个额外的维度。对于线性数据，使用了两个维度，即 x 和 y。对于这些数据点，我们添加了第三个维度，比如 z。对于下面的示例，让 z=x² +y²。

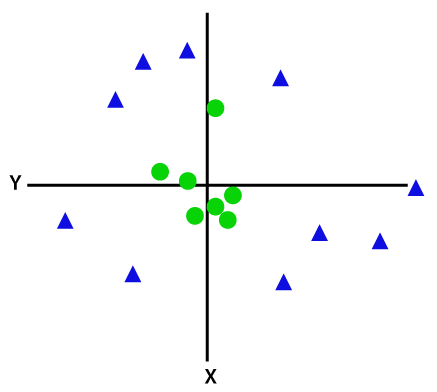
形象学分
这个 z 函数或添加的维度对样本空间进行变换，上图将变为如下：
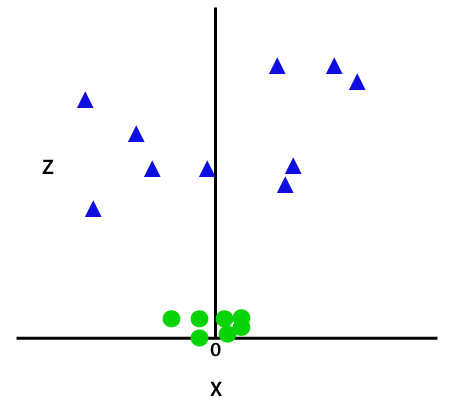
形象学分
仔细分析后，很明显，上述数据点可以使用平行于 x 轴或倾斜角度的直线函数分离。存在不同类型的核函数——线性、非线性、多项式、径向基函数 (RBF) 和 sigmoid。
简单来说，RBF 所做的是——如果我们选择某个点，RBF 的结果将是该点与某个固定点之间距离的范数。换句话说，我们可以用这个 RBF 的产量来设计 z 维度，它通常根据点与某个点的距离来给出“高度”。
查看：您需要了解的 6 种神经网络激活函数
选择哪个内核？
确定哪个内核最合适的一个好方法是制作具有不同内核的各种模型，然后估计它们的每个性能，并最终比较结果。然后你选择结果最好的内核。特别是通过使用 K-Fold 交叉验证来估计模型在不同观测值上的性能，并考虑不同的指标，如准确度、F1 分数等。

Python 和 R 中的 SVM
python 中的 fit 方法只是在已分离的 Xtrain 和 ytrain 数据上训练 SVM 模型。更具体地说，fit 方法将组合 Xtrain 和 ytrain 中的数据，并据此计算两个支持向量。
一旦估计了这些支持向量，分类器模型就完全设置为使用预测函数产生新的预测，因为它只需要支持向量来分离新数据。现在你可能在 Python 和 R 中得到不同的结果，所以一定要检查种子参数的值。
结论
在本文中，我们详细研究了支持向量机算法。谢谢你的时间。收看更多此类文章。
如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。

支持向量机模型适用于哪些类型的问题？
支持向量机 (SVM) 最适用于线性可分数据，即可以使用直线或超平面将数据分成两个不同的类别。 SVM 最常见的用途之一是人脸识别。 eigenfaces 技术是 SVM 的一个例子，它对面部图像进行降维并用于面部识别。该技术基于这样的前提，即人脸可以被认为是高维向量空间中的向量，并且通过将超球面拟合到数据来降低维数。这允许我们匹配两个不同大小或旋转的面。 SVM 也用于分类。
SVM在现实生活中有哪些应用？
SVM 可以用于连续数据吗？
SVM 用于创建分类模型。所以，如果你有一个分类器，它只能与两个类一起工作。如果你有连续的数据，那么你必须把这些数据变成类，这个过程称为降维。例如，如果您有年龄、身高、体重、年级等信息，那么您可以取该数据的平均值，使其更接近某一类或另一类，这将使分类更容易。