Supporta macchine vettoriali: tipi di SVM [spiegazione dell'algoritmo]

introduzione

Proprio come altri algoritmi nell'apprendimento automatico che svolgono il compito di classificazione (alberi decisionali, foresta casuale, K-NN) e regressione, Support Vector Machine o SVM uno di questi algoritmi nell'intero pool. È un algoritmo di apprendimento automatico supervisionato (richiede set di dati etichettati) utilizzato per problemi relativi alla classificazione o alla regressione.

Tuttavia, viene spesso applicato nei problemi di classificazione. L'algoritmo SVM prevede il tracciamento di ciascun elemento di dati come punto. Il tracciamento viene eseguito in uno spazio n-dimensionale dove n è il numero di caratteristiche di un dato particolare. Quindi, la classificazione viene effettuata trovando l'iperpiano più adatto che separi efficacemente le due (o più) classi.

Il termine vettori di supporto sono solo coordinate di una singola caratteristica. Perché generalizzare i punti dati come vettori potresti chiedere. Nei problemi del mondo reale esistono set di dati di dimensioni superiori. Nelle dimensioni superiori (n-dimensione), ha più senso eseguire manipolazioni aritmetiche vettoriali e matrici piuttosto che considerarle come punti.

Tipi di SVM

SVM lineare: SVM lineare viene utilizzato per dati separabili linearmente, ad esempio per un set di dati che può essere classificato in due categorie utilizzando un'unica linea retta. Tali punti dati sono definiti come dati separabili linearmente e il classificatore viene utilizzato descritto come classificatore SVM lineare.

SVM non lineare: SVM non lineare viene utilizzato per i dati che sono dati separabili in modo non lineare, ovvero non è possibile utilizzare una linea retta per classificare il set di dati. Per questo, utilizziamo qualcosa noto come un trucco del kernel che imposta i punti dati in una dimensione superiore in cui possono essere separati utilizzando piani o altre funzioni matematiche. Tali punti dati sono definiti come dati non lineari e il classificatore utilizzato è definito classificatore SVM non lineare.

Algoritmo per SVM lineare

Parliamo di un problema di classificazione binaria. Il compito è classificare in modo efficiente un punto di prova in una delle classi nel modo più accurato possibile. Di seguito sono riportati i passaggi coinvolti nel processo SVM.

In primo luogo, vengono tracciati e visualizzati gli insiemi di punti appartenenti alle due classi come mostrato di seguito. In uno spazio 2-d semplicemente applicando una linea retta, possiamo dividere in modo efficiente queste due classi. Ma ci possono essere molte linee che possono classificare queste classi. Ci sono una serie di linee o iperpiani (linee verdi) tra cui scegliere. La domanda ovvia sarà, tra tutte queste righe quale riga è adatta per la classificazione?

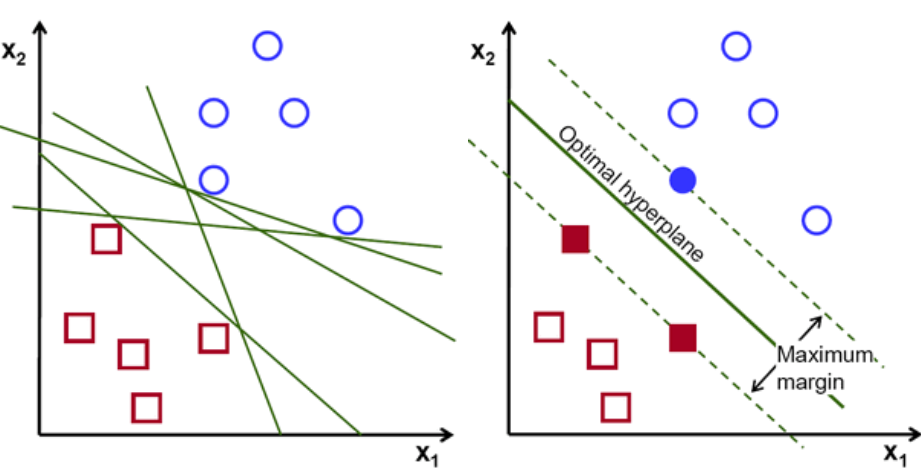
set di iperpiani, credito immagine

Fondamentalmente, seleziona l'iperpiano che separa meglio le due classi. Lo facciamo massimizzando la distanza tra il punto dati più vicino e l'iperpiano. Maggiore è la distanza, migliore è l'iperpiano e si ottengono migliori risultati di classificazione. Si può vedere nella figura sottostante che l'iperpiano selezionato ha la distanza massima dal punto più vicino da ciascuna di quelle classi.

Un promemoria, le due linee tratteggiate che vanno parallele all'iperpiano che attraversano i punti più vicini di ciascuna delle classi sono indicate come vettori di supporto dell'iperpiano. Ora, la distanza di separazione tra i vettori di supporto e l'iperpiano è chiamata margine. E lo scopo dell'algoritmo SVM è massimizzare questo margine. L'iperpiano ottimale è l'iperpiano con margine massimo.

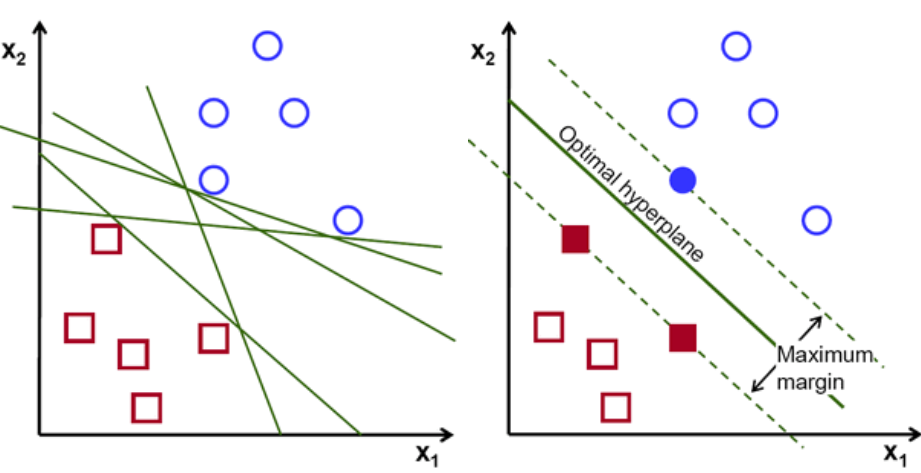
Credito immagine

Prendi ad esempio classificare le celle come buone e cattive. la cella xᵢ è definita come un Ciascuno di questi vettori di caratteristiche è etichettato con una classe yᵢ. La classe yᵢ può essere un +ve o -ve (es. buono=1, non buono =-1). L'equazione dell'iperpiano è y= wx + b = 0. Dove W e b sono parametri di linea. L'equazione precedente restituisce un valore ≥ 1 per esempi per la classe +ve e ≤-1 per gli esempi di classe -ve.

Ma come trova questo iperpiano? L'iperpiano è definito trovando i valori ottimali w o pesi e b o intercettare quali. E questi valori ottimali si trovano minimizzando la funzione di costo. Una volta che l'algoritmo ha raccolto questi valori ottimali, il modello SVM o la funzione di linea f(x) classifica in modo efficiente le due classi.

In poche parole, l'iperpiano ottimo ha l'equazione w.x+b = 0. Il vettore di supporto sinistro ha l'equazione w.x+b=-1 e il vettore di supporto destro ha w.x+b=1.

Quindi la distanza d tra due vincoli paralleli Ay = Bx + c1 e Ay = Bx + c2 è data da d = |C1–C2|/√A^2 + B^2. Con questa formula in atto, abbiamo la distanza tra i due vettori di supporto come 2/||w||.

La funzione di costo per SVM è simile all'equazione seguente:

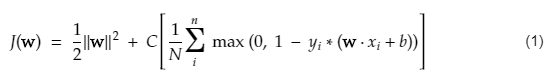
Credito immagine

Funzione di perdita SVM

Nell'equazione della funzione di costo sopra, il parametro λ denota che un λ più grande fornisce un margine più ampio e un λ più piccolo produrrebbe un margine più piccolo. Inoltre, viene calcolato il gradiente della funzione di costo e i pesi vengono aggiornati nella direzione che riduce la funzione persa.

Leggi: Algebra lineare per l'apprendimento automatico: concetti critici, perché imparare prima di ML

Algoritmo per SVM non lineare

Nel classificatore SVM, è semplice avere un iperpiano lineare tra queste due classi. Ma una domanda interessante che si pone è: cosa si dovrebbe fare se i dati non sono separabili linearmente? Per questo, l'algoritmo SVM ha un metodo chiamato trucco del kernel.

La funzione del kernel SVM occupa uno spazio di input di dimensioni ridotte e lo converte in uno spazio di dimensioni superiori. In parole semplici, converte il problema non separabile in un problema separabile. Esegue trasformazioni di dati complesse in base alle etichette o agli output che li definiscono

Guarda il diagramma seguente per comprendere meglio la trasformazione dei dati. L'insieme dei punti dati a sinistra non è chiaramente separabile in modo lineare. Ma quando applichiamo una funzione Φ all'insieme di punti dati, otteniamo punti dati trasformati in una dimensione superiore separabile tramite un piano.

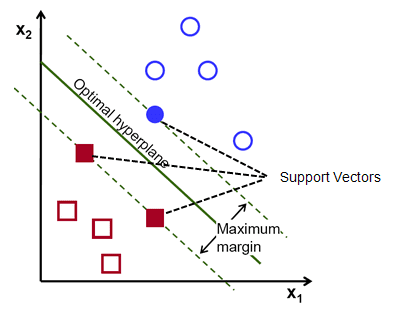
Credito immagine

Per separare punti dati non linearmente separabili, dobbiamo aggiungere una dimensione extra. Per i dati lineari sono state utilizzate due dimensioni, ovvero x e y. Per questi punti dati, aggiungiamo una terza dimensione, diciamo z. Per l'esempio seguente sia z=x² +y².

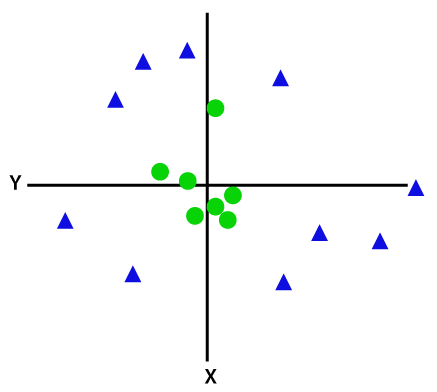
Credito immagine

Questa funzione z o la dimensionalità aggiunta trasforma lo spazio campione e l'immagine sopra diventerà la seguente:

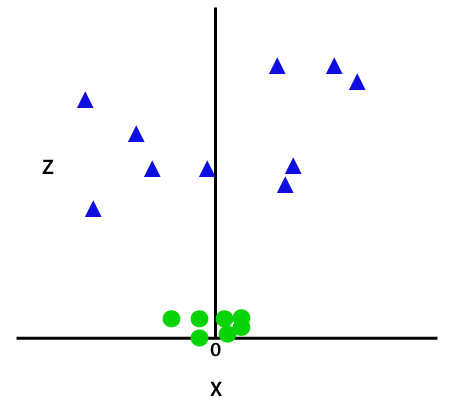
Credito immagine

A un'analisi ravvicinata, è evidente che i punti dati di cui sopra possono essere separati utilizzando una funzione di linea retta che è parallela all'asse x o è inclinata di un angolo. Sono presenti diversi tipi di funzioni del kernel: lineare, non lineare, polinomiale, funzione di base radiale (RBF) e sigmoide.

Ciò che RBF fa in parole semplici è: se scegliamo un punto, il risultato di un RBF sarà la norma della distanza tra quel punto e un punto fisso. In altre parole, possiamo progettare una dimensione z con i rendimenti di questo RBF, che in genere fornisce "altezza" a seconda di quanto è lontano il punto da un certo punto.

Dai un'occhiata: 6 tipi di funzione di attivazione nelle reti neurali che devi conoscere

Quale kernel scegliere?

Un buon metodo per determinare quale kernel è il più adatto è creare vari modelli con diversi kernel, quindi stimare ciascuna delle loro prestazioni e infine confrontare i risultati. Quindi scegli il kernel con i migliori risultati. Sii particolare nel stimare le prestazioni del modello su osservazioni diverse utilizzando la convalida incrociata K-Fold e considerare metriche diverse come Precisione, Punteggio F1, ecc.

SVM in Python e R

Il metodo fit in Python addestra semplicemente il modello SVM sui dati Xtrain e ytrain che sono stati separati. Più in particolare, il metodo fit assemblerà i dati in Xtrain e ytrain, e da quello, calcolerà i due vettori di supporto.

Una volta stimati questi vettori di supporto, il modello classificatore è completamente impostato per produrre nuove previsioni con la funzione di previsione perché ha bisogno solo dei vettori di supporto per separare i nuovi dati. Ora potresti ottenere risultati diversi in Python e in R, quindi assicurati di controllare il valore del parametro seed.

Conclusione

In questo articolo, abbiamo esaminato in dettaglio l'algoritmo Support Vector Machine. Grazie per il tuo tempo. Sintonizzati per altri articoli simili.

Se sei interessato a saperne di più sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, IIIT- B Status di Alumni, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.

Per quali tipi di problemi sono adatti i modelli Support Vector Machine?

Le Support Vector Machines (SVM) funzionano al meglio su dati separabili linearmente, cioè dati che possono essere separati in due classi distinte usando una linea retta o un iperpiano. Uno degli usi più comuni di SVM è il riconoscimento facciale. La tecnica eigenfaces è un esempio di SVM, che riduce la dimensionalità delle immagini facciali e viene utilizzata per il riconoscimento facciale. Questa tecnica si basa sulla premessa che i volti possono essere considerati vettori in uno spazio vettoriale ad alta dimensione e la dimensionalità viene ridotta adattando un'ipersfera ai dati. Questo ci consente di abbinare due facce di dimensioni diverse o ruotate. SVM viene utilizzato anche nella classificazione.

Quali sono le applicazioni delle SVM nella vita reale?

È possibile utilizzare SVM per dati continui?

SVM viene utilizzato per creare un modello di classificazione. Quindi, se hai un classificatore, deve funzionare solo con due classi. Se hai dati continui, dovrai trasformare quei dati in classi, il processo è chiamato riduzione della dimensionalità. Ad esempio, se hai qualcosa come età, altezza, peso, grado ecc., puoi prendere la media di quei dati e avvicinarli a una classe o all'altra, il che renderà più facile la classificazione.