서포트 벡터 머신: SVM의 유형 [알고리즘 설명]

게시 됨: 2020-12-01

소개

분류(의사결정 트리, 랜덤 포레스트, K-NN) 및 회귀 작업을 수행하는 머신 러닝의 다른 알고리즘과 마찬가지로 Support Vector Machine 또는 SVM은 전체 풀에서 이러한 알고리즘 중 하나입니다. 분류 또는 회귀와 관련된 문제에 사용되는 감독(레이블이 있는 데이터 세트 필요) 기계 학습 알고리즘입니다.

그러나 분류 문제에 자주 적용됩니다. SVM 알고리즘은 각 데이터 항목을 점으로 그리는 것을 수반합니다. 플로팅은 n차원 공간에서 수행되며 여기서 n은 특정 데이터의 특징 수입니다. 그런 다음 2개(또는 그 이상)의 클래스를 효과적으로 분리하는 가장 적합한 초평면을 찾아 분류를 수행합니다.

지지 벡터라는 용어는 개별 기능의 좌표일 뿐입니다. 데이터 포인트를 벡터로 일반화하는 이유는 무엇입니까? 실제 문제에는 더 높은 차원의 데이터 세트가 있습니다. 고차원(n차원)에서는 벡터 산술 및 행렬 조작을 점으로 간주하기보다 수행하는 것이 더 합리적입니다.

SVM의 유형

선형 SVM : 선형 SVM은 선형으로 분리 가능한 데이터, 즉 단일 직선을 활용하여 두 가지 범주로 분류할 수 있는 데이터 세트에 사용됩니다. 이러한 데이터 포인트를 선형 분리 가능한 데이터라고 하며 분류기를 Linear SVM 분류기로 설명하여 사용합니다.

비선형 SVM: 비선형 SVM 은 비선형적으로 분리 가능한 데이터인 데이터에 사용됩니다. 즉, 데이터 세트를 분류하는 데 직선을 사용할 수 없습니다. 이를 위해 우리는 평면이나 다른 수학 함수를 사용하여 분리할 수 있는 더 높은 차원에서 데이터 포인트를 설정하는 커널 트릭으로 알려진 것을 사용합니다. 이러한 데이터 포인트를 비선형 데이터라고 하며 사용된 분류기를 비선형 SVM 분류기라고 합니다.

선형 SVM을 위한 알고리즘

이진 분류 문제에 대해 이야기해 봅시다. 작업은 클래스 중 하나의 테스트 포인트를 가능한 한 정확하게 효율적으로 분류하는 것입니다. 다음은 SVM 프로세스와 관련된 단계입니다.

먼저 두 클래스에 속하는 점들의 집합을 다음과 같이 플로팅하고 시각화한다. 2차원 공간에서 직선을 적용하면 이 두 클래스를 효율적으로 나눌 수 있습니다. 그러나 이러한 클래스를 분류할 수 있는 라인이 많이 있을 수 있습니다. 선택할 수 있는 일련의 선 또는 초평면(녹색 선)이 있습니다. 분명한 질문은 이 모든 라인 중에서 어떤 라인이 분류에 적합한가 하는 것입니다.

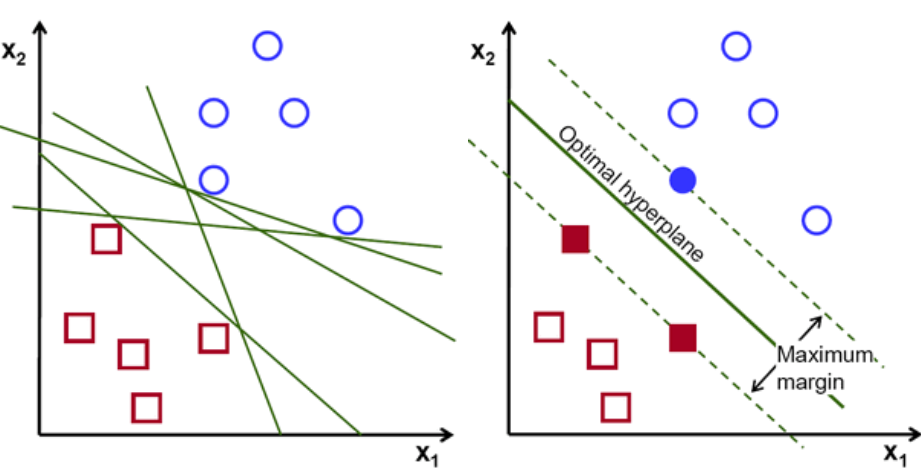
초평면 세트, 이미지 크레디트

기본적으로 두 클래스를 더 잘 구분하는 초평면을 선택합니다. 가장 가까운 데이터 포인트와 초평면 사이의 거리를 최대화하여 이를 수행합니다. 거리가 멀수록 초평면이 더 좋고 더 나은 분류 결과가 나옵니다. 아래 그림에서 선택한 초평면이 각 클래스에서 가장 가까운 점으로부터 최대 거리를 가짐을 알 수 있습니다.

각 클래스의 가장 가까운 점을 가로지르는 초평면에 평행하게 가는 두 개의 점선을 초평면의 지지 벡터라고 합니다. 이제 지지 벡터와 초평면 사이의 분리 거리를 마진이라고 합니다. 그리고 SVM 알고리즘의 목적은 이 마진을 최대화하는 것입니다. 최적의 초평면은 마진이 최대인 초평면입니다.

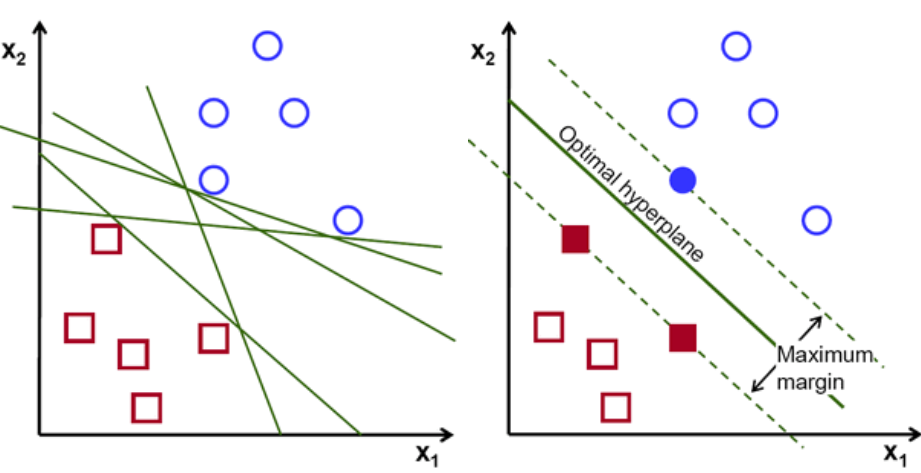
이미지 크레딧

예를 들어 세포를 좋은 것과 나쁜 것으로 분류합니다. 셀 xᵢ 는 n차원 공간에 표시할 수 있는 이러한 특징 벡터는 각각 yᵢ 클래스로 레이블이 지정됩니다. yᵢ 클래스 는 +ve 또는 -ve일 수 있습니다(예: good=1, not good =-1). 초평면의 방정식은 y= wx + b = 0입니다. 여기서 W와 b는 선 매개변수입니다. 앞의 방정식 은 +ve 클래스의 경우 ≥ 1 값을 반환하고 -ve 클래스의 경우 ≤-1 값을 반환합니다.

그러나 이 초평면은 어떻게 찾습니까? 초평면은 최적 값 w 또는 weights 및 b 또는 intercept를 찾는 것으로 정의됩니다. 그리고 이러한 최적값은 비용 함수를 최소화하여 찾습니다. 알고리즘이 이러한 최적 값을 수집하면 SVM 모델 또는 선 함수 f(x)가 두 클래스를 효율적으로 분류합니다.

간단히 말해서 최적의 초평면은 w.x+b = 0 방정식입니다. 왼쪽 지지 벡터는 w.x+b=-1 방정식이고 오른쪽 지지 벡터는 w.x+b=1입니다.

따라서 두 평행 선취권 Ay = Bx + c1 및 Ay = Bx + c2 사이의 거리 d는 d = |C1–C2|/√A^2 + B^2로 표시됩니다. 이 공식을 사용하면 두 지지 벡터 사이의 거리가 2/||w||입니다.

SVM의 비용 함수는 아래 방정식과 같습니다.

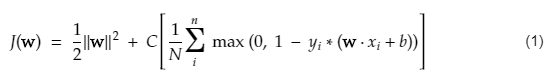
이미지 크레딧
SVM 손실 함수
위의 비용 함수 방정식에서 λ 매개변수는 λ가 클수록 더 넓은 마진을 제공하고 λ가 작을수록 더 작은 마진을 생성함을 나타냅니다. 또한, 비용 함수의 기울기를 계산하고 손실 함수를 낮추는 방향으로 가중치를 업데이트합니다.

읽기: 기계 학습을 위한 선형 대수학: 중요 개념, ML 전에 배워야 하는 이유
비선형 SVM 알고리즘
SVM 분류기에서 이 두 클래스 사이에 선형 초평면을 갖는 것은 간단합니다. 그러나 발생하는 흥미로운 질문은 데이터가 선형으로 분리할 수 없는 경우 어떻게 해야 합니까? 이를 위해 SVM 알고리즘에는 커널 트릭이라는 방법이 있습니다.
SVM 커널 함수는 저차원 입력 공간을 가져와 고차원 공간으로 변환합니다. 간단히 말해서 분리할 수 없는 문제를 분리할 수 있는 문제로 변환합니다. 이를 정의하는 레이블 또는 출력을 기반으로 복잡한 데이터 변환을 수행합니다.

데이터 변환을 더 잘 이해하려면 아래 다이어그램을 보십시오. 왼쪽의 데이터 포인트 세트는 분명히 선형으로 분리할 수 없습니다. 그러나 함수 Φ를 데이터 포인트 세트에 적용하면 평면을 통해 분리할 수 있는 더 높은 차원에서 변환된 데이터 포인트를 얻을 수 있습니다.
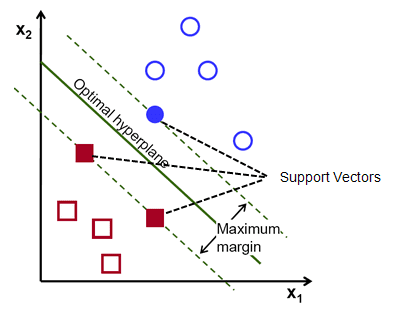
이미지 크레딧
선형으로 분리할 수 없는 데이터 요소를 분리하려면 차원을 추가해야 합니다. 선형 데이터의 경우 x와 y의 두 차원이 사용되었습니다. 이러한 데이터 포인트에 대해 z와 같은 세 번째 차원을 추가합니다. 아래 예의 경우 z=x² +y²로 설정합니다.
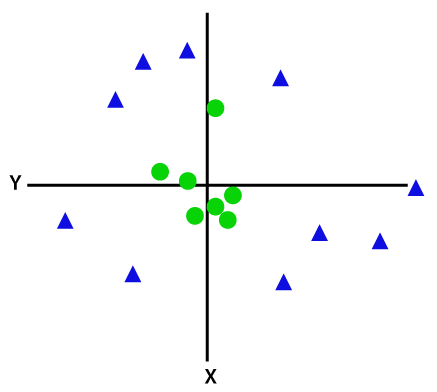
이미지 크레딧

이 z 함수 또는 추가된 차원은 샘플 공간을 변환하고 위의 이미지는 다음과 같이 됩니다.
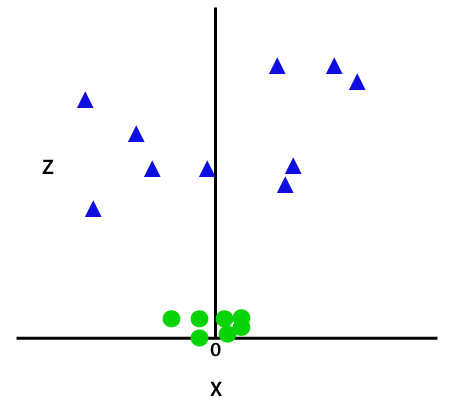
이미지 크레딧
면밀한 분석에서 위의 데이터 포인트는 x축에 평행하거나 비스듬히 기울어진 직선 함수를 사용하여 분리할 수 있음이 분명합니다. 선형, 비선형, 다항식, 방사형 기저 함수(RBF) 및 시그모이드와 같은 다양한 유형의 커널 함수가 있습니다.
간단히 말해서 RBF가 하는 일은 — 우리가 어떤 점을 고른다면, RBF의 결과는 그 점과 어떤 고정된 점 사이의 거리의 규범이 될 것입니다. 즉, 이 RBF의 수율로 az 차원을 설계할 수 있습니다. 이 RBF는 일반적으로 점이 특정 지점에서 얼마나 멀리 떨어져 있는지에 따라 '높이'를 제공합니다.

확인: 신경망에서 알아야 할 6가지 유형의 활성화 기능
어떤 커널을 선택해야 할까요?
어떤 커널이 가장 적합한지 결정하는 좋은 방법은 다양한 커널로 다양한 모델을 만든 다음 각각의 성능을 추정하고 궁극적으로 결과를 비교하는 것입니다. 그런 다음 최상의 결과를 가진 커널을 선택합니다. 특히 K-Fold 교차 검증을 사용하여 다른 관찰에 대한 모델의 성능을 추정하고 정확도, F1 점수 등과 같은 다양한 메트릭을 고려하십시오.
Python 및 R의 SVM
python의 fit 방법은 단순히 분리된 Xtrain 및 ytrain 데이터에 대해 SVM 모델을 훈련합니다. 보다 구체적으로, fit 방법은 Xtrain과 ytrain의 데이터를 조합하고, 그로부터 두 개의 지지 벡터를 계산합니다.
이러한 지원 벡터가 추정되면 분류기 모델은 새로운 데이터를 분리하기 위해 지원 벡터만 필요하기 때문에 예측 기능으로 새로운 예측을 생성하도록 완전히 설정됩니다. 이제 Python과 R에서 다른 결과를 얻을 수 있으므로 seed 매개변수의 값을 확인하십시오.
결론
이 기사에서는 Support Vector Machine 알고리즘에 대해 자세히 살펴보았습니다. 시간 내 줘서 고마워. 더 많은 기사를 시청하십시오.
기계 학습에 대해 자세히 알아보려면 IIIT-B 및 upGrad의 기계 학습 및 AI PG 디플로마를 확인하세요. 이 PG 디플로마는 일하는 전문가를 위해 설계되었으며 450시간 이상의 엄격한 교육, 30개 이상의 사례 연구 및 과제, IIIT- B 동문 자격, 5개 이상의 실용적인 실습 캡스톤 프로젝트 및 최고의 기업과의 취업 지원.
Support Vector Machine 모델은 어떤 문제에 적합합니까?
SVM(Support Vector Machines)은 선형으로 분리 가능한 데이터, 즉 직선 또는 초평면을 사용하여 두 개의 개별 클래스로 분리할 수 있는 데이터에서 가장 잘 작동합니다. SVM의 가장 일반적인 용도 중 하나는 얼굴 인식입니다. 고유얼굴 기법은 SVM의 한 예로서 얼굴 이미지의 차원 축소를 수행하고 얼굴 인식에 사용됩니다. 이 기술은 면을 고차원 벡터 공간에서 벡터로 생각할 수 있고 데이터에 초구(hypersphere)를 맞추면 차원이 축소된다는 전제에 기반합니다. 이를 통해 크기가 다르거나 회전된 두 면을 일치시킬 수 있습니다. SVM은 분류에도 사용됩니다.
실생활에서 SVM의 응용 프로그램은 무엇입니까?
연속 데이터에 SVM을 사용할 수 있습니까?
SVM은 분류 모델을 만드는 데 사용됩니다. 따라서 분류기가 있는 경우 두 개의 클래스에서만 작동해야 합니다. 연속 데이터가 있는 경우 해당 데이터를 클래스로 변환해야 하며 이 프로세스를 차원 축소라고 합니다. 예를 들어 나이, 키, 체중, 학년 등과 같은 항목이 있는 경우 해당 데이터의 평균을 가져와 한 클래스 또는 다른 클래스에 더 가깝게 만들 수 있습니다. 그러면 분류가 더 쉬워집니다.