Cigüeña, Parte 2: Creación de un analizador de expresiones
Publicado: 2022-03-11En esta parte de nuestra serie, cubriremos uno de los componentes más complicados (al menos en mi opinión) de la creación de secuencias de comandos de un motor de lenguaje, que es un bloque de construcción esencial para cada lenguaje de programación: el analizador de expresiones.
Una pregunta que un lector podría hacer, y con razón, es: ¿Por qué no usamos simplemente algunas herramientas o bibliotecas sofisticadas, algo que ya está a nuestra disposición?
¿Por qué no usamos Lex, YACC, Bison, Boost Spirit o al menos expresiones regulares?
A lo largo de nuestra relación, mi esposa ha notado un rasgo mío que no puedo negar: siempre que me enfrento a una pregunta difícil, hago una lista. Si lo piensa, tiene mucho sentido: estoy usando la cantidad para compensar la falta de calidad en mi respuesta.
Voy a hacer lo mismo ahora.
- Quiero usar C++ estándar. En este caso, será C++17. Creo que el lenguaje es bastante rico por sí solo, y estoy luchando contra la tentación de agregar algo que no sea la biblioteca estándar a la mezcla.
- Cuando desarrollé mi primer lenguaje de secuencias de comandos, no usé ninguna herramienta sofisticada. Estaba bajo presión y con un plazo ajustado, pero no sabía cómo usar Lex, YACC o algo similar. Por lo tanto, decidí desarrollar todo manualmente.
- Más tarde, encontré un blog de un desarrollador de lenguajes de programación experimentado, que desaconsejó el uso de cualquiera de estas herramientas. Dijo que esas herramientas resuelven la parte más fácil del desarrollo del lenguaje, por lo que, en cualquier caso, te quedan las cosas difíciles. No puedo encontrar ese blog en este momento, ya que fue hace mucho tiempo, cuando tanto Internet como yo éramos jóvenes.
- Al mismo tiempo, había un meme que decía: “Tienes un problema que decides resolver usando expresiones regulares. Ahora tienes dos problemas.
- No conozco a Lex, YACC, Bison ni nada parecido. Conozco Boost Spirit, y es una biblioteca útil y asombrosa, pero aun así prefiero tener un mejor control sobre el analizador.
- Me gusta hacer esos componentes manualmente. En realidad, podría dar esta respuesta y eliminar esta lista por completo.
El código completo está disponible en mi página de GitHub.
Iterador de tokens
Hay algunos cambios en el código de la Parte 1.
En su mayoría, se trata de arreglos simples y pequeños cambios, pero una adición importante al código de análisis existente es la clase token_iterator . Nos permite evaluar el token actual sin eliminarlo de la transmisión, lo cual es realmente útil.
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; Se inicializa con push_back_stream y luego se puede desreferenciar e incrementar. Se puede verificar con conversión bool explícita, que se evaluará como falso cuando el token actual sea igual a eof.
¿Lenguaje escrito estáticamente o dinámicamente?
Hay una decisión que tengo que tomar en esta parte: ¿Este lenguaje se escribirá estática o dinámicamente?
Un lenguaje tipado estáticamente es un lenguaje que verifica los tipos de sus variables en el momento de la compilación.
Un lenguaje de tipo dinámico , por otro lado, no lo verifica durante la compilación (si hay una compilación, que no es obligatoria para un lenguaje de tipo dinámico), sino durante la ejecución. Por lo tanto, los errores potenciales pueden permanecer en el código hasta que se detectan.
Esta es una ventaja obvia de los lenguajes tipificados estáticamente. A todo el mundo le gusta detectar sus errores lo antes posible. Siempre me pregunté cuál es la mayor ventaja de los lenguajes escritos dinámicamente, y la respuesta me llamó la atención en las últimas semanas: ¡es mucho más fácil de desarrollar!
El lenguaje anterior que desarrollé se tipeaba dinámicamente. Estaba más o menos satisfecho con el resultado, y escribir el analizador de expresiones no fue demasiado difícil. Básicamente, no tiene que verificar los tipos de variables y confía en los errores de tiempo de ejecución, que codifica casi espontáneamente.
Por ejemplo, si tiene que escribir el operador binario + y quiere hacerlo para números, solo necesita evaluar ambos lados de ese operador como números en el tiempo de ejecución. Si cualquiera de los lados no puede evaluar el número, simplemente lanza una excepción. Incluso implementé la sobrecarga de operadores al verificar la información de tipo de tiempo de ejecución de las variables en una expresión, y los operadores eran parte de esa información de tiempo de ejecución.
En el primer lenguaje que desarrollé (este es el tercero), hice una verificación de tipo en el momento de la compilación, pero no lo aproveché al máximo. La evaluación de la expresión todavía dependía de la información del tipo de tiempo de ejecución.
Ahora, decidí desarrollar un lenguaje tipado estáticamente y resultó ser una tarea mucho más difícil de lo esperado. Sin embargo, dado que no planeo compilarlo en un binario, o cualquier tipo de código ensamblador emulado, algún tipo de información existirá implícitamente en el código compilado.
Tipos
Como un mínimo de tipos que tenemos que admitir, comenzaremos con los siguientes:
- Números
- Instrumentos de cuerda
- Funciones
- arreglos
Aunque podemos agregarlos en el futuro, no admitiremos estructuras (o clases, registros, tuplas, etc.) al principio. Sin embargo, tendremos en cuenta que es posible que las agreguemos más adelante, por lo que no sellaremos nuestro destino con decisiones difíciles de cambiar.
Primero, quería definir el tipo como una cadena, que seguirá alguna convención. Cada identificador mantendría esa cadena por valor en el momento de la compilación, y tendremos que analizarla algunas veces. Por ejemplo, si codificamos el tipo de matriz de números como "[número]", tendremos que recortar el primer y el último carácter para obtener un tipo interno, que es "número" en este caso. Es una idea bastante mala si lo piensas.
Luego, traté de implementarlo como una clase. Esa clase tendría toda la información sobre el tipo. Cada identificador mantendría un puntero compartido a esa clase. Al final, pensé en tener el registro de todos los tipos utilizados durante la compilación, de modo que cada identificador tuviera el puntero sin formato a su tipo.
Me gustó la idea, así que terminamos con lo siguiente:
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;Los tipos simples son miembros de la enumeración:
enum struct simple_type { nothing, number, string, }; El miembro de enumeración nothing está aquí como marcador de posición para void , que no puedo usar porque es una palabra clave en C++.
Los tipos de matriz se representan con la estructura que tiene el único miembro de type_handle .
struct array_type { type_handle inner_type_id; }; Obviamente, la longitud de la matriz no forma parte de array_type , por lo que las matrices crecerán dinámicamente. Eso significa que terminaremos con std::deque o algo similar, pero nos ocuparemos de eso más adelante.
Un tipo de función se compone de su tipo de devolución, el tipo de cada uno de sus parámetros y si cada uno de esos parámetros se pasa o no por valor o por referencia.
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };Ahora, podemos definir la clase que mantendrá esos tipos.
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; Los tipos se mantienen en std::set , ya que ese contenedor es estable, lo que significa que los punteros a sus miembros son válidos incluso después de que se inserten nuevos tipos. Existe la función get_handle , que registra el tipo pasado y le devuelve el puntero. Si el tipo ya está registrado, devolverá el puntero al tipo existente. También hay funciones de conveniencia para obtener tipos primitivos.
En cuanto a la conversión implícita entre tipos, los números se convertirán en cadenas. No debería ser peligroso, ya que no es posible una conversión inversa, y el operador para la concatenación de cadenas es distinto al de la suma de números. Incluso si esa conversión se elimina en las últimas etapas del desarrollo de este lenguaje, servirá como ejercicio en este punto. Para ello, tuve que modificar el analizador de números, como siempre analizaba . como punto decimal. Puede ser el primer carácter del operador de concatenación .. .
Contexto del compilador
Durante la compilación, las diferentes funciones del compilador necesitan obtener información sobre el código compilado hasta el momento. Mantendremos esa información en una clase compiler_context . Dado que estamos a punto de implementar el análisis de expresiones, necesitaremos recuperar información sobre los identificadores que encontramos.
Durante el tiempo de ejecución, mantendremos las variables en dos contenedores diferentes. Uno de ellos será el contenedor de variables globales y otro será la pila. La pila crecerá a medida que llamamos funciones e ingresamos ámbitos. Se reducirá a medida que regresemos de las funciones y dejemos los ámbitos. Cuando llamamos a alguna función, presionaremos los parámetros de la función y luego la función se ejecutará. Su valor de retorno será empujado a la parte superior de la pila cuando se vaya. Por lo tanto, para cada función, la pila se verá así:
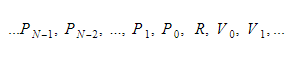
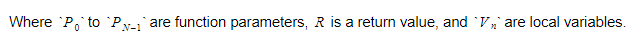
La función mantendrá el índice absoluto de la variable de retorno, y cada variable o parámetro se encontrará en relación con ese índice.
Por ahora, trataremos las funciones como identificadores globales constantes.
Esta es la clase que sirve como información de identificador:
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; Para variables locales y parámetros de función, el index función devuelve el índice relativo al valor de retorno. Devuelve el índice global absoluto en caso de identificadores globales.
Tendremos tres búsquedas de identificadores diferentes en compile_context :
- Búsqueda de identificador global, que
compile_contextel contexto por valor, ya que es el mismo en toda la compilación. - Búsqueda de identificador local, como
unique_ptr, que seránullptren el ámbito global y se inicializará en cualquier función. Cada vez que ingresemos al alcance, el nuevo contexto local se inicializará con el anterior como su padre. Cuando dejemos el alcance, será reemplazado por su padre. - Búsqueda de identificador de función, que será el puntero sin procesar. Será
nullptren ámbito global y el mismo valor que el ámbito local más externo en cualquier función.
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };Árbol de expresión
Cuando se analizan los tokens de expresión, se convierten en un árbol de expresión. Al igual que todos los árboles, este también consta de nodos.

Hay dos tipos diferentes de nodos:
- Nodos hoja, que pueden ser:
a) Identificadores
b) Números
c) Cuerdas - Nodos internos, que representan una operación en sus nodos secundarios. Mantiene a sus hijos con
unique_ptr.
Para cada nodo, hay información sobre su tipo y si devuelve o no un valor l (un valor que puede aparecer en el lado izquierdo del operador = ).
Cuando se crea un nodo interno, intentará convertir los tipos de retorno de sus hijos en los tipos que espera. Se permiten las siguientes conversiones implícitas:
- lvalue a no-lvalue
- Cualquier cosa para
void -
numberastring
Si no se permite la conversión, se arrojará un error semántico.
Aquí está la definición de clase, sin algunas funciones auxiliares y detalles de implementación:
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; La funcionalidad de los métodos se explica por sí misma, excepto por la función check_conversion . Verificará si el tipo es convertible al type_id pasado y al valor booleano lvalue obedeciendo las reglas de conversión de tipo y lanzará una excepción si no lo es.
Si un nodo se inicializa con std::string o double , su tipo será string o number , respectivamente, y no será un lvalue. Si se inicializa con un identificador, asumirá el tipo de ese identificador y será un valor l si el identificador no es constante.
Sin embargo, si se inicializa con una operación de nodo, su tipo dependerá de la operación y, a veces, del tipo de sus hijos. Escribamos los tipos de expresión en la tabla. Usaré & sufijo para denotar un lvalue. En los casos en que varias expresiones tengan el mismo tratamiento, escribiré expresiones adicionales entre corchetes.
Operaciones unarias
| Operación | Tipo de operación | tipo x |
| ++x (--x) | número& | número& |
| x++ (x--) | número | número& |
| +x (-x ~x !x) | número | número |
Operaciones Binarias
| Operación | Tipo de operación | tipo x | tipo |
| x+y (xy x*yx/yx\yx%y x&y x|yx^y x<<y x>>y x&&y x||y) | número | número | número |
| x==y (x!=y x<y x>y x<=y x>=y) | número | número o cadena | igual que x |
| x..y | cuerda | cuerda | cuerda |
| x=y | igual que x | valor de cualquier cosa | igual que x, sin lvalue |
| x+=y (x-=yx*=yx/=yx\=yx%=y x&=yx|=yx^=y x<<=y x>>=y) | número& | número& | número |
| x..=y | cuerda& | cuerda& | cuerda |
| x,y | igual que tu | vacío | cualquier cosa |
| x[y] | tipo de elemento de x | tipo de matriz | número |
Operaciones Ternarias
| Operación | Tipo de operación | tipo x | tipo | tipo z |
| x?y:z | igual que tu | número | cualquier cosa | igual que tu |
Llamada de función
Cuando se trata de la llamada de función, las cosas se complican un poco más. Si la función tiene N argumentos, la operación de llamada de función tiene N+1 hijos, donde el primer hijo es la propia función y el resto de los hijos corresponden a los argumentos de la función.
Sin embargo, no permitiremos pasar implícitamente argumentos por referencia. Requeriremos que la persona que llama los prefije con el signo & . Por ahora, ese no será un operador adicional, sino la forma en que se analiza la llamada a la función. Si no analizamos el ampersand, cuando se espera el argumento, eliminaremos el lvalue-ness de ese argumento agregando una operación unaria falsa que llamamos node_operation::param . Esa operación tiene el mismo tipo que su hijo, pero no es un lvalue.
Luego, cuando construimos el nodo con esa operación de llamada, si tenemos un argumento que es lvalue pero la función no lo espera, generaremos un error, ya que significa que la persona que llamó escribió el ampersand accidentalmente. Sorprendentemente, que & , si se trata como un operador, tendría la menor precedencia, ya que no tiene el significado semántico si se analiza dentro de la expresión. Podemos cambiarlo más tarde.
Analizador de expresiones
En una de sus afirmaciones sobre el potencial de los programadores, el famoso filósofo de la informática Edsger Dijkstra dijo una vez:
“Es prácticamente imposible enseñar buena programación a estudiantes que han tenido una exposición previa a BASIC. Como programadores potenciales, están mentalmente mutilados más allá de toda esperanza de regeneración”.
Entonces, para todos los que no han estado expuestos a BASIC, estén agradecidos, ya que escaparon de la "mutilación mental".
El resto de nosotros, programadores mutilados, recordemos los días en que codificábamos en BASIC. Había un operador \ , que se usaba para la división integral. En un lenguaje donde no tienes tipos separados para números enteros y de coma flotante, eso es bastante útil, así que agregué el mismo operador a Stork. También agregué el operador \= , que, como adivinaste, realizará una división integral y luego asignará.
Creo que tales operadores serían apreciados por los programadores de JavaScript, por ejemplo. No quiero ni imaginar lo que diría Dijkstra sobre ellos si viviera lo suficiente para ver la creciente popularidad de JS.
Hablando de eso, uno de los mayores problemas que tengo con JavaScript es la discrepancia de las siguientes expresiones:
-
"1" - “1”se evalúa como0 -
"1" * “1”se evalúa como1 -
"1" / “1”se evalúa como1 -
"1" + “1”se evalúa como“11”
El dúo de hip-hop croata "Tram 11", llamado así por un tranvía que conecta los distritos periféricos de Zagreb, tenía una canción que se traduce aproximadamente como: "Uno y uno no son dos, sino 11". Salió a finales de los 90, por lo que no era una referencia a JavaScript, pero ilustra bastante bien la discrepancia.
Para evitar esas discrepancias, prohibí la conversión implícita de cadena a número y agregué .. operador para la concatenación (y ..= para la concatenación con asignación). No recuerdo de dónde saqué la idea de ese operador. No es de BASIC o PHP, y no buscaré la frase "concatenación de Python" porque buscar en Google cualquier cosa sobre Python me da escalofríos. Tengo fobia a las serpientes, y combino eso con la "concatenación" - ¡no, gracias! Tal vez más tarde, con algún navegador arcaico basado en texto, sin arte ASCII.
Pero volvamos al tema de esta sección: nuestro analizador de expresiones. Usaremos una adaptación del “Algoritmo del patio de maniobras”.
Ese es el algoritmo que viene a la mente de cualquier programador promedio después de pensar en el problema durante 10 minutos más o menos. Puede usarse para evaluar una expresión infija o transformarla a la notación polaca inversa, lo cual no haremos.
La idea del algoritmo es leer operandos y operadores de izquierda a derecha. Cuando leemos un operando, lo empujamos a la pila de operandos. Cuando leemos un operador, no podemos evaluarlo inmediatamente, ya que no sabemos si el siguiente operador tendrá mejor precedencia que ese. Por lo tanto, lo empujamos a la pila de operadores.
Sin embargo, primero verificamos si el operador en la parte superior de la pila tiene mejor precedencia que el que acabamos de leer. En ese caso, evaluamos el operador desde la parte superior de la pila con operandos en la pila de operandos. Empujamos el resultado a la pila de operandos. Lo mantenemos hasta que leemos todo y luego evaluamos todos los operadores a la izquierda de la pila de operadores con los operandos en la pila de operandos, empujando los resultados hacia atrás en la pila de operandos hasta que nos quedemos sin operadores y con solo un operando, que es el resultado.
Cuando dos operadores tengan la misma precedencia, tomaremos el de la izquierda en caso de que esos operadores sean asociativos por la izquierda; de lo contrario, tomamos la correcta. Dos operadores de la misma precedencia no pueden tener diferente asociatividad.
El algoritmo original también trata los corchetes, pero en su lugar lo haremos recursivamente, ya que el algoritmo será más limpio de esa manera.
Edsger Dijkstra nombró al algoritmo "Plaza de maniobras" porque se asemeja a la operación de una estación de maniobras de ferrocarril.
Sin embargo, el algoritmo original del patio de maniobras casi no verifica errores, por lo que es muy posible que una expresión no válida se analice como correcta. Por lo tanto, agregué la variable booleana que verifica si esperamos un operador o un operando. Si esperamos operandos, también podemos analizar operadores de prefijos unarios. De esa forma, ninguna expresión no válida puede pasar desapercibida y la verificación de la sintaxis de la expresión está completa.
Terminando
Cuando comencé a programar esta parte de la serie, planeé escribir sobre el generador de expresiones. Quería construir una expresión que se pueda evaluar. Sin embargo, resultó ser demasiado complicado para una publicación de blog, así que decidí dividirlo por la mitad. En esta parte, concluimos el análisis de expresiones, y escribiré sobre la creación de objetos de expresión en el próximo artículo.
Si no recuerdo mal, hace unos 15 años, me tomó un fin de semana escribir la primera versión de mi primer idioma, lo que me hace preguntarme qué salió mal esta vez.
En un esfuerzo por negar que me estoy haciendo mayor y menos ingenioso, culparé a mi hijo de dos años por ser demasiado exigente en mi tiempo libre.
Como en la Parte 1, puede leer, descargar o incluso compilar el código de mi página de GitHub.
