Stork,第 2 部分:创建表达式解析器
已发表: 2022-03-11在我们系列的这一部分中,我们将介绍编写语言引擎脚本的一个更棘手的(至少在我看来)组件,它是每种编程语言的基本构建块:表达式解析器。
读者可能会问的一个问题——这是理所当然的——是:为什么我们不简单地使用一些已经可以使用的复杂工具或库?
为什么我们不使用 Lex、YACC、Bison、Boost Spirit,或者至少是正则表达式?
在我们的整个关系中,我的妻子注意到了我不能否认的一个特点:每当遇到困难的问题时,我都会列出一个清单。 如果您考虑一下,那是完全有道理的——我用数量来弥补我的回答中缺乏质量。
我现在会做同样的事情。
- 我想使用标准 C++。 在这种情况下,这将是 C++17。 我认为该语言本身就非常丰富,我正在努力克服将标准库以外的任何东西添加到混合中的冲动。
- 当我开发我的第一个脚本语言时,我没有使用任何复杂的工具。 我承受着压力并且时间紧迫,但我不知道如何使用 Lex、YACC 或类似的东西。 因此,我决定手动开发所有内容。
- 后来,我找到了一位经验丰富的编程语言开发人员的博客,他建议不要使用任何这些工具。 他说这些工具解决了语言开发中较容易的部分,所以无论如何,你都会遇到困难的事情。 我现在找不到那个博客,因为那是很久以前,当互联网和我都很年轻的时候。
- 同时,有一个表情包说: “你有一个问题,你决定使用正则表达式来解决。 现在你有两个问题。”
- 我不知道 Lex、YACC、Bison 或类似的东西。 我知道 Boost Spirit,它是一个方便且令人惊叹的库,但我仍然更喜欢更好地控制解析器。
- 我喜欢手动完成这些组件。 实际上,我可以给出这个答案并完全删除这个列表。
完整代码可在我的 GitHub 页面上找到。
令牌迭代器
第 1 部分中的代码有一些更改。
这些大多是简单的修复和小的更改,但现有解析代码的一个重要补充是类token_iterator 。 它允许我们评估当前令牌而不将其从流中删除,这非常方便。
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; 它使用push_back_stream初始化,然后可以取消引用和递增。 可以使用显式 bool 强制转换来检查它,当当前令牌等于 eof 时,它将评估为 false。
静态或动态类型语言?
在这一部分我必须做出一个决定:这种语言是静态类型的还是动态类型的?
静态类型语言是一种在编译时检查其变量类型的语言。
另一方面,动态类型语言不会在编译期间检查它(如果有编译,这对于动态类型语言不是必需的),而是在执行期间。 因此,潜在的错误可能会一直存在于代码中,直到它们被命中。
这是静态类型语言的一个明显优势。 每个人都喜欢尽快发现自己的错误。 我一直想知道动态类型语言的最大优势是什么,最近几周我得到了答案:它更容易开发!
我之前开发的语言是动态类型的。 我或多或少对结果感到满意,编写表达式解析器并不太难。 您基本上不必检查变量类型,并且您依赖于运行时错误,您几乎可以自发地编写代码。
例如,如果您必须编写二进制+运算符并且想要为数字执行此操作,则只需在运行时将该运算符的两边都计算为数字。 如果任何一方都无法评估该数字,则只需抛出异常即可。 我什至通过检查表达式中变量的运行时类型信息来实现运算符重载,并且运算符是该运行时信息的一部分。
在我开发的第一种语言(这是我的第三种语言)中,我在编译时进行了类型检查,但我没有充分利用这一点。 表达式评估仍然取决于运行时类型信息。
现在,我决定开发一种静态类型语言,结果证明这是一项比预期困难得多的任务。 但是,由于我不打算将其编译为二进制文件或任何类型的模拟汇编代码,因此某些类型的信息将隐含在编译后的代码中。
类型
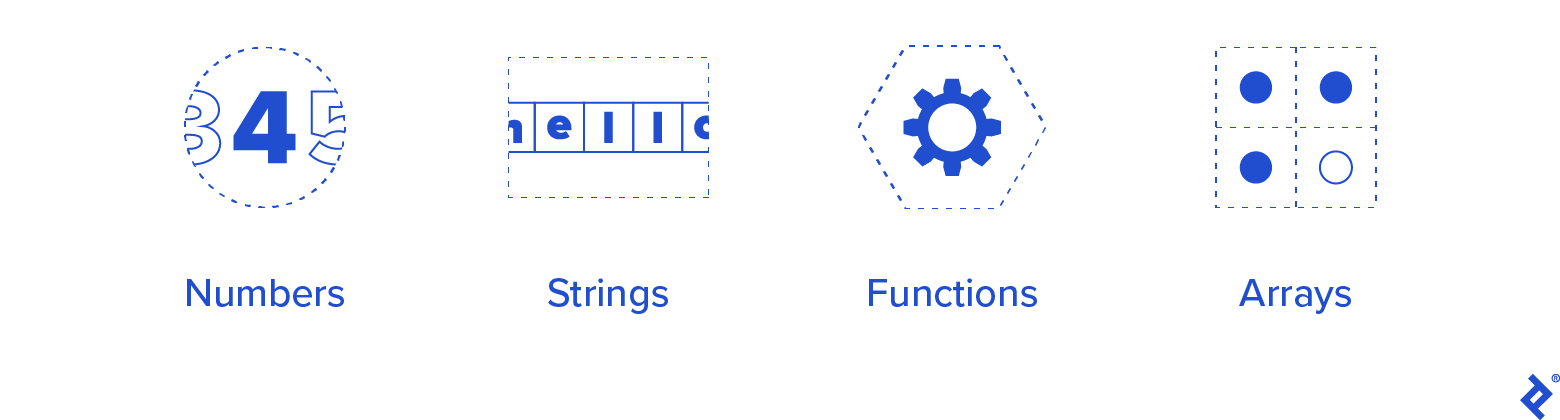
作为我们必须支持的最低限度的类型,我们将从以下内容开始:
- 数字
- 字符串
- 职能
- 数组
尽管我们可能会在未来添加它们,但我们不会在一开始就支持结构(或类、记录、元组等)。 但是,我们会记住,我们可能会在以后添加它们,所以我们不会用难以改变的决定来密封我们的命运。
首先,我想将类型定义为字符串,这将遵循一些约定。 每个标识符都会在编译时按值保留该字符串,有时我们必须对其进行解析。 例如,如果我们将数字数组的类型编码为“[number]”,那么我们必须修剪第一个和最后一个字符以获得内部类型,在本例中为“number”。 如果您考虑一下,这是一个非常糟糕的主意。
然后,我尝试将它作为一个类来实现。 该类将包含有关该类型的所有信息。 每个标识符都会保留一个指向该类的共享指针。 最后,我考虑在编译期间使用所有类型的注册表,因此每个标识符都有指向其类型的原始指针。
我喜欢这个主意,所以我们最终得到了以下结果:
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;简单类型是枚举的成员:
enum struct simple_type { nothing, number, string, }; 枚举成员nothing在这里作为void的占位符,我不能使用它,因为它是 C++ 中的关键字。
数组类型用具有type_handle唯一成员的结构表示。
struct array_type { type_handle inner_type_id; }; 显然,数组长度不是array_type的一部分,所以数组会动态增长。 这意味着我们最终会得到std::deque或类似的东西,但我们稍后会处理。
函数类型由其返回类型、每个参数的类型以及每个参数是通过值传递还是通过引用传递。
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };现在,我们可以定义将保留这些类型的类。
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; 类型保存在std::set中,因为该容器是稳定的,这意味着即使在插入新类型之后,指向其成员的指针也是有效的。 有函数get_handle ,它注册传递的类型并返回指向它的指针。 如果该类型已经注册,它将返回指向现有类型的指针。 还有一些方便的函数可以获取原始类型。
至于类型之间的隐式转换,数字将可以转换为字符串。 这不应该是危险的,因为不可能进行反向转换,并且字符串连接的运算符与数字加法的运算符不同。 即使在这种语言开发的后期阶段取消了这种转换,它也可以作为一个很好的练习。 为此,我不得不修改数字解析器,因为它总是解析. 作为小数点。 它可能是连接运算符的第一个字符..
编译器上下文
在编译过程中,不同的编译器函数需要获取到目前为止编译的代码的信息。 我们将把这些信息保存在类compiler_context中。 由于我们即将实现表达式解析,我们将需要检索有关我们遇到的标识符的信息。
在运行时,我们会将变量保存在两个不同的容器中。 其中一个是全局变量容器,另一个是堆栈。 当我们调用函数并进入作用域时,堆栈会增长。 当我们从函数返回并离开作用域时,它会缩小。 当我们调用某个函数时,我们会推送函数参数,然后函数就会执行。 当它离开时,它的返回值将被压入栈顶。 因此,对于每个函数,堆栈将如下所示:
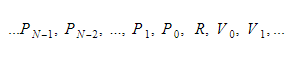
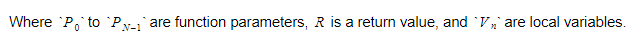
该函数将保留返回变量的绝对索引,并且每个变量或参数都将相对于该索引找到。
现在,我们将函数视为常量全局标识符。
这是用作标识符信息的类:
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; 对于局部变量和函数参数,函数index返回相对于返回值的索引。 如果是全局标识符,它会返回绝对全局索引。
我们将在compile_context中进行三种不同的标识符查找:
- 全局标识符查找,它将按值保存
compile_context,因为它在整个编译过程中都是相同的。 - 本地标识符查找,作为一个
unique_ptr,它将在全局范围内为nullptr并将在任何函数中初始化。 每当我们进入作用域时,新的本地上下文将被初始化为旧的作为其父上下文。 当我们离开作用域时,它会被它的父代取代。 - 函数标识符查找,它将是原始指针。 它将在全局范围内为
nullptr,并且与任何函数中最外层的本地范围具有相同的值。
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };表达式树
解析表达式标记时,它们将转换为表达式树。 与所有树类似,这棵树也由节点组成。

有两种不同类型的节点:
- 叶节点,可以是:
a) 标识符
b) 数字
c) 字符串 - 内部节点,表示对其子节点的操作。 它用
unique_ptr保留它的孩子。
对于每个节点,都有关于其类型以及它是否返回左值(可以出现在=运算符左侧的值)的信息。
创建内部节点时,它将尝试将其子节点的返回类型转换为它期望的类型。 允许以下隐式转换:
- 左值到非左值
- 什么都可以
void -
number到string
如果不允许转换,则会抛出语义错误。
这是类定义,没有一些辅助函数和实现细节:
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; 方法的功能是不言自明的,除了函数check_conversion 。 它将通过遵守类型转换规则检查类型是否可转换为传递的type_id和 boolean lvalue ,如果不是则抛出异常。
如果一个节点是用std::string或double初始化的,它的类型将分别是string或number ,而不是左值。 如果它是用标识符初始化的,它将假定该标识符的类型,如果标识符不是常量,它将是一个左值。
但是,如果使用节点操作对其进行初始化,则其类型将取决于操作,有时还取决于其子项的类型。 让我们在表中编写表达式类型。 我将使用&后缀来表示左值。 如果多个表达式具有相同的处理方式,我将在圆括号中写出额外的表达式。
一元运算
| 手术 | 操作类型 | x型 |
| ++x (--x) | 数字& | 数字& |
| x++ (x--) | 数字 | 数字& |
| +x (-x ~x !x) | 数字 | 数字 |
二元运算
| 手术 | 操作类型 | x型 | y型 |
| x+y (xy x*yx/yx\yx%y x&y x|yx^y x<<y x>>y x&&y x||y) | 数字 | 数字 | 数字 |
| x==y (x!=y x<y x>y x<=y x>=y) | 数字 | 数字或字符串 | 与 x 相同 |
| x..y | 细绳 | 细绳 | 细绳 |
| x=y | 与 x 相同 | 任何事物的左值 | 与 x 相同,没有左值 |
| x+=y (x-=yx*=yx/=yx\=yx%=y x&=yx|=yx^=y x<<=y x>>=y) | 数字& | 数字& | 数字 |
| x..=y | 细绳& | 细绳& | 细绳 |
| x,y | 和 y 一样 | 空白 | 任何事物 |
| x[y] | x的元素类型 | 数组类型 | 数字 |
三元运算
| 手术 | 操作类型 | x型 | y型 | z型 |
| x?y:z | 和 y 一样 | 数字 | 任何事物 | 和 y 一样 |
函数调用
当涉及到函数调用时,事情变得有点复杂。 如果函数有 N 个参数,则函数调用操作有 N+1 个子级,其中第一个子级是函数本身,其余子级对应于函数参数。
但是,我们不允许通过引用隐式传递参数。 我们将要求调用者在它们前面加上&符号。 目前,这不是一个额外的运算符,而是函数调用的解析方式。 如果我们不解析 & 符号,那么当需要参数时,我们将通过添加一个我们称为node_operation::param的假一元操作来从该参数中删除左值。 该操作与其子操作具有相同的类型,但它不是左值。
然后,当我们使用该调用操作构建节点时,如果我们有一个左值但函数不期望的参数,我们将产生错误,因为这意味着调用者不小心输入了 & 符号。 有点令人惊讶的是,如果将&视为运算符,则其优先级最低,因为如果在表达式内部进行解析,它在语义上没有意义。 我们稍后可能会更改它。
表达式解析器
著名的计算机科学哲学家 Edsger Dijkstra 在他关于程序员潜力的一项声明中曾经说过:
“向之前接触过 BASIC 的学生教授好的编程实际上是不可能的。 作为潜在的程序员,他们在精神上被残缺不全,没有再生的希望。”
所以,对于所有没有接触过 BASIC 的人 - 感激不尽,因为你逃脱了“精神伤害”。
我们这些残缺不全的程序员,让我们提醒自己使用 BASIC 编码的日子。 有一个运算符\ ,用于整数除法。 在你没有单独的整数和浮点数类型的语言中,这非常方便,所以我在 Stork 中添加了相同的运算符。 我还添加了运算符\= ,正如您所猜测的那样,它将执行整数除法然后分配。
例如,我认为 JavaScript 程序员会喜欢这样的运算符。 我什至不想想象如果 Dijkstra 活得足够长,看到 JS 越来越受欢迎,他会对他们说些什么。
说到这,我在 JavaScript 中遇到的最大问题之一是以下表达式的差异:
-
"1" - “1”计算为0 -
"1" * “1”计算结果为1 -
"1" / “1”计算为1 -
"1" + “1”计算为“11”
克罗地亚嘻哈二人组“Tram 11”以连接萨格勒布外围行政区的电车命名,有一首歌大致翻译为: “一加一不是二,而是 11”。 它出现在 90 年代后期,因此它不是对 JavaScript 的引用,但它很好地说明了这种差异。
为了避免这些差异,我禁止从字符串到数字的隐式转换,并添加了..运算符用于连接(以及..=用于与赋值的连接)。 我不记得我从哪里得到那个操作员的想法。 它不是来自 BASIC 或 PHP,我不会搜索短语“Python concatenation”,因为在谷歌上搜索任何关于 Python 的内容都会让我脊背发凉。 我对蛇有恐惧症,并将其与“串联”结合起来——不,谢谢! 也许稍后,使用一些古老的基于文本的浏览器,没有 ASCII 艺术。
但回到本节的主题——我们的表达式解析器。 我们将使用“调车场算法”的改编版。
这是任何一个普通程序员在考虑这个问题 10 分钟左右后都会想到的算法。 它可用于计算中缀表达式或将其转换为反向波兰表示法,我们不会这样做。
该算法的思想是从左到右读取操作数和运算符。 当我们读取一个操作数时,我们将它压入操作数堆栈。 当我们读取一个运算符时,我们不能立即评估它,因为我们不知道后面的运算符是否会比那个有更好的优先级。 因此,我们将其推送到操作员堆栈。
但是,我们首先检查堆栈顶部的运算符是否比我们刚刚读取的运算符具有更好的优先级。 在这种情况下,我们使用操作数堆栈上的操作数从堆栈顶部评估运算符。 我们将结果推送到操作数堆栈。 我们一直保留它,直到我们读取所有内容,然后使用操作数堆栈上的操作数评估操作数堆栈左侧的所有运算符,将结果推回操作数堆栈,直到我们没有运算符且只有一个操作数,即结果。
当两个运算符具有相同的优先级时,我们将取左一个,以防这些运算符是左结合的; 否则,我们选择正确的。 相同优先级的两个运算符不能具有不同的关联性。
原始算法也处理圆括号,但我们将改为递归处理,因为这样算法会更干净。
Edsger Dijkstra 将该算法命名为“调车场”,因为它类似于铁路调车场的操作。
然而,原来的调车场算法几乎不做错误检查,所以很有可能一个无效的表达式被解析为一个正确的表达式。 因此,我添加了布尔变量来检查我们是否需要一个运算符或一个操作数。 如果我们期望操作数,我们也可以解析一元前缀运算符。 这样一来,任何无效表达式都不会被忽视,表达式语法检查就完成了。
包起来
当我开始编写本系列的这一部分时,我计划写关于表达式构建器的文章。 我想构建一个可以评估的表达式。 然而,对于一篇博客文章来说,它太复杂了,所以我决定把它分成两半。 在这一部分,我们总结了解析表达式,我将在下一篇文章中写关于构建表达式对象的内容。
如果我没记错的话,大约 15 年前,我花了一个周末来写我的第一语言的第一个版本,这让我想知道这次出了什么问题。
为了否认自己年纪大了,不那么机智了,我会责怪我两岁的儿子在业余时间要求太高。
与第 1 部分一样,欢迎您从我的 GitHub 页面阅读、下载甚至编译代码。
