Bocian, część 2: Tworzenie analizatora wyrażeń
Opublikowany: 2022-03-11W tej części naszej serii omówimy jeden z trudniejszych (przynajmniej moim zdaniem) elementów skryptu silnika językowego, który jest niezbędnym elementem budulcowym każdego języka programowania: parser wyrażeń.
Pytanie, które czytelnik mógłby zadać — i słusznie — brzmi: Dlaczego po prostu nie skorzystamy z jakichś wyrafinowanych narzędzi lub bibliotek, które są już do naszej dyspozycji?
Dlaczego nie użyjemy Lex, YACC, Bison, Boost Spirit lub przynajmniej wyrażeń regularnych?
Przez cały nasz związek moja żona zauważyła moją cechę, której nie mogę zaprzeczyć: zawsze, gdy mam do czynienia z trudnym pytaniem, robię listę. Jeśli się nad tym zastanowić, to ma sens — używam ilości, aby zrekompensować brak jakości w mojej odpowiedzi.
Teraz zrobię to samo.
- Chcę użyć standardowego C++. W tym przypadku będzie to C++17. Myślę, że sam język jest dość bogaty i walczę z chęcią dodania czegokolwiek poza standardową biblioteką do miksu.
- Kiedy opracowałem swój pierwszy język skryptowy, nie używałem żadnych wyrafinowanych narzędzi. Byłem pod presją i miałem napięty termin, ale nie wiedziałem, jak korzystać z Lexa, YACC ani niczego podobnego. Dlatego postanowiłem wszystko rozwijać ręcznie.
- Później trafiłem na blog doświadczonego programisty języka programowania, który odradzał korzystanie z któregokolwiek z tych narzędzi. Powiedział, że te narzędzia rozwiązują łatwiejszą część rozwoju języka, więc w każdym razie pozostajesz z trudnymi rzeczami. Nie mogę teraz znaleźć tego bloga, tak jak to było dawno temu, kiedy zarówno internet, jak i ja byliśmy młodzi.
- W tym samym czasie pojawił się mem, który mówił: „Masz problem, który postanawiasz rozwiązać za pomocą wyrażeń regularnych. Teraz masz dwa problemy.”
- Nie znam Lexa, YACCa, Bisona ani niczego podobnego. Znam Boost Spirita i jest to poręczna i niesamowita biblioteka, ale nadal wolę mieć lepszą kontrolę nad parserem.
- Lubię robić te elementy ręcznie. Właściwie mógłbym po prostu udzielić tej odpowiedzi i całkowicie usunąć tę listę.
Pełny kod jest dostępny na mojej stronie GitHub.
Iterator tokenów
Jest kilka zmian w kodzie z Części 1.
Są to w większości proste poprawki i drobne zmiany, ale ważnym dodatkiem do istniejącego kodu parsującego jest klasa token_iterator . Pozwala nam ocenić bieżący token bez usuwania go ze strumienia, co jest bardzo przydatne.
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; Jest inicjowany za pomocą push_back_stream , a następnie można go wyłuskać i zwiększyć. Można to sprawdzić za pomocą jawnego rzutowania logicznego, które zostanie ocenione jako false, gdy bieżący token jest równy eof.
Język wpisywany statycznie czy dynamicznie?
W tej części muszę podjąć jedną decyzję: czy ten język będzie pisany statycznie czy dynamicznie?
Język statycznie typowany to język, który sprawdza typy swoich zmiennych w czasie kompilacji.
Z drugiej strony język z typowaniem dynamicznym nie sprawdza tego podczas kompilacji (jeśli istnieje kompilacja, która nie jest obowiązkowa dla języka z typowaniem dynamicznym), ale podczas wykonywania. Dlatego potencjalne błędy mogą żyć w kodzie, dopóki nie zostaną trafione.
Jest to oczywista zaleta języków statycznie typowanych. Każdy lubi jak najszybciej wyłapać swoje błędy. Zawsze zastanawiałem się, jaka jest największa zaleta języków dynamicznie typowanych, a odpowiedź uderzyła mnie w ciągu ostatnich kilku tygodni: Dużo łatwiej się rozwija!
Poprzedni język, który opracowałem, był pisany dynamicznie. Byłem mniej lub bardziej zadowolony z wyniku, a napisanie parsera wyrażeń nie było zbyt trudne. Zasadniczo nie musisz sprawdzać typów zmiennych i polegasz na błędach uruchomieniowych, które kodujesz niemal spontanicznie.
Na przykład, jeśli musisz napisać operator binarny + i chcesz to zrobić dla liczb, wystarczy obliczyć obie strony tego operatora jako liczby w czasie wykonywania. Jeśli którakolwiek ze stron nie może ocenić liczby, po prostu rzucasz wyjątek. Zaimplementowałem nawet przeciążanie operatorów, sprawdzając informacje o typie środowiska wykonawczego zmiennych w wyrażeniu, a operatory były częścią tych informacji o środowisku wykonawczym.
W pierwszym opracowanym przeze mnie języku (jest to mój trzeci) sprawdzałem typ w czasie kompilacji, ale nie wykorzystałem tego w pełni. Ocena wyrażenia nadal była zależna od informacji o typie środowiska uruchomieniowego.
Teraz postanowiłem stworzyć język statycznie typowany i okazało się to znacznie trudniejszym zadaniem niż się spodziewałem. Jednakże, ponieważ nie planuję kompilować go do pliku binarnego lub jakiegokolwiek rodzaju emulowanego kodu asemblera, pewien rodzaj informacji będzie niejawnie istniał w skompilowanym kodzie.
Rodzaje
Jako minimum typów, które musimy obsługiwać, zaczniemy od następujących:
- Liczby
- Smyczki
- Funkcje
- Tablice
Chociaż możemy je dodawać w przyszłości, na początku nie będziemy obsługiwać struktur (lub klas, rekordów, krotek itp.). Pamiętajmy jednak, że możemy je później dodać, aby nie przypieczętować naszego losu trudnymi do zmiany decyzjami.
Najpierw chciałem zdefiniować typ jako ciąg znaków, zgodnie z pewną konwencją. Każdy identyfikator zachowałby ten ciąg według wartości w czasie kompilacji i czasami będziemy musieli go przeanalizować. Na przykład, jeśli zakodujemy typ tablicy liczb jako „[liczba]”, będziemy musieli przyciąć pierwszy i ostatni znak, aby uzyskać typ wewnętrzny, którym w tym przypadku jest „liczba”. To całkiem zły pomysł, jeśli się nad tym zastanowić.
Następnie spróbowałem zaimplementować to jako klasę. Ta klasa miałaby wszystkie informacje o typie. Każdy identyfikator utrzymywałby wspólny wskaźnik do tej klasy. W końcu pomyślałem o posiadaniu rejestru wszystkich typów użytych podczas kompilacji, aby każdy identyfikator miał surowy wskaźnik do swojego typu.
Podobał mi się ten pomysł, więc otrzymaliśmy następujące:
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;Typy proste są członkami wyliczenia:
enum struct simple_type { nothing, number, string, }; Element członkowski wyliczenia nothing jest tutaj miejscem zastępczym dla void , którego nie mogę użyć, ponieważ jest to słowo kluczowe w C++.
Typy tablic są reprezentowane przez strukturę, która ma jedyny element członkowski type_handle .
struct array_type { type_handle inner_type_id; }; Oczywiście długość tablicy nie jest częścią array_type , więc tablice będą rosły dynamicznie. Oznacza to, że otrzymamy std::deque lub coś podobnego, ale zajmiemy się tym później.
Typ funkcji składa się z typu zwracanego, typu każdego z jej parametrów oraz tego, czy każdy z tych parametrów jest przekazywany przez wartość, czy przez odwołanie.
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };Teraz możemy zdefiniować klasę, która zachowa te typy.
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; Typy są przechowywane w std::set , ponieważ kontener jest stabilny, co oznacza, że wskaźniki do jego elementów członkowskich są prawidłowe nawet po wstawieniu nowych typów. Istnieje funkcja get_handle , która rejestruje przekazany typ i zwraca do niego wskaźnik. Jeśli typ jest już zarejestrowany, zwróci wskaźnik do istniejącego typu. Istnieją również funkcje ułatwiające pobieranie typów pierwotnych.
Jeśli chodzi o niejawną konwersję między typami, liczby będą konwertowane na łańcuchy. Nie powinno to być niebezpieczne, ponieważ odwrotna konwersja nie jest możliwa, a operator konkatenacji łańcuchów różni się od operatora dodawania liczb. Nawet jeśli ta konwersja zostanie usunięta na późniejszych etapach rozwoju tego języka, będzie dobrze służyć jako ćwiczenie w tym momencie. W tym celu musiałem zmodyfikować parser liczb, ponieważ zawsze parsował . jako przecinek dziesiętny. Może to być pierwszy znak operatora konkatenacji .. .
Kontekst kompilatora
Podczas kompilacji różne funkcje kompilatora muszą uzyskać informacje o dotychczas skompilowanym kodzie. Będziemy przechowywać te informacje w klasie compiler_context . Ponieważ mamy zamiar zaimplementować analizę składniową wyrażeń, będziemy musieli pobrać informacje o napotkanych identyfikatorach.
W czasie wykonywania będziemy przechowywać zmienne w dwóch różnych kontenerach. Jedną z nich będzie kontener zmiennej globalnej, a drugą stos. Stos będzie rósł, gdy będziemy wywoływać funkcje i wprowadzać zakresy. Zmniejszy się, gdy wrócimy z funkcji i opuścimy zakresy. Kiedy wywołujemy jakąś funkcję, wstawiamy parametry funkcji, a następnie funkcja zostanie wykonana. Jego wartość zwracana zostanie przesunięta na szczyt stosu, gdy opuści. Dlatego dla każdej funkcji stos będzie wyglądał tak:
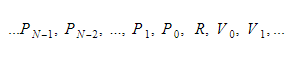
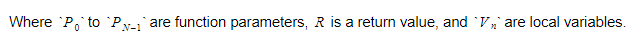
Funkcja zachowa indeks bezwzględny zwracanej zmiennej, a każda zmienna lub parametr zostanie znaleziona względem tego indeksu.
Na razie funkcje będziemy traktować jako stałe identyfikatory globalne.
To jest klasa, która służy jako informacja o identyfikatorze:
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; W przypadku zmiennych lokalnych i parametrów funkcji index funkcji zwraca indeks względem wartości zwracanej. Zwraca bezwzględny indeks globalny w przypadku identyfikatorów globalnych.
Będziemy mieli trzy różne wyszukiwania identyfikatorów w compile_context :
- Wyszukiwanie globalnego identyfikatora, który
compile_contextbędzie przechowywany według wartości, ponieważ jest taki sam w całej kompilacji. - Lokalne wyszukiwanie identyfikatora, jako
unique_ptr, które będzienullptrw zakresie globalnym i zostanie zainicjowane w dowolnej funkcji. Za każdym razem, gdy wejdziemy w zakres, nowy kontekst lokalny zostanie zainicjowany ze starym jako jego rodzicem. Gdy opuścimy zakres, zastąpi go jego rodzic. - Wyszukiwanie identyfikatora funkcji, który będzie surowym wskaźnikiem. Będzie to
nullptrw zasięgu globalnym i taka sama wartość jak najbardziej zewnętrzny zasięg lokalny w dowolnej funkcji.
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };Drzewo wyrażeń
Podczas analizowania tokenów wyrażeń są one konwertowane na drzewo wyrażeń. Podobnie jak wszystkie drzewa, to również składa się z węzłów.

Istnieją dwa różne rodzaje węzłów:
- Węzły liściowe, którymi mogą być:
a) Identyfikatory
b) Liczby
c) Struny - Węzły wewnętrzne, które reprezentują operację na ich węzłach podrzędnych. Zachowuje swoje dzieci z
unique_ptr.
Dla każdego węzła dostępne są informacje o jego typie oraz o tym, czy zwraca on l-wartość (wartość, która może pojawić się po lewej stronie operatora = ).
Kiedy tworzony jest węzeł wewnętrzny, spróbuje przekonwertować zwracane typy swoich dzieci na typy, których oczekuje. Dozwolone są następujące konwersje niejawne:
- lwartość na inną niż lwartość
- Wszystko do
void -
numberdostring
Jeśli konwersja nie jest dozwolona, zostanie zgłoszony błąd semantyczny.
Oto definicja klasy, bez niektórych funkcji pomocniczych i szczegółów implementacji:
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; Funkcjonalność metod jest oczywista, z wyjątkiem funkcji check_conversion . Sprawdza, czy typ jest konwertowalny na przekazany type_id i boolean lvalue , przestrzegając reguł konwersji typu i zgłosi wyjątek, jeśli tak nie jest.
Jeśli węzeł jest inicjowany za pomocą std::string lub double , jego typem będzie odpowiednio string lub number , a nie będzie lwartością. Jeśli jest zainicjowany identyfikatorem, przyjmie typ tego identyfikatora i będzie lwartością, jeśli identyfikator nie jest stały.
Jeśli jednak zostanie zainicjowany za pomocą operacji węzła, jego typ będzie zależał od operacji, a czasami od typu jej elementów potomnych. Zapiszmy typy wyrażeń w tabeli. Użyję & sufiksu do oznaczenia l-wartości. W przypadku, gdy wiele wyrażeń jest traktowanych tak samo, dopiszę dodatkowe wyrażenia w nawiasach okrągłych.
Operacje jednoargumentowe
| Operacja | Rodzaj operacji | x typ |
| ++x (--x) | numer& | numer& |
| x++ (x--) | numer | numer& |
| +x (-x ~x !x) | numer | numer |
Operacje binarne
| Operacja | Rodzaj operacji | x typ | y typ |
| x+y (xy x*yx/yx\yx%y x&y x|yx^y x<<y x>>y x&&y x||y) | numer | numer | numer |
| x==y (x!=y x<y x>y x<=y x>=y) | numer | liczba lub ciąg | to samo co x |
| x..y | strunowy | strunowy | strunowy |
| x=y | to samo co x | wartość czegokolwiek | to samo co x, bez lwartości |
| x+=y (x-=yx*=yx/=yx\=yx%=y x&=yx|=yx^=y x<<=y x>>=y) | numer& | numer& | numer |
| x..=y | strunowy& | strunowy& | strunowy |
| x,y | tak samo jak ty | próżnia | wszystko |
| x[y] | typ elementu x | typ tablicy | numer |
Operacje trójskładnikowe
| Operacja | Rodzaj operacji | x typ | y typ | typ z |
| x?y:z? | tak samo jak ty | numer | wszystko | tak samo jak ty |
Wywołanie funkcji
Jeśli chodzi o wywołanie funkcji, sprawy trochę się komplikują. Jeśli funkcja ma N argumentów, operacja wywołania funkcji ma N+1 dzieci, gdzie pierwszym dzieckiem jest sama funkcja, a reszta dzieci odpowiada argumentom funkcji.
Nie pozwolimy jednak na niejawne przekazywanie argumentów przez odwołanie. Wymagamy, aby dzwoniący poprzedził go znakiem & . Na razie nie będzie to dodatkowy operator, ale sposób parsowania wywołania funkcji. Jeśli nie przeanalizujemy znaku &, gdy argument jest oczekiwany, usuniemy z tego argumentu lvalue-ness, dodając fałszywą jednoargumentową operację, którą nazywamy node_operation::param . Ta operacja ma ten sam typ co jej dziecko, ale nie jest lwartością.
Następnie, gdy budujemy węzeł z tą operacją wywołania, jeśli mamy argument będący lwartością, ale nie jest oczekiwany przez funkcję, wygenerujemy błąd, ponieważ oznacza to, że osoba wywołująca przypadkowo wpisała znak &. Nieco zaskakujące, że & , gdyby był traktowany jako operator, miałby najmniejszy priorytet, ponieważ nie ma znaczenia semantycznego, jeśli jest analizowany w wyrażeniu. Możemy to zmienić później.
Analizator wyrażeń
W jednym ze swoich twierdzeń o potencjale programistów, słynny filozof informatyki Edsger Dijkstra powiedział:
„Praktycznie niemożliwe jest nauczenie dobrego programowania uczniów, którzy mieli wcześniej kontakt z językiem BASIC. Jako potencjalni programiści są psychicznie okaleczeni bez nadziei na regenerację”.
Tak więc, dla wszystkich z was, którzy nie byli narażeni na BASIC – bądźcie wdzięczni, ponieważ uniknęliście „mentalnego okaleczenia”.
Reszta z nas, okaleczeni programiści, przypomnijmy sobie czasy, kiedy kodowaliśmy w BASIC-u. Istniał operator \ , który służył do dzielenia całkowego. W języku, w którym nie ma oddzielnych typów liczb całkowitych i zmiennoprzecinkowych, jest to całkiem przydatne, więc dodałem ten sam operator do Stork. Dodałem również operator \= , który, jak się domyślacie, dokona dzielenia całkowego, a następnie przypisze.
Myślę, że takie operatory doceniliby np. programiści JavaScript. Nie chcę sobie nawet wyobrażać, co powiedziałby o nich Dijkstra, gdyby żył wystarczająco długo, by zobaczyć rosnącą popularność JS.
Skoro o tym mowa, jednym z największych problemów, jakie mam z JavaScriptem, jest rozbieżność następujących wyrażeń:
-
"1" - “1”daje0 -
"1" * “1”daje1 -
"1" / “1”daje1 -
"1" + “1”daje“11”
Chorwacki duet hip-hopowy „Tram 11”, nazwany na cześć tramwaju łączącego odległe dzielnice Zagrzebia, miał piosenkę, którą można z grubsza przetłumaczyć jako: „Jeden i jeden to nie dwa, ale 11.”. Wyszedł pod koniec lat 90., więc nie był odniesieniem do JavaScriptu, ale całkiem dobrze ilustruje rozbieżność.
Aby uniknąć tych rozbieżności, zabroniłem niejawnej konwersji z łańcucha na liczbę i dodałem operator .. dla konkatenacji (oraz ..= dla łączenia z przypisaniem). Nie pamiętam skąd wpadł mi na pomysł tego operatora. Nie pochodzi z BASICa ani PHP i nie będę szukał frazy „konkatenacja Pythona”, ponieważ googlowanie czegokolwiek na temat Pythona przyprawia mnie o dreszcze. Mam fobię przed wężami, a łączenie tego z „konkatenacją” – nie, dzięki! Może później, z jakąś archaiczną przeglądarką tekstową, bez grafiki ASCII.
Wróćmy jednak do tematu tej sekcji - naszego parsera wyrażeń. Wykorzystamy adaptację „Algorytmu rozrządowego”.
Jest to algorytm, który przychodzi do głowy każdemu nawet przeciętnemu programiście po zastanowieniu się nad problemem przez około 10 minut. Można go użyć do oceny wyrażenia wrostkowego lub przekształcenia go na odwrotną notację polską, czego nie zrobimy.
Ideą algorytmu jest odczytywanie operandów i operatorów od lewej do prawej. Kiedy czytamy operand, odkładamy go na stos operandów. Kiedy czytamy operator, nie możemy go od razu ocenić, ponieważ nie wiemy, czy następny operator będzie miał wyższy priorytet niż ten. Dlatego wpychamy go na stos operatora.
Jednak najpierw sprawdzamy, czy operator na szczycie stosu ma wyższy priorytet niż ten, który właśnie przeczytaliśmy. W takim przypadku oceniamy operator ze szczytu stosu z operandami na stosie operandów. Wynik odkładamy na stos argumentów. Przechowujemy to, dopóki nie przeczytamy wszystkiego, a następnie ocenimy wszystkie operatory po lewej stronie stosu operatorów z operandami na stosie operandów, odkładając wyniki z powrotem na stos operandów, dopóki nie zostaniemy bez operatorów i tylko z jednym operandem, czyli wynik.
Gdy dwa operatory mają ten sam priorytet, weźmiemy lewy w przypadku, gdy te operatory są lewostronnie zespolone; w przeciwnym razie wybieramy właściwy. Dwa operatory o tym samym priorytecie nie mogą mieć różnej łączności.
Oryginalny algorytm traktuje również nawiasy okrągłe, ale zamiast tego zrobimy to rekurencyjnie, ponieważ w ten sposób algorytm będzie czystszy.
Edsger Dijkstra nazwał algorytm „Bocznicą rozrządową”, ponieważ przypomina on działanie stacji rozrządowej dla kolei.
Jednak oryginalny algorytm stacji rozrządowej prawie nie sprawdza błędów, więc jest całkiem możliwe, że nieprawidłowe wyrażenie zostanie przeanalizowane jako poprawne. Dlatego dodałem zmienną logiczną, która sprawdza, czy oczekujemy operatora czy operandu. Jeśli oczekujemy operandów, możemy również analizować jednoargumentowe operatory przedrostkowe. W ten sposób żadne nieprawidłowe wyrażenie nie może przejść pod radarem, a sprawdzanie składni wyrażenia jest zakończone.
Zawijanie
Kiedy zacząłem kodować do tej części serii, planowałem napisać o kreatorze ekspresji. Chciałem zbudować wyrażenie, które można ocenić. Okazało się to jednak zbyt skomplikowane na jeden wpis na blogu, więc postanowiłem podzielić go na pół. W tej części zakończyliśmy parsowanie wyrażeń, ao budowaniu obiektów wyrażeniowych napiszę w następnym artykule.
Jeśli dobrze pamiętam, jakieś 15 lat temu napisanie pierwszej wersji mojego pierwszego języka zajęło mi jeden weekend, co sprawia, że zastanawiam się, co tym razem poszło nie tak.
Próbując zaprzeczyć, że się starzeję i jestem mniej dowcipny, będę winić mojego dwuletniego syna za to, że jest zbyt wymagający w wolnym czasie.
Podobnie jak w części 1, możesz przeczytać, pobrać, a nawet skompilować kod z mojej strony GitHub.
