コウノトリ、パート2:式パーサーの作成
公開: 2022-03-11シリーズのこのパートでは、言語エンジンのスクリプト作成のトリッキーな(少なくとも私の意見では)コンポーネントの1つを取り上げます。これは、すべてのプログラミング言語にとって不可欠な構成要素である式パーサーです。
読者が尋ねることができる質問、そして当然のことながら、次のような質問があります。すでに自由に使える洗練されたツールやライブラリを単純に使用しないのはなぜですか。
Lex、YACC、Bison、Boost Spirit、または少なくとも正規表現を使用してみませんか?
私たちの関係を通して、私の妻は私が否定できない私の特徴に気づきました:難しい質問に直面するときはいつでも、私はリストを作ります。 あなたがそれについて考えるならば、それは完全に理にかなっています—私は私の答えの質の欠如を補うために量を使用しています。
今から同じことをします。
- 標準のC++を使用したい。 この場合、それはC++17になります。 言語自体は非常に豊富だと思います。私は、標準ライブラリ以外のものをミックスに追加したいという衝動と戦っています。
- 最初のスクリプト言語を開発したとき、洗練されたツールは使用していませんでした。 私はプレッシャーにさらされ、締め切りが厳しかったのですが、LexやYACCなどの使い方がわかりませんでした。 したがって、私はすべてを手動で開発することにしました。
- 後で、経験豊富なプログラミング言語開発者によるブログを見つけました。彼は、これらのツールのいずれも使用しないようにアドバイスしました。 彼は、これらのツールは言語開発のより簡単な部分を解決するので、いずれにせよ、あなたは難しいものを残されていると言いました。 インターネットも私も若い頃だったので、今はそのブログを見つけることができません。
- 同時に、 「正規表現を使って解決しようと決心した問題があります。 今、2つの問題があります。」
- Lex、YACC、Bisonなどは知りません。 私はBoostSpiritを知っており、それは便利で素晴らしいライブラリですが、それでもパーサーをより適切に制御することを好みます。
- 私はそれらのコンポーネントを手動で行うのが好きです。 実際、私はこの答えを出して、このリストを完全に削除することができました。
完全なコードは私のGitHubページで入手できます。
トークンイテレーター
パート1からコードにいくつかの変更があります。
これらは主に単純な修正と小さな変更ですが、既存の解析コードへの重要な追加の1つは、 token_iteratorクラスです。 これにより、ストリームから削除せずに現在のトークンを評価できます。これは非常に便利です。
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; これはpush_back_streamで初期化され、その後、逆参照およびインクリメントできます。 明示的なブールキャストでチェックできます。これは、現在のトークンがeofに等しい場合にfalseと評価されます。
静的または動的に型付けされた言語?
この部分で私がしなければならない決定が1つあります。この言語は静的または動的に型付けされますか?
静的に型付けされた言語は、コンパイル時にその変数の型をチェックする言語です。
一方、動的型付け言語は、コンパイル中(動的型付け言語では必須ではないコンパイルがある場合)ではなく、実行中にチェックします。 したがって、潜在的なエラーは、ヒットするまでコード内に存在する可能性があります。
これは、静的に型付けされた言語の明らかな利点です。 誰もができるだけ早くエラーをキャッチするのが好きです。 動的型付け言語の最大の利点は何であるかを常に疑問に思っていましたが、ここ数週間で答えがわかりました。開発がはるかに簡単です。
私が開発した以前の言語は動的に型付けされていました。 結果には多かれ少なかれ満足しており、式パーサーの記述はそれほど難しくありませんでした。 基本的に変数タイプをチェックする必要はなく、ほぼ自発的にコーディングするランタイムエラーに依存します。
たとえば、二項+演算子を作成する必要があり、数値に対してそれを実行する場合は、実行時にその演算子の両側を数値として評価する必要があります。 どちらかの側が数を評価できない場合は、例外をスローするだけです。 式内の変数の実行時型情報をチェックすることで演算子のオーバーロードを実装しましたが、演算子はその実行時情報の一部でした。
私が開発した最初の言語(これは私の3番目の言語です)では、コンパイル時に型チェックを行いましたが、それを十分に活用していませんでした。 式の評価は、実行時型情報に依存していました。
今、私は静的に型付けされた言語を開発することに決めました、そしてそれは予想よりはるかに難しい仕事であることがわかりました。 ただし、バイナリやエミュレートされたアセンブリコードにコンパイルする予定はないため、コンパイルされたコードにはある種の情報が暗黙的に存在します。
タイプ
サポートする必要のある最低限のタイプとして、以下から始めます。
- 数字
- 文字列
- 関数
- 配列
今後追加する可能性はありますが、最初は構造(またはクラス、レコード、タプルなど)をサポートしません。 ただし、後で追加する可能性があることを念頭に置いておくため、変更が難しい決定で運命を封じることはありません。
まず、型を文字列として定義したかったのですが、これはいくつかの規則に従います。 すべての識別子は、コンパイル時にその文字列を値ごとに保持するため、時々解析する必要があります。 たとえば、数値の配列の型を「[number]」としてエンコードする場合、内部型(この場合は「number」)を取得するために、最初と最後の文字をトリミングする必要があります。 あなたがそれについて考えるならば、それはかなり悪い考えです。
次に、それをクラスとして実装しようとしました。 そのクラスには、タイプに関するすべての情報が含まれます。 各識別子は、そのクラスへの共有ポインタを保持します。 結局、コンパイル中にすべてのタイプのレジストリを使用することを考えたので、各識別子にはそのタイプへの生のポインタがあります。
私はそのアイデアが好きだったので、次のようになりました。
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;単純型は列挙型のメンバーです:
enum struct simple_type { nothing, number, string, }; 列挙型メンバーは、 voidのプレースホルダーとしてここにはありnothingん。これは、C++のキーワードであるため使用できません。
配列型は、 type_handleの唯一のメンバーを持つ構造体で表されます。
struct array_type { type_handle inner_type_id; }; 明らかに、配列の長さはarray_typeの一部ではないため、配列は動的に大きくなります。 つまり、最終的にstd::dequeなどになりますが、後で処理します。
関数型は、戻り型、各パラメーターの型、およびこれらの各パラメーターが値または参照によって渡されるかどうかで構成されます。
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };これで、これらの型を保持するクラスを定義できます。
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; コンテナは安定しているため、型はstd::setに保持されます。つまり、新しい型が挿入された後でも、そのメンバーへのポインタは有効です。 渡された型を登録し、その型へのポインタを返す関数get_handleがあります。 タイプがすでに登録されている場合は、既存のタイプへのポインタを返します。 プリミティブ型を取得するための便利な関数もあります。
タイプ間の暗黙的な変換に関しては、数値は文字列に変換可能になります。 逆変換は不可能であり、文字列連結の演算子は数値加算の演算子とは異なるため、危険ではありません。 この言語の開発の後の段階でその変換が削除されたとしても、この時点での演習として役立ちます。 そのために、常に解析されるため、数値パーサーを変更する必要がありました. 小数点として。 連結演算子の最初の文字である可能性があり..
コンパイラコンテキスト
コンパイル中に、さまざまなコンパイラ関数が、これまでにコンパイルされたコードに関する情報を取得する必要があります。 その情報をクラスcompiler_contextに保持します。 式の解析を実装しようとしているので、遭遇した識別子に関する情報を取得する必要があります。
実行時に、変数を2つの異なるコンテナーに保持します。 それらの1つはグローバル変数コンテナーになり、もう1つはスタックになります。 関数を呼び出してスコープを入力すると、スタックが大きくなります。 関数から戻ってスコープを離れると、縮小します。 関数を呼び出すときは、関数パラメーターをプッシュしてから、関数を実行します。 その戻り値は、スタックを離れるときにスタックの一番上にプッシュされます。 したがって、各関数のスタックは次のようになります。
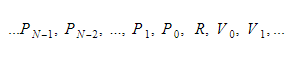
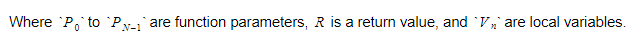
関数は戻り変数の絶対インデックスを保持し、各変数またはパラメーターはそのインデックスに関連して検出されます。
今のところ、関数を定数グローバル識別子として扱います。
これは、識別子情報として機能するクラスです。
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; ローカル変数と関数パラメーターの場合、関数indexは戻り値に関連するインデックスを返します。 グローバル識別子の場合は、絶対グローバルインデックスを返します。
compile_contextで3つの異なる識別子ルックアップがあります:
- グローバル識別子ルックアップ。コンパイル全体を通して同じであるため、
compile_contextは値によって保持されます。 -
unique_ptrとしてのローカル識別子ルックアップ。これはグローバルスコープではnullptrであり、任意の関数で初期化されます。 スコープに入るたびに、新しいローカルコンテキストは、古いコンテキストを親として初期化されます。 スコープを離れると、その親に置き換えられます。 - 生のポインタとなる関数識別子ルックアップ。 グローバルスコープでは
nullptrになり、関数の最も外側のローカルスコープと同じ値になります。
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };式ツリー
式トークンが解析されると、式ツリーに変換されます。 すべてのツリーと同様に、これもノードで構成されています。

ノードには2つの異なる種類があります。
- リーフノード。次のいずれかになります。
a)識別子
b)数字
c)文字列 - 子ノードでの操作を表す内部ノード。 子を
unique_ptrで保持します。
ノードごとに、そのタイプと、左辺値( =演算子の左側に表示される値)を返すかどうかに関する情報があります。
内部ノードが作成されると、その子の戻り型を期待する型に変換しようとします。 次の暗黙的な変換が許可されます。
- 左辺値から非左辺値
voidにするものstringへのnumber
変換が許可されていない場合、セマンティックエラーがスローされます。
ヘルパー関数と実装の詳細を除いたクラス定義は次のとおりです。
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; 関数check_conversionを除いて、メソッドの機能は自明です。 型変換規則に従って、型が渡されたtype_idおよびboolean lvalueに変換可能かどうかをチェックし、変換できない場合は例外をスローします。
ノードがstd::stringまたはdoubleで初期化されている場合、そのタイプはそれぞれstringまたはnumberになり、左辺値にはなりません。 識別子で初期化されている場合は、その識別子のタイプを想定し、識別子が定数でない場合は左辺値になります。
ただし、ノード操作で初期化された場合、そのタイプは操作に依存し、場合によってはその子のタイプに依存します。 表に式の型を書いてみましょう。 左辺値を示すために&接尾辞を使用します。 複数の式が同じ扱いになる場合は、丸括弧で囲んで追加の式を記述します。
単項演算
| 手術 | 操作タイプ | xタイプ |
| ++ x(--x) | 番号& | 番号& |
| x ++(x--) | 番号 | 番号& |
| + x(-x〜x!x) | 番号 | 番号 |
二項演算
| 手術 | 操作タイプ | xタイプ | yタイプ |
| x + y(xy x * yx / yx \ yx%y x&y x | yx ^ y x << y x >> y x && y x || y) | 番号 | 番号 | 番号 |
| x == y(x!= y x <y x> y x <= y x> = y) | 番号 | 数字または文字列 | xと同じ |
| x..y | ストリング | ストリング | ストリング |
| x = y | xと同じ | 何かの左辺値 | xと同じですが、左辺値はありません |
| x + = y(x- = yx * = yx / = yx \ = yx%= y x&= yx | = yx ^ = y x << = y x >> = y) | 番号& | 番号& | 番号 |
| x .. = y | ストリング& | ストリング& | ストリング |
| x、y | yと同じ | 空所 | なんでも |
| x [y] | xの要素タイプ | 配列型 | 番号 |
三項演算
| 手術 | 操作タイプ | xタイプ | yタイプ | zタイプ |
| x?y:z | yと同じ | 番号 | なんでも | yと同じ |
関数呼び出し
関数呼び出しに関しては、物事はもう少し複雑になります。 関数にN個の引数がある場合、関数呼び出し操作にはN + 1個の子があり、最初の子は関数自体であり、残りの子は関数の引数に対応します。
ただし、参照によって暗黙的に引数を渡すことは許可されません。 発信者には、プレフィックスとして&記号を付ける必要があります。 今のところ、これは追加の演算子ではなく、関数呼び出しの解析方法です。 アンパサンドを解析しない場合、引数が期待されるときに、 node_operation::paramと呼ばれる偽の単項演算を追加することにより、その引数から左辺値を削除します。 その操作はその子と同じタイプですが、左辺値ではありません。
次に、その呼び出し操作でノードを構築するときに、左辺値であるが関数で予期されていない引数がある場合、呼び出し元が誤ってアンパサンドを入力したことを意味するため、エラーが生成されます。 やや意外なことに、その&は、演算子として扱われる場合、式内で解析された場合に意味的に意味を持たないため、優先順位が最も低くなります。 後で変更する場合があります。
式パーサー
プログラマーの可能性についての彼の主張の1つで、有名なコンピューターサイエンスの哲学者EdsgerDijkstraはかつて次のように述べています。
「以前にBASICに触れたことのある学生に優れたプログラミングを教えることは事実上不可能です。 潜在的なプログラマーとして、彼らは再生の希望を超えて精神的に切断されています。」
ですから、BASICに触れたことがないすべての人にとって、「精神的な切断」から逃れたので、感謝してください。
残りの私たち、切断されたプログラマーは、私たちがBASICでコーディングした時代を思い出させてくれます。 積分除算に使用される演算子\がありました。 整数と浮動小数点数に別々の型がない言語では、それは非常に便利なので、同じ演算子をStorkに追加しました。 また、演算子\=を追加しました。これは、ご想像のとおり、積分除算を実行してから割り当てます。
このような演算子は、たとえばJavaScriptプログラマーに喜ばれると思います。 ダイクストラがJSの人気の高まりを見るのに十分な長さで生きていたら、彼らについて何と言うか想像さえしたくありません。
そういえば、JavaScriptで私が抱えている最大の問題の1つは、次の式の不一致です。
-
"1" - “1”は0と評価されます "1" * “1”は1と評価されます"1" / “1”は1と評価されます"1" + “1”は“11”と評価されます
ザグレブの郊外を結ぶトラムにちなんで名付けられたクロアチアのヒップホップデュオ「Tram11」には、 「1と1は2ではなく11」と大まかに解釈される曲がありました。 90年代後半にリリースされたため、JavaScriptへの参照ではありませんでしたが、この不一致をよく示しています。
これらの不一致を回避するために、文字列から数値への暗黙の変換を禁止し、連結に..演算子を追加しました(および..=代入付きの連結に)。 そのオペレーターのアイデアをどこで得たのか覚えていません。 これはBASICやPHPからのものではなく、Pythonについて何かをグーグルで検索すると背筋が冷たくなるため、「Python連結」というフレーズは検索しません。 私はヘビに対する恐怖症を抱えており、それを「連結」と組み合わせています-いいえ、ありがとう! おそらく後で、ASCIIアートのない古風なテキストベースのブラウザを使用します。
しかし、このセクションのトピックである式パーサーに戻ります。 「操車場アルゴリズム」の適応を使用します。
これは、平均的なプログラマーでさえ、問題について10分ほど考えた後に頭に浮かぶアルゴリズムです。 中置式を評価したり、逆ポーランド記法に変換したりするために使用できますが、これは行いません。
アルゴリズムの考え方は、オペランドと演算子を左から右に読み取ることです。 オペランドを読み取るときは、それをオペランドスタックにプッシュします。 次の演算子がその演算子よりも優先されるかどうかわからないため、演算子を読み取ったときにすぐに評価することはできません。 したがって、それをオペレータースタックにプッシュします。
ただし、最初に、スタックの最上位にある演算子が、今読んだ演算子よりも優先順位が高いかどうかを確認します。 その場合、オペランドスタック上のオペランドを使用して、スタックの最上位から演算子を評価します。 結果をオペランドスタックにプッシュします。 すべてを読み取るまで保持し、演算子スタックの左側にあるすべての演算子をオペランドスタックのオペランドで評価し、演算子がなくなり、オペランドが1つだけになるまで、結果をオペランドスタックにプッシュします。結果。
2つの演算子の優先順位が同じである場合、それらの演算子が左結合である場合に備えて、左側の演算子を使用します。 そうでなければ、私たちは正しいものを取ります。 同じ優先順位の2つの演算子は、異なる結合性を持つことはできません。
元のアルゴリズムも丸括弧を処理しますが、アルゴリズムがよりクリーンになるため、代わりに再帰的に処理します。
Edsger Dijkstraは、このアルゴリズムを「操車場」と名付けました。これは、鉄道の操車場の操作に似ているためです。
ただし、元の操車場アルゴリズムではエラーチェックがほとんど行われないため、無効な式が正しい式として解析される可能性があります。 したがって、演算子またはオペランドが必要かどうかをチェックするブール変数を追加しました。 オペランドが必要な場合は、単項プレフィックス演算子も解析できます。 そうすれば、無効な式がレーダーの下を通過することはなく、式の構文チェックが完了します。
まとめ
シリーズのこの部分のコーディングを始めたとき、私は式ビルダーについて書くことを計画しました。 評価できる式を作りたかったのです。 しかし、1つのブログ投稿には複雑すぎることが判明したので、半分に分割することにしました。 このパートでは、式の解析を終了しました。次の記事では、式オブジェクトの構築について説明します。
正しく思い出せば、15年ほど前、母国語の最初のバージョンを書くのに1週間かかったので、今回は何が悪かったのだろうと思います。
私が年を取り、機知に富んでいないことを否定するために、私は2歳の息子が私の暇な時間にあまりにも要求が厳しいことを非難します。
パート1と同様に、GitHubページからコードを読んだり、ダウンロードしたり、コンパイルしたりすることもできます。
