Stork, partie 2 : création d'un analyseur d'expressions
Publié: 2022-03-11Dans cette partie de notre série, nous aborderons l'un des composants les plus délicats (du moins à mon avis) du script d'un moteur de langage, qui est un élément essentiel de tout langage de programmation : l'analyseur d'expression.
Une question qu'un lecteur pourrait poser – et à juste titre – est la suivante : pourquoi n'utilisons-nous pas simplement des outils ou des bibliothèques sophistiqués, quelque chose déjà à notre disposition ?
Pourquoi n'utilisons-nous pas Lex, YACC, Bison, Boost Spirit, ou au moins des expressions régulières ?
Tout au long de notre relation, ma femme a remarqué une de mes caractéristiques que je ne peux pas nier : chaque fois que je suis confronté à une question difficile, je fais une liste. Si vous y réfléchissez, cela est parfaitement logique - j'utilise la quantité pour compenser le manque de qualité dans ma réponse.
Je vais faire la même chose maintenant.
- Je souhaite utiliser le C++ standard. Dans ce cas, ce sera C++17. Je pense que le langage est assez riche en soi, et je me bats contre l'envie d'ajouter autre chose que la bibliothèque standard dans le mélange.
- Lorsque j'ai développé mon premier langage de script, je n'utilisais aucun outil sophistiqué. J'étais sous pression et dans un délai serré, mais je ne savais pas comment utiliser Lex, YACC ou quelque chose de similaire. Par conséquent, j'ai décidé de tout développer manuellement.
- Plus tard, j'ai trouvé un blog d'un développeur de langage de programmation expérimenté, qui déconseillait d'utiliser l'un de ces outils. Il a dit que ces outils résolvent la partie la plus facile du développement du langage, donc dans tous les cas, il vous reste les choses difficiles. Je ne trouve pas ce blog en ce moment, car il l'était il y a longtemps, quand Internet et moi étions jeunes.
- En même temps, il y avait un mème qui disait : « Vous avez un problème que vous décidez de résoudre en utilisant des expressions régulières. Maintenant, vous avez deux problèmes.
- Je ne connais pas Lex, YACC, Bison ou quoi que ce soit de similaire. Je connais Boost Spirit, et c'est une bibliothèque pratique et étonnante, mais je préfère toujours avoir un meilleur contrôle sur l'analyseur.
- J'aime faire ces composants manuellement. En fait, je pourrais simplement donner cette réponse et supprimer complètement cette liste.
Le code complet est disponible sur ma page GitHub.
Itérateur de jeton
Il y a quelques changements dans le code de la partie 1.
Ce sont pour la plupart des correctifs simples et de petits changements, mais un ajout important au code d'analyse existant est la classe token_iterator . Cela nous permet d'évaluer le jeton actuel sans le supprimer du flux, ce qui est très pratique.
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; Il est initialisé avec push_back_stream , puis il peut être déréférencé et incrémenté. Il peut être vérifié avec un bool cast explicite, qui sera évalué à false lorsque le jeton actuel est égal à eof.
Langage à typage statique ou dynamique ?
Il y a une décision que je dois prendre dans cette partie : ce langage sera-t-il typé statiquement ou dynamiquement ?
Un langage typé statiquement est un langage qui vérifie les types de ses variables au moment de la compilation.
Un langage typé dynamiquement , en revanche, ne le vérifie pas lors de la compilation (s'il y a compilation, ce qui n'est pas obligatoire pour un langage typé dynamiquement) mais lors de l'exécution. Par conséquent, des erreurs potentielles peuvent vivre dans le code jusqu'à ce qu'elles soient rencontrées.
C'est un avantage évident des langages à typage statique. Tout le monde aime attraper ses erreurs le plus tôt possible. Je me suis toujours demandé quel était le plus grand avantage des langages à typage dynamique, et la réponse m'a frappé ces dernières semaines : c'est beaucoup plus facile à développer !
Le langage précédent que j'ai développé était typé dynamiquement. J'étais plus ou moins satisfait du résultat, et écrire l'analyseur d'expression n'était pas trop difficile. En gros, vous n'avez pas à vérifier les types de variables et vous vous fiez aux erreurs d'exécution, que vous codez presque spontanément.
Par exemple, si vous devez écrire l'opérateur binaire + et que vous voulez le faire pour les nombres, il vous suffit d'évaluer les deux côtés de cet opérateur en tant que nombres lors de l'exécution. Si l'un des côtés ne peut pas évaluer le nombre, vous lancez simplement une exception. J'ai même implémenté la surcharge des opérateurs en vérifiant les informations de type d'exécution des variables dans une expression, et les opérateurs faisaient partie de ces informations d'exécution.
Dans le premier langage que j'ai développé (c'est mon troisième), j'ai fait de la vérification de type au moment de la compilation, mais je n'en avais pas pleinement profité. L'évaluation de l'expression dépendait toujours des informations de type d'exécution.
Maintenant, j'ai décidé de développer un langage typé statiquement, et cela s'est avéré être une tâche beaucoup plus difficile que prévu. Cependant, comme je ne prévois pas de le compiler en un code binaire ou tout type de code d'assemblage émulé, un certain type d'informations existera implicitement dans le code compilé.
Les types
Comme minimum de types que nous devons prendre en charge, nous commencerons par ce qui suit :
- Nombres
- Cordes
- Les fonctions
- Tableaux
Bien que nous puissions les ajouter à l'avenir, nous ne prendrons pas en charge les structures (ou les classes, les enregistrements, les tuples, etc.) au début. Cependant, nous garderons à l'esprit que nous pourrons les ajouter plus tard, afin de ne pas sceller notre destin avec des décisions difficiles à changer.
Tout d'abord, je voulais définir le type comme une chaîne, qui suivra une convention. Chaque identifiant conserverait cette chaîne par valeur au moment de la compilation, et nous devrons parfois l'analyser. Par exemple, si nous encodons le type de tableau de nombres en tant que "[nombre]", nous devrons alors couper le premier et le dernier caractère afin d'obtenir un type interne, qui est "nombre" dans ce cas. C'est une très mauvaise idée si vous y réfléchissez.
Ensuite, j'ai essayé de l'implémenter en tant que classe. Cette classe aurait toutes les informations sur le type. Chaque identifiant garderait un pointeur partagé vers cette classe. Au final, j'ai pensé à avoir le registre de tous les types utilisés lors de la compilation, ainsi chaque identifiant aurait le pointeur brut vers son type.
J'ai aimé cette idée, alors nous nous sommes retrouvés avec ce qui suit :
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;Les types simples sont membres de l'énumération :
enum struct simple_type { nothing, number, string, }; Le membre d'énumération nothing n'est ici en tant qu'espace réservé pour void , que je ne peux pas utiliser car il s'agit d'un mot-clé en C++.
Les types de tableau sont représentés avec la structure ayant le seul membre de type_handle .
struct array_type { type_handle inner_type_id; }; Évidemment, la longueur du tableau ne fait pas partie de array_type , donc les tableaux se développeront dynamiquement. Cela signifie que nous nous retrouverons avec std::deque ou quelque chose de similaire, mais nous traiterons de cela plus tard.
Un type de fonction est composé de son type de retour, du type de chacun de ses paramètres et du fait que chacun de ces paramètres est passé ou non par valeur ou par référence.
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };Maintenant, nous pouvons définir la classe qui conservera ces types.
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; Les types sont conservés dans std::set , car ce conteneur est stable, ce qui signifie que les pointeurs vers ses membres sont valides même après l'insertion de nouveaux types. Il y a la fonction get_handle , qui enregistre le type passé et renvoie le pointeur vers celui-ci. Si le type est déjà enregistré, il renverra le pointeur vers le type existant. Il existe également des fonctions pratiques pour obtenir des types primitifs.
Comme pour la conversion implicite entre types, les nombres seront convertibles en chaînes. Cela ne devrait pas être dangereux, car une conversion inverse n'est pas possible et l'opérateur de concaténation de chaînes est distinct de celui d'addition de nombres. Même si cette conversion est supprimée dans les dernières étapes du développement de ce langage, elle servira bien d'exercice à ce stade. Pour cela, j'ai dû modifier l'analyseur de nombres, car il analysait toujours . comme point décimal. Il peut s'agir du premier caractère de l'opérateur de concaténation .. .
Contexte du compilateur
Lors de la compilation, différentes fonctions du compilateur doivent obtenir des informations sur le code compilé jusqu'à présent. Nous conserverons ces informations dans une classe compiler_context . Puisque nous sommes sur le point d'implémenter l'analyse d'expression, nous devrons récupérer des informations sur les identifiants que nous rencontrons.
Pendant l'exécution, nous conserverons les variables dans deux conteneurs différents. L'un d'eux sera le conteneur de variables globales, et un autre sera la pile. La pile grandira au fur et à mesure que nous appellerons des fonctions et entrerons dans des étendues. Il diminuera à mesure que nous revenons des fonctions et que nous quittons les étendues. Lorsque nous appelons une fonction, nous allons pousser les paramètres de la fonction, puis la fonction s'exécutera. Sa valeur de retour sera poussée vers le haut de la pile à sa sortie. Par conséquent, pour chaque fonction, la pile ressemblera à ceci :
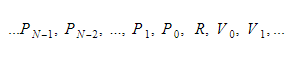
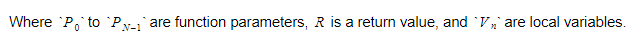
La fonction conservera l'index absolu de la variable de retour, et chaque variable ou paramètre sera trouvé par rapport à cet index.
Pour l'instant, nous traiterons les fonctions comme des identificateurs globaux constants.
Il s'agit de la classe qui sert d'informations d'identification :
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; Pour les variables locales et les paramètres de fonction, la fonction index renvoie l'index relatif à la valeur de retour. Il renvoie l'index global absolu en cas d'identificateurs globaux.
Nous aurons trois recherches d'identifiant différentes dans compile_context :
- Recherche d'identifiant global, qui
compile_contexttiendra par valeur, car il est le même tout au long de la compilation. - Recherche d'identifiant local, en tant que
unique_ptr, qui seranullptrdans la portée globale et sera initialisé dans n'importe quelle fonction. Chaque fois que nous entrons dans la portée, le nouveau contexte local sera initialisé avec l'ancien comme parent. Lorsque nous quittons la portée, elle sera remplacée par son parent. - Recherche d'identifiant de fonction, qui sera le pointeur brut. Ce sera
nullptrdans la portée globale et la même valeur que la portée locale la plus externe dans n'importe quelle fonction.
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };Arbre d'expressions
Lorsque les jetons d'expression sont analysés, ils sont convertis en arbre d'expression. Semblable à tous les arbres, celui-ci se compose également de nœuds.

Il existe deux types de nœuds différents :
- Nœuds feuilles, qui peuvent être :
a) Identifiants
b) Chiffres
c) Cordes - Les nœuds internes, qui représentent une opération sur leurs nœuds enfants. Il garde ses enfants avec
unique_ptr.
Pour chaque nœud, il y a des informations sur son type et s'il renvoie ou non une lvalue (une valeur qui peut apparaître sur le côté gauche de l'opérateur = ).
Lorsqu'un nœud interne est créé, il essaie de convertir les types de retour de ses enfants en types qu'il attend. Les conversions implicites suivantes sont autorisées :
- lvalue à non-lvalue
- N'importe quoi à
void -
numberenstring
Si la conversion n'est pas autorisée, une erreur sémantique sera renvoyée.
Voici la définition de la classe, sans quelques fonctions d'assistance et détails d'implémentation :
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; La fonctionnalité des méthodes est explicite, à l'exception de la fonction check_conversion . Il vérifiera si le type est convertible en type_id et boolean lvalue en obéissant aux règles de conversion de type et lèvera une exception si ce n'est pas le cas.
Si un nœud est initialisé avec std::string , ou double , son type sera respectivement string ou number , et ce ne sera pas une lvalue. S'il est initialisé avec un identifiant, il assumera le type de cet identifiant et sera une lvalue si l'identifiant n'est pas constant.
S'il est initialisé, cependant, avec une opération de nœud, son type dépendra de l'opération, et parfois du type de ses enfants. Écrivons les types d'expression dans le tableau. J'utiliserai le suffixe & pour désigner une lvalue. Dans les cas où plusieurs expressions ont le même traitement, j'écrirai des expressions supplémentaires entre parenthèses.
Opérations unaires
| Opération | Type d'opération | type X |
| ++x (--x) | numéro& | numéro& |
| x++ (x--) | numéro | numéro& |
| +x (-x ~x !x) | numéro | numéro |
Opérations binaires
| Opération | Type d'opération | type X | y tapez |
| x+y (xy x*yx/yx\yx%y x&y x|yx^y x<<y x>>y x&&y x||y) | numéro | numéro | numéro |
| x==y (x!=y x<y x>y x<=y x>=y) | numéro | nombre ou chaîne | identique à x |
| x..y | chaîne de caractères | chaîne de caractères | chaîne de caractères |
| x=y | identique à x | la valeur de quoi que ce soit | identique à x, sans lvalue |
| x+=y (x-=yx*=yx/=yx\=yx%=y x&=yx|=yx^=y x<<=y x>>=y) | numéro& | numéro& | numéro |
| x..=y | chaîne de caractères& | chaîne de caractères& | chaîne de caractères |
| x,y | même que y | annuler | rien |
| x[y] | type d'élément de x | type de tableau | numéro |
Opérations ternaires
| Opération | Type d'opération | type X | y tapez | type z |
| x?y:z | même que y | numéro | rien | même que y |
Appel de fonction
En ce qui concerne l'appel de fonction, les choses se compliquent un peu. Si la fonction a N arguments, l'opération d'appel de fonction a N+1 enfants, où le premier enfant est la fonction elle-même, et le reste des enfants correspond aux arguments de la fonction.
Cependant, nous n'autoriserons pas le passage implicite d'arguments par référence. Nous demanderons à l'appelant de les préfixer avec le signe & . Pour l'instant, ce ne sera pas un opérateur supplémentaire mais la façon dont l'appel de fonction est analysé. Si nous n'analysons pas l'esperluette, lorsque l'argument est attendu, nous supprimerons la lvalue-ness de cet argument en ajoutant une fausse opération unaire que nous appellerons node_operation::param . Cette opération a le même type que son enfant, mais ce n'est pas une lvalue.
Ensuite, lorsque nous construisons le nœud avec cette opération d'appel, si nous avons un argument qui est lvalue mais qui n'est pas attendu par la fonction, nous générerons une erreur, car cela signifie que l'appelant a accidentellement tapé l'esperluette. De manière quelque peu surprenante, ce & , s'il est traité comme un opérateur, aurait le moins de priorité, car il n'a pas de sens sémantiquement s'il est analysé à l'intérieur de l'expression. Nous pouvons le changer plus tard.
Analyseur d'expressions
Dans l'une de ses affirmations sur le potentiel des programmeurs, le célèbre philosophe informatique Edsger Dijkstra a dit un jour :
"Il est pratiquement impossible d'enseigner une bonne programmation à des étudiants qui ont déjà été exposés au BASIC. En tant que programmeurs potentiels, ils sont mentalement mutilés au-delà de tout espoir de régénération.
Donc, pour tous ceux d'entre vous qui n'ont pas été exposés au BASIC, soyez reconnaissants d'avoir échappé à la "mutilation mentale".
Nous autres, programmeurs mutilés, rappelons-nous le temps où nous codions en BASIC. Il y avait un opérateur \ , qui était utilisé pour la division intégrale. Dans un langage où vous n'avez pas de types séparés pour les nombres entiers et flottants, c'est très pratique, j'ai donc ajouté le même opérateur à Stork. J'ai également ajouté l'opérateur \= , qui, comme vous l'avez deviné, effectuera une division intégrale puis affectera.
Je pense que de tels opérateurs seraient appréciés par les programmeurs JavaScript, par exemple. Je ne veux même pas imaginer ce que Dijkstra en dirait s'il vivait assez longtemps pour voir la popularité croissante de JS.
En parlant de cela, l'un des plus gros problèmes que j'ai avec JavaScript est la divergence des expressions suivantes :
-
"1" - “1”est évalué à0 -
"1" * “1”est évalué à1 -
"1" / “1”est évalué à1 -
"1" + “1”est évalué à“11”
Le duo de hip-hop croate "Tram 11", du nom d'un tramway qui relie les quartiers périphériques de Zagreb, avait une chanson qui se traduit approximativement par : "Un et un ne sont pas deux, mais 11". Il est sorti à la fin des années 90, donc ce n'était pas une référence à JavaScript, mais cela illustre assez bien l'écart.
Pour éviter ces divergences, j'ai interdit la conversion implicite de chaîne en nombre, et j'ai ajouté l'opérateur .. pour la concaténation (et ..= pour la concaténation avec affectation). Je ne me souviens pas où j'ai eu l'idée de cet opérateur. Ce n'est pas de BASIC ou de PHP, et je ne chercherai pas l'expression « concaténation de Python » parce que googler quoi que ce soit à propos de Python me donne des frissons dans le dos. J'ai une phobie des serpents, et combiner cela avec la "concaténation" - non, merci ! Peut-être plus tard, avec un navigateur textuel archaïque, sans art ASCII.
Mais revenons au sujet de cette section - notre analyseur d'expression. Nous utiliserons une adaptation de "Shunting-yard Algorithm".
C'est l'algorithme qui vient à l'esprit de tout programmeur, même moyen, après avoir réfléchi au problème pendant environ 10 minutes. Il peut être utilisé pour évaluer une expression infixe ou la transformer en notation polonaise inverse, ce que nous ne ferons pas.
L'idée de l'algorithme est de lire les opérandes et les opérateurs de gauche à droite. Lorsque nous lisons un opérande, nous le poussons dans la pile des opérandes. Lorsque nous lisons un opérateur, nous ne pouvons pas l'évaluer immédiatement, car nous ne savons pas si l'opérateur suivant aura une meilleure priorité que celui-là. Par conséquent, nous le poussons vers la pile des opérateurs.
Cependant, nous vérifions d'abord si l'opérateur en haut de la pile a une meilleure priorité que celui que nous venons de lire. Dans ce cas, nous évaluons l'opérateur à partir du haut de la pile avec des opérandes sur la pile d'opérandes. Nous poussons le résultat dans la pile des opérandes. Nous le gardons jusqu'à ce que nous lisons tout, puis évaluons tous les opérateurs à gauche de la pile d'opérateurs avec les opérandes sur la pile d'opérandes, repoussant les résultats sur la pile d'opérandes jusqu'à ce qu'il ne nous reste plus d'opérateurs et avec un seul opérande, qui est le résultat.
Lorsque deux opérateurs ont la même priorité, nous prendrons celui de gauche au cas où ces opérateurs seraient associatifs à gauche ; sinon, on prend la bonne. Deux opérateurs de même priorité ne peuvent pas avoir une associativité différente.
L'algorithme d'origine traite également les parenthèses, mais nous le ferons de manière récursive à la place, car l'algorithme sera plus propre de cette façon.
Edsger Dijkstra a nommé l'algorithme "Shunting-yard" parce qu'il ressemble au fonctionnement d'une gare de triage ferroviaire.
Cependant, l'algorithme original de triage de triage ne fait presque aucune vérification d'erreur, il est donc tout à fait possible qu'une expression invalide soit analysée comme une expression correcte. Par conséquent, j'ai ajouté la variable booléenne qui vérifie si nous attendons un opérateur ou un opérande. Si nous attendons des opérandes, nous pouvons également analyser les opérateurs de préfixe unaire. De cette façon, aucune expression invalide ne peut passer sous le radar et la vérification de la syntaxe de l'expression est terminée.
Emballer
Lorsque j'ai commencé à coder pour cette partie de la série, j'avais prévu d'écrire sur le générateur d'expressions. Je voulais construire une expression qui peut être évaluée. Cependant, cela s'est avéré beaucoup trop compliqué pour un article de blog, alors j'ai décidé de le diviser en deux. Dans cette partie, nous avons conclu l'analyse des expressions, et j'écrirai sur la construction d'objets d'expression dans le prochain article.
Si je me souviens bien, il y a une quinzaine d'années, il m'a fallu un week-end pour écrire la première version de ma langue maternelle, ce qui me fait me demander ce qui n'allait pas cette fois-ci.
Dans un effort pour nier que je vieillis et que je perds de l'esprit, je reprocherai à mon fils de deux ans d'être trop exigeant pendant mon temps libre.
Comme dans la partie 1, vous êtes invités à lire, télécharger ou même compiler le code de ma page GitHub.
