Storch, Teil 2: Erstellen eines Ausdrucksparsers
Veröffentlicht: 2022-03-11In diesem Teil unserer Serie behandeln wir eine der kniffligeren (zumindest meiner Meinung nach) Komponenten beim Skripten einer Sprach-Engine, die ein wesentlicher Baustein für jede Programmiersprache ist: den Ausdrucksparser.
Eine Frage, die sich ein Leser stellen könnte – und das zu Recht –, lautet: Warum verwenden wir nicht einfach ausgeklügelte Tools oder Bibliotheken, die uns bereits zur Verfügung stehen?
Warum verwenden wir nicht Lex, YACC, Bison, Boost Spirit oder zumindest reguläre Ausdrücke?
Während unserer gesamten Beziehung ist meiner Frau eine Eigenschaft an mir aufgefallen, die ich nicht leugnen kann: Wenn ich mit einer schwierigen Frage konfrontiert werde, mache ich eine Liste. Wenn Sie darüber nachdenken, macht es absolut Sinn – ich verwende Quantität, um den Mangel an Qualität in meiner Antwort auszugleichen.
Das werde ich jetzt auch tun.
- Ich möchte Standard-C++ verwenden. In diesem Fall ist das C++17. Ich denke, die Sprache ist für sich genommen ziemlich reichhaltig, und ich kämpfe gegen den Drang an, etwas anderes als die Standardbibliothek in die Mischung aufzunehmen.
- Als ich meine erste Skriptsprache entwickelt habe, habe ich keine ausgefeilten Tools verwendet. Ich stand unter Druck und hatte eine enge Deadline, aber ich wusste nicht, wie man Lex, YACC oder ähnliches benutzt. Daher habe ich mich entschieden, alles manuell zu entwickeln.
- Später fand ich einen Blog eines erfahrenen Programmiersprachenentwicklers, der davon abriet, eines dieser Tools zu verwenden. Er sagte, diese Tools lösen den einfacheren Teil der Sprachentwicklung, so dass Sie auf jeden Fall mit den schwierigen Dingen zurückbleiben. Ich kann diesen Blog gerade nicht finden, da er vor langer Zeit war, als sowohl das Internet als auch ich jung waren.
- Gleichzeitig gab es ein Meme, das sagte: „Sie haben ein Problem, das Sie mit regulären Ausdrücken lösen möchten. Jetzt hast du zwei Probleme.“
- Ich kenne Lex, YACC, Bison oder ähnliches nicht. Ich kenne Boost Spirit und es ist eine praktische und erstaunliche Bibliothek, aber ich bevorzuge immer noch eine bessere Kontrolle über den Parser.
- Ich mache diese Komponenten gerne manuell. Eigentlich könnte ich nur diese Antwort geben und diese Liste komplett entfernen.
Der vollständige Code ist auf meiner GitHub-Seite verfügbar.
Token-Iterator
Es gibt einige Änderungen am Code von Teil 1.
Dies sind hauptsächlich einfache Korrekturen und kleine Änderungen, aber eine wichtige Ergänzung des vorhandenen Parsing-Codes ist die Klasse token_iterator . Es ermöglicht uns, das aktuelle Token auszuwerten, ohne es aus dem Stream zu entfernen, was sehr praktisch ist.
class tokens_iterator { private: push_back_stream& _stream; token _current; public: tokens_iterator(push_back_stream& stream); const token& operator*() const; const token* operator->() const; tokens_iterator& operator++(); explicit operator bool() const; }; Es wird mit push_back_stream initialisiert und kann dann dereferenziert und inkrementiert werden. Es kann mit einem expliziten Bool-Cast überprüft werden, der als falsch ausgewertet wird, wenn das aktuelle Token gleich eof ist.
Statisch oder dynamisch typisierte Sprache?
In diesem Teil muss ich eine Entscheidung treffen: Wird diese Sprache statisch oder dynamisch typisiert?
Eine statisch typisierte Sprache ist eine Sprache, die die Typen ihrer Variablen zum Zeitpunkt der Kompilierung überprüft.
Eine dynamisch typisierte Sprache hingegen überprüft dies nicht während der Kompilierung (falls es eine Kompilierung gibt, was für eine dynamisch typisierte Sprache nicht zwingend erforderlich ist), sondern während der Ausführung. Daher können potenzielle Fehler im Code leben, bis sie getroffen werden.
Dies ist ein offensichtlicher Vorteil von statisch typisierten Sprachen. Jeder möchte seine Fehler so schnell wie möglich abfangen. Ich habe mich immer gefragt, was der größte Vorteil dynamisch typisierter Sprachen ist, und die Antwort traf mich in den letzten Wochen: Es ist viel einfacher zu entwickeln!
Die vorherige Sprache, die ich entwickelt habe, war dynamisch typisiert. Ich war mit dem Ergebnis mehr oder weniger zufrieden, und das Schreiben des Ausdrucksparsers war nicht allzu schwierig. Sie müssen Variablentypen im Grunde nicht überprüfen und verlassen sich auf Laufzeitfehler, die Sie fast spontan codieren.
Wenn Sie beispielsweise den binären Operator + schreiben müssen und dies für Zahlen tun möchten, müssen Sie zur Laufzeit nur beide Seiten dieses Operators als Zahlen auswerten. Wenn eine der Seiten die Zahl nicht auswerten kann, werfen Sie einfach eine Ausnahme. Ich habe sogar das Überladen von Operatoren implementiert, indem ich die Laufzeittypinformationen von Variablen in einem Ausdruck überprüft habe, und Operatoren waren Teil dieser Laufzeitinformationen.
In der ersten Sprache, die ich entwickelt habe (dies ist meine dritte), habe ich zum Zeitpunkt der Kompilierung eine Typüberprüfung durchgeführt, aber ich hatte nicht den vollen Vorteil daraus gezogen. Die Ausdrucksauswertung war immer noch von den Laufzeittypinformationen abhängig.
Jetzt entschied ich mich, eine statisch typisierte Sprache zu entwickeln, und es stellte sich als viel schwieriger heraus als erwartet. Da ich jedoch nicht vorhabe, es in einen Binärcode oder irgendeinen emulierten Assemblercode zu kompilieren, wird implizit eine Art von Information im kompilierten Code vorhanden sein.
Typen
Als absolutes Minimum an Typen, die wir unterstützen müssen, beginnen wir mit den folgenden:
- Zahlen
- Saiten
- Funktionen
- Arrays
Obwohl wir sie in Zukunft hinzufügen können, werden wir zu Beginn keine Strukturen (oder Klassen, Datensätze, Tupel usw.) unterstützen. Wir werden jedoch bedenken, dass wir sie später hinzufügen können, damit wir unser Schicksal nicht mit Entscheidungen besiegeln, die schwer zu ändern sind.
Zuerst wollte ich den Typ als String definieren, der einigen Konventionen folgt. Jeder Bezeichner würde diese Zeichenfolge zum Zeitpunkt der Kompilierung als Wert behalten, und wir müssen sie manchmal analysieren. Wenn wir beispielsweise den Typ des Zahlenarrays als „[Zahl]“ codieren, müssen wir das erste und das letzte Zeichen kürzen, um einen inneren Typ zu erhalten, der in diesem Fall „Zahl“ ist. Es ist eine ziemlich schlechte Idee, wenn man darüber nachdenkt.
Dann habe ich versucht, es als Klasse zu implementieren. Diese Klasse hätte alle Informationen über den Typ. Jeder Bezeichner würde einen gemeinsam genutzten Zeiger auf diese Klasse behalten. Am Ende dachte ich darüber nach, die Registrierung aller Typen während der Kompilierung zu verwenden, sodass jeder Bezeichner den rohen Zeiger auf seinen Typ haben würde.
Diese Idee gefiel mir, also kamen wir zu folgendem Ergebnis:
using type = std::variant<simple_type, array_type, function_type>; using type_handle = const type*;Einfache Typen sind Mitglieder der Aufzählung:
enum struct simple_type { nothing, number, string, }; Enumerationsmember nothing steht hier als Platzhalter für void , den ich nicht verwenden kann, da es sich um ein Schlüsselwort in C++ handelt.
Array-Typen werden mit der Struktur dargestellt, die das einzige Mitglied von type_handle .
struct array_type { type_handle inner_type_id; }; Offensichtlich ist die Array-Länge kein Teil von array_type , sodass Arrays dynamisch wachsen. Das bedeutet, dass wir am Ende bei std::deque oder etwas Ähnlichem landen werden, aber wir werden uns später damit befassen.
Ein Funktionstyp besteht aus seinem Rückgabetyp, dem Typ jedes seiner Parameter und ob jeder dieser Parameter als Wert oder als Referenz übergeben wird.
struct function_type { struct param { type_handle type_id; bool by_ref; }; type_handle return_type_id; std::vector<param> param_type_id; };Jetzt können wir die Klasse definieren, die diese Typen behält.
class type_registry { private: struct types_less{ bool operator()(const type& t1, const type& t2) const; }; std::set<type, types_less> _types; static type void_type; static type number_type; static type string_type; public: type_registry(); type_handle get_handle(const type& t); static type_handle get_void_handle() { return &void_type; } static type_handle get_number_handle() { return &number_type; } static type_handle get_string_handle() { return &string_type; } }; Typen werden in std::set , da dieser Container stabil ist, was bedeutet, dass Zeiger auf seine Mitglieder auch nach dem Einfügen neuer Typen gültig sind. Es gibt die Funktion get_handle , die den übergebenen Typ registriert und den Zeiger darauf zurückgibt. Wenn der Typ bereits registriert ist, wird der Zeiger auf den vorhandenen Typ zurückgegeben. Es gibt auch praktische Funktionen, um primitive Typen zu erhalten.
Bei der impliziten Konvertierung zwischen Typen können Zahlen in Zeichenfolgen konvertiert werden. Es sollte nicht gefährlich sein, da eine Rückkonvertierung nicht möglich ist und der Operator für die Stringverkettung sich von dem für die Zahlenaddition unterscheidet. Selbst wenn diese Konvertierung in den späteren Stadien der Entwicklung dieser Sprache entfernt wird, wird sie an dieser Stelle gut als Übung dienen. Zu diesem Zweck musste ich den Zahlenparser ändern, da er immer geparst hat . als Dezimalpunkt. Es kann das erste Zeichen des Verkettungsoperators sein .. .
Compiler-Kontext
Während der Kompilierung müssen verschiedene Compilerfunktionen Informationen über den bisher kompilierten Code erhalten. Wir werden diese Informationen in einer Klasse compiler_context . Da wir im Begriff sind, die Ausdrucksanalyse zu implementieren, müssen wir Informationen über die Kennungen abrufen, auf die wir stoßen.
Während der Laufzeit halten wir Variablen in zwei verschiedenen Containern. Einer davon ist der globale Variablencontainer und ein anderer der Stack. Der Stapel wird wachsen, wenn wir Funktionen aufrufen und Bereiche eingeben. Es wird schrumpfen, wenn wir von Funktionen zurückkehren und Bereiche verlassen. Wenn wir eine Funktion aufrufen, drücken wir Funktionsparameter, und dann wird die Funktion ausgeführt. Sein Rückgabewert wird beim Verlassen an die Spitze des Stapels geschoben. Daher sieht der Stack für jede Funktion wie folgt aus:
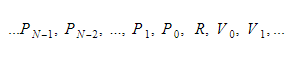
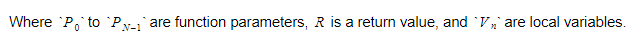
Die Funktion behält den absoluten Index der Rückgabevariablen bei, und jede Variable oder jeder Parameter wird relativ zu diesem Index gefunden.
Im Moment behandeln wir Funktionen als konstante globale Bezeichner.
Dies ist die Klasse, die als Kennungsinformation dient:
class identifier_info { private: type_handle _type_id; size_t _index; bool _is_global; bool _is_constant; public: identifier_info(type_handle type_id, size_t index, bool is_global, bool is_constant); type_handle type_id() const; size_t index() const; bool is_global() const; bool is_constant() const; }; Bei lokalen Variablen und Funktionsparametern gibt Funktionsindex den index relativ zum Rückgabewert zurück. Bei globalen Bezeichnern wird der absolute globale Index zurückgegeben.
Wir haben drei verschiedene Identifier-Lookups in compile_context :
- Suche nach globalen Kennungen, die
compile_contextnach Wert halten, da sie während der gesamten Kompilierung gleich sind. - Lokale Bezeichnersuche als
unique_ptr, die im globalen Bereichnullptrist und in jeder Funktion initialisiert wird. Immer wenn wir den Gültigkeitsbereich betreten, wird der neue lokale Kontext mit dem alten als übergeordnetem Kontext initialisiert. Wenn wir den Gültigkeitsbereich verlassen, wird er durch seinen übergeordneten ersetzt. - Nachschlagen der Funktionskennung, die der Rohzeiger sein wird. Es ist
nullptrim globalen Gültigkeitsbereich und derselbe Wert wie der äußerste lokale Gültigkeitsbereich in jeder Funktion.
class compiler_context { private: global_identifier_lookup _globals; function_identifier_lookup* _params; std::unique_ptr<local_identifier_lookup> _locals; type_registry _types; public: compiler_context(); type_handle get_handle(const type& t); const identifier_info* find(const std::string& name) const; const identifier_info* create_identifier(std::string name, type_handle type_id, bool is_constant); const identifier_info* create_param(std::string name, type_handle type_id); void enter_scope(); void enter_function(); bool leave_scope(); };Ausdrucksbaum
Wenn Ausdruckstoken analysiert werden, werden sie in eine Ausdrucksbaumstruktur konvertiert. Wie alle Bäume besteht auch dieser aus Knoten.

Es gibt zwei verschiedene Arten von Knoten:
- Blattknoten, die sein können:
a) Identifikatoren
b) Zahlen
c) Saiten - Innere Knoten, die eine Operation auf ihren untergeordneten Knoten darstellen. Es hält seine Kinder mit
unique_ptr.
Für jeden Knoten gibt es Informationen über seinen Typ und ob er einen Lvalue zurückgibt oder nicht (ein Wert, der auf der linken Seite des = -Operators erscheinen kann).
Wenn ein innerer Knoten erstellt wird, versucht er, Rückgabetypen seiner untergeordneten Knoten in Typen zu konvertieren, die er erwartet. Die folgenden impliziten Konvertierungen sind zulässig:
- Lvalue zu Nicht-Lvalue
- Alles zu
void -
numberzustring
Wenn die Konvertierung nicht erlaubt ist, wird ein semantischer Fehler ausgegeben.
Hier ist die Klassendefinition ohne einige Hilfsfunktionen und Implementierungsdetails:
enum struct node_operation { ... }; using node_value = std::variant< node_operation, std::string, double, identifier >; struct node { private: node_value _value; std::vector<node_ptr> _children; type_handle _type_id; bool _lvalue; public: node( compiler_context& context, node_value value, std::vector<node_ptr> children ); const node_value& get_value() const; const std::vector<node_ptr>& get_children() const; type_handle get_type_id() const; bool is_lvalue() const; void check_conversion(type_handle type_id, bool lvalue); }; Die Funktionsweise von Methoden ist bis auf die Funktion check_conversion . Es prüft, ob der Typ in die übergebene type_id und den booleschen lvalue konvertierbar ist, indem es die Typkonvertierungsregeln befolgt, und löst eine Ausnahme aus, wenn dies nicht der Fall ist.
Wenn ein Knoten mit std::string oder double initialisiert wird, ist sein Typ string bzw. number und kein Lvalue. Wenn es mit einem Bezeichner initialisiert wird, nimmt es den Typ dieses Bezeichners an und ist ein lvalue, wenn der Bezeichner nicht konstant ist.
Wenn es jedoch mit einer Knotenoperation initialisiert wird, hängt sein Typ von der Operation und manchmal vom Typ seiner Kinder ab. Lassen Sie uns die Ausdruckstypen in die Tabelle schreiben. Ich werde das Suffix & verwenden, um einen lvalue zu bezeichnen. In Fällen, in denen mehrere Ausdrücke die gleiche Behandlung haben, schreibe ich zusätzliche Ausdrücke in runde Klammern.
Unäre Operationen
| Operation | Operationstyp | x-Typ |
| ++x (--x) | Anzahl& | Anzahl& |
| x++ (x--) | Anzahl | Anzahl& |
| +x (-x ~x !x) | Anzahl | Anzahl |
Binäre Operationen
| Operation | Operationstyp | x-Typ | y-Typ |
| x+y (xy x*yx/yx\yx%y x&y x|yx^y x<<y x>>y x&&y x||y) | Anzahl | Anzahl | Anzahl |
| x==y (x!=y x<y x>y x<=y x>=y) | Anzahl | Zahl oder Zeichenfolge | gleich x |
| x..y | Schnur | Schnur | Schnur |
| x=y | gleich x | Wert von irgendetwas | wie x, ohne lvalue |
| x+=y (x-=yx*=yx/=yx\=yx%=y x&=yx|=yx^=y x<<=y x>>=y) | Anzahl& | Anzahl& | Anzahl |
| x..=y | Zeichenfolge& | Zeichenfolge& | Schnur |
| x, y | dasselbe wie y | Leere | irgendetwas |
| x[y] | Elementtyp von x | Array-Typ | Anzahl |
Ternäre Operationen
| Operation | Operationstyp | x-Typ | y-Typ | z-Typ |
| x?y:z | dasselbe wie y | Anzahl | irgendetwas | dasselbe wie y |
Funktionsaufruf
Beim Funktionsaufruf wird es etwas komplizierter. Wenn die Funktion N Argumente hat, hat die Funktionsaufrufoperation N+1 Kinder, wobei das erste Kind die Funktion selbst ist und die restlichen Kinder den Funktionsargumenten entsprechen.
Wir werden jedoch nicht zulassen, dass Argumente implizit als Referenz übergeben werden. Wir verlangen, dass der Anrufer ihm das & -Zeichen voranstellt. Das ist vorerst kein zusätzlicher Operator, sondern die Art und Weise, wie der Funktionsaufruf geparst wird. Wenn wir das kaufmännische Und nicht analysieren und das Argument erwartet wird, entfernen wir die lvalue-ness aus diesem Argument, indem wir eine gefälschte unäre Operation hinzufügen, die wir node_operation::param nennen. Diese Operation hat den gleichen Typ wie ihr untergeordnetes Element, ist aber kein Lvalue.
Wenn wir dann den Knoten mit dieser Aufrufoperation erstellen und ein Argument haben, das lvalue ist, aber nicht von der Funktion erwartet wird, generieren wir einen Fehler, da dies bedeutet, dass der Aufrufer versehentlich das kaufmännische Und eingegeben hat. Etwas überraschend ist, dass & , wenn es als Operator behandelt wird, den geringsten Vorrang hat, da es semantisch nicht die Bedeutung hat, wenn es innerhalb des Ausdrucks geparst wird. Wir können es später ändern.
Ausdrucksparser
In einer seiner Behauptungen über das Potenzial von Programmierern sagte der berühmte Informatikphilosoph Edsger Dijkstra einmal:
„Es ist praktisch unmöglich, Schülern, die zuvor mit BASIC in Berührung gekommen sind, gutes Programmieren beizubringen. Als potenzielle Programmierer sind sie geistig verstümmelt, ohne Hoffnung auf Regeneration.“
Also, für alle von Ihnen, die BASIC noch nicht kennengelernt haben – seien Sie dankbar, dass Sie der „geistigen Verstümmelung“ entkommen sind.
Der Rest von uns, verstümmelte Programmierer, erinnert uns an die Tage, als wir in BASIC programmiert haben. Es gab einen Operator \ , der zur ganzzahligen Division verwendet wurde. In einer Sprache, in der es keine getrennten Typen für Ganz- und Gleitkommazahlen gibt, ist das ziemlich praktisch, also habe ich Stork denselben Operator hinzugefügt. Ich habe auch den Operator \= hinzugefügt, der, wie Sie vermutet haben, eine ganzzahlige Division durchführt und dann zuweist.
Ich denke, solche Operatoren würden zum Beispiel von JavaScript-Programmierern geschätzt. Ich möchte mir gar nicht vorstellen, was Dijkstra über sie sagen würde, wenn er lange genug leben würde, um die steigende Popularität von JS zu sehen.
Apropos, eines der größten Probleme, die ich mit JavaScript habe, ist die Diskrepanz der folgenden Ausdrücke:
-
"1" - “1”ergibt0 -
"1" * “1”ergibt1 -
"1" / “1”ergibt1 -
"1" + “1”ergibt“11”
Das kroatische Hip-Hop-Duo „Tram 11“, benannt nach einer Straßenbahn, die die Außenbezirke von Zagreb verbindet, hatte ein Lied, das grob übersetzt so lautet: „Eins und eins sind nicht zwei, sondern 11.“ Es kam Ende der 90er heraus, war also kein Verweis auf JavaScript, aber es veranschaulicht die Diskrepanz ziemlich gut.
Um diese Diskrepanzen zu vermeiden, habe ich die implizite Konvertierung von String in Zahl verboten und den Operator .. für die Verkettung (und ..= für die Verkettung mit Zuweisung) hinzugefügt. Ich weiß nicht mehr, woher ich die Idee für diesen Operator hatte. Es ist nicht von BASIC oder PHP, und ich werde nicht nach dem Ausdruck „Python-Verkettung“ suchen, weil es mir kalt den Rücken hinunterläuft, wenn ich irgendetwas über Python google. Ich habe eine Schlangenphobie und kombiniere das mit „Verkettung“ – nein danke! Vielleicht später, mit einem archaischen textbasierten Browser, ohne ASCII-Art.
Aber zurück zum Thema dieses Abschnitts – unserem Ausdrucksparser. Wir werden eine Adaption des „Rangierbahnhofalgorithmus“ verwenden.
Das ist der Algorithmus, der jedem selbst durchschnittlichen Programmierer in den Sinn kommt, nachdem er ungefähr 10 Minuten über das Problem nachgedacht hat. Es kann verwendet werden, um einen Infix-Ausdruck auszuwerten oder ihn in die umgekehrte polnische Notation umzuwandeln, was wir nicht tun werden.
Die Idee des Algorithmus ist es, Operanden und Operatoren von links nach rechts zu lesen. Wenn wir einen Operanden lesen, schieben wir ihn auf den Operandenstapel. Wenn wir einen Operator lesen, können wir ihn nicht sofort auswerten, da wir nicht wissen, ob der folgende Operator eine bessere Priorität als dieser hat. Daher verschieben wir es auf den Operator-Stack.
Wir prüfen jedoch zuerst, ob der Operator an der Spitze des Stapels eine bessere Priorität hat als der, den wir gerade gelesen haben. In diesem Fall werten wir den Operator von der Spitze des Stapels mit Operanden auf dem Operandenstapel aus. Wir schieben das Ergebnis auf den Operandenstapel. Wir behalten es, bis wir alles gelesen haben und werten dann alle Operatoren auf der linken Seite des Operator-Stacks mit den Operanden auf dem Operanden-Stack aus, wobei wir die Ergebnisse zurück auf den Operanden-Stack schieben, bis wir keine Operatoren mehr haben und nur noch einen Operanden haben, was ist das Ergebnis.
Wenn zwei Operatoren denselben Vorrang haben, nehmen wir den linken, falls diese Operatoren linksassoziativ sind; ansonsten nehmen wir den richtigen. Zwei Operatoren mit derselben Priorität können keine unterschiedliche Assoziativität haben.
Der ursprüngliche Algorithmus behandelt auch runde Klammern, aber wir werden es stattdessen rekursiv tun, da der Algorithmus auf diese Weise sauberer wird.
Edsger Dijkstra nannte den Algorithmus „Rangierbahnhof“, weil er dem Betrieb eines Eisenbahn-Rangierbahnhofs ähnelt.
Der ursprüngliche Rangierbahnhofalgorithmus führt jedoch fast keine Fehlerprüfung durch, sodass es durchaus möglich ist, dass ein ungültiger Ausdruck als korrekt geparst wird. Daher habe ich die boolesche Variable hinzugefügt, die prüft, ob wir einen Operator oder einen Operanden erwarten. Wenn wir Operanden erwarten, können wir auch unäre Präfixoperatoren parsen. Auf diese Weise kann kein ungültiger Ausdruck unter das Radar gelangen, und die Ausdruckssyntaxprüfung ist abgeschlossen.
Einpacken
Als ich anfing, für diesen Teil der Serie zu programmieren, hatte ich vor, über den Expression Builder zu schreiben. Ich wollte einen Ausdruck erstellen, der ausgewertet werden kann. Es stellte sich jedoch als viel zu kompliziert für einen Blogbeitrag heraus, also beschloss ich, es in zwei Hälften zu teilen. In diesem Teil haben wir das Parsen von Ausdrücken abgeschlossen, und ich werde im nächsten Artikel über das Erstellen von Ausdrucksobjekten schreiben.
Wenn ich mich richtig erinnere, brauchte ich vor etwa 15 Jahren ein Wochenende, um die erste Version meiner Muttersprache zu schreiben, und ich frage mich, was diesmal schief gelaufen ist.
In dem Versuch zu leugnen, dass ich älter und weniger geistreich werde, werde ich meinem zweijährigen Sohn die Schuld dafür geben, dass er in meiner Freizeit zu anspruchsvoll ist.
Wie in Teil 1 können Sie den Code gerne von meiner GitHub-Seite lesen, herunterladen oder sogar kompilieren.
