R中的多元線性回歸[帶圖表和示例]

作為一名數據科學家，您經常被要求在許多項目中進行預測分析。 分析是一種統計方法，用於建立因變量與一組自變量之間的關係。 整個概念可以稱為線性回歸，它基本上有兩種類型：簡單線性回歸和多元線性回歸。

R 是數據科學和分析方面最重要的語言之一， R 中的多元線性回歸也是如此。 它描述了單個響應變量 Y 線性依賴於多個預測變量的場景。

什麼是線性回歸？

線性回歸模型用於顯示或預測一個 因變量和自變量。 當回歸分析中使用兩個或多個自變量時，該模型不是簡單的線性而是多元回歸模型。

簡單線性回歸用於通過使用另一個變量來預測一個變量的值。 一條直線用線性回歸表示兩個變量之間的關係。

在多元回歸中，因變量與兩個或多個自變量之間存在線性關係。 這種關係也可以是非線性的，因變量和自變量不會遵循一條直線。

多元線性回歸模型預測的圖示

線性和非線性回歸用於跟踪使用兩個或多個變量的響應。 非線性回歸是根據反複試驗的假設創建的，並且相對難以執行。

什麼是多元線性回歸？

多元線性回歸是一種統計分析技術，用於根據兩個或多個變量預測變量的結果。 它是線性回歸的擴展，也稱為多元回歸。 要預測的變量是因變量，用於預測因變量值的變量稱為自變量或解釋變量。

多元線性回歸使分析師能夠確定模型的變化和每個自變量的相對貢獻。 多元回歸有兩種類型，線性回歸和非線性回歸。

多元回歸公式

具有三個預測變量 (x) 預測變量 y 的多元回歸表示為以下等式：

y = z0 + z1*x1 + z2*x2 + z3*x3

“z”值代表回歸權重，是beta 係數。 它們是預測變量和結果之間的關聯。

• yi是因變量或預測變量
• z0是y截距，即x1和x2為0時y的值
• z1和z2是回歸係數，分別表示與x1和x2的一個單位變化相關的 y 變化。

多元線性回歸的假設

我們已經知道了關於多元回歸和基本公式的簡介。 但是，有一些假設是多元線性回歸所基於的，具體如下：

一世。 因變量和自變量之間的關係

因變量與每個自變量線性相關。 為了檢查線性關係，創建了一個散點圖並觀察其線性。 如果散點圖關係是非線性的，則執行非線性回歸，或使用統計軟件傳輸數據。

ii. 自變量相關性不大

數據不應顯示多重共線性，這種情況發生在自變量相互高度相關的情況下。 這將在提取導致因變量方差的特定變量時產生問題。

iii. 殘差是常數

多元線性回歸假設其餘變量的誤差在線性模型的每個點上都相似。 這被稱為同方差性。 當數據分析完成時，標準殘差與預測值的關係被繪製出來，以確定這些點是否正確分佈在自變量的值上。

iv. 觀察獨立

觀測值應該是相互的，殘差值應該是獨立的。 Durbin Watson 統計數據最適合這一點。

該方法顯示從 0 到 4 的值，其中 0 到 2 之間的值表示正自相關，從 2 到 4 表示負自相關。 中點值為 2，表示不存在自相關。

v.多元正態性

多元正態性發生在正態分佈的殘差上。 對於這個假設，觀察殘差值是如何分佈的。 它可以使用兩種方法進行測試，

· 顯示疊加正態曲線的直方圖和

· 正態概率圖法。

應用多元線性回歸的實例

從分析師的角度來看，多元線性回歸是一個非常重要的方面。 以下是該概念適用的一些示例：

一世。 由於因變量的值與自變量相關，因此使用多元回歸來預測作物在特定降雨、溫度和肥料水平下的預期產量。

ii. 多元線性回歸分析也用於預測趨勢和未來值。 這對於預測從現在起六個月內的黃金價格特別有用。

iii. 在一個特定的例子中，UBER 司機所行駛的距離與司機的年齡和司機的經驗年數之間的關係被去掉了。 在這個回歸中，因變量是 UBER 司機覆蓋的距離。 自變量是駕駛員的年齡和駕駛經驗的年數。

iv. 另一個例子是使用多元回歸分析來尋找一個班級學生的 GPA 與他們學習的小時數和學生身高之間的關係。 該回歸中的因變量是 GPA，自變量是學習時間和學生的身高。

v. 一個組織中一組員工的工資與組織工作年限之間的關係可以通過回歸分析確定員工年齡。 該回歸的因變量是工資，自變量是員工的經驗和年齡。

另請閱讀：您應該了解的機器學習中的 6 種回歸模型

R中的多元線性回歸

可以通過多種方式執行多元線性回歸，但通常通過統計軟件完成。 最常用的軟件之一是 R，它免費、強大且易於使用。 我們將首先學習使用 R 執行回歸的步驟，然後是一個清晰理解的示例。

在 R 中執行多重回歸的步驟

1. 數據採集： 收集要在預測中使用的數據。
2. R 中的數據捕獲：使用代碼捕獲數據並導入 CSV 文件
3. 用 R 檢查數據線性： 確保因變量和自變量之間存在線性關係非常重要。 可以使用散點圖或 R 中的代碼來完成
4. 在 R 中應用多元線性回歸： 使用代碼在 R 中應用多元線性回歸以獲得一組係數。
5. 使用 R 進行預測： 最後確定預測值。

R中的多重回歸實現

當公共衛生研究人員在一定數量的地方進行調查以收集有關吸煙人口、上班人員和心髒病患者的數據時，我們將了解 R 是如何實施的。

R中多元線性回歸的分步指南：

一世。 加載 heart.data 數據集並運行以下代碼

lm<-lm(heart.disease ~ 騎車 + 吸煙, data = heart.data)

數據集心臟。 數據使用“lm()”（線性模型的方程）計算自變量騎自行車和吸煙對因變量心髒病的影響。

ii. 解釋結果

使用 summary() 函數查看模型的結果：

摘要（heart.disease.lm）

該函數將從線性模型中獲得的最重要的參數放入一個表格中，如下所示：

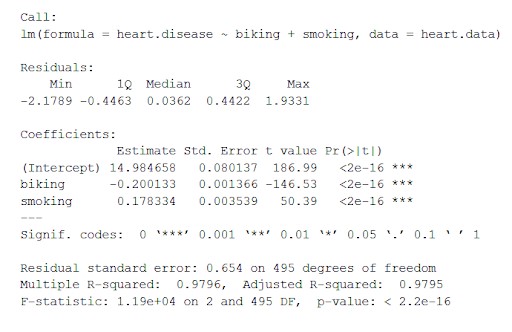
從這個表中我們可以推斷：

• “呼叫”的公式，
• 模型的殘差（“殘差”）。 如果殘差大致以零為中心並且在任一側具有相似的散佈（中位數 0.03，最小和最大 -2 和 2），則該模型符合異方差假設。
• 模型的回歸係數（“係數”）。

係數表的第 1 行（截距）：這是回歸方程的 y 截距，用於了解估計的截距以插入回歸方程並預測因變量值。

心髒病 = 15 + (-0.2*騎自行車) + (0.178*吸煙) ± e

與多重回歸相關的一些術語

一世。 Estimate Column ：估計效果，也稱為回歸係數或r2值。 估計表明，騎自行車上班每增加 1%，心髒病發病率就會降低 0.2%，而吸煙人數每增加 1%，心髒病發病率就會增加 0.17%。

ii. Std.error ：顯示標準錯誤 的估計。 這個數字顯示了回歸係數估計值的變化。

iii. t 值：顯示檢驗統計量。 它是來自雙邊t-test的t值。

iv. Pr( > | t | ) : 它是p值，表示t值出現的概率。

報告結果

我們應該包括估計效果、標準估計誤差和p值。

在上面的例子中，發現騎自行車上班的頻率與心髒病之間的顯著關係以及吸煙和心髒病的頻率之間的顯著關係為 p < 0.001。

騎自行車每增加 1%，心髒病發病率就會降低 0.2%（或 ± 0.0014）。 吸煙每增加 1%，心髒病發病率增加 0.178%（或 ±0.0035）。

結果的圖形表示

多個自變量對因變量的影響可以在圖表中顯示。 在這種情況下，只能在 x 軸上繪製一個自變量。

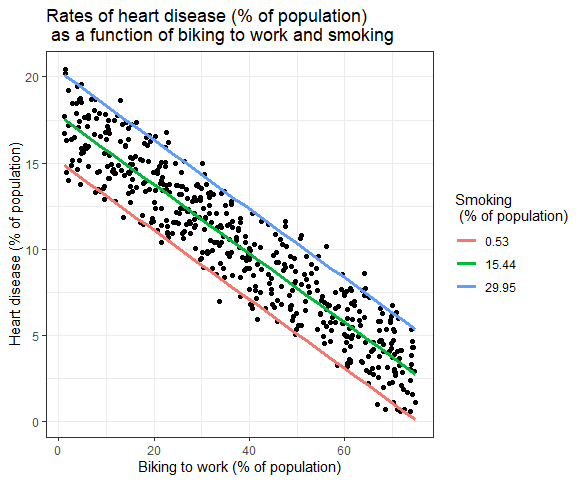
多元線性回歸：圖形表示

在這裡，繪製了因變量（心髒病）的預測值與騎自行車上班的人數百分比的觀察值之間的關係。

對於吸煙對自變量的影響，計算預測值，在最小、平均和最大吸煙率下保持吸煙不變。

另請閱讀：線性回歸與。 邏輯回歸：線性回歸和邏輯回歸之間的區別

最後的話

這標誌著這篇博文的結束。 我們已盡最大努力向您解釋多元線性回歸的概念以及如何實現 R 中的多元回歸以簡化預測分析。

如果您熱衷於支持您的數據科學之旅並學習 R 和許多其他語言的更多概念以加強您的職業生涯，請加入upGrad 。 我們提供數據科學高級認證計劃，該計劃專為在職專業人士設計，包括 300 多個小時的學習和持續的指導。