Rの重回帰[グラフと例を使用]

データサイエンティストとして、多くのプロジェクトで予測分析を行うように頻繁に求められます。 分析は、従属変数と一連の独立変数の間の関係を確立するための統計的アプローチです。 この概念全体は線形回帰と呼ぶことができ、基本的に2つのタイプがあります。単純回帰と重回帰です。

Rは、データサイエンスと分析の観点から最も重要な言語の1つであり、 Rの重回帰は価値を保持します。 これは、単一の応答変数Yが複数の予測変数に線形に依存するシナリオを説明しています。

線形回帰とは何ですか？

線形回帰モデルは、 従属変数と独立変数。 回帰分析で使用される独立変数が2つ以上ある場合、モデルは単純な線形ではなく、重回帰モデルです。

単純線形回帰は、別の変数を使用して1つの変数の値を予測するために使用されます。 直線は、線形回帰による2つの変数間の関係を表します。

重回帰では、従属変数と2つ以上の独立変数の間に線形関係があります。 関係は非線形である可能性もあり、従属変数と独立変数は直線に従わないでしょう。

複数の線形回帰モデルの予測の図解

線形および非線形回帰は、2つ以上の変数を使用して応答を追跡するために使用されます。 非線形回帰は試行錯誤の仮定から作成され、実行するのは比較的困難です。

重回帰とは何ですか？

重回帰は、2つ以上の変数に基づいて変数の結果を予測するために使用される統計分析手法です。 これは線形回帰の拡張であり、重回帰としても知られています。 予測される変数は従属変数であり、従属変数の値を予測するために使用される変数は、独立変数または説明変数と呼ばれます。

重回帰により、分析者はモデルの変動と各独立変数の相対的な寄与を判断できます。 重回帰には、線形回帰と非線形回帰の2つのタイプがあります。

重回帰式

変数yを予測する3つの予測変数（x）を使用した重回帰は、次の方程式で表されます。

y = z0 + z1 * x1 + z2 * x2 + z3 * x3

「z」値は回帰の重みを表し、ベータ係数です。 これらは、予測変数と結果の間の関連付けです。

• yiは従属変数または予測変数です
• z0はy切片です。つまり、x1とx2が0のときのyの値です。
• z1とz2は、それぞれx1とx2の1単位の変化に関連するyの変化を表す回帰係数です。

重回帰の仮定

重回帰と基本的な式についての簡単な説明を知っています。 ただし、重回帰が以下のように詳細に基づいているいくつかの仮定があります。

私。 従属変数と独立変数の関係

従属変数は、各独立変数と線形に関連しています。 線形関係を確認するために、散布図が作成され、線形性が観察されます。 散布図の関係が非線形の場合は、非線形回帰が実行されるか、統計ソフトウェアを使用してデータが転送されます。

ii。 独立変数はあまり相関していません

データは多重共線性を表示するべきではありません。これは、独立変数が互いに高度に相関している場合に発生します。 これにより、従属変数の分散に寄与する特定の変数をフェッチする際に問題が発生します。

iii。 残差分散は一定です

重回帰は、残りの変数の誤差が線形モデルの各点で類似していることを前提としています。 これは等分散性として知られています。 データ分析が行われると、予測値に対する標準残差がプロットされ、ポイントが独立変数の値に適切に分散されているかどうかが判断されます。

iv。 観察の独立性

観測値は相互に関連している必要があり、残差値は独立している必要があります。 ダービンワトソン統計はこれに最適です。

この方法では、0〜4の値が表示されます。ここで、0〜2の値は正の自己相関を示し、2〜4の値は負の自己相関を示します。 中間点である値2は、自己相関がないことを示しています。

v。多変量正規性

多変量正規性は、正規分布の残差で発生します。 この仮定では、残差の値がどのように分布しているかが観察されます。 2つの方法を使用してテストできます。

・重ね合わせた正規曲線を示すヒストグラムと

・正規確率プロット法。

重回帰が適用されるインスタンス

重回帰は、アナリストの観点から非常に重要な側面です。 概念を適用できる例のいくつかを次に示します。

私。 従属変数の値は独立変数と相関しているため、重回帰を使用して、特定の降雨量、気温、および肥料レベルでの作物の予想収量を予測します。

ii。 多重線形回帰分析は、傾向と将来の価値を予測するためにも使用されます。 これは、今から6か月後の金の価格を予測するのに特に役立ちます。

iii。 特定の例では、UBERドライバーがカバーする距離とドライバーの年齢、およびドライバーの経験年数との関係が示されています。 この回帰では、従属変数は UBERドライバーがカバーする距離。 独立変数は、ドライバーの年齢と運転経験年数です。

iv。 あるクラスの学生のGPAと、彼らが勉強する時間数および学生の身長との関係を見つけるために重回帰分析が使用される別の例。 この回帰の従属変数はGPAであり、独立変数は学習時間数と生徒の身長です。

v。組織内の従業員グループの給与と組織化の年数との関係は、回帰分析を使用して決定できます。 この回帰の従属変数は給与であり、独立変数は従業員の経験と年齢です。

また読む：あなたが知っておくべき機械学習の6種類の回帰モデル

Rの重回帰

重回帰を実行する方法はたくさんありますが、通常は統計ソフトウェアを介して実行されます。 最も使用されているソフトウェアの1つは、無料で強力で、簡単に入手できるRです。 最初にRを使用して回帰を実行する手順を学習し、次に明確な理解の例を学習します。

Rで重回帰を実行する手順

1. データ収集： 予測に使用されるデータが収集されます。
2. Rでのデータキャプチャ：コードを使用してデータをキャプチャし、CSVファイルをインポートします
3. Rを使用したデータの線形性の確認： 従属変数と独立変数の間に線形関係が存在することを確認することが重要です。 これは、散布図またはRのコードを使用して実行できます。
4. Rに重回帰を適用する： コードを使用してRに重回帰を適用し、係数のセットを取得します。
5. Rで予測する： 予測値は最後に決定されます。

Rでの重回帰の実装

公衆衛生研究者が特定の場所でRを実施し、喫煙者、職場への出張者、心臓病患者のデータを収集することで、Rがどのように実施されるかを理解します。

Rでの重回帰のステップバイステップガイド：

私。 heart.dataデータセットをロードし、次のコードを実行します

lm <-lm（heart.disease〜自転車+喫煙、データ= heart.data）

データセットの心臓部。 データは、「lm（）」（線形モデルの方程式）を使用して、従属変数の心臓病に対する独立変数の自転車と喫煙の影響を計算します。

ii。 結果の解釈

summary（）関数を使用して、モデルの結果を表示します。

要約（heart.disease.lm）

この関数は、線形モデルから取得した最も重要なパラメーターを次のようなテーブルに配置します。

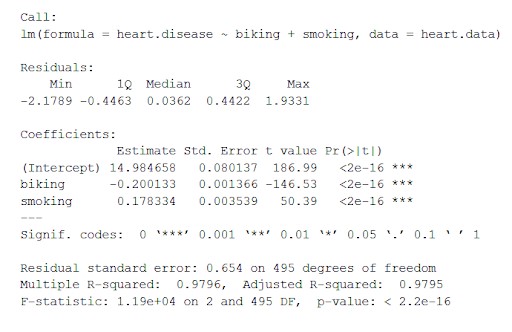
この表から、次のことが推測できます。

• 「呼び出し」の式、
• モデルの残差（「残差」）。 残差がほぼゼロを中心とし、両側に同様の広がりがある場合（中央値0.03、最小および最大-2および2）、モデルは不均一分散の仮定に適合します。
• モデルの回帰係数（「係数」）。

係数テーブルの行1（切片）：これは回帰方程式のy切片であり、回帰方程式をプラグインして従属変数値を予測するための推定切片を知るために使用されます。

心臓病=15+（-0.2 *自転車）+（0.178 *喫煙）±e

重回帰に関連するいくつかの用語

私。 推定列：これは推定された効果であり、回帰係数またはr2値とも呼ばれます。 推定によると、自転車で通勤する回数が1％増えるごとに、心臓病が0.2％減少し、喫煙が1％増えるごとに、心臓病が.17％増加します。

ii。 Std.error ：標準エラーを表示します 見積もりの​​。 これは、回帰係数の推定値の周りの変動を示す数値です。

iii。 t値：検定統計量を表示します。 これは、両側t検定からのt値です。

iv。 Pr（> | t |） ： t値の発生確率を示すのはp値です。

結果の報告

推定された効果、標準的な推定誤差、およびp値を含める必要があります。

上記の例では、自転車で通勤する頻度と心臓病との有意な関係と喫煙と心臓病の頻度はp<0.001であることがわかりました。

心臓病の頻度は、自転車に乗る回数が1％増えるごとに0.2％（または±0.0014）減少します。 心臓病の頻度は、喫煙が1％増加するごとに0.178％（または±0.0035）増加します。

調査結果のグラフィック表現

従属変数に対する複数の独立変数の影響をグラフで示すことができます。 この場合、x軸にプロットできる独立変数は1つだけです。

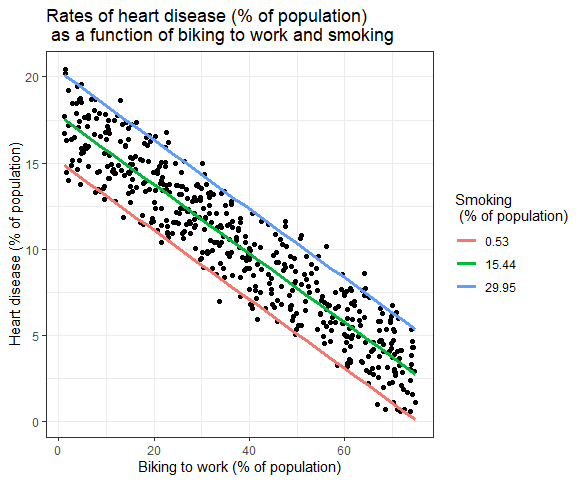
重回帰：グラフィック表現

ここでは、自転車で通勤する人の割合の観測値全体の従属変数（心臓病）の予測値がプロットされています。

独立変数に対する喫煙の影響については、喫煙を最小、平均、および最大の喫煙率で一定に保ちながら、予測値が計算されます。

また読む：線形回帰対。 ロジスティック回帰：線形回帰とロジスティック回帰の違い

最後の言葉

これで、このブログ投稿は終了です。 重回帰の概念と、予測分析を容易にするためにRの重回帰がどのように実装されているかを説明するために、最善を尽くしました。

データサイエンスの旅を支持し、キャリアを強化するためにRや他の多くの言語の概念をさらに学びたい場合は、 upGradに参加してください。 私たちは、データサイエンスの高度な認定プログラムを提供しています。これは、働く専門家向けに特別に設計されており、継続的なメンターシップによる300時間以上の学習が含まれています。