R'de Çoklu Doğrusal Regresyon [Grafikler ve Örneklerle]

Bir veri bilimcisi olarak, birçok projede sıklıkla tahmine dayalı analiz yapmanız istenir. Analiz, bağımlı bir değişken ile bir dizi bağımsız değişken arasında bir ilişki kurmaya yönelik istatistiksel bir yaklaşımdır. Bütün bu kavram, temel olarak iki tür olan bir doğrusal gerileme olarak adlandırılabilir: basit ve çoklu doğrusal gerileme.

R, veri bilimi ve analitik açısından en önemli dillerden biridir ve R'deki çoklu doğrusal regresyon değeri tutar. Tek bir yanıt değişkeninin Y'nin doğrusal olarak birden çok tahmin değişkenine bağlı olduğu senaryoyu açıklar.

Doğrusal Regresyon nedir?

arasındaki ilişkiyi göstermek veya tahmin etmek için doğrusal regresyon modelleri kullanılır. bağımlı ve bağımsız değişken. Regresyon analizinde kullanılan iki veya daha fazla bağımsız değişken olduğunda, model sadece doğrusal değil, çoklu bir regresyon modelidir.

Basit doğrusal regresyon, bir değişkenin değerini başka bir değişken kullanarak tahmin etmek için kullanılır. Düz bir çizgi, iki değişken arasındaki ilişkiyi doğrusal regresyon ile temsil eder.

Çoklu regresyonda bağımlı değişken ile iki veya daha fazla bağımsız değişken arasında doğrusal bir ilişki vardır. İlişki doğrusal olmayabilir ve bağımlı ve bağımsız değişkenler düz bir çizgi izlemeyecektir.

Çoklu doğrusal regresyon modeli tahminlerinin resimli gösterimi

Doğrusal ve doğrusal olmayan regresyon, iki veya daha fazla değişken kullanarak bir yanıtı izlemek için kullanılır. Doğrusal olmayan regresyon, deneme yanılma varsayımlarından oluşturulur ve yürütülmesi nispeten zordur.

Çoklu Doğrusal Regresyon Nedir?

Çoklu doğrusal regresyon, bir değişkenin sonucunu iki veya daha fazla değişkene dayalı olarak tahmin etmek için kullanılan istatistiksel bir analiz tekniğidir. Doğrusal regresyonun bir uzantısıdır ve çoklu regresyon olarak da bilinir. Tahmin edilecek değişken bağımlı değişkendir ve bağımlı değişkenin değerini tahmin etmek için kullanılan değişkenler bağımsız veya açıklayıcı değişkenler olarak bilinir.

Çoklu doğrusal regresyon, analistlerin modelin varyasyonunu ve her bağımsız değişkenin göreli katkısını belirlemesini sağlar. Çoklu regresyon, lineer ve lineer olmayan regresyon olmak üzere iki çeşittir.

Çoklu Regresyon Formülü

y değişkenini öngören üç tahmin değişkeni (x) ile çoklu regresyon aşağıdaki denklem olarak ifade edilir:

y = z0 + z1*x1 + z2*x2 + z3*x3

“z” değerleri regresyon ağırlıklarını temsil eder ve beta katsayılarıdır . Bunlar, tahmin edici değişken ile sonuç arasındaki ilişkidir.

• yi bağımlı veya tahmin edilen değişkendir
• z0 y kesme noktasıdır, yani x1 ve x2 0 olduğunda y'nin değeridir.
• z1 ve z2 , sırasıyla x1 ve x2'deki bir birimlik değişiklikle ilgili y'deki değişikliği temsil eden regresyon katsayılarıdır .

Çoklu Doğrusal Regresyon Varsayımları

Çoklu regresyon ve temel formülün özetini biliyoruz. Bununla birlikte, çoklu doğrusal regresyonun aşağıdaki gibi detaylandırıldığı bazı varsayımlar vardır:

i. Bağımlı ve Bağımsız Değişkenler Arasındaki İlişki

Bağımlı değişken, her bağımsız değişkenle doğrusal olarak ilişkilidir. Doğrusal ilişkileri kontrol etmek için bir dağılım grafiği oluşturulur ve doğrusallık için gözlenir. Dağılım grafiği ilişkisi doğrusal değilse, doğrusal olmayan bir regresyon gerçekleştirilir veya veriler istatistiksel yazılım kullanılarak aktarılır.

ii. Bağımsız Değişkenler Pek İlişkili Değil

Veriler, bağımsız değişkenlerin birbirleriyle yüksek düzeyde ilişkili olması durumunda meydana gelen çoklu bağlantı göstermemelidir. Bu, bağımlı değişkendeki varyansa katkıda bulunan belirli değişkenin ortaya çıkarılmasında sorunlar yaratacaktır.

iii. Artık Varyans Sabittir

Çoklu doğrusal regresyon, kalan değişkenlerin hatasının doğrusal modelin her noktasında benzer olduğunu varsayar. Bu homoskedastisite olarak bilinir. Veri analizi yapıldığında, noktaların bağımsız değişkenlerin değerleri arasında düzgün bir şekilde dağılıp dağılmadığını belirlemek için öngörülen değerlere karşı standart artıklar çizilir.

iv. Gözlem Bağımsızlığı

Gözlemler birbirinden olmalı ve artık değerler bağımsız olmalıdır. Durbin Watson istatistiği bunun için en iyi sonucu verir.

Yöntem, 0 ile 4 arasındaki değerleri gösterir, burada 0 ile 2 arasındaki bir değer pozitif otokorelasyonu gösterir ve 2 ile 4 arasındaki bir değer negatif otokorelasyonu gösterir. 2 değeri olan orta nokta, otokorelasyon olmadığını gösterir.

v. Çok Değişkenli Normallik

Çok değişkenli normallik, normal dağılmış artıklarla olur. Bu varsayım için artık değerlerinin nasıl dağıldığı gözlemlenir. İki yöntemle test edilebilir,

· Üst üste bindirilmiş normal eğriyi gösteren bir histogram ve

· Normal Olasılık Grafiği yöntemi.

Çoklu Doğrusal Regresyonun Uygulandığı Örnekler

Çoklu doğrusal regresyon, bir analistin bakış açısından çok önemli bir husustur. Konseptin uygulanabileceği bazı örnekler:

i. Bağımlı değişkenin değeri bağımsız değişkenlerle ilişkili olduğundan, belirli bir yağış, sıcaklık ve gübre seviyesinde bir mahsulün beklenen verimini tahmin etmek için çoklu regresyon kullanılır.

ii. Trendleri ve gelecekteki değerleri tahmin etmek için çoklu doğrusal regresyon analizi de kullanılır. Bu, özellikle altı ay sonraki altının fiyatını tahmin etmek için kullanışlıdır.

iii. Bir UBER sürücüsünün kat ettiği mesafe ile sürücünün yaşı ve sürücünün deneyim yılı sayısı arasındaki ilişkinin çıkarıldığı belirli bir örnekte. Bu regresyonda bağımlı değişken, UBER sürücüsü tarafından kapsanan mesafe. Bağımsız değişkenler, sürücünün yaşı ve sürüş deneyiminin yıl sayısıdır.

iv. Bir sınıfın genel not ortalaması ile çalıştıkları saat sayısı ve öğrencilerin boyları arasındaki ilişkiyi bulmak için çoklu regresyon analizinin kullanıldığı başka bir örnek. Bu regresyonda bağımlı değişken GNO, bağımsız değişkenler ise ders çalışma saatleri ve öğrencilerin boylarıdır.

v. Bir örgütteki bir grup çalışanın maaşı ile kaç yıl çalıştığı ve çalışanların yaşı arasındaki ilişki regresyon analizi ile belirlenebilir. Bu regresyonun bağımlı değişkeni maaş, bağımsız değişkenleri ise çalışanların deneyim ve yaşıdır.

Ayrıca Okuyun: Makine Öğreniminde Bilmeniz Gereken 6 Tip Regresyon Modeli

R'de Çoklu Doğrusal Regresyon

Çoklu doğrusal regresyonun yürütülebilmesinin birçok yolu vardır, ancak genellikle istatistiksel yazılım aracılığıyla yapılır. En çok kullanılan yazılımlardan biri, ücretsiz, güçlü ve kolayca bulunabilen R'dir. Önce R ile regresyonu gerçekleştirme adımlarını öğreneceğiz, ardından net bir anlayış örneği izleyeceğiz.

R'de Çoklu Regresyon Gerçekleştirme Adımları

1. Veri toplama: Tahminde kullanılacak veriler toplanır.
2. R'de Veri Yakalama: Kodu kullanarak verileri yakalama ve bir CSV dosyasını içe aktarma
3. R ile Veri Doğrusallığını Kontrol Etme: Bağımlı ve bağımsız değişken arasında doğrusal bir ilişki olduğundan emin olmak önemlidir. Dağılım grafikleri veya R'deki kod kullanılarak yapılabilir.
4. R'de Çoklu Doğrusal Regresyon Uygulaması: Bir dizi katsayı elde etmek için R'de çoklu doğrusal regresyon uygulamak için kod kullanma .
5. R ile Tahmin Yapmak: Sonunda tahmin edilen bir değer belirlenir.

R'de Çoklu Regresyon Uygulaması

Halk sağlığı araştırmacıları tarafından sigara içen, işe gidenler ve kalp hastalığı olan kişiler hakkında veri toplamak için belirli sayıda yerde bir anket yapıldığında R'nin nasıl uygulandığını anlayacağız.

R'de Çoklu Doğrusal Regresyon için Adım Adım Kılavuz:

i. Heart.data veri kümesini yükleyin ve aşağıdaki kodu çalıştırın

lm<-lm(kalp.hastalığı ~ bisiklet + sigara, veri = kalp.veri)

Veri seti kalbi. Veriler, 'lm()' (doğrusal model için denklem) kullanarak, bisiklete binme ve sigara içme bağımsız değişkenlerinin bağımlı değişken kalp hastalığı üzerindeki etkisini hesaplar.

ii. Sonuçları Yorumlama

modelin sonuçlarını görüntülemek için özet() işlevini kullanın:

özet(kalp.disease.lm)

Bu fonksiyon, lineer modelden elde edilen en önemli parametreleri aşağıdaki gibi görünen bir tabloya koyar:

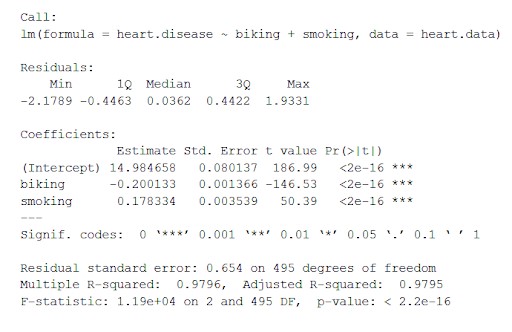
Bu tablodan şu sonucu çıkarabiliriz:

• 'Çağrı' formülü,
• Modelin artıkları ('Artıklar'). Artıklar kabaca sıfır etrafında ortalanmışsa ve her iki tarafta da benzer bir yayılımla (medyan 0,03 ve min ve maks -2 ve 2), model değişen varyans varsayımlarına uyar.
• Modelin regresyon katsayıları ('Katsayılar').

Katsayılar tablosunun 1. satırı (Kesme): Bu, regresyon denkleminin y-kesme noktasıdır ve regresyon denklemini takmak ve bağımlı değişken değerlerini tahmin etmek için tahmini kesmeyi bilmek için kullanılır.

kalp hastalığı = 15 + (-0.2*bisiklete binme) + (0,178*sigara içme) ± e

Çoklu Regresyonla İlgili Bazı Terimler

i. Tahmin Sütunu : Tahmin edilen etkidir ve regresyon katsayısı veya r2 değeri olarak da adlandırılır. Tahminler, işe giderken bisiklete binme oranındaki her yüzde birlik artışla ilişkili olarak kalp hastalığında yüzde 0,2'lik bir azalma olduğunu ve sigara içmedeki her yüzdelik artış için kalp hastalığında yüzde 0,17'lik bir artış olduğunu söylüyor.

ii. Std.error : Standart hatayı görüntüler tahminin. Bu, regresyon katsayısı tahminleri etrafındaki değişimi gösteren bir sayıdır.

iii. t Değer : Test istatistiğini gösterir . Bu, iki taraflı bir t-testinden elde edilen bir t -değeridir .

iv. Pr( > | t | ) : t - değerinin oluşma olasılığını gösteren p - değeridir.

Sonuçları Raporlama

Tahmini etkiyi, standart tahmin hatasını ve p - değerini dahil etmeliyiz.

Yukarıdaki örnekte işe bisikletle gitme sıklığı ile kalp hastalığı sıklığı ile sigara içme ve kalp hastalığı sıklığı arasındaki anlamlı ilişkiler p < 0,001 olarak bulunmuştur.

Bisiklete binmede her %1'lik artış için kalp hastalığı sıklığı %0,2 (veya ± 0,0014) azalır. Sigaradaki her %1'lik artış için kalp hastalığı sıklığı %0.178 (veya ± 0.0035) artar.

Bulguların Grafik Gösterimi

Birden çok bağımsız değişkenin bağımlı değişken üzerindeki etkileri bir grafikte gösterilebilir. Bunda, x ekseninde yalnızca bir bağımsız değişken çizilebilir.

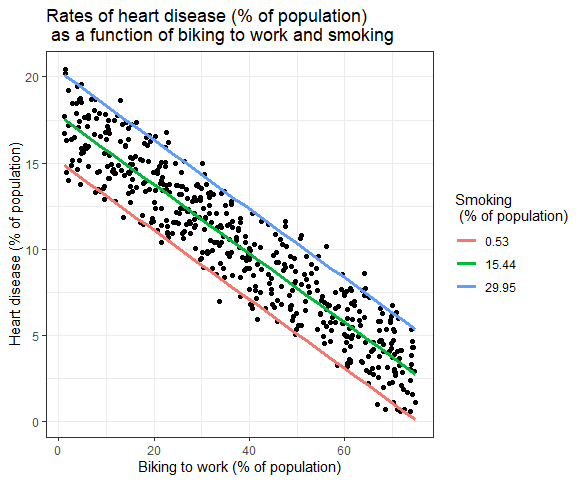
Çoklu Doğrusal Regresyon: Grafik Gösterim

Burada, işe bisikletle giden insanların yüzdesi için gözlemlenen değerler boyunca bağımlı değişkenin (kalp hastalığı) tahmin edilen değerleri çizilir.

Sigara içmenin bağımsız değişken üzerindeki etkisi için, sigara içmenin minimum, ortalama ve maksimum sigara içme oranlarında sabit tutularak öngörülen değerler hesaplanmıştır.

Ayrıca Okuyun: Doğrusal Regresyon Vs. Lojistik Regresyon: Doğrusal Regresyon ve Lojistik Regresyon Arasındaki Fark

Son sözler

Bu, bu blog gönderisinin sonunu işaret ediyor. Tahmin analizini kolaylaştırmak için size çoklu doğrusal regresyon kavramını ve R'deki çoklu regresyonun nasıl uygulandığını açıklamak için elimizden gelenin en iyisini yapmaya çalıştık.

Veri bilimi yolculuğunuzu desteklemek ve kariyerinizi güçlendirmek için R ve diğer birçok dilde daha fazla kavram öğrenmek istiyorsanız upGrad'a katılın . Çalışan profesyoneller için özel olarak tasarlanmış ve sürekli mentorluk ile 300+ saatlik öğrenmeyi içeren Veri Biliminde Gelişmiş Sertifikasyon Programını sunuyoruz .