การถดถอยเชิงเส้นพหุคูณใน R [ด้วยกราฟและตัวอย่าง]

ในฐานะนักวิทยาศาสตร์ข้อมูล คุณมักถูกขอให้ทำการวิเคราะห์เชิงคาดการณ์ในหลายโครงการ การวิเคราะห์เป็นวิธีทางสถิติสำหรับการสร้างความสัมพันธ์ระหว่างตัวแปรตามกับชุดของตัวแปรอิสระ แนวคิดทั้งหมดนี้สามารถเรียกได้ว่าเป็นการถดถอยเชิงเส้น ซึ่งโดยพื้นฐานแล้วมีสองประเภท: การถดถอยเชิงเส้นแบบง่ายและพหุคูณ

R เป็นหนึ่งในภาษาที่สำคัญที่สุดในแง่ของวิทยาศาสตร์ข้อมูลและการวิเคราะห์ และการ ถดถอยเชิงเส้นพหุคูณใน R ก็มีค่าเช่นกัน มันอธิบายสถานการณ์สมมติที่ตัวแปรตอบสนองเดียว Y ขึ้นอยู่กับตัวแปรทำนายหลายตัวเชิงเส้น

การถดถอยเชิงเส้นคืออะไร?

ตัวแบบการถดถอยเชิงเส้นใช้เพื่อแสดงหรือทำนายความสัมพันธ์ระหว่าง a ตัวแปรตามและตัวแปรอิสระ เมื่อมีตัวแปรอิสระตั้งแต่สองตัวขึ้นไปที่ใช้ในการวิเคราะห์การถดถอย ตัวแบบจะไม่ใช่แค่เชิงเส้น แต่เป็นแบบจำลองการถดถอยพหุคูณ

การถดถอยเชิงเส้นอย่างง่ายใช้สำหรับการทำนายค่าของตัวแปรหนึ่งโดยใช้ตัวแปรอื่น เส้นตรงแสดงถึงความสัมพันธ์ระหว่างตัวแปรสองตัวที่มีการถดถอยเชิงเส้น

มีความสัมพันธ์เชิงเส้นตรงระหว่างตัวแปรตามที่มีตัวแปรอิสระตั้งแต่สองตัวขึ้นไปในการถดถอยพหุคูณ ความสัมพันธ์สามารถไม่เป็นเชิงเส้นได้ และตัวแปรตามและตัวแปรอิสระจะไม่เป็นไปตามเส้นตรง

การแสดงภาพของการทำนายแบบจำลองการถดถอยเชิงเส้นพหุคูณ

การถดถอยเชิงเส้นและไม่เชิงเส้นใช้เพื่อติดตามการตอบสนองโดยใช้ตัวแปรตั้งแต่สองตัวขึ้นไป การถดถอยแบบไม่เชิงเส้นถูกสร้างขึ้นจากสมมติฐานจากการลองผิดลองถูก และค่อนข้างยากที่จะดำเนินการ

การถดถอยเชิงเส้นพหุคูณคืออะไร?

การถดถอยเชิงเส้นพหุคูณเป็นเทคนิคการวิเคราะห์ทางสถิติที่ใช้ในการทำนายผลลัพธ์ของตัวแปรโดยพิจารณาจากตัวแปรตั้งแต่สองตัวขึ้นไป มันเป็นส่วนขยายของการถดถอยเชิงเส้นและเรียกอีกอย่างว่าการถดถอยพหุคูณ ตัวแปรที่จะทำนายคือตัวแปรตาม และตัวแปรที่ใช้ในการทำนายค่าของตัวแปรตามนั้นเรียกว่าตัวแปรอิสระหรือตัวแปรอธิบาย

การถดถอยเชิงเส้นพหุคูณช่วยให้นักวิเคราะห์สามารถกำหนดความผันแปรของแบบจำลองและการมีส่วนร่วมเชิงสัมพันธ์ของตัวแปรอิสระแต่ละตัวได้ การถดถอยพหุคูณมีสองประเภทคือการถดถอยเชิงเส้นและไม่เชิงเส้น

สูตรถดถอยพหุคูณ

การถดถอยพหุคูณที่มีสามตัวแปรทำนาย (x) ตัวแปรทำนาย y แสดงเป็นสมการต่อไปนี้:

y = z0 + z1*x1 + z2*x2 + z3*x3

ค่า "z" แสดงถึงน้ำหนักการถดถอย และเป็น ค่า สัมประสิทธิ์เบตา เป็นความสัมพันธ์ระหว่างตัวแปรทำนายและผลลัพธ์

• yi เป็นตัวแปรตามหรือทำนายไว้
• z0 คือค่าตัดแกน y เช่น ค่าของ y เมื่อ x1 และ x2 เป็น 0
• z1 และ z2 เป็นสัมประสิทธิ์การถดถอยที่แสดงถึงการเปลี่ยนแปลงใน y ที่เกี่ยวข้องกับการเปลี่ยนแปลงหนึ่งหน่วยใน x1 และ x2 ตามลำดับ

สมมติฐานของการถดถอยเชิงเส้นพหุคูณ

เรารู้บทสรุปเกี่ยวกับการถดถอยพหุคูณและสูตรพื้นฐานแล้ว อย่างไรก็ตาม มีสมมติฐานบางประการที่การถดถอยเชิงเส้นพหุคูณมีรายละเอียดดังนี้:

ฉัน. ความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระ

ตัวแปรตามสัมพันธ์เชิงเส้นกับตัวแปรอิสระแต่ละตัว ในการตรวจสอบความสัมพันธ์เชิงเส้น มีการสร้าง scatterplot และสังเกตความเป็นเชิงเส้น ถ้าความสัมพันธ์ scatterplot ไม่เป็นเชิงเส้น แสดงว่ามีการถดถอยแบบไม่เชิงเส้น หรือข้อมูลถูกถ่ายโอนโดยใช้ซอฟต์แวร์ทางสถิติ

ii ตัวแปรอิสระไม่มีความสัมพันธ์กันมากนัก

ข้อมูลไม่ควรแสดง multicollinearity ซึ่งเกิดขึ้นในกรณีที่ตัวแปรอิสระมีความสัมพันธ์กันสูง สิ่งนี้จะสร้างปัญหาในการดึงข้อมูลตัวแปรเฉพาะที่ทำให้เกิดความแปรปรวนในตัวแปรตาม

สาม. ความแปรปรวนคงเหลือคงที่

การถดถอยเชิงเส้นพหุคูณถือว่าข้อผิดพลาดของตัวแปรที่เหลือจะคล้ายกันในแต่ละจุดของโมเดลเชิงเส้น สิ่งนี้เรียกว่า homoscedasticity เมื่อการวิเคราะห์ข้อมูลเสร็จสิ้น ค่าคงเหลือมาตรฐานเทียบกับค่าที่คาดการณ์ไว้จะถูกวางแผนเพื่อพิจารณาว่าจุดต่างๆ มีการกระจายอย่างเหมาะสมในค่าของตัวแปรอิสระหรือไม่

iv การสังเกตการณ์อิสระ

การสังเกตควรเป็นของกันและกัน และค่าคงเหลือควรเป็นอิสระ สถิติ Durbin Watson ทำงานได้ดีที่สุดสำหรับสิ่งนี้

วิธีการนี้แสดงค่าตั้งแต่ 0 ถึง 4 โดยที่ค่าระหว่าง 0 ถึง 2 แสดงความสัมพันธ์อัตโนมัติเชิงบวก และจาก 2 ถึง 4 แสดงความสัมพันธ์อัตโนมัติเชิงลบ จุดกึ่งกลาง ค่า 2 แสดงว่าไม่มีความสัมพันธ์อัตโนมัติ

v. ความปกติหลายตัวแปร

ภาวะปกติหลายตัวแปรเกิดขึ้นกับเศษที่เหลือแบบกระจายตามปกติ สำหรับสมมติฐานนี้ จะสังเกตได้ว่ามีการกระจายค่าของส่วนที่เหลืออย่างไร สามารถทดสอบได้ 2 วิธี คือ

· ฮิสโตแกรมที่แสดงเส้นโค้งปกติที่ซ้อนทับและ

· วิธีการแปลงความน่าจะเป็นปกติ

กรณีที่มีการใช้การถดถอยเชิงเส้นพหุคูณ

การถดถอยเชิงเส้นพหุคูณเป็นสิ่งสำคัญมากจากมุมมองของนักวิเคราะห์ นี่คือตัวอย่างบางส่วนที่สามารถประยุกต์ใช้แนวคิดนี้ได้:

ฉัน. เนื่องจากค่าของตัวแปรตามมีความสัมพันธ์กับตัวแปรอิสระ จึงใช้การถดถอยพหุคูณเพื่อคาดการณ์ผลผลิตที่คาดว่าจะได้รับจากปริมาณน้ำฝน อุณหภูมิ และระดับปุ๋ย

ii การวิเคราะห์การถดถอยเชิงเส้นพหุคูณยังใช้เพื่อทำนายแนวโน้มและค่าในอนาคตอีกด้วย สิ่งนี้มีประโยชน์อย่างยิ่งในการทำนายราคาทองคำในช่วงหกเดือนต่อจากนี้

สาม. ในตัวอย่างเฉพาะที่ความสัมพันธ์ระหว่างระยะทางที่ครอบคลุมโดยคนขับ UBER กับอายุของคนขับและจำนวนปีของประสบการณ์ของคนขับนั้นถูกลบออกไป ในการถดถอยนี้ ตัวแปรตามคือ ระยะทางที่ครอบคลุมโดยคนขับ UBER ตัวแปรอิสระคืออายุของผู้ขับขี่และจำนวนปีของประสบการณ์ในการขับขี่

iv อีกตัวอย่างหนึ่งที่ใช้การวิเคราะห์การถดถอยพหุคูณในการหาความสัมพันธ์ระหว่างเกรดเฉลี่ยของชั้นเรียนของนักเรียนกับจำนวนชั่วโมงที่พวกเขาเรียนและความสูงของนักเรียน ตัวแปรตามในการถดถอยนี้คือ GPA และตัวแปรอิสระคือจำนวนชั่วโมงเรียนและความสูงของนักเรียน

v. ความสัมพันธ์ระหว่างเงินเดือนของกลุ่มพนักงานในองค์กรกับจำนวนปีของการขยายงานอายุของพนักงานสามารถกำหนดได้ด้วยการวิเคราะห์การถดถอย ตัวแปรตามสำหรับการถดถอยนี้คือเงินเดือน และตัวแปรอิสระคือประสบการณ์และอายุของพนักงาน

อ่านเพิ่มเติม: 6 ประเภทของแบบจำลองการถดถอยในการเรียนรู้ของเครื่องที่คุณควรรู้

การถดถอยเชิงเส้นพหุคูณใน R

มีหลายวิธีที่สามารถดำเนินการถดถอยเชิงเส้นหลายแบบได้ แต่โดยทั่วไปจะทำผ่านซอฟต์แวร์ทางสถิติ หนึ่งในซอฟต์แวร์ที่ใช้กันมากที่สุดคือ R ซึ่งฟรี ทรงพลัง และใช้งานได้ง่าย ก่อนอื่นเราจะเรียนรู้ขั้นตอนในการถดถอยด้วย R ตามด้วยตัวอย่างความเข้าใจที่ชัดเจน

ขั้นตอนในการถดถอยพหุคูณใน R

1. การเก็บรวบรวมข้อมูล: ข้อมูลที่จะใช้ในการทำนายจะถูกรวบรวม
2. Data Capturing in R: ดักจับข้อมูลโดยใช้โค้ดและนำเข้าไฟล์ CSV
3. การตรวจสอบความเป็นเส้นตรงของข้อมูลด้วย R: สิ่งสำคัญคือต้องแน่ใจว่ามีความสัมพันธ์เชิงเส้นระหว่างตัวแปรตามและตัวแปรอิสระ สามารถทำได้โดยใช้แปลงกระจายหรือรหัสในR
4. การใช้การถดถอยเชิงเส้นพหุคูณใน R: การใช้รหัสเพื่อใช้ การถดถอยเชิงเส้นพหุคูณใน R เพื่อให้ได้ชุดของสัมประสิทธิ์
5. การทำนายด้วย R: ค่าที่คาดการณ์ไว้จะถูกกำหนดในตอนท้าย

การดำเนินการถดถอยพหุคูณในR

เราจะเข้าใจวิธีการใช้ R เมื่อทำการสำรวจในสถานที่จำนวนหนึ่งโดยนักวิจัยด้านสาธารณสุขเพื่อรวบรวมข้อมูลเกี่ยวกับประชากรที่สูบบุหรี่ ผู้ที่เดินทางไปทำงาน และผู้ที่เป็นโรคหัวใจ

คำแนะนำทีละขั้นตอนสำหรับการถดถอยเชิงเส้นพหุคูณใน R:

ฉัน. โหลดชุดข้อมูล heart.data แล้วรันโค้ดต่อไปนี้

lm<-lm(heart.disease ~ ปั่นจักรยาน + สูบบุหรี่ data = heart.data)

ชุดข้อมูลหัวใจ ข้อมูลจะคำนวณผลกระทบของตัวแปรอิสระในการขี่จักรยานและการสูบบุหรี่ต่อโรคหัวใจผันแปรตามตัวแปรตามโดยใช้ 'lm()' (สมการสำหรับแบบจำลองเชิงเส้น)

ii การตีความผลลัพธ์

ใช้ฟังก์ชันสรุป () เพื่อดูผลลัพธ์ของโมเดล:

สรุป (heart.disease.lm)

ฟังก์ชันนี้ใส่พารามิเตอร์ที่สำคัญที่สุดที่ได้รับจากตัวแบบเชิงเส้นลงในตารางที่มีลักษณะดังนี้:

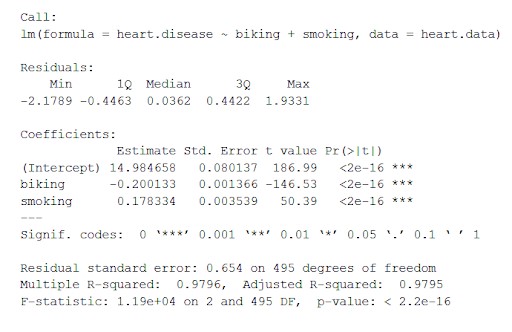
จากตารางนี้เราสามารถอนุมานได้:

• สูตรของ 'โทร'
• เศษของแบบจำลอง ('เศษ') หากเศษเหลืออยู่ตรงกลางประมาณศูนย์และมีการแพร่กระจายที่คล้ายกันทั้งสองด้าน (มัธยฐาน 0.03 และต่ำสุดและสูงสุด -2 และ 2) แบบจำลองจะพอดีกับสมมติฐานที่แตกต่างกัน
• สัมประสิทธิ์การถดถอยของแบบจำลอง ('สัมประสิทธิ์')

แถวที่ 1 ของตารางสัมประสิทธิ์ (Intercept): นี่คือจุดตัดแกน y ของสมการถดถอยและใช้เพื่อทราบค่าตัดขวางโดยประมาณเพื่อแทนสมการการถดถอยและทำนายค่าตัวแปรตาม

โรคหัวใจ = 15 + (-0.2*ปั่นจักรยาน) + (0.178*สูบบุหรี่) ± e

คำบางคำที่เกี่ยวข้องกับการถดถอยพหุคูณ

ฉัน. คอลัมน์ประมาณการ : เป็นผลกระทบโดยประมาณและเรียกอีกอย่างว่าค่าสัมประสิทธิ์การถดถอยหรือค่า r2 การประมาณการบอกว่าทุกๆ หนึ่งเปอร์เซ็นต์ในการขี่จักรยานไปทำงาน โรคหัวใจจะลดลง 0.2 เปอร์เซ็นต์ และการสูบบุหรี่ที่เพิ่มขึ้นทุกๆ เปอร์เซ็นต์ โรคหัวใจจะเพิ่มขึ้น .17 เปอร์เซ็นต์

ii Std.error : แสดงข้อผิดพลาดมาตรฐาน ของการประมาณการ นี่คือตัวเลขที่แสดงความผันแปรรอบค่าประมาณของสัมประสิทธิ์การถดถอย

สาม. t Value : แสดง สถิติการ ทดสอบ เป็น ค่า t จาก การทดสอบ t แบบสอง ด้าน

iv Pr( > | t | ) : เป็น ค่า p ซึ่งแสดงความน่าจะเป็นของการเกิด t -value

การรายงานผล

เราควรรวมผลกระทบโดยประมาณ ข้อผิดพลาดในการประมาณมาตรฐาน และ ค่า p

จากตัวอย่างข้างต้น พบว่าความสัมพันธ์ที่มีนัยสำคัญระหว่างความถี่ของการปั่นจักรยานไปทำงานกับโรคหัวใจ กับความถี่ของการสูบบุหรี่และโรคหัวใจ มีค่า p < 0.001

ความถี่ของโรคหัวใจลดลง 0.2% (หรือ ± 0.0014) ทุกครั้งที่ปั่นจักรยานเพิ่มขึ้น 1% ความถี่ของโรคหัวใจเพิ่มขึ้น 0.178% (หรือ ± 0.0035) ทุกๆ 1% ของการสูบบุหรี่

การแสดงกราฟิกของผลการวิจัย

ผลกระทบของตัวแปรอิสระหลายตัวต่อตัวแปรตามสามารถแสดงในกราฟได้ ในกรณีนี้ สามารถพล็อตตัวแปรอิสระได้เพียงตัวเดียวบนแกน x

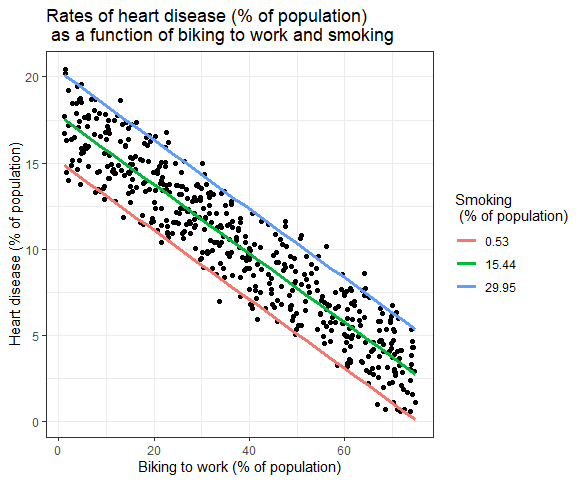
การถดถอยเชิงเส้นพหุคูณ: การแทนแบบกราฟิก

ในที่นี้ ค่าที่คาดการณ์ไว้ของตัวแปรตาม (โรคหัวใจ) จากค่าที่สังเกตได้สำหรับเปอร์เซ็นต์ของผู้ที่ขี่จักรยานไปทำงานนั้นถูกวางแผนไว้

สำหรับผลกระทบของการสูบบุหรี่ต่อตัวแปรอิสระ ค่าที่คาดการณ์ไว้จะถูกคำนวณ โดยคงค่าคงที่การสูบบุหรี่ไว้ที่อัตราการสูบบุหรี่ต่ำสุด ค่าเฉลี่ย และสูงสุด

อ่านเพิ่มเติม: การถดถอยเชิงเส้น Vs Logistic Regression: ความแตกต่างระหว่างการถดถอยเชิงเส้นและการถดถอยโลจิสติก

คำพูดสุดท้าย

นี่เป็นจุดสิ้นสุดของโพสต์บล็อกนี้ เราได้พยายามอย่างเต็มที่เพื่ออธิบายให้คุณทราบถึงแนวคิดของการถดถอยเชิงเส้นพหุคูณและวิธีนำการถดถอยพหุคูณใน R มาใช้เพื่อทำให้การวิเคราะห์การทำนายง่ายขึ้น

หากคุณมีความกระตือรือร้นที่จะสนับสนุนเส้นทางวิทยาศาสตร์ข้อมูลของคุณและเรียนรู้แนวคิดเพิ่มเติมเกี่ยวกับ R และภาษาอื่นๆ อีกมากมายเพื่อเสริมสร้างอาชีพการงานของคุณ เข้า ร่วม upGrad เราขอเสนอ โปรแกรมการรับรองขั้นสูงใน Data Science ซึ่งออกแบบมาเป็นพิเศษสำหรับมืออาชีพด้านการทำงานและรวมถึงการเรียนรู้มากกว่า 300 ชั่วโมงพร้อมการให้คำปรึกษาอย่างต่อเนื่อง