Régression linéaire multiple dans R [avec graphiques et exemples]

En tant que data scientist, vous êtes fréquemment sollicité pour effectuer des analyses prédictives dans de nombreux projets. Une analyse est une approche statistique permettant d'établir une relation entre une variable dépendante et un ensemble de variables indépendantes. Tout ce concept peut être qualifié de régression linéaire, qui est essentiellement de deux types : régression linéaire simple et multiple.

R est l'un des langages les plus importants en termes de science des données et d'analyse, tout comme la régression linéaire multiple dans R a de la valeur. Il décrit le scénario dans lequel une seule variable de réponse Y dépend linéairement de plusieurs variables prédictives.

Qu'est-ce qu'une régression linéaire ?

Les modèles de régression linéaire sont utilisés pour montrer ou prédire la relation entre un variable dépendante et une variable indépendante. Lorsqu'il y a deux ou plusieurs variables indépendantes utilisées dans l'analyse de régression, le modèle n'est pas simplement linéaire mais un modèle de régression multiple.

La régression linéaire simple est utilisée pour prédire la valeur d'une variable en utilisant une autre variable. Une ligne droite représente la relation entre les deux variables avec une régression linéaire.

Il existe une relation linéaire entre une variable dépendante et deux variables indépendantes ou plus dans la régression multiple. La relation peut également être non linéaire et les variables dépendantes et indépendantes ne suivront pas une ligne droite.

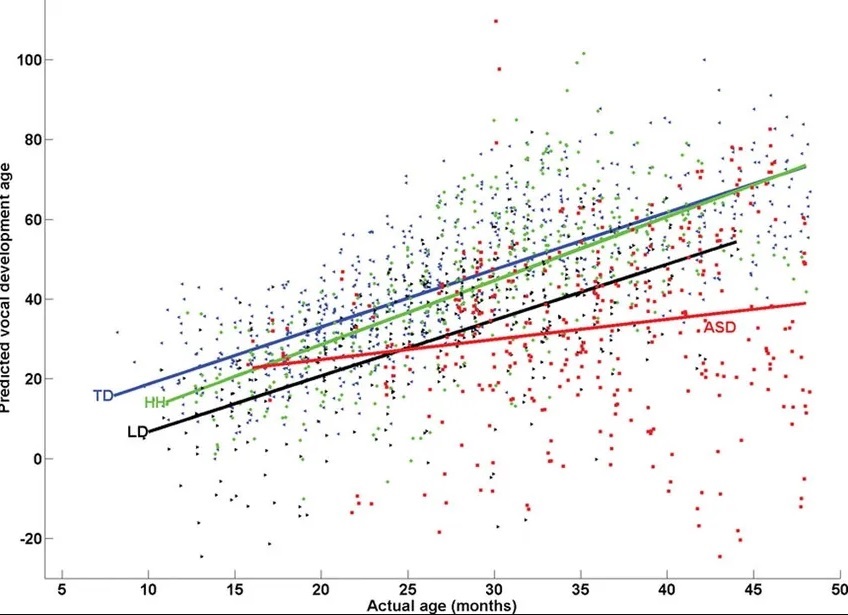
Représentation graphique des prédictions du modèle de régression linéaire multiple

La régression linéaire et non linéaire est utilisée pour suivre une réponse à l'aide de deux variables ou plus. La régression non linéaire est créée à partir d'hypothèses d'essais et d'erreurs et est relativement difficile à exécuter.

Qu'est-ce que la régression linéaire multiple ?

La régression linéaire multiple est une technique d'analyse statistique utilisée pour prédire le résultat d'une variable en fonction de deux variables ou plus. C'est une extension de la régression linéaire et également connue sous le nom de régression multiple. La variable à prédire est la variable dépendante, et les variables utilisées pour prédire la valeur de la variable dépendante sont appelées variables indépendantes ou explicatives.

La régression linéaire multiple permet aux analystes de déterminer la variation du modèle et la contribution relative de chaque variable indépendante. La régression multiple est de deux types, la régression linéaire et la régression non linéaire.

Formule de régression multiple

La régression multiple avec trois variables prédictives (x) prédisant la variable y est exprimée par l'équation suivante :

y = z0 + z1*x1 + z2*x2 + z3*x3

Les valeurs « z » représentent les poids de régression et sont les coefficients bêta . Ils sont l'association entre la variable prédictive et le résultat.

• yi est une variable dépendante ou prédite
• z0 est l'ordonnée à l'origine, c'est-à-dire la valeur de y lorsque x1 et x2 sont 0
• z1 et z2 sont les coefficients de régression représentant le changement de y lié à un changement d'une unité de x1 et x2 , respectivement.

Hypothèses de la régression linéaire multiple

Nous avons connu le mémoire sur la régression multiple et la formule de base. Cependant, il existe certaines hypothèses sur lesquelles la régression linéaire multiple est basée, détaillées ci-dessous :

je. Relation entre les variables dépendantes et indépendantes

La variable dépendante est liée linéairement à chaque variable indépendante. Pour vérifier les relations linéaires, un nuage de points est créé et est observé pour la linéarité. Si la relation du nuage de points n'est pas linéaire, une régression non linéaire est effectuée ou les données sont transférées à l'aide d'un logiciel statistique.

ii. Les variables indépendantes ne sont pas très corrélées

Les données ne doivent pas afficher de multicolinéarité, ce qui se produit lorsque les variables indépendantes sont fortement corrélées les unes aux autres. Cela créera des problèmes pour extraire la variable spécifique contribuant à la variance de la variable dépendante.

iii. La variance résiduelle est constante

La régression linéaire multiple suppose que l'erreur des variables restantes est similaire à chaque point du modèle linéaire. C'est ce qu'on appelle l'homoscédasticité. Lorsque l'analyse des données est terminée, les résidus standard par rapport aux valeurs prédites sont tracés pour déterminer si les points sont correctement répartis entre les valeurs des variables indépendantes.

iv. Indépendance des observations

Les observations doivent être les unes des autres et les valeurs résiduelles doivent être indépendantes. La statistique de Durbin Watson fonctionne le mieux pour cela.

La méthode affiche des valeurs de 0 à 4, où une valeur entre 0 et 2 indique une autocorrélation positive, et de 2 à 4 indique une autocorrélation négative. Le point médian, une valeur de 2, indique qu'il n'y a pas d'autocorrélation.

v. Normalité multivariée

La normalité multivariée se produit avec des résidus normalement distribués. Pour cette hypothèse, on observe comment les valeurs des résidus sont distribuées. Il peut être testé selon deux méthodes,

· Un histogramme montrant une courbe normale superposée et

· La méthode du tracé de probabilité normale.

Instances où la régression linéaire multiple est appliquée

La régression linéaire multiple est un aspect très important du point de vue d'un analyste. Voici quelques exemples où le concept peut être applicable :

je. Comme la valeur de la variable dépendante est corrélée aux variables indépendantes, la régression multiple est utilisée pour prédire le rendement attendu d'une culture à certaines précipitations, températures et niveaux d'engrais.

ii. L'analyse de régression linéaire multiple est également utilisée pour prédire les tendances et les valeurs futures. Ceci est particulièrement utile pour prédire le prix de l'or dans les six mois à venir.

iii. Dans un exemple particulier où la relation entre la distance parcourue par un conducteur UBER et l'âge du conducteur et le nombre d'années d'expérience du conducteur est retirée. Dans cette régression, la variable dépendante est le distance parcourue par le chauffeur UBER. Les variables indépendantes sont l'âge du conducteur et le nombre d'années d'expérience dans la conduite.

iv. Un autre exemple où l'analyse de régressions multiples est utilisée pour trouver la relation entre le GPA d'une classe d'étudiants et le nombre d'heures qu'ils étudient et la taille des étudiants. La variable dépendante dans cette régression est le GPA, et les variables indépendantes sont le nombre d'heures d'étude et la taille des étudiants.

v. La relation entre le salaire d'un groupe d'employés dans une organisation et le nombre d'années d'ancienneté de l'organisation et l'âge des employés peut être déterminée par une analyse de régression. La variable dépendante de cette régression est le salaire, et les variables indépendantes sont l'expérience et l'âge des employés.

Lisez aussi : 6 types de modèles de régression dans l'apprentissage automatique que vous devriez connaître

Régression linéaire multiple dans R

Il existe de nombreuses façons d'exécuter la régression linéaire multiple, mais elle est généralement effectuée via un logiciel statistique. L'un des logiciels les plus utilisés est R qui est gratuit, puissant et facilement disponible. Nous allons d'abord apprendre les étapes pour effectuer la régression avec R, suivi d'un exemple de compréhension claire.

Étapes pour effectuer une régression multiple dans R

1. Collecte de données: Les données à utiliser dans la prédiction sont collectées.
2. Capture de données dans R : Capture des données à l'aide du code et importation d'un fichier CSV
3. Vérification de la linéarité des données avec R : Il est important de s'assurer qu'il existe une relation linéaire entre la variable dépendante et la variable indépendante. Cela peut être fait en utilisant des nuages ​​de points ou le code en R
4. Application de la régression linéaire multiple dans R : Utilisation du code pour appliquer une régression linéaire multiple dans R pour obtenir un ensemble de coefficients.
5. Faire des prédictions avec R : Une valeur prédite est déterminée à la fin.

Implémentation de la régression multiple dans R

On comprendra comment R est mis en œuvre lorsqu'une enquête est menée dans un certain nombre d'endroits par les chercheurs en santé publique pour recueillir les données sur la population qui fume, qui se rend au travail et les personnes atteintes d'une maladie cardiaque.

Guide pas à pas pour la régression linéaire multiple dans R :

je. Chargez le jeu de données heart.data et exécutez le code suivant

lm<-lm(heart.disease ~ vélo + tabagisme, data = heart.data)

Le cœur de l'ensemble de données. Les données calculent l'effet des variables indépendantes vélo et tabagisme sur la variable dépendante cardiopathie à l'aide de « lm() » (l'équation du modèle linéaire).

ii. Interprétation des résultats

utilisez la fonction summary() pour afficher les résultats du modèle :

résumé(heart.disease.lm)

Cette fonction place les paramètres les plus importants obtenus à partir du modèle linéaire dans un tableau qui se présente comme ci-dessous :

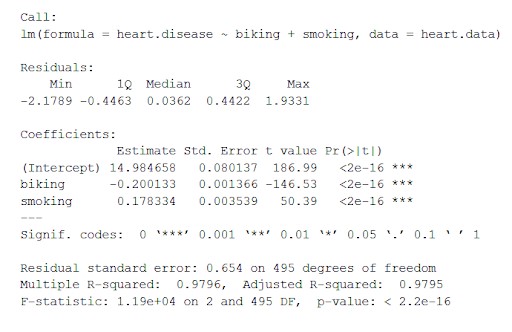
De ce tableau nous pouvons déduire :

• La formule de 'Call',
• Les résidus du modèle ('Residuals'). Si les résidus sont à peu près centrés autour de zéro et avec une dispersion similaire de chaque côté (médiane 0,03, et min et max -2 et 2), alors le modèle correspond aux hypothèses d'hétéroscédasticité.
• Les coefficients de régression du modèle ('Coefficients').

Ligne 1 du tableau des coefficients (interception) : il s'agit de l'ordonnée à l'origine de l'équation de régression et utilisée pour connaître l'interception estimée pour brancher l'équation de régression et prédire les valeurs de la variable dépendante.

maladie cardiaque = 15 + (-0,2*vélo) + (0,178*tabagisme) ± e

Quelques termes liés à la régression multiple

je. Colonne d'estimation : Il s'agit de l'effet estimé et est également appelé coefficient de régression ou valeur r2. Les estimations indiquent que pour chaque pour cent d'augmentation du vélo pour se rendre au travail, il y a une diminution associée de 0,2 pour cent des maladies cardiaques, et pour chaque pour cent d'augmentation du tabagisme, il y a une augmentation de 0,17 pour cent des maladies cardiaques.

ii. Std.error : Il affiche l'erreur standard de l'estimation. Il s'agit d'un nombre qui montre une variation autour des estimations du coefficient de régression.

iii. t Valeur : Affiche la statistique du test . Il s'agit d'une valeur t issue d'un test t bilatéral .

iv. Pr( > | t | ) : C'est la valeur p qui indique la probabilité d'occurrence de la valeur t .

Rapporter les résultats

Nous devrions inclure l'effet estimé, l'erreur d'estimation standard et la valeur de p .

Dans l'exemple ci-dessus, les relations significatives entre la fréquence du vélo pour se rendre au travail et les maladies cardiaques et la fréquence du tabagisme et des maladies cardiaques se sont avérées être p < 0,001.

La fréquence des maladies cardiaques diminue de 0,2 % (ou ± 0,0014) pour chaque augmentation de 1 % de la pratique du vélo. La fréquence des maladies cardiaques augmente de 0,178 % (ou ± 0,0035) pour chaque augmentation de 1 % du tabagisme.

Représentation graphique des résultats

Les effets de plusieurs variables indépendantes sur la variable dépendante peuvent être représentés dans un graphique. En cela, une seule variable indépendante peut être tracée sur l'axe des x.

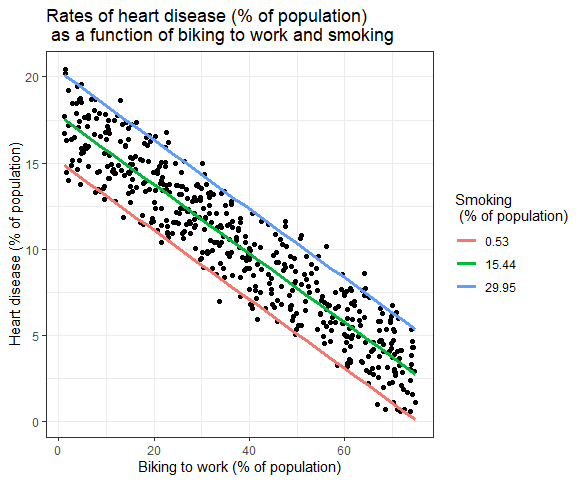
Régression linéaire multiple : représentation graphique

Ici, les valeurs prédites de la variable dépendante (maladie cardiaque) à travers les valeurs observées pour le pourcentage de personnes se rendant au travail à vélo sont tracées.

Pour l'effet du tabagisme sur la variable indépendante, les valeurs prédites sont calculées, en maintenant le tabagisme constant aux taux de tabagisme minimum, moyen et maximum.

Lisez aussi: Régression linéaire Vs. Régression logistique : différence entre la régression linéaire et la régression logistique

Derniers mots

Ceci marque la fin de cet article de blog. Nous avons fait de notre mieux pour vous expliquer le concept de régression linéaire multiple et comment la régression multiple dans R est implémentée pour faciliter l'analyse de prédiction.

Si vous souhaitez approuver votre parcours en science des données et apprendre davantage de concepts de R et de nombreux autres langages pour renforcer votre carrière, rejoignez upGrad . Nous proposons le programme de certification avancée en science des données, spécialement conçu pour les professionnels en activité et comprenant plus de 300 heures d'apprentissage avec un mentorat continu.