الانحدار الخطي المتعدد في R [مع الرسوم البيانية والأمثلة]

بصفتك عالم بيانات ، يُطلب منك كثيرًا إجراء تحليل تنبؤي في العديد من المشاريع. التحليل هو نهج إحصائي لتأسيس علاقة بين متغير تابع بمجموعة من المتغيرات المستقلة. يمكن وصف هذا المفهوم بأكمله بأنه الانحدار الخطي ، والذي يتكون أساسًا من نوعين: الانحدار الخطي البسيط والمتعدد.

R هي واحدة من أهم اللغات من حيث علم البيانات والتحليلات ، وكذلك الانحدار الخطي المتعدد في R يحمل قيمة. يصف السيناريو حيث يعتمد متغير استجابة واحد Y بشكل خطي على متغيرات توقع متعددة.

ما هو الانحدار الخطي؟

تُستخدم نماذج الانحدار الخطي لإظهار العلاقة بين أ متغير تابع ومستقل. عندما يكون هناك متغيران مستقلان أو أكثر يستخدمان في تحليل الانحدار ، فإن النموذج ليس مجرد نموذج خطي ولكنه نموذج انحدار متعدد.

يستخدم الانحدار الخطي البسيط للتنبؤ بقيمة متغير واحد باستخدام متغير آخر. يمثل الخط المستقيم العلاقة بين المتغيرين مع الانحدار الخطي.

هناك علاقة خطية بين متغير تابع بمتغيرين مستقلين أو أكثر في انحدار متعدد. يمكن أن تكون العلاقة أيضًا غير خطية ، ولن تتبع المتغيرات التابعة والمستقلة خطاً مستقيماً.

تمثيل تصويري لتنبؤات نموذج الانحدار الخطي المتعدد

يتم استخدام الانحدار الخطي وغير الخطي لتتبع الاستجابة باستخدام متغيرين أو أكثر. يتم إنشاء الانحدار غير الخطي من الافتراضات من التجربة والخطأ وهو صعب التنفيذ نسبيًا.

ما هو الانحدار الخطي المتعدد؟

الانحدار الخطي المتعدد هو أسلوب تحليل إحصائي يستخدم للتنبؤ بنتيجة متغير بناءً على متغيرين أو أكثر. إنه امتداد للانحدار الخطي ويعرف أيضًا باسم الانحدار المتعدد. المتغير الذي يجب توقعه هو المتغير التابع ، والمتغيرات المستخدمة للتنبؤ بقيمة المتغير التابع تُعرف بالمتغيرات المستقلة أو التفسيرية.

يتيح الانحدار الخطي المتعدد للمحللين تحديد تباين النموذج والمساهمة النسبية لكل متغير مستقل. الانحدار المتعدد نوعان ، الانحدار الخطي وغير الخطي.

صيغة الانحدار المتعدد

يتم التعبير عن الانحدار المتعدد مع ثلاثة متغيرات توقع (س) يتنبأ بالمتغير y بالمعادلة التالية:

ص = z0 + z1 * x1 + z2 * x2 + z3 * x3

تمثل قيم "z" أوزان الانحدار وهي معاملات بيتا . هم الارتباط بين متغير التوقع والنتيجة.

• yi هو متغير تابع أو متنبأ به
• z0 هو تقاطع y ، أي قيمة y عندما تكون x1 و x2 تساوي 0
• z1 و z2 هما معاملات الانحدار التي تمثل التغيير في y المرتبط بتغير وحدة واحدة في x1 و x2 على التوالي.

افتراضات الانحدار الخطي المتعدد

لقد عرفنا الملخص حول الانحدار المتعدد والصيغة الأساسية. ومع ذلك ، هناك بعض الافتراضات التي يعتمد عليها الانحدار الخطي المتعدد بالتفصيل على النحو التالي:

أنا. العلاقة بين المتغيرات التابعة والمستقلة

المتغير التابع يرتبط خطيًا بكل متغير مستقل. للتحقق من العلاقات الخطية ، يتم إنشاء مخطط مبعثر ويتم ملاحظته من أجل الخطية. إذا كانت علاقة مخطط التشتت غير خطية ، فسيتم تنفيذ انحدار غير خطي ، أو يتم نقل البيانات باستخدام برنامج إحصائي.

ثانيا. المتغيرات المستقلة ليست مرتبطة كثيرًا

يجب ألا تعرض البيانات علاقة خطية متعددة ، وهو ما يحدث في حالة ارتباط المتغيرات المستقلة ببعضها البعض بشكل كبير. سيخلق هذا مشاكل في جلب المتغير المحدد الذي يساهم في التباين في المتغير التابع.

ثالثا. التباين المتبقي ثابت

يفترض الانحدار الخطي المتعدد أن خطأ المتغيرات المتبقية متشابه في كل نقطة من النموذج الخطي. يُعرف هذا بالمثلية الجنسية. عند الانتهاء من تحليل البيانات ، يتم رسم القيم المتبقية القياسية مقابل القيم المتوقعة لتحديد ما إذا كانت النقاط موزعة بشكل صحيح عبر قيم المتغيرات المستقلة.

رابعا. استقلالية المراقبة

يجب أن تكون الملاحظات من بعضها البعض ، ويجب أن تكون القيم المتبقية مستقلة. تعمل إحصائية Durbin Watson بشكل أفضل لهذا الغرض.

تُظهر الطريقة القيم من 0 إلى 4 ، حيث تُظهر القيمة الواقعة بين 0 و 2 ارتباطًا إيجابيًا إيجابيًا ، ويظهر من 2 إلى 4 ارتباطًا تلقائيًا سلبيًا. نقطة المنتصف ، القيمة 2 ، توضح عدم وجود ارتباط تلقائي.

v. الوضع الطبيعي متعدد المتغيرات

تحدث الحالة الطبيعية متعددة المتغيرات مع المخلفات الموزعة بشكل طبيعي. لهذا الافتراض ، لوحظ كيف يتم توزيع قيم المخلفات. يمكن اختباره بطريقتين ،

· رسم بياني يوضح منحنى طبيعي متراكب و

· طريقة مؤامرة الاحتمالية العادية.

الحالات التي يتم فيها تطبيق الانحدار الخطي المتعدد

يعد الانحدار الخطي المتعدد جانبًا مهمًا جدًا من وجهة نظر المحلل. فيما يلي بعض الأمثلة حيث يمكن تطبيق المفهوم:

أنا. نظرًا لارتباط قيمة المتغير التابع بالمتغيرات المستقلة ، يتم استخدام الانحدار المتعدد للتنبؤ بالعائد المتوقع لمحصول عند هطول الأمطار ودرجة الحرارة ومستوى الأسمدة.

ثانيا. يستخدم تحليل الانحدار الخطي المتعدد أيضًا للتنبؤ بالاتجاهات والقيم المستقبلية. هذا مفيد بشكل خاص للتنبؤ بسعر الذهب في الأشهر الستة من الآن.

ثالثا. في مثال معين حيث يتم حذف العلاقة بين المسافة التي قطعها سائق UBER وعمر السائق وعدد سنوات خبرة السائق. في هذا الانحدار ، المتغير التابع هو المسافة التي قطعها سائق أوبر. المتغيرات المستقلة هي عمر السائق وعدد سنوات الخبرة في القيادة.

رابعا. مثال آخر حيث يتم استخدام تحليل الانحدار المتعدد في إيجاد العلاقة بين المعدل التراكمي لفصل من الطلاب وعدد الساعات التي يدرسونها وارتفاع الطلاب. المتغير التابع في هذا الانحدار هو المعدل التراكمي ، والمتغيرات المستقلة هي عدد ساعات الدراسة وأطوال الطلاب.

يمكن تحديد العلاقة بين راتب مجموعة من الموظفين في منظمة وعدد سنوات التنظيم عمر الموظفين من خلال تحليل الانحدار. المتغير التابع لهذا الانحدار هو الراتب ، والمتغيرات المستقلة هي خبرة الموظفين وعمرهم.

اقرأ أيضًا: 6 أنواع من نماذج الانحدار في التعلم الآلي التي يجب أن تعرفها

الانحدار الخطي المتعدد في R.

هناك العديد من الطرق التي يمكن بها تنفيذ الانحدار الخطي المتعدد ولكن يتم إجراؤه عادةً عبر البرامج الإحصائية. أحد أكثر البرامج استخدامًا هو R وهو مجاني وقوي ومتوفر بسهولة. سوف نتعلم أولاً خطوات إجراء الانحدار باستخدام R ، متبوعًا بمثال للفهم الواضح.

خطوات إجراء الانحدار المتعدد في R.

1. جمع البيانات: يتم جمع البيانات التي سيتم استخدامها في التنبؤ.
2. التقاط البيانات في R: التقاط البيانات باستخدام الكود واستيراد ملف CSV
3. التحقق من خطية البيانات باستخدام R: من المهم التأكد من وجود علاقة خطية بين المتغير التابع والمستقل. يمكن أن يتم ذلك باستخدام مخططات التشتت أو الكود في R.
4. تطبيق الانحدار الخطي المتعدد في R: استخدام الكود لتطبيق الانحدار الخطي المتعدد في R للحصول على مجموعة من المعاملات.
5. عمل التنبؤ باستخدام R: يتم تحديد القيمة المتوقعة في النهاية.

تنفيذ الانحدار المتعدد في R

سوف نفهم كيف يتم تنفيذ R عندما يتم إجراء مسح في عدد معين من الأماكن بواسطة باحثي الصحة العامة لجمع البيانات عن السكان الذين يدخنون ، والذين يسافرون إلى العمل ، والأشخاص الذين يعانون من أمراض القلب.

دليل خطوة بخطوة للانحدار الخطي المتعدد في R:

أنا. قم بتحميل مجموعة بيانات heart.data وقم بتشغيل التعليمات البرمجية التالية

lm <-lm (مرض القلب ~ ركوب الدراجات + التدخين ، البيانات = بيانات القلب)

مجموعة البيانات القلب. تحسب البيانات تأثير المتغيرات المستقلة ركوب الدراجات والتدخين على مرض القلب المتغير التابع باستخدام "lm ()" (معادلة النموذج الخطي).

ثانيا. تفسير النتائج

استخدم وظيفة الملخص () لعرض نتائج النموذج:

الملخص (heart.disease.lm)

تضع هذه الوظيفة أهم المعلمات التي تم الحصول عليها من النموذج الخطي في جدول يبدو على النحو التالي:

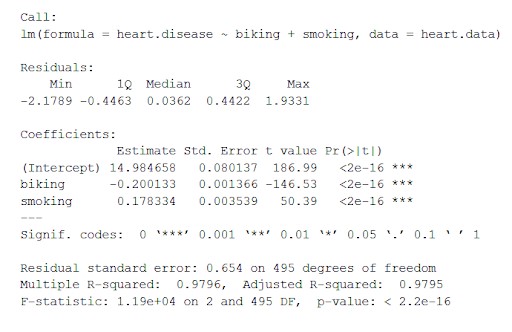
من هذا الجدول يمكننا أن نستنتج:

• صيغة "Call" ،
• بقايا النموذج ("المخلفات"). إذا كانت المخلفات تتركز تقريبًا حول الصفر وبانتشار مماثل على كلا الجانبين (الوسيط 0.03 ، والحد الأدنى والحد الأقصى -2 و 2) ، فإن النموذج يناسب افتراضات عدم التجانس.
• معاملات الانحدار للنموذج ("المعاملات").

الصف 1 من جدول المعاملات (التقاطع): هذا هو تقاطع y لمعادلة الانحدار ويستخدم لمعرفة التقاطع المقدر لتعويض معادلة الانحدار والتنبؤ بقيم المتغير التابع.

أمراض القلب = 15 + (-0.2 * ركوب الدراجة) + (0.178 * تدخين) ± هـ

بعض المصطلحات المتعلقة بالانحدار المتعدد

أنا. عمود التقدير : هو التأثير المقدر ويسمى أيضًا معامل الانحدار أو قيمة r2. تشير التقديرات إلى أنه مقابل كل زيادة بنسبة 1 في المائة في ركوب الدراجات في العمل ، هناك انخفاض مصاحب بنسبة 0.2 في المائة في أمراض القلب ، ولكل زيادة في المائة في التدخين هناك زيادة بنسبة 17 في المائة في أمراض القلب.

ثانيا. Std.error : يعرض الخطأ القياسي من التقدير. هذا رقم يظهر تباينًا حول تقديرات معامل الانحدار.

ثالثا. قيمة t : تعرض إحصائية الاختبار . إنها قيمة t من اختبار t على الوجهين .

رابعا. Pr (> | t |) : إنها p -value التي تظهر احتمالية حدوث t -value.

الإبلاغ عن النتائج

يجب أن ندرج التأثير المقدر وخطأ التقدير المعياري والقيمة p .

في المثال أعلاه ، تم العثور على العلاقات المهمة بين تكرار ركوب الدراجات في العمل وأمراض القلب وتكرار التدخين وأمراض القلب لتكون p <0.001.

ينخفض ​​معدل الإصابة بأمراض القلب بنسبة 0.2٪ (أو ± 0.0014) لكل 1٪ زيادة في ركوب الدراجات. يزداد معدل الإصابة بأمراض القلب بنسبة 0.178٪ (أو ± 0.0035) لكل 1٪ زيادة في التدخين.

تمثيل رسومي للنتائج

يمكن إظهار تأثيرات المتغيرات المستقلة المتعددة على المتغير التابع في رسم بياني. في هذا ، يمكن رسم متغير مستقل واحد فقط على المحور x.

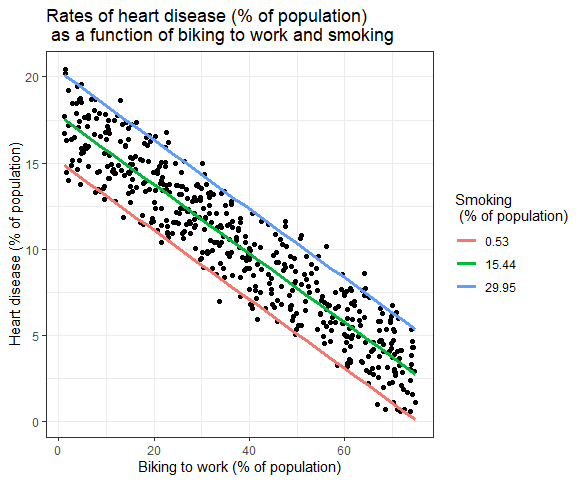
الانحدار الخطي المتعدد: تمثيل رسومي

هنا ، يتم رسم القيم المتوقعة للمتغير التابع (مرض القلب) عبر القيم المرصودة للنسبة المئوية للأشخاص الذين يركبون الدراجات إلى العمل.

لتأثير التدخين على المتغير المستقل ، يتم حساب القيم المتوقعة ، مع إبقاء التدخين ثابتًا عند الحد الأدنى والمتوسط ​​والحد الأقصى لمعدلات التدخين.

اقرأ أيضًا: الانحدار الخطي مقابل الانحدار الخطي. الانحدار اللوجستي: الفرق بين الانحدار الخطي والانحدار اللوجستي

الكلمات الأخيرة

هذا يمثل نهاية منشور المدونة هذا. لقد بذلنا قصارى جهدنا لنوضح لك مفهوم الانحدار الخطي المتعدد وكيف يتم تنفيذ الانحدار المتعدد في R لتسهيل تحليل التنبؤ.

إذا كنت حريصًا على تأييد رحلتك في علم البيانات وتعلم المزيد من مفاهيم R والعديد من اللغات الأخرى لتعزيز حياتك المهنية ، فانضم إلى upGrad . نحن نقدم برنامج الشهادة المتقدم في علوم البيانات المصمم خصيصًا للمهنيين العاملين ويتضمن أكثر من 300 ساعة من التعلم مع الإرشاد المستمر.