R中的多元线性回归[带图表和示例]

作为一名数据科学家，您经常被要求在许多项目中进行预测分析。 分析是一种统计方法，用于建立因变量与一组自变量之间的关系。 整个概念可以称为线性回归，它基本上有两种类型：简单线性回归和多元线性回归。

R 是数据科学和分析方面最重要的语言之一， R 中的多元线性回归也是如此。 它描述了单个响应变量 Y 线性依赖于多个预测变量的场景。

什么是线性回归？

线性回归模型用于显示或预测一个 因变量和自变量。 当回归分析中使用两个或多个自变量时，该模型不是简单的线性而是多元回归模型。

简单线性回归用于通过使用另一个变量来预测一个变量的值。 一条直线用线性回归表示两个变量之间的关系。

在多元回归中，因变量与两个或多个自变量之间存在线性关系。 这种关系也可以是非线性的，因变量和自变量不会遵循一条直线。

多元线性回归模型预测的图示

线性和非线性回归用于跟踪使用两个或多个变量的响应。 非线性回归是根据反复试验的假设创建的，并且相对难以执行。

什么是多元线性回归？

多元线性回归是一种统计分析技术，用于根据两个或多个变量预测变量的结果。 它是线性回归的扩展，也称为多元回归。 要预测的变量是因变量，用于预测因变量值的变量称为自变量或解释变量。

多元线性回归使分析师能够确定模型的变化和每个自变量的相对贡献。 多元回归有两种类型，线性回归和非线性回归。

多元回归公式

具有三个预测变量 (x) 预测变量 y 的多元回归表示为以下等式：

y = z0 + z1*x1 + z2*x2 + z3*x3

“z”值代表回归权重，是beta 系数。 它们是预测变量和结果之间的关联。

• yi是因变量或预测变量
• z0是y截距，即x1和x2为0时y的值
• z1和z2是回归系数，分别表示与x1和x2的一个单位变化相关的 y 变化。

多元线性回归的假设

我们已经知道了关于多元回归和基本公式的简介。 但是，有一些假设是多元线性回归所基于的，具体如下：

一世。 因变量和自变量之间的关系

因变量与每个自变量线性相关。 为了检查线性关系，创建了一个散点图并观察其线性。 如果散点图关系是非线性的，则执行非线性回归，或使用统计软件传输数据。

ii. 自变量相关性不大

数据不应显示多重共线性，这种情况发生在自变量相互高度相关的情况下。 这将在提取导致因变量方差的特定变量时产生问题。

iii. 残差是常数

多元线性回归假设其余变量的误差在线性模型的每个点上都相似。 这被称为同方差性。 当数据分析完成时，标准残差与预测值的关系被绘制出来，以确定这些点是否正确分布在自变量的值上。

iv. 观察独立

观测值应该是相互的，残差值应该是独立的。 Durbin Watson 统计数据最适合这一点。

该方法显示从 0 到 4 的值，其中 0 到 2 之间的值表示正自相关，从 2 到 4 表示负自相关。 中点值为 2，表示不存在自相关。

v.多元正态性

多元正态性发生在正态分布的残差上。 对于这个假设，观察残差值是如何分布的。 它可以使用两种方法进行测试，

· 显示叠加正态曲线的直方图和

· 正态概率图法。

应用多元线性回归的实例

从分析师的角度来看，多元线性回归是一个非常重要的方面。 以下是该概念适用的一些示例：

一世。 由于因变量的值与自变量相关，因此使用多元回归来预测作物在特定降雨、温度和肥料水平下的预期产量。

ii. 多元线性回归分析也用于预测趋势和未来值。 这对于预测从现在起六个月内的黄金价格特别有用。

iii. 在一个特定的例子中，UBER 司机所行驶的距离与司机的年龄和司机的经验年数之间的关系被去掉了。 在这个回归中，因变量是 UBER 司机覆盖的距离。 自变量是驾驶员的年龄和驾驶经验的年数。

iv. 另一个例子是使用多元回归分析来寻找一个班级学生的 GPA 与他们学习的小时数和学生身高之间的关系。 该回归中的因变量是 GPA，自变量是学习时间和学生的身高。

v. 一个组织中一组员工的工资与组织工作年限之间的关系可以通过回归分析确定员工年龄。 该回归的因变量是工资，自变量是员工的经验和年龄。

另请阅读：您应该了解的机器学习中的 6 种回归模型

R中的多元线性回归

可以通过多种方式执行多元线性回归，但通常通过统计软件完成。 最常用的软件之一是 R，它免费、强大且易于使用。 我们将首先学习使用 R 执行回归的步骤，然后是一个清晰理解的示例。

在 R 中执行多重回归的步骤

1. 数据采集​​： 收集要在预测中使用的数据。
2. R 中的数据捕获：使用代码捕获数据并导入 CSV 文件
3. 用 R 检查数据线性： 确保因变量和自变量之间存在线性关系非常重要。 可以使用散点图或 R 中的代码来完成
4. 在 R 中应用多元线性回归： 使用代码在 R 中应用多元线性回归以获得一组系数。
5. 使用 R 进行预测： 最后确定预测值。

R中的多重回归实现

当公共卫生研究人员在一定数量的地方进行一项调查以收集有关吸烟人口、上班人员和心脏病患者的数据时，我们将了解 R 是如何实施的。

R中多元线性回归的分步指南：

一世。 加载 heart.data 数据集并运行以下代码

lm<-lm(heart.disease ~ 骑车 + 吸烟, data = heart.data)

数据集心脏。 数据使用“lm()”（线性模型的方程）计算自变量骑自行车和吸烟对因变量心脏病的影响。

ii. 解释结果

使用 summary() 函数查看模型的结果：

摘要（heart.disease.lm）

该函数将从线性模型中获得的最重要的参数放入一个表格中，如下所示：

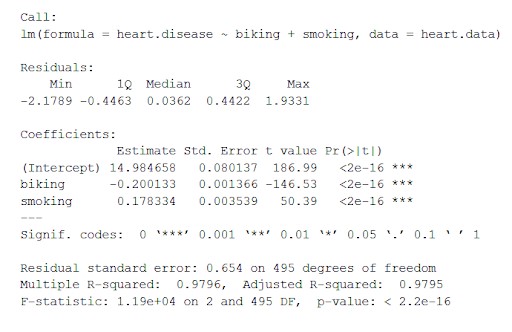
从这个表中我们可以推断：

• “呼叫”的公式，
• 模型的残差（“残差”）。 如果残差大致以零为中心并且在任一侧具有相似的散布（中位数 0.03，最小和最大 -2 和 2），则该模型符合异方差假设。
• 模型的回归系数（“系数”）。

系数表的第 1 行（截距）：这是回归方程的 y 截距，用于了解估计的截距以插入回归方程并预测因变量值。

心脏病 = 15 + (-0.2*骑自行车) + (0.178*吸烟) ± e

与多重回归相关的一些术语

一世。 Estimate Column ：估计效果，也称为回归系数或r2值。 估计表明，骑自行车上班每增加 1%，心脏病发病率就会降低 0.2%，而吸烟人数每增加 1%，心脏病发病率就会增加 0.17%。

ii. Std.error ：显示标准错误 的估计。 这个数字显示了回归系数估计值的变化。

iii. t 值：显示检验统计量。 它是来自双边t-test的t值。

iv. Pr( > | t | ) : 它是p值，表示t值出现的概率。

报告结果

我们应该包括估计效果、标准估计误差和p值。

在上面的例子中，发现骑自行车上班的频率与心脏病之间的显着关系以及吸烟和心脏病的频率之间的显着关系为 p < 0.001。

骑自行车每增加 1%，心脏病发病率就会降低 0.2%（或 ± 0.0014）。 吸烟每增加 1%，心脏病发病率增加 0.178%（或 ±0.0035）。

结果的图形表示

多个自变量对因变量的影响可以在图表中显示。 在这种情况下，只能在 x 轴上绘制一个自变量。

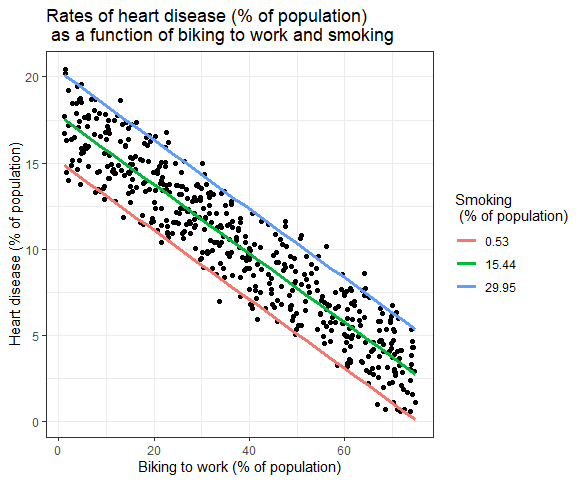
多元线性回归：图形表示

在这里，绘制了因变量（​​心脏病）的预测值与骑自行车上班的人数百分比的观察值之间的关系。

对于吸烟对自变量的影响，计算预测值，在最小、平均和最大吸烟率下保持吸烟不变。

另请阅读：线性回归与。 逻辑回归：线性回归和逻辑回归之间的区别

最后的话

这标志着这篇博文的结束。 我们已尽最大努力向您解释多元线性回归的概念以及如何实现 R 中的多元回归以简化预测分析。

如果您热衷于支持您的数据科学之旅并学习 R 和许多其他语言的更多概念以加强您的职业生涯，请加入upGrad 。 我们提供数据科学高级认证计划，该计划专为在职专业人士设计，包括 300 多个小时的学习和持续的指导。