Regresión lineal múltiple en R [con gráficos y ejemplos]

Como científico de datos, con frecuencia se le pide que realice análisis predictivos en muchos proyectos. Un análisis es un enfoque estadístico para establecer una relación entre una variable dependiente con un conjunto de variables independientes. Todo este concepto se puede denominar regresión lineal, que es básicamente de dos tipos: regresión lineal simple y múltiple.

R es uno de los lenguajes más importantes en términos de análisis y ciencia de datos, al igual que la regresión lineal múltiple en R tiene valor. Describe el escenario en el que una sola variable de respuesta Y depende linealmente de múltiples variables predictoras.

¿Qué es una regresión lineal?

Los modelos de regresión lineal se utilizan para mostrar o predecir la relación entre un dependiente y una variable independiente. Cuando se utilizan dos o más variables independientes en el análisis de regresión, el modelo no es simplemente lineal sino un modelo de regresión múltiple.

La regresión lineal simple se usa para predecir el valor de una variable usando otra variable. Una línea recta representa la relación entre las dos variables con regresión lineal.

Existe una relación lineal entre una variable dependiente con dos o más variables independientes en la regresión múltiple. La relación también puede ser no lineal y las variables dependientes e independientes no seguirán una línea recta.

Representación pictórica de las predicciones del modelo de regresión lineal múltiple

La regresión lineal y no lineal se usa para rastrear una respuesta usando dos o más variables. La regresión no lineal se crea a partir de suposiciones de prueba y error y es comparativamente difícil de ejecutar.

¿Qué es la regresión lineal múltiple?

La regresión lineal múltiple es una técnica de análisis estadístico utilizada para predecir el resultado de una variable en función de dos o más variables. Es una extensión de la regresión lineal y también conocida como regresión múltiple. La variable a predecir es la variable dependiente, y las variables utilizadas para predecir el valor de la variable dependiente se conocen como variables independientes o explicativas.

La regresión lineal múltiple permite a los analistas determinar la variación del modelo y la contribución relativa de cada variable independiente. La regresión múltiple es de dos tipos, regresión lineal y no lineal.

Fórmula de regresión múltiple

La regresión múltiple con tres variables predictoras (x) variable predictora y se expresa como la siguiente ecuación:

y = z0 + z1*x1 + z2*x2 + z3*x3

Los valores “z” representan los pesos de regresión y son los coeficientes beta . Son la asociación entre la variable predictora y el resultado.

• yi es variable dependiente o predicha
• z0 es la intersección con y, es decir, el valor de y cuando x1 y x2 son 0
• z1 y z2 son los coeficientes de regresión que representan el cambio en y relacionado con un cambio de una unidad en x1 y x2 , respectivamente.

Supuestos de regresión lineal múltiple

Hemos conocido el resumen sobre la regresión múltiple y la fórmula básica. Sin embargo, hay algunos supuestos en los que se basa la regresión lineal múltiple detallada a continuación:

I. Relación entre variables dependientes e independientes

La variable dependiente se relaciona linealmente con cada variable independiente. Para verificar las relaciones lineales, se crea un diagrama de dispersión y se observa la linealidad. Si la relación del gráfico de dispersión no es lineal, se realiza una regresión no lineal o los datos se transfieren mediante software estadístico.

ii. Las variables independientes no están muy correlacionadas

Los datos no deben mostrar multicolinealidad, lo que sucede en caso de que las variables independientes estén altamente correlacionadas entre sí. Esto creará problemas para obtener la variable específica que contribuye a la variación en la variable dependiente.

iii. La varianza residual es constante

La regresión lineal múltiple asume que el error de las variables restantes es similar en cada punto del modelo lineal. Esto se conoce como homocedasticidad. Cuando se realiza el análisis de datos, los residuos estándar frente a los valores pronosticados se trazan para determinar si los puntos se distribuyen correctamente entre los valores de las variables independientes.

IV. Independencia de la observación

Las observaciones deben ser unas de otras y los valores residuales deben ser independientes. La estadística de Durbin Watson funciona mejor para esto.

El método muestra valores de 0 a 4, donde un valor entre 0 y 2 muestra autocorrelación positiva, y de 2 a 4 muestra autocorrelación negativa. El punto medio, un valor de 2, muestra que no hay autocorrelación.

v. Normalidad multivariada

La normalidad multivariante ocurre con residuos normalmente distribuidos. Para este supuesto, se observa cómo se distribuyen los valores de los residuos. Se puede probar usando dos métodos,

· Un histograma que muestra una curva normal superpuesta y

· El método del gráfico de probabilidad normal.

Instancias donde se aplica la regresión lineal múltiple

La regresión lineal múltiple es un aspecto muy importante desde el punto de vista del analista. Estos son algunos de los ejemplos en los que el concepto puede ser aplicable:

I. Como el valor de la variable dependiente está correlacionado con las variables independientes, se utiliza la regresión múltiple para predecir el rendimiento esperado de un cultivo con cierta precipitación, temperatura y nivel de fertilizante.

ii. El análisis de regresión lineal múltiple también se utiliza para predecir tendencias y valores futuros. Esto es particularmente útil para predecir el precio del oro en los próximos seis meses.

iii. En un ejemplo particular donde se saca la relación entre la distancia recorrida por un conductor de UBER y la edad del conductor y el número de años de experiencia del conductor. En esta regresión, la variable dependiente es la distancia recorrida por el conductor de UBER. Las variables independientes son la edad del conductor y el número de años de experiencia en la conducción.

IV. Otro ejemplo donde se usa el análisis de regresión múltiple para encontrar la relación entre el GPA de una clase de estudiantes y la cantidad de horas que estudian y la altura de los estudiantes. La variable dependiente en esta regresión es el GPA, y las variables independientes son el número de horas de estudio y la estatura de los estudiantes.

v. La relación entre el salario de un grupo de empleados en una organización y el número de años de antigüedad de la organización, la edad de los empleados se puede determinar con un análisis de regresión. La variable dependiente para esta regresión es el salario y las variables independientes son la experiencia y la edad de los empleados.

Lea también: 6 tipos de modelos de regresión en el aprendizaje automático que debe conocer

Regresión lineal múltiple en R

Hay muchas formas en que se puede ejecutar la regresión lineal múltiple, pero comúnmente se realiza a través de software estadístico. Uno de los programas más utilizados es R, que es gratuito, potente y está disponible fácilmente. Primero aprenderemos los pasos para realizar la regresión con R, seguido de un ejemplo de comprensión clara.

Pasos para realizar una regresión múltiple en R

1. Recopilación de datos: Se recopilan los datos que se utilizarán en la predicción.
2. Captura de datos en R: capturar los datos usando el código e importar un archivo CSV
3. Comprobación de la linealidad de los datos con R: Es importante asegurarse de que exista una relación lineal entre la variable dependiente y la independiente. Se puede hacer usando diagramas de dispersión o el código en R
4. Aplicando Regresión Lineal Múltiple en R: Uso de código para aplicar regresión lineal múltiple en R para obtener un conjunto de coeficientes.
5. Haciendo predicciones con R: Al final se determina un valor predicho.

Implementación de Regresión Múltiple en R

Entenderemos cómo se implementa R cuando los investigadores de salud pública realizan una encuesta en un cierto número de lugares para recopilar los datos sobre la población que fuma, que viaja al trabajo y las personas con una enfermedad cardíaca.

Guía paso a paso para la regresión lineal múltiple en R:

I. Cargue el conjunto de datos heart.data y ejecute el siguiente código

lm<-lm(corazón.enfermedad ~ andar en bicicleta + fumar, datos = corazón.datos)

El corazón del conjunto de datos. Data calcula el efecto de las variables independientes andar en bicicleta y fumar sobre la variable dependiente enfermedad cardiaca usando 'lm()' (la ecuación para el modelo lineal).

ii. Interpretación de resultados

utilice la función summary() para ver los resultados del modelo:

resumen(corazón.enfermedad.lm)

Esta función coloca los parámetros más importantes obtenidos del modelo lineal en una tabla que se ve a continuación:

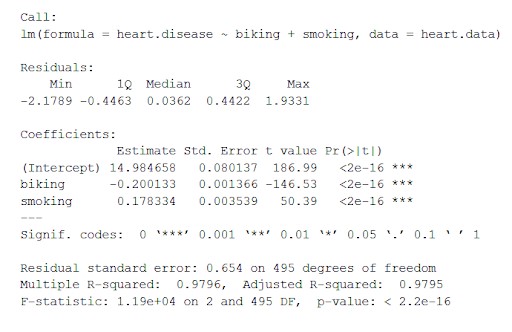
De esta tabla podemos inferir:

• La fórmula de 'Llamada',
• Los residuos del modelo ('Residuals'). Si los residuos están aproximadamente centrados alrededor de cero y con una dispersión similar en ambos lados (mediana 0,03 y mínimo y máximo -2 y 2), entonces el modelo se ajusta a los supuestos de heteroscedasticidad.
• Los coeficientes de regresión del modelo ('Coeficientes').

Fila 1 de la tabla de coeficientes (intersección): esta es la intersección y de la ecuación de regresión y se usa para conocer la intersección estimada para introducir la ecuación de regresión y predecir los valores de la variable dependiente.

cardiopatía = 15 + (-0,2*ciclismo) + (0,178*fumar) ± e

Algunos términos relacionados con la regresión múltiple

I. Columna Estimación : Es el efecto estimado y también se le llama coeficiente de regresión o valor r2. Las estimaciones indican que por cada aumento del uno por ciento en ir en bicicleta al trabajo hay una disminución asociada del 0,2 por ciento en las enfermedades cardíacas, y por cada aumento porcentual en el tabaquismo hay un aumento del 0,17 por ciento en las enfermedades cardíacas.

ii. Std.error : Muestra el error estándar de la estimación. Este es un número que muestra variación en torno a las estimaciones del coeficiente de regresión.

iii. Valor t : Muestra el estadístico de la prueba . Es un valor t de una prueba t de dos colas .

IV. Pr( > | t | ) : Es el valor p que muestra la probabilidad de ocurrencia del valor t .

Informe de los resultados

Deberíamos incluir el efecto estimado, el error de estimación estándar y el valor p .

En el ejemplo anterior, se encontró que las relaciones significativas entre la frecuencia de ir en bicicleta al trabajo y las enfermedades del corazón y la frecuencia de fumar y las enfermedades del corazón eran p < 0,001.

La frecuencia de enfermedades del corazón se reduce en un 0,2 % (o ± 0,0014) por cada 1 % de aumento en el ciclismo. La frecuencia de enfermedades cardíacas aumenta en un 0,178% (o ± 0,0035) por cada 1% de aumento en el tabaquismo.

Representación gráfica de los hallazgos

Los efectos de múltiples variables independientes sobre la variable dependiente se pueden mostrar en un gráfico. En esto, solo se puede trazar una variable independiente en el eje x.

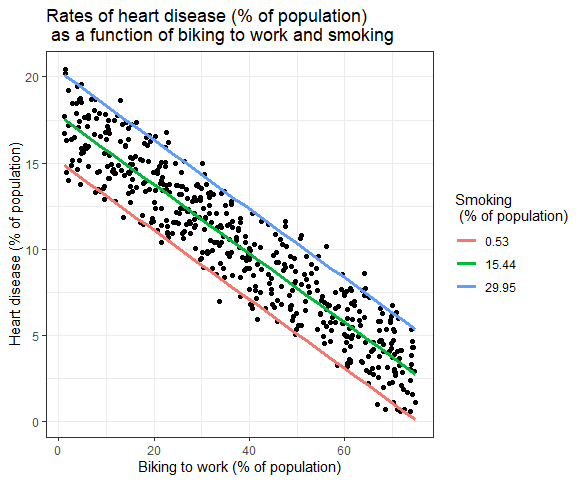
Regresión lineal múltiple: representación gráfica

Aquí, se trazan los valores pronosticados de la variable dependiente (enfermedad cardíaca) a través de los valores observados para el porcentaje de personas que van en bicicleta al trabajo.

Para el efecto del tabaquismo sobre la variable independiente, se calculan los valores predichos, manteniendo el tabaquismo constante en las tasas mínima, media y máxima de tabaquismo.

Lea también: Regresión lineal vs. Regresión logística: diferencia entre regresión lineal y regresión logística

Ultimas palabras

Esto marca el final de esta publicación de blog. Hemos hecho todo lo posible para explicarle el concepto de regresión lineal múltiple y cómo se implementa la regresión múltiple en R para facilitar el análisis de predicción.

Si está interesado en respaldar su viaje de ciencia de datos y aprender más conceptos de R y muchos otros lenguajes para fortalecer su carrera, únase a upGrad . Ofrecemos el Programa de Certificación Avanzada en Ciencia de Datos, que está especialmente diseñado para profesionales que trabajan e incluye más de 300 horas de aprendizaje con tutoría continua.