Regresi Linier Berganda di R [Dengan Grafik & Contoh]

Sebagai ilmuwan data, Anda sering diminta untuk membuat analisis prediktif di banyak proyek. Analisis adalah pendekatan statistik untuk menetapkan hubungan antara variabel dependen dengan sekumpulan variabel independen. Seluruh konsep ini dapat disebut sebagai regresi linier, yang pada dasarnya terdiri dari dua jenis: regresi linier sederhana dan berganda.

R adalah salah satu bahasa yang paling penting dalam hal ilmu data dan analitik, dan begitu juga regresi linier berganda dalam R memegang nilai. Ini menggambarkan skenario di mana variabel respons tunggal Y bergantung secara linier pada beberapa variabel prediktor.

Apa itu Regresi Linier?

Model regresi linier digunakan untuk menunjukkan atau memprediksi hubungan antara tergantung dan variabel bebas. Ketika ada dua atau lebih variabel independen yang digunakan dalam analisis regresi, modelnya tidak hanya linier tetapi model regresi berganda.

Regresi linier sederhana digunakan untuk memprediksi nilai suatu variabel dengan menggunakan variabel lain. Garis lurus mewakili hubungan antara dua variabel dengan regresi linier.

Terdapat hubungan linier antara satu variabel terikat dengan dua atau lebih variabel bebas dalam regresi berganda. Hubungannya juga bisa non-linier, dan variabel dependen dan independen tidak akan mengikuti garis lurus.

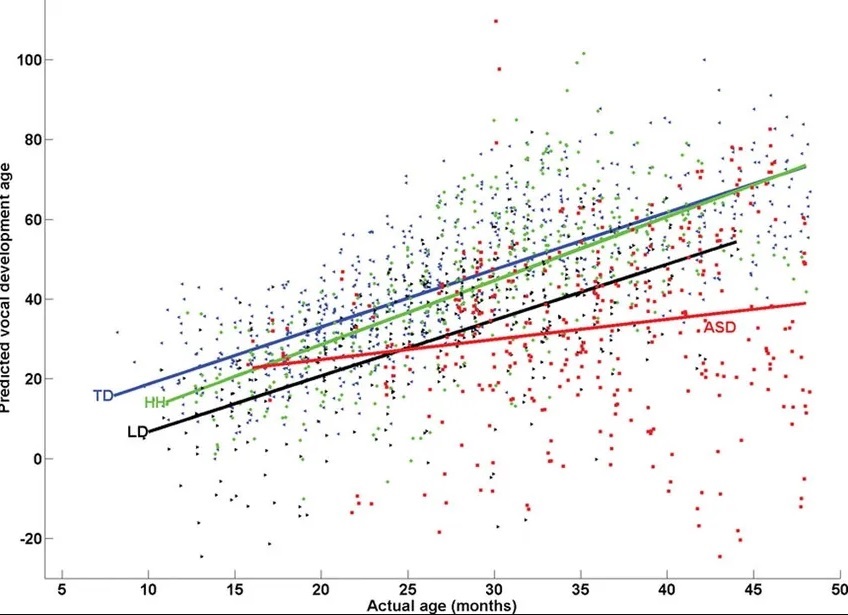
Representasi bergambar dari prediksi model regresi linier berganda

Regresi linier dan non-linier digunakan untuk melacak respons menggunakan dua atau lebih variabel. Regresi non-linier dibuat dari asumsi dari trial and error dan relatif sulit untuk dieksekusi.

Apa itu Regresi Linier Berganda?

Regresi linier berganda adalah teknik analisis statistik yang digunakan untuk memprediksi hasil suatu variabel berdasarkan dua variabel atau lebih. Ini adalah perpanjangan dari regresi linier dan juga dikenal sebagai regresi berganda. Variabel yang akan diprediksi adalah variabel dependen, dan variabel yang digunakan untuk memprediksi nilai variabel dependen dikenal sebagai variabel independen atau penjelas.

Regresi linier berganda memungkinkan analis untuk menentukan variasi model dan kontribusi relatif masing-masing variabel independen. Regresi berganda terdiri dari dua jenis, regresi linier dan non-linier.

Rumus Regresi Berganda

Regresi berganda dengan tiga variabel prediktor (x) variabel prediksi y dinyatakan sebagai persamaan berikut:

y = z0 + z1*x1 + z2*x2 + z3*x3

Nilai “z” mewakili bobot regresi dan merupakan koefisien beta . Mereka adalah hubungan antara variabel prediktor dan hasilnya.

• yi adalah variabel dependen atau diprediksi
• z0 adalah perpotongan y, yaitu nilai y ketika x1 dan x2 adalah 0
• z1 dan z2 adalah koefisien regresi yang mewakili perubahan y terkait dengan perubahan satu unit di x1 dan x2 , masing-masing.

Asumsi Regresi Linier Berganda

Kita telah mengetahui secara singkat tentang regresi berganda dan rumus dasarnya. Namun, ada beberapa asumsi yang mendasari regresi linier berganda seperti di bawah ini:

saya. Hubungan Antara Variabel Dependen dan Variabel Independen

Variabel terikat berhubungan secara linier dengan masing-masing variabel bebas. Untuk memeriksa hubungan linier, dibuat scatterplot dan diamati linieritasnya. Jika hubungan scatterplot bersifat non-linier, maka dilakukan regresi non-linier, atau data dipindahkan menggunakan perangkat lunak statistik.

ii. Variabel Independen Tidak Banyak Berkorelasi

Data tidak boleh menampilkan multikolinearitas, yang terjadi jika variabel independen sangat berkorelasi satu sama lain. Ini akan menimbulkan masalah dalam mengambil variabel spesifik yang berkontribusi terhadap varians dalam variabel dependen.

aku aku aku. Varians Residual adalah Konstan

Regresi linier berganda mengasumsikan bahwa kesalahan variabel yang tersisa serupa pada setiap titik model linier. Ini dikenal sebagai homoskedastisitas. Ketika analisis data selesai, residual standar terhadap nilai prediksi diplot untuk menentukan apakah titik-titik tersebut didistribusikan dengan benar di seluruh nilai variabel independen.

iv. Kemandirian Pengamatan

Pengamatan harus satu sama lain, dan nilai sisa harus independen. Statistik Durbin Watson bekerja paling baik untuk ini.

Metode tersebut menunjukkan nilai dari 0 hingga 4, dimana nilai antara 0 dan 2 menunjukkan autokorelasi positif, dan dari 2 hingga 4 menunjukkan autokorelasi negatif. Titik tengah, nilai 2, menunjukkan tidak ada autokorelasi.

v. Normalitas Multivariat

Normalitas multivariat terjadi dengan residual yang terdistribusi normal. Untuk asumsi ini, diamati bagaimana nilai-nilai residual didistribusikan. Hal ini dapat diuji dengan menggunakan dua metode,

· Histogram yang menunjukkan kurva normal yang ditumpangkan dan

· Metode Plot Probabilitas Normal.

Contoh Di mana Regresi Linier Berganda Diterapkan

Regresi linier berganda merupakan aspek yang sangat penting dari sudut pandang seorang analis. Berikut adalah beberapa contoh di mana konsep tersebut dapat diterapkan:

saya. Karena nilai variabel dependen berkorelasi dengan variabel independen, regresi berganda digunakan untuk memprediksi hasil yang diharapkan dari suatu tanaman pada curah hujan, suhu, dan tingkat pemupukan tertentu.

ii. Analisis regresi linier berganda juga digunakan untuk memprediksi tren dan nilai masa depan. Ini sangat berguna untuk memprediksi harga emas dalam enam bulan dari sekarang.

aku aku aku. Dalam contoh tertentu di mana hubungan antara jarak yang ditempuh oleh pengemudi UBER dan usia pengemudi dan jumlah tahun pengalaman pengemudi dihilangkan. Dalam regresi ini, variabel terikatnya adalah jarak yang ditempuh oleh pengemudi UBER. Variabel bebasnya adalah umur pengemudi dan jumlah tahun pengalaman mengemudi.

iv. Contoh lain di mana analisis regresi berganda digunakan dalam mencari hubungan antara IPK kelas siswa dan jumlah jam mereka belajar dan tinggi badan siswa. Variabel terikat dalam regresi ini adalah IPK, sedangkan variabel bebasnya adalah jumlah jam belajar dan tinggi badan siswa.

v. Hubungan antara gaji sekelompok karyawan dalam suatu organisasi dan jumlah tahun bekerja dengan usia karyawan dapat ditentukan dengan analisis regresi. Variabel terikat untuk regresi ini adalah gaji, dan variabel bebasnya adalah pengalaman dan usia karyawan.

Baca Juga: 6 Jenis Model Regresi dalam Machine Learning Yang Harus Anda Ketahui

Regresi Linier Berganda di R

Ada banyak cara regresi linier berganda dapat dijalankan tetapi biasanya dilakukan melalui perangkat lunak statistik. Salah satu perangkat lunak yang paling banyak digunakan adalah R yang gratis, kuat, dan tersedia dengan mudah. Pertama-tama kita akan mempelajari langkah-langkah untuk melakukan regresi dengan R, diikuti dengan contoh pemahaman yang jelas.

Langkah-Langkah Melakukan Regresi Berganda di R

1. Pengumpulan data: Data yang akan digunakan dalam prediksi dikumpulkan.
2. Pengambilan Data di R: Menangkap data menggunakan kode dan mengimpor file CSV
3. Memeriksa Linearitas Data dengan R: Penting untuk memastikan bahwa ada hubungan linier antara variabel dependen dan variabel independen. Itu dapat dilakukan dengan menggunakan plot pencar atau kode dalam R
4. Menerapkan Regresi Linier Berganda di R: Menggunakan kode untuk menerapkan regresi linier berganda di R untuk mendapatkan satu set koefisien.
5. Membuat Prediksi dengan R: Nilai prediksi ditentukan di akhir.

Implementasi Regresi Berganda di R

Kita akan memahami bagaimana R diimplementasikan ketika survei dilakukan di sejumlah tempat tertentu oleh peneliti kesehatan masyarakat untuk mengumpulkan data tentang populasi yang merokok, yang bepergian ke tempat kerja, dan orang-orang dengan penyakit jantung.

Panduan Langkah-demi-Langkah untuk Regresi Linier Berganda di R:

saya. Muat dataset heart.data dan jalankan kode berikut

lm<-lm(penyakit jantung ~ bersepeda + merokok, data = jantung.data)

Dataset hati. Data menghitung pengaruh variabel independen bersepeda dan merokok pada variabel dependen penyakit jantung menggunakan 'lm()' (persamaan untuk model linier).

ii. Menafsirkan Hasil

gunakan fungsi summary() untuk melihat hasil model:

ringkasan(jantung.penyakit.lm)

Fungsi ini menempatkan parameter terpenting yang diperoleh dari model linier ke dalam tabel yang terlihat seperti di bawah ini:

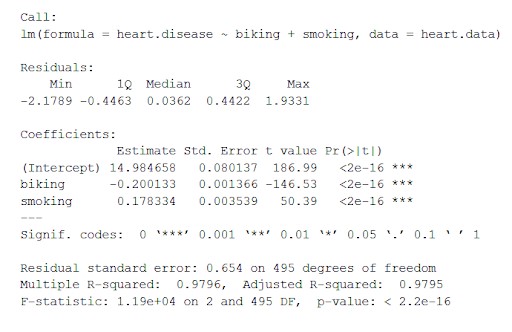
Dari tabel ini kita dapat menyimpulkan:

• Rumus 'Panggilan',
• Residu model ('Residual'). Jika residual secara kasar berpusat di sekitar nol dan dengan penyebaran yang sama di kedua sisi (median 0,03, dan min dan maks -2 dan 2), maka model tersebut sesuai dengan asumsi heteroskedastisitas.
• Koefisien regresi model ('Koefisien').

Baris 1 dari tabel koefisien (Intercept): Ini adalah intersep y dari persamaan regresi dan digunakan untuk mengetahui estimasi intersep untuk memasukkan persamaan regresi dan memprediksi nilai variabel dependen.

penyakit jantung = 15 + (-0,2*bersepeda) + (0,178*merokok) ± e

Beberapa Istilah Terkait Regresi Berganda

saya. Kolom Estimasi : Ini adalah efek estimasi dan disebut juga koefisien regresi atau nilai r2. Perkiraan mengatakan bahwa untuk setiap satu persen peningkatan bersepeda ke tempat kerja ada penurunan 0,2 persen terkait penyakit jantung, dan untuk setiap persen peningkatan merokok ada peningkatan 0,17 persen penyakit jantung.

ii. Std.error : Ini menampilkan kesalahan standar dari perkiraan. Ini adalah angka yang menunjukkan variasi di sekitar perkiraan koefisien regresi.

aku aku aku. Nilai t : Menampilkan statistik uji . Ini adalah nilai - t dari uji-t dua sisi .

iv. Pr( > | t | ) : Merupakan nilai p yang menunjukkan peluang terjadinya nilai t .

Melaporkan Hasil

Kita harus memasukkan efek yang diperkirakan, kesalahan estimasi standar, dan nilai- p .

Dalam contoh di atas, hubungan yang signifikan antara frekuensi bersepeda ke tempat kerja dan penyakit jantung dan frekuensi merokok dan penyakit jantung ditemukan p <0,001.

Frekuensi penyakit jantung menurun sebesar 0,2% (atau ± 0,0014) untuk setiap 1% peningkatan bersepeda. Frekuensi penyakit jantung meningkat sebesar 0,178% (atau ± 0,0035) untuk setiap 1% peningkatan merokok.

Representasi Grafis dari Temuan

Pengaruh beberapa variabel independen terhadap variabel dependen dapat ditunjukkan dalam grafik. Dalam hal ini, hanya satu variabel independen yang dapat diplot pada sumbu x.

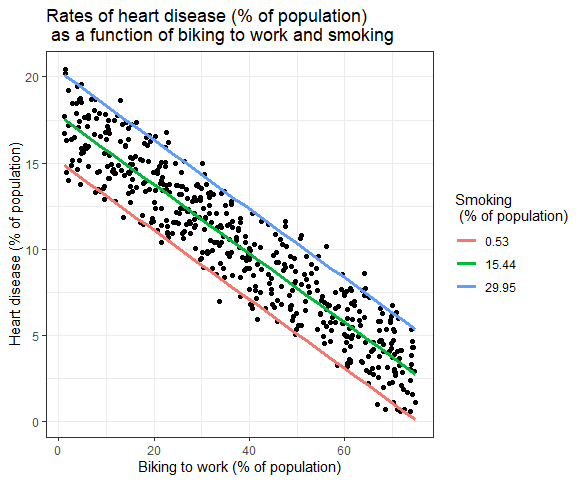
Regresi Linier Berganda: Representasi Grafis

Di sini, nilai prediksi variabel dependen (penyakit jantung) di seluruh nilai yang diamati untuk persentase orang yang bersepeda ke tempat kerja diplot.

Untuk pengaruh merokok pada variabel independen, nilai prediksi dihitung, menjaga merokok konstan pada tingkat minimum, rata-rata, dan maksimum merokok.

Baca Juga: Regresi Linier Vs. Regresi Logistik: Perbedaan Antara Regresi Linier & Regresi Logistik

Kata-kata Terakhir

Ini menandai akhir dari posting blog ini. Kami telah mencoba yang terbaik dari upaya kami untuk menjelaskan kepada Anda konsep regresi linier berganda dan bagaimana regresi berganda di R diimplementasikan untuk memudahkan analisis prediksi.

Jika Anda ingin mendukung perjalanan ilmu data Anda dan mempelajari lebih banyak konsep R dan banyak bahasa lain untuk memperkuat karier Anda, bergabunglah dengan upGrad . Kami menawarkan Program Sertifikasi Lanjutan dalam Ilmu Data yang dirancang khusus untuk para profesional yang bekerja dan mencakup 300+ jam pembelajaran dengan bimbingan berkelanjutan.