Regressione lineare multipla in R [con grafici ed esempi]

In qualità di data scientist, ti viene spesso chiesto di effettuare analisi predittive in molti progetti. Un'analisi è un approccio statistico per stabilire una relazione tra una variabile dipendente con un insieme di variabili indipendenti. L'intero concetto può essere definito come una regressione lineare, che è fondamentalmente di due tipi: regressione lineare semplice e multipla.

R è uno dei linguaggi più importanti in termini di scienza dei dati e analisi, così come la regressione lineare multipla in R ha valore. Descrive lo scenario in cui una singola variabile di risposta Y dipende linearmente da più variabili predittive.

Che cos'è una regressione lineare?

I modelli di regressione lineare vengono utilizzati per mostrare o prevedere la relazione tra a dipendente e una variabile indipendente. Quando nell'analisi di regressione vengono utilizzate due o più variabili indipendenti, il modello non è semplicemente lineare, ma è un modello di regressione multipla.

La regressione lineare semplice viene utilizzata per prevedere il valore di una variabile utilizzando un'altra variabile. Una retta rappresenta la relazione tra le due variabili con regressione lineare.

Esiste una relazione lineare tra una variabile dipendente con due o più variabili indipendenti in regressione multipla. La relazione può anche essere non lineare e le variabili dipendenti e indipendenti non seguiranno una linea retta.

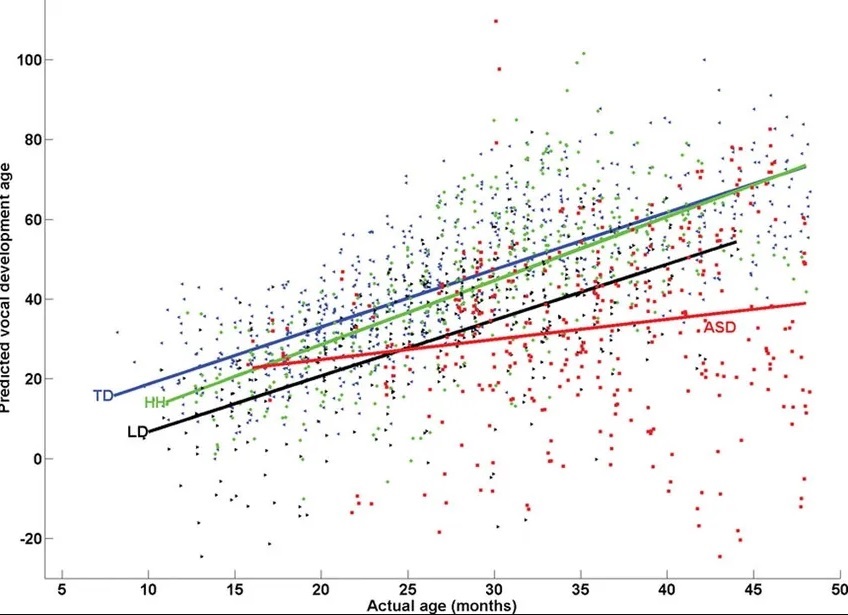
Rappresentazione pittorica di previsioni del modello di regressione lineare multipla

La regressione lineare e non lineare viene utilizzata per tenere traccia di una risposta utilizzando due o più variabili. La regressione non lineare è creata da ipotesi di tentativi ed errori ed è relativamente difficile da eseguire.

Che cos'è la regressione lineare multipla?

La regressione lineare multipla è una tecnica di analisi statistica utilizzata per prevedere il risultato di una variabile sulla base di due o più variabili. È un'estensione della regressione lineare e nota anche come regressione multipla. La variabile da prevedere è la variabile dipendente e le variabili utilizzate per prevedere il valore della variabile dipendente sono note come variabili indipendenti o esplicative.

La regressione lineare multipla consente agli analisti di determinare la variazione del modello e il contributo relativo di ciascuna variabile indipendente. La regressione multipla è di due tipi, lineare e non lineare.

Formula di regressione multipla

La regressione multipla con tre variabili predittive (x) variabile predittiva y è espressa come la seguente equazione:

y = z0 + z1*x1 + z2*x2 + z3*x3

I valori “z” rappresentano i pesi di regressione e sono i coefficienti beta . Sono l'associazione tra la variabile predittiva e il risultato.

• yi è una variabile dipendente o prevista
• z0 è l'intercetta y, cioè il valore di y quando x1 e x2 sono 0
• z1 e z2 sono i coefficienti di regressione che rappresentano la variazione di y relativa a una variazione di un'unità rispettivamente in x1 e x2 .

Assunzioni di regressione lineare multipla

Abbiamo conosciuto il brief sulla regressione multipla e la formula di base. Tuttavia, ci sono alcune ipotesi su cui si basa la regressione lineare multipla dettagliata come di seguito:

io. Relazione tra variabili dipendenti e indipendenti

La variabile dipendente si relaziona linearmente con ciascuna variabile indipendente. Per verificare le relazioni lineari, viene creato un grafico a dispersione e viene osservata la linearità. Se la relazione del grafico a dispersione non è lineare, viene eseguita una regressione non lineare oppure i dati vengono trasferiti utilizzando un software statistico.

ii. Le variabili indipendenti non sono molto correlate

I dati non dovrebbero mostrare multicollinearità, cosa che si verifica nel caso in cui le variabili indipendenti siano altamente correlate tra loro. Ciò creerà problemi nel recuperare la variabile specifica che contribuisce alla varianza nella variabile dipendente.

iii. La varianza residua è costante

La regressione lineare multipla presuppone che l'errore delle variabili rimanenti sia simile in ogni punto del modello lineare. Questo è noto come omoscedasticità. Al termine dell'analisi dei dati, i residui standard rispetto ai valori previsti vengono tracciati per determinare se i punti sono distribuiti correttamente tra i valori delle variabili indipendenti.

IV. Osservazione Indipendenza

Le osservazioni dovrebbero essere l'una dell'altra ei valori residui dovrebbero essere indipendenti. La statistica di Durbin Watson funziona meglio per questo.

Il metodo mostra valori da 0 a 4, dove un valore compreso tra 0 e 2 mostra un'autocorrelazione positiva e da 2 a 4 mostra un'autocorrelazione negativa. Il punto medio, un valore di 2, mostra che non c'è autocorrelazione.

v. Normalità multivariata

La normalità multivariata si verifica con i residui normalmente distribuiti. Per questa ipotesi si osserva come sono distribuiti i valori dei residui. Può essere testato utilizzando due metodi,

· Un istogramma che mostra una curva normale sovrapposta e

· Il metodo del grafico di probabilità normale.

Istanze in cui viene applicata la regressione lineare multipla

La regressione lineare multipla è un aspetto molto importante dal punto di vista dell'analista. Ecco alcuni degli esempi in cui il concetto può essere applicabile:

io. Poiché il valore della variabile dipendente è correlato alle variabili indipendenti, viene utilizzata la regressione multipla per prevedere la resa attesa di un raccolto a determinati livelli di precipitazioni, temperature e fertilizzanti.

ii. L'analisi di regressione lineare multipla viene utilizzata anche per prevedere le tendenze e i valori futuri. Ciò è particolarmente utile per prevedere il prezzo dell'oro nei prossimi sei mesi.

iii. In un esempio particolare in cui viene estratta la relazione tra la distanza percorsa da un conducente UBER e l'età del conducente e il numero di anni di esperienza del conducente. In questa regressione, la variabile dipendente è la distanza percorsa dal conducente UBER. Le variabili indipendenti sono l'età del conducente e il numero di anni di esperienza nella guida.

IV. Un altro esempio in cui l'analisi di regressioni multiple viene utilizzata per trovare la relazione tra il GPA di una classe di studenti e il numero di ore di studio e l'altezza degli studenti. La variabile dipendente in questa regressione è il GPA e le variabili indipendenti sono il numero di ore di studio e l'altezza degli studenti.

v. La relazione tra la retribuzione di un gruppo di dipendenti in un'organizzazione e il numero di anni di espatrio e l'età dei dipendenti può essere determinata con un'analisi di regressione. La variabile dipendente per questa regressione è lo stipendio e le variabili indipendenti sono l'esperienza e l'età dei dipendenti.

Leggi anche: 6 tipi di modelli di regressione nell'apprendimento automatico che dovresti conoscere

Regressione lineare multipla in R

Esistono molti modi in cui è possibile eseguire la regressione lineare multipla, ma comunemente viene eseguita tramite un software statistico. Uno dei software più utilizzati è R che è gratuito, potente e facilmente disponibile. Impareremo prima i passaggi per eseguire la regressione con R, seguiti da un esempio di chiara comprensione.

Passaggi per eseguire la regressione multipla in R

1. Raccolta dati: Vengono raccolti i dati da utilizzare nella previsione.
2. Acquisizione dati in R: acquisizione dei dati utilizzando il codice e importazione di un file CSV
3. Verifica della linearità dei dati con R: È importante assicurarsi che esista una relazione lineare tra la variabile dipendente e quella indipendente. Può essere fatto usando grafici a dispersione o il codice in R
4. Applicazione della regressione lineare multipla in R: Utilizzo del codice per applicare la regressione lineare multipla in R per ottenere un insieme di coefficienti.
5. Fare pronostici con R: Alla fine viene determinato un valore previsto.

Implementazione della regressione multipla in R

Capiremo come viene implementato R quando un sondaggio viene condotto in un certo numero di luoghi dai ricercatori di salute pubblica per raccogliere i dati sulla popolazione che fuma, che si reca al lavoro e le persone con malattie cardiache.

Guida passo passo per la regressione lineare multipla in R:

io. Carica il set di dati heart.data ed esegui il codice seguente

lm<-lm(heart.disease ~ ciclismo + fumo, data = heart.data)

Il cuore del set di dati. I dati calcolano l'effetto delle variabili indipendenti ciclismo e fumo sulla variabile dipendente cardiopatia utilizzando 'lm()' (l'equazione per il modello lineare).

ii. Interpretazione dei risultati

utilizzare la funzione summary() per visualizzare i risultati del modello:

sommario(heart.disease.lm)

Questa funzione inserisce i parametri più importanti ottenuti dal modello lineare in una tabella che appare come di seguito:

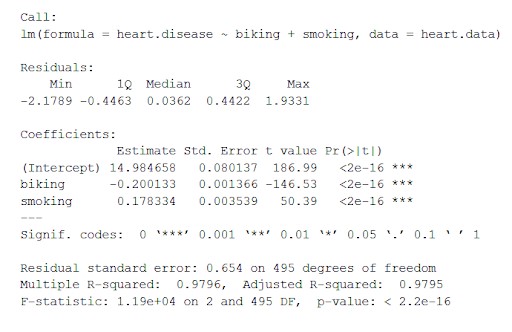
Da questa tabella possiamo dedurre:

• La formula di 'Chiama',
• I residui del modello ("Residui"). Se i residui sono approssimativamente centrati attorno allo zero e con una diffusione simile su entrambi i lati (mediana 0,03 e minimo e massimo -2 e 2), il modello si adatta alle ipotesi di eteroschedasticità.
• I coefficienti di regressione del modello ('Coefficienti').

Riga 1 della tabella dei coefficienti (Intercetta): questa è l'intercetta y dell'equazione di regressione e utilizzata per conoscere l'intercetta stimata per collegare l'equazione di regressione e prevedere i valori delle variabili dipendenti.

malattie cardiache = 15 + (-0,2*in bicicletta) + (0,178*fumo) ± e

Alcuni termini relativi alla regressione multipla

io. Colonna stima : è l'effetto stimato ed è anche chiamato coefficiente di regressione o valore r2. Le stime dicono che per ogni aumento dell'uno per cento di andare in bicicletta al lavoro c'è una diminuzione associata dello 0,2 per cento delle malattie cardiache e per ogni aumento percentuale del fumo c'è un aumento dello 0,17 per cento delle malattie cardiache.

ii. Std.error : Visualizza l'errore standard del preventivo. Questo è un numero che mostra variazioni intorno alle stime del coefficiente di regressione.

iii. t Valore : Visualizza la statistica del test . È un valore t da un t-test a due code .

IV. Pr( > | t | ) : è il valore p che mostra la probabilità di occorrenza del valore t .

Segnalazione dei risultati

Dovremmo includere l'effetto stimato, l'errore di stima standard e il valore p .

Nell'esempio sopra, le relazioni significative tra la frequenza della bicicletta per andare al lavoro e le malattie cardiache e la frequenza del fumo e delle malattie cardiache sono risultate essere p < 0,001.

La frequenza delle malattie cardiache è ridotta dello 0,2% (o ± 0,0014) per ogni aumento dell'1% in bicicletta. La frequenza delle malattie cardiache aumenta dello 0,178% (o ± 0,0035) per ogni aumento dell'1% del fumo.

Rappresentazione grafica dei risultati

Gli effetti di più variabili indipendenti sulla variabile dipendente possono essere mostrati in un grafico. In questo, solo una variabile indipendente può essere tracciata sull'asse x.

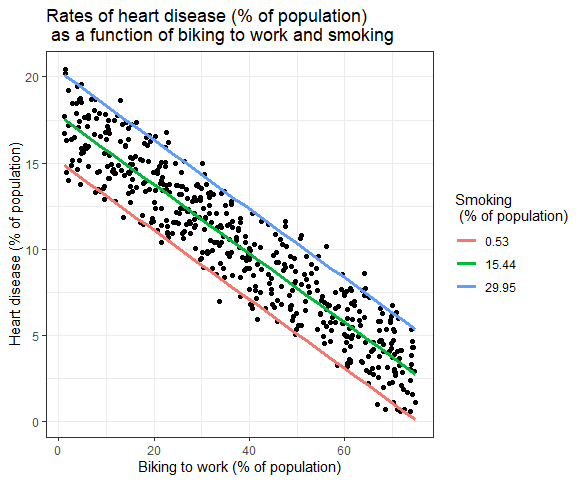
Regressione lineare multipla: rappresentazione grafica

Qui vengono tracciati i valori previsti della variabile dipendente (malattia cardiaca) rispetto ai valori osservati per la percentuale di persone che vanno al lavoro in bicicletta.

Per l'effetto del fumo sulla variabile indipendente, vengono calcolati i valori previsti, mantenendo costante il fumo ai tassi di fumo minimo, medio e massimo.

Leggi anche: Regressione lineare vs. Regressione logistica: differenza tra regressione lineare e regressione logistica

Parole finali

Questo segna la fine di questo post sul blog. Abbiamo fatto il meglio dei nostri sforzi per spiegarti il ​​concetto di regressione lineare multipla e come viene implementata la regressione multipla in R per facilitare l'analisi della previsione.

Se desideri sostenere il tuo viaggio nella scienza dei dati e apprendere più concetti di R e molte altre lingue per rafforzare la tua carriera, unisciti a upGrad . Offriamo il programma di certificazione avanzato in Data Science , appositamente progettato per i professionisti che lavorano e include oltre 300 ore di apprendimento con tutoraggio continuo.