Regresie liniară multiplă în R [cu grafice și exemple]

În calitate de cercetător al datelor, vi se cere frecvent să faceți analize predictive în multe proiecte. O analiză este o abordare statistică pentru stabilirea unei relații între o variabilă dependentă cu un set de variabile independente. Întregul concept poate fi numit regresie liniară, care este în principiu de două tipuri: regresie liniară simplă și multiplă.

R este unul dintre cele mai importante limbaje în ceea ce privește știința și analiza datelor, la fel și regresia liniară multiplă în R deține valoare. Acesta descrie scenariul în care o singură variabilă de răspuns Y depinde liniar de mai multe variabile predictoare.

Ce este o regresie liniară?

Modelele de regresie liniară sunt utilizate pentru a arăta sau prezice relația dintre a dependentă și o variabilă independentă. Când există două sau mai multe variabile independente utilizate în analiza de regresie, modelul nu este pur și simplu liniar, ci un model de regresie multiplă.

Regresia liniară simplă este utilizată pentru a prezice valoarea unei variabile prin utilizarea altei variabile. O linie dreaptă reprezintă relația dintre cele două variabile cu regresie liniară.

Există o relație liniară între o variabilă dependentă cu două sau mai multe variabile independente în regresie multiplă. Relația poate fi, de asemenea, neliniară, iar variabilele dependente și independente nu vor urma o linie dreaptă.

Reprezentare picturală a predicțiilor modelului de regresie liniară multiplă

Regresia liniară și neliniară sunt utilizate pentru a urmări un răspuns folosind două sau mai multe variabile. Regresia neliniară este creată din ipoteze din încercare și eroare și este relativ dificil de executat.

Ce este regresia liniară multiplă?

Regresia liniară multiplă este o tehnică de analiză statistică utilizată pentru a prezice rezultatul unei variabile pe baza a două sau mai multe variabile. Este o extensie a regresiei liniare și este cunoscută și ca regresie multiplă. Variabila care trebuie prezisă este variabila dependentă, iar variabilele utilizate pentru a prezice valoarea variabilei dependente sunt cunoscute ca variabile independente sau explicative.

Regresia liniară multiplă le permite analiștilor să determine variația modelului și contribuția relativă a fiecărei variabile independente. Regresia multiplă este de două tipuri, regresia liniară și regresia neliniară.

Formula de regresie multiplă

Regresia multiplă cu trei variabile predictoare (x) care predică variabila y este exprimată ca următoarea ecuație:

y = z0 + z1*x1 + z2*x2 + z3*x3

Valorile „z” reprezintă ponderile de regresie și sunt coeficienții beta . Ele sunt asocierea dintre variabila predictor și rezultat.

• yi este o variabilă dependentă sau prezisă
• z0 este intersecția cu y, adică valoarea lui y când x1 și x2 sunt 0
• z1 și z2 sunt coeficienții de regresie reprezentând modificarea în y legată de o modificare de o unitate a x1 și , respectiv, x2 .

Ipoteze ale regresiei liniare multiple

Am cunoscut brief-ul despre regresia multiplă și formula de bază. Cu toate acestea, există câteva ipoteze pe care regresia liniară multiplă se bazează pe detaliat, după cum urmează:

i. Relația dintre variabile dependente și independente

Variabila dependentă se raportează liniar cu fiecare variabilă independentă. Pentru a verifica relațiile liniare, este creat un grafic de dispersie și este observat pentru liniaritate. Dacă relația scatterplot este neliniară, atunci se efectuează o regresie neliniară sau datele sunt transferate folosind un software statistic.

ii. Variabilele independente nu sunt prea corelate

Datele nu ar trebui să afișeze multicoliniaritate, ceea ce se întâmplă în cazul în care variabilele independente sunt foarte corelate între ele. Acest lucru va crea probleme în extragerea variabilei specifice care contribuie la variația variabilei dependente.

iii. Varianta reziduala este constanta

Regresia liniară multiplă presupune că eroarea variabilelor rămase este similară în fiecare punct al modelului liniar. Acest lucru este cunoscut sub numele de homoscedasticitate. Când analiza datelor este efectuată, reziduurile standard față de valorile prezise sunt reprezentate grafic pentru a determina dacă punctele sunt distribuite corect între valorile variabilelor independente.

iv. Independența de observare

Observațiile ar trebui să fie una ale altora, iar valorile reziduale ar trebui să fie independente. Statistica Durbin Watson funcționează cel mai bine pentru asta.

Metoda arată valori de la 0 la 4, unde o valoare între 0 și 2 arată autocorelație pozitivă, iar de la 2 la 4 arată autocorelație negativă. Punctul de mijloc, o valoare de 2, arată că nu există autocorelație.

v. Normalitate multivariată

Normalitatea multivariată se întâmplă cu reziduuri distribuite normal. Pentru această ipoteză, se observă modul în care sunt distribuite valorile reziduurilor. Poate fi testat folosind două metode,

· O histogramă care arată o curbă normală suprapusă și

· Metoda Normal Probability Plot.

Instanțe în care se aplică regresia liniară multiplă

Regresia liniară multiplă este un aspect foarte important din punctul de vedere al analistului. Iată câteva dintre exemplele în care conceptul poate fi aplicabil:

i. Deoarece valoarea variabilei dependente este corelată cu variabilele independente, regresia multiplă este utilizată pentru a prezice randamentul așteptat al unei culturi la un anumit nivel de precipitații, temperatură și îngrășământ.

ii. Analiza de regresie liniară multiplă este, de asemenea, utilizată pentru a prezice tendințele și valorile viitoare. Acest lucru este deosebit de util pentru a prezice prețul aurului în următoarele șase luni.

iii. Într-un exemplu special în care este eliminată relația dintre distanța parcursă de un șofer UBER și vârsta șoferului și numărul de ani de experiență a șoferului. În această regresie, variabila dependentă este distanța parcursă de șoferul UBER. Variabilele independente sunt vârsta șoferului și numărul de ani de experiență în conducere.

iv. Un alt exemplu în care analiza regresiilor multiple este utilizată pentru a găsi relația dintre GPA-ul unei clase de elevi și numărul de ore pe care le studiază și înălțimea elevilor. Variabila dependentă din această regresie este GPA, iar variabilele independente sunt numărul de ore de studiu și înălțimile studenților.

v. Relația dintre salariul unui grup de angajați dintr-o organizație și numărul de ani de experiență în organizație, vârsta angajaților poate fi determinată printr-o analiză de regresie. Variabila dependentă pentru această regresie este salariul, iar variabilele independente sunt experiența și vârsta angajaților.

Citește și: 6 tipuri de modele de regresie în învățarea automată despre care ar trebui să știi

Regresia liniară multiplă în R

Există multe moduri în care regresia liniară multiplă poate fi executată, dar se face de obicei prin intermediul unui software statistic. Unul dintre cele mai utilizate programe software este R, care este gratuit, puternic și ușor disponibil. Vom învăța mai întâi pașii pentru a efectua regresia cu R, urmați de un exemplu de înțelegere clară.

Pași pentru a efectua regresia multiplă în R

1. Colectare de date: Sunt colectate datele care vor fi utilizate în predicție.
2. Capturarea datelor în R: Capturarea datelor folosind codul și importul unui fișier CSV
3. Verificarea liniarității datelor cu R: Este important să vă asigurați că există o relație liniară între variabila dependentă și variabila independentă. Se poate face folosind diagrame de dispersie sau codul din R
4. Aplicarea regresiei liniare multiple în R: Utilizarea codului pentru a aplica regresia liniară multiplă în R pentru a obține un set de coeficienți.
5. Efectuarea de predicții cu R: O valoare estimată este determinată la sfârșit.

Implementarea regresiei multiple în R

Vom înțelege cum este implementat R atunci când un sondaj este efectuat într-un anumit număr de locuri de către cercetătorii de sănătate publică pentru a culege date despre populația care fumează, care călătorește la locul de muncă și persoanele cu o boală de inimă.

Ghid pas cu pas pentru regresia liniară multiplă în R:

i. Încărcați setul de date heart.data și rulați următorul cod

lm<-lm(heart.disease ~ ciclism + fumat, data = heart.data)

Inima setului de date. Datele calculează efectul variabilelor independente ciclism și fumat asupra variabilei dependente boli cardiace folosind „lm()” (ecuația pentru modelul liniar).

ii. Interpretarea rezultatelor

utilizați funcția summary() pentru a vizualiza rezultatele modelului:

rezumat(heart.disease.lm)

Această funcție plasează cei mai importanți parametri obținuți din modelul liniar într-un tabel care arată mai jos:

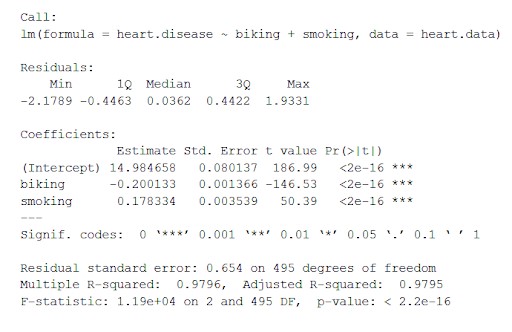
Din acest tabel putem deduce:

• Formula „Apel”,
• Reziduurile modelului („Reziduuri”). Dacă reziduurile sunt aproximativ centrate în jurul zero și cu o răspândire similară pe ambele părți (mediana 0,03 și min și max -2 și 2), atunci modelul se potrivește ipotezelor de heteroscedasticitate.
• Coeficienții de regresie ai modelului („Coeficienți”).

Rândul 1 al tabelului de coeficienți (Interceptare): Aceasta este intersecția cu y a ecuației de regresie și folosită pentru a cunoaște intersecția estimată pentru a introduce ecuația de regresie și a prezice valorile variabilelor dependente.

boli de inimă = 15 + (-0,2*ciclism) + (0,178*fumat) ± e

Unii termeni legați de regresia multiplă

i. Coloana Estimare : Este efectul estimat și se mai numește și coeficient de regresie sau valoarea r2. Estimările spun că pentru fiecare creștere de 1% a mersului cu bicicleta la locul de muncă există o scădere asociată cu 0,2% a bolilor de inimă, iar pentru fiecare creștere procentuală a fumatului există o creștere de 0,17% a bolilor de inimă.

ii. Std.error : Afișează eroarea standard a devizului. Acesta este un număr care arată variația în jurul estimărilor coeficientului de regresie.

iii. t Valoare : Afişează statistica testului . Este o valoare t dintr-un test t cu două fețe .

iv. Pr( > | t | ) : este valoarea p care arată probabilitatea de apariție a valorii t .

Raportarea rezultatelor

Ar trebui să includem efectul estimat, eroarea standard de estimare și valoarea p .

În exemplul de mai sus, relațiile semnificative dintre frecvența mersului cu bicicleta la locul de muncă și bolile de inimă și frecvența fumatului și bolile cardiace s-au dovedit a fi p < 0,001.

Frecvența bolilor de inimă este scăzută cu 0,2% (sau ± 0,0014) pentru fiecare creștere de 1% a ciclismului. Frecvența bolilor de inimă crește cu 0,178% (sau ± 0,0035) pentru fiecare creștere cu 1% a fumatului.

Reprezentarea grafică a constatărilor

Efectele mai multor variabile independente asupra variabilei dependente pot fi prezentate într-un grafic. În aceasta, doar o variabilă independentă poate fi reprezentată grafic pe axa x.

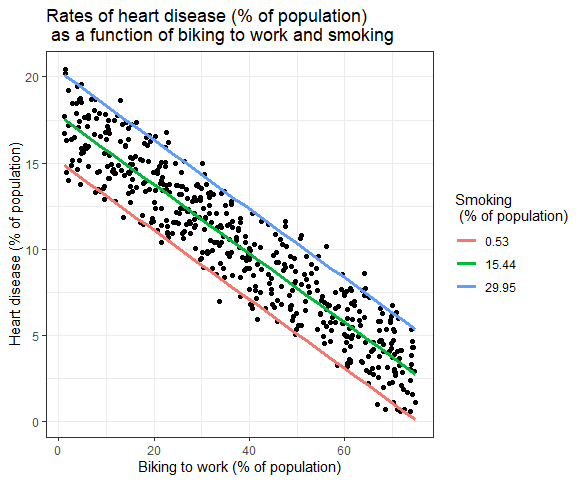
Regresie liniară multiplă: reprezentare grafică

Aici, sunt reprezentate grafic valorile prezise ale variabilei dependente (boala cardiacă) în cadrul valorilor observate pentru procentul de oameni care merg cu bicicleta la serviciu.

Pentru efectul fumatului asupra variabilei independente, se calculează valorile prezise, ​​menținând constant fumatul la ratele minime, medii și maxime ale fumatului.

Citește și: Regresia liniară vs. Regresia logistică: diferența dintre regresia liniară și regresia logistică

Cuvinte finale

Acesta marchează sfârșitul acestei postări pe blog. Am încercat tot posibilul pentru a vă explica conceptul de regresie liniară multiplă și modul în care regresia multiplă din R este implementată pentru a ușura analiza predicției.

Dacă doriți să vă susțineți călătoria în domeniul științei datelor și să aflați mai multe concepte de R și multe alte limbi pentru a vă consolida cariera, alăturați -vă upGrad . Oferim programul de certificare avansată în știința datelor, care este special conceput pentru profesioniștii care lucrează și include peste 300 de ore de învățare cu mentorat continuu.